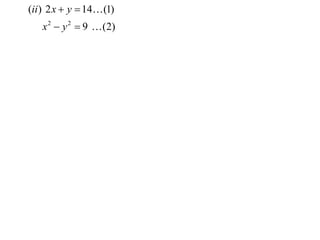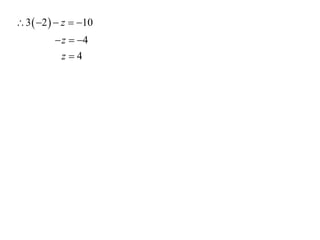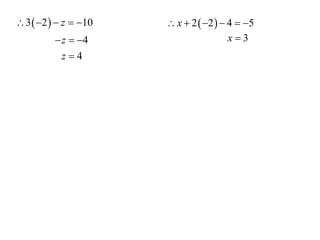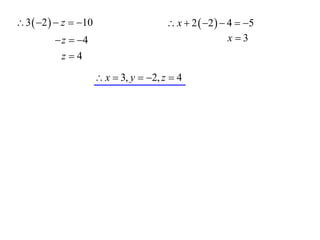The document describes how to solve simultaneous equations using three steps: 1) eliminate a variable from the equations, 2) solve for the remaining variable, and 3) substitute back to find the eliminated variable. It provides an example showing these steps to solve two simultaneous equations for x and y. It then shows another example involving eliminating variables to create two new equations that can be solved simultaneously for y and z. The key points are eliminating variables to reduce the equations, then solving the reduced equations to find the values of the variables.

1. Simultaneous Equations

2. Simultaneous Equations
1) Eliminate a variable

3. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable

4. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable
3) Substitute to find the eliminated variable

5. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable
3) Substitute to find the eliminated variable
e.g. (i ) 2 x  3 y  21 (1)
5 x  2 y  3  (2)

6. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable
3) Substitute to find the eliminated variable
e.g. (i ) 2 x  3 y  21 (1)
5 x  2 y  3  (2)
Multiply (1) by 2 and (2) by 3

7. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable
3) Substitute to find the eliminated variable
e.g. (i ) 2 x  3 y  21 (1)
5 x  2 y  3  (2)
Multiply (1) by 2 and (2) by 3
4 x  6 y  42
15 x  6 y  9

8. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable
3) Substitute to find the eliminated variable
e.g. (i ) 2 x  3 y  21 (1)
5 x  2 y  3  (2)
Multiply (1) by 2 and (2) by 3
4 x  6 y  42
15 x  6 y  9
11x =  33

9. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable
3) Substitute to find the eliminated variable
e.g. (i ) 2 x  3 y  21 (1)
5 x  2 y  3  (2)
Multiply (1) by 2 and (2) by 3
4 x  6 y  42
15 x  6 y  9
11x =  33
x = 3

10. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable
3) Substitute to find the eliminated variable
e.g. (i ) 2 x  3 y  21 (1)
5 x  2 y  3  (2)
Multiply (1) by 2 and (2) by 3
4 x  6 y  42
15 x  6 y  9
11x =  33  2  3  3 y  21
x = 3 3 y  27
y9

11. Simultaneous Equations
1) Eliminate a variable
2) Solve for the other variable
3) Substitute to find the eliminated variable
e.g. (i ) 2 x  3 y  21 (1)
5 x  2 y  3  (2)
Multiply (1) by 2 and (2) by 3
4 x  6 y  42
15 x  6 y  9
11x =  33  2  3  3 y  21
x = 3 3 y  27
y9
 x  3, y  9

12. (ii ) 2 x  y  14 (1)
x 2  y 2  9  (2)

13. (ii ) 2 x  y  14 (1)
x 2  y 2  9  (2)
Make y the subject in (1)
y  14  2 x

14. (ii ) 2 x  y  14 (1)
x 2  y 2  9  (2)
Make y the subject in (1)
y  14  2 x
Substitute into (2)
x 2  14  2 x   9
2

15. (ii ) 2 x  y  14 (1)
x 2  y 2  9  (2)
Make y the subject in (1)
y  14  2 x
Substitute into (2)
x 2  14  2 x   9
2
x 2  196  56 x  4 x 2  9
3 x 2  56 x  205  0

16. (ii ) 2 x  y  14 (1)
x 2  y 2  9  (2)
Make y the subject in (1)
y  14  2 x
Substitute into (2)
x 2  14  2 x   9
2
x 2  196  56 x  4 x 2  9
3 x 2  56 x  205  0
 3x  41 x  5   0
41
x  5 or x 
3

17. (ii ) 2 x  y  14 (1)
x 2  y 2  9  (2)
Make y the subject in (1)
y  14  2 x
Substitute into (2)
x 2  14  2 x   9
2
x 2  196  56 x  4 x 2  9
3 x 2  56 x  205  0
 3x  41 x  5   0
41
x  5 or x 
3
 41    14
2  5   y  14 or 2   y
3
40
y  4 or y  
3

18. (ii ) 2 x  y  14 (1)
x 2  y 2  9  (2)
Make y the subject in (1)
y  14  2 x
Substitute into (2)
x 2  14  2 x   9
2
x 2  196  56 x  4 x 2  9
3 x 2  56 x  205  0
 3x  41 x  5   0
41
x  5 or x 
3
 41    14
2  5   y  14 or 2   y
3
41 40
40  x  5, y  4 or x  , y  
y  4 or y   3 3
3

19. (iii ) x  2 y  z  5  (1)
2 x  3 y  4 z  28  (2) any time you have the same number of
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values

20. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both

21. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both
Multiply (1) by 2
2 x  4 y  2 z  10
2 x  3 y  4 z  28

22. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both
Multiply (1) by 2
2 x  4 y  2 z  10
2 x  3 y  4 z  28
7 y  6 z  38

23. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both
Multiply (1) by 2 Multiply (1) by 4
2 x  4 y  2 z  10 4 x  8 y  4 z  20
2 x  3 y  4 z  28 4 x  5 y  3 z  10
7 y  6 z  38

24. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both
Multiply (1) by 2 Multiply (1) by 4
2 x  4 y  2 z  10 4 x  8 y  4 z  20
2 x  3 y  4 z  28 4 x  5 y  3 z  10
7 y  6 z  38 3 y  z  10

25. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both
Multiply (1) by 2 Multiply (1) by 4
2 x  4 y  2 z  10 4 x  8 y  4 z  20
2 x  3 y  4 z  28 4 x  5 y  3 z  10
7 y  6 z  38 3 y  z  10
Solve these new equations simultaneously

26. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both
Multiply (1) by 2 Multiply (1) by 4
2 x  4 y  2 z  10 4 x  8 y  4 z  20
2 x  3 y  4 z  28 4 x  5 y  3 z  10
7 y  6 z  38 3 y  z  10
Solve these new equations simultaneously
7 y  6 z  38
18 y  6 z  60

27. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both
Multiply (1) by 2 Multiply (1) by 4
2 x  4 y  2 z  10 4 x  8 y  4 z  20
2 x  3 y  4 z  28 4 x  5 y  3 z  10
7 y  6 z  38 3 y  z  10
Solve these new equations simultaneously
7 y  6 z  38
18 y  6 z  60

28. (iii ) x  2 y  z  5  (1)
any time you have the same number of
2 x  3 y  4 z  28  (2)
pronumerals as equations it should
4 x  5 y  3 z  10 (3) be possible to find their values
Create two pairs of two equations and
eliminate the same variable from both
Multiply (1) by 2 Multiply (1) by 4
2 x  4 y  2 z  10 4 x  8 y  4 z  20
2 x  3 y  4 z  28 4 x  5 y  3 z  10
7 y  6 z  38 3 y  z  10
Solve these new equations simultaneously
7 y  6 z  38
18 y  6 z  60
11 y  22
y  2

29.  3  2   z  10
 z  4
z4

30.  3  2   z  10  x  2  2   4  5
 z  4 x3
z4

31.  3  2   z  10  x  2  2   4  5
 z  4 x3
z4
 x  3, y  2, z  4

32.  3  2   z  10  x  2  2   4  5
 z  4 x3
z4
 x  3, y  2, z  4
Exercise 1H; 1bg, 2cfil, 3aceg, 4aegh, 5a,
6ace, 7ad, 8*b, 9***