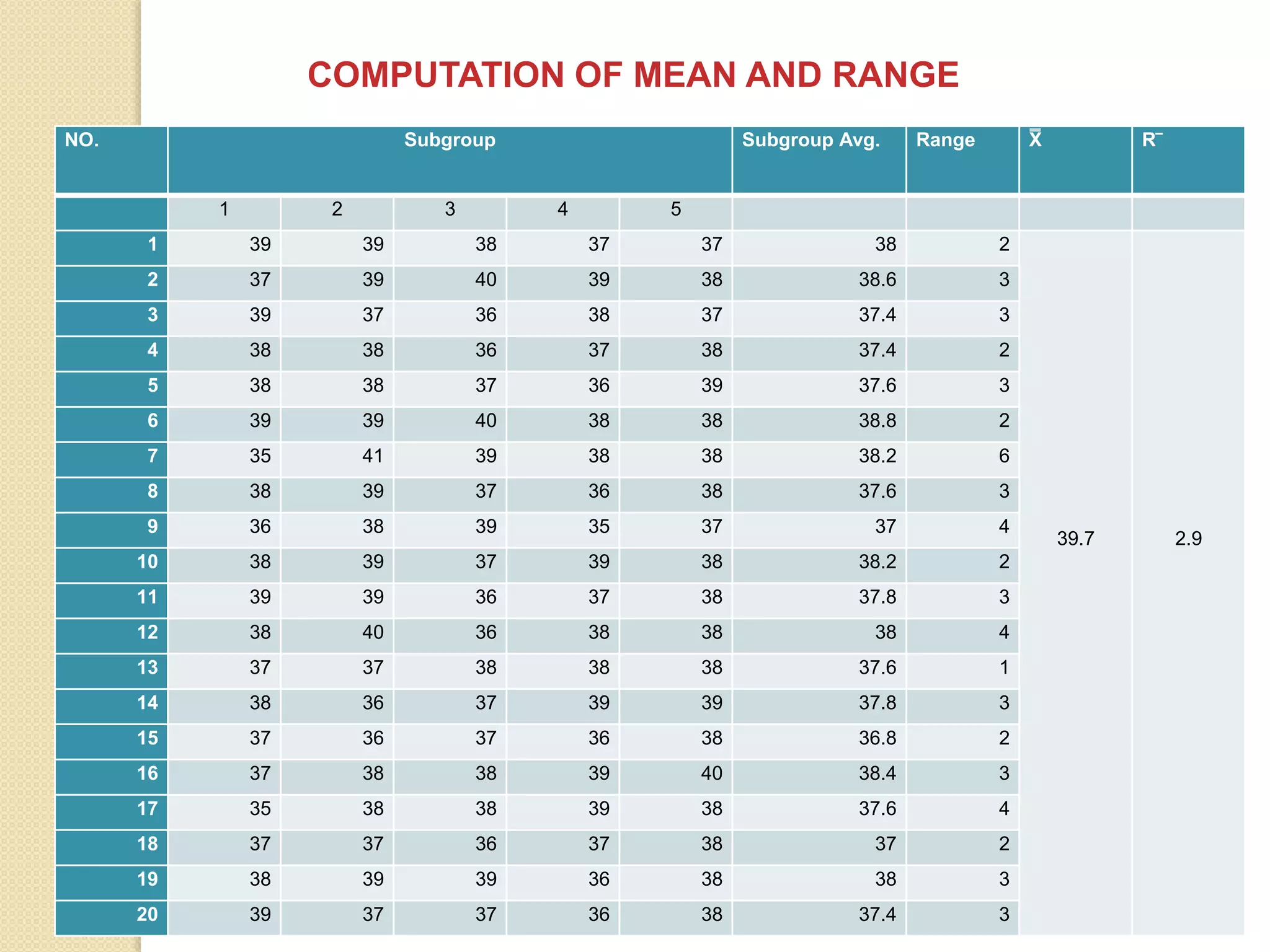
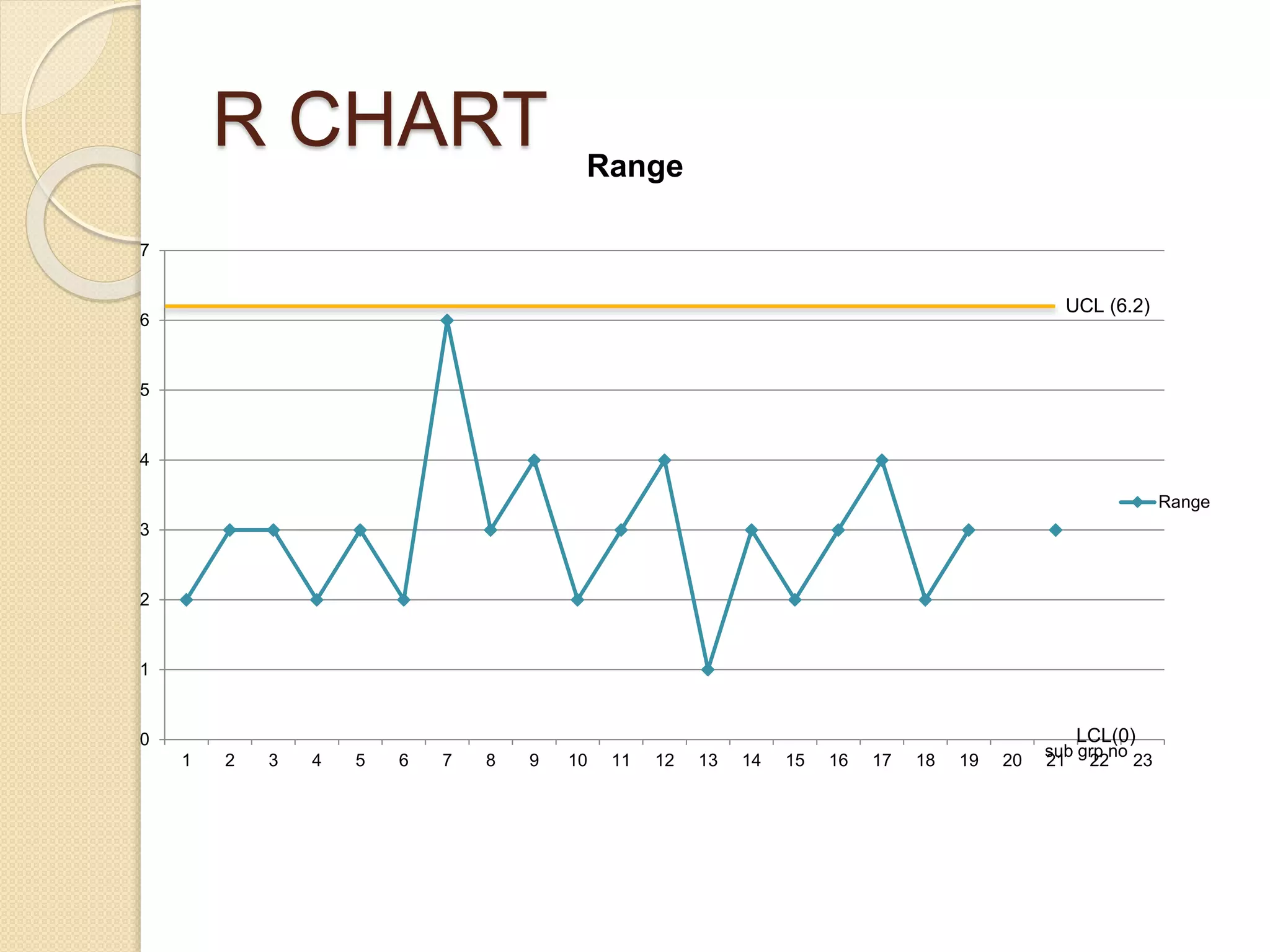
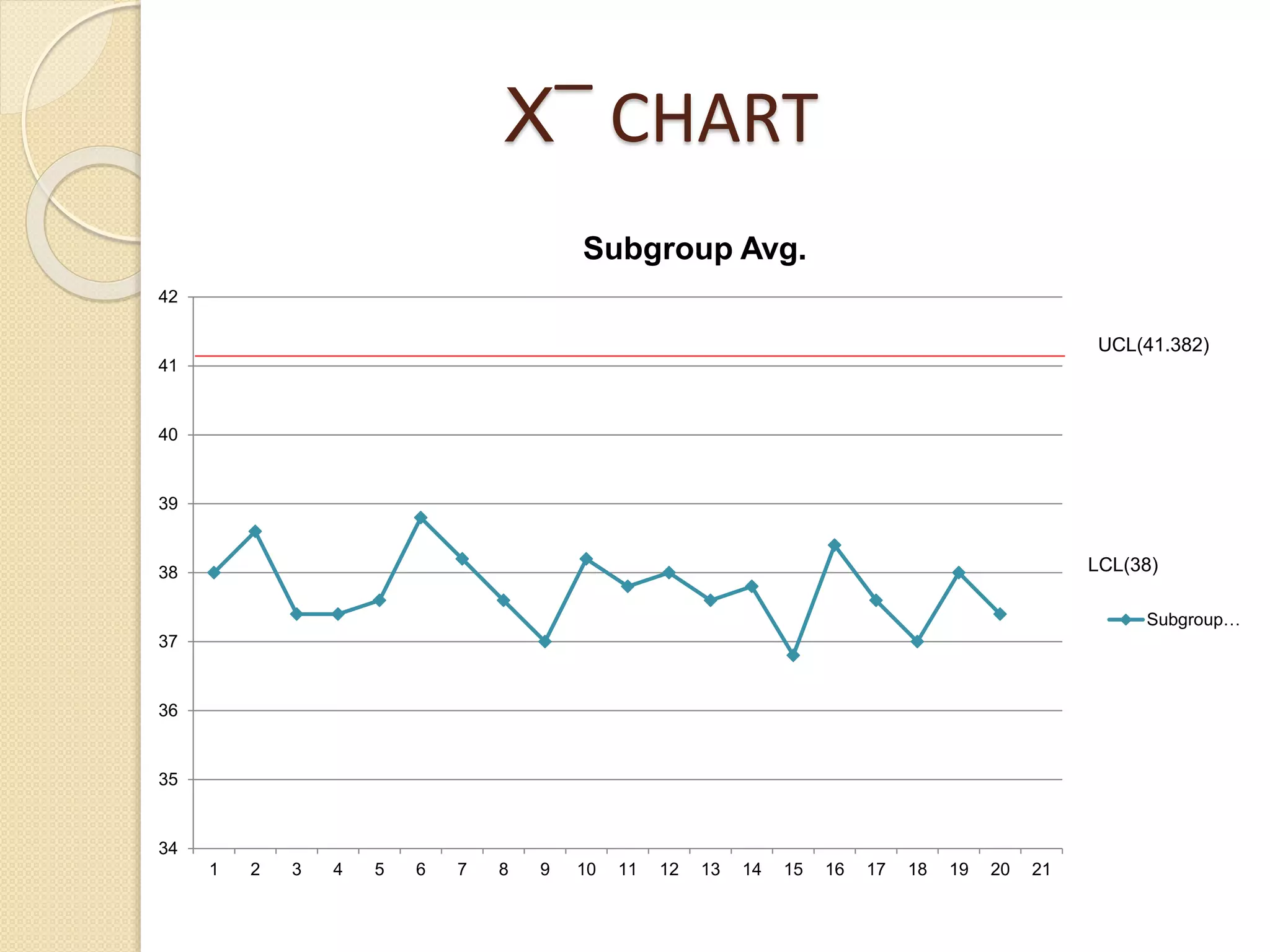
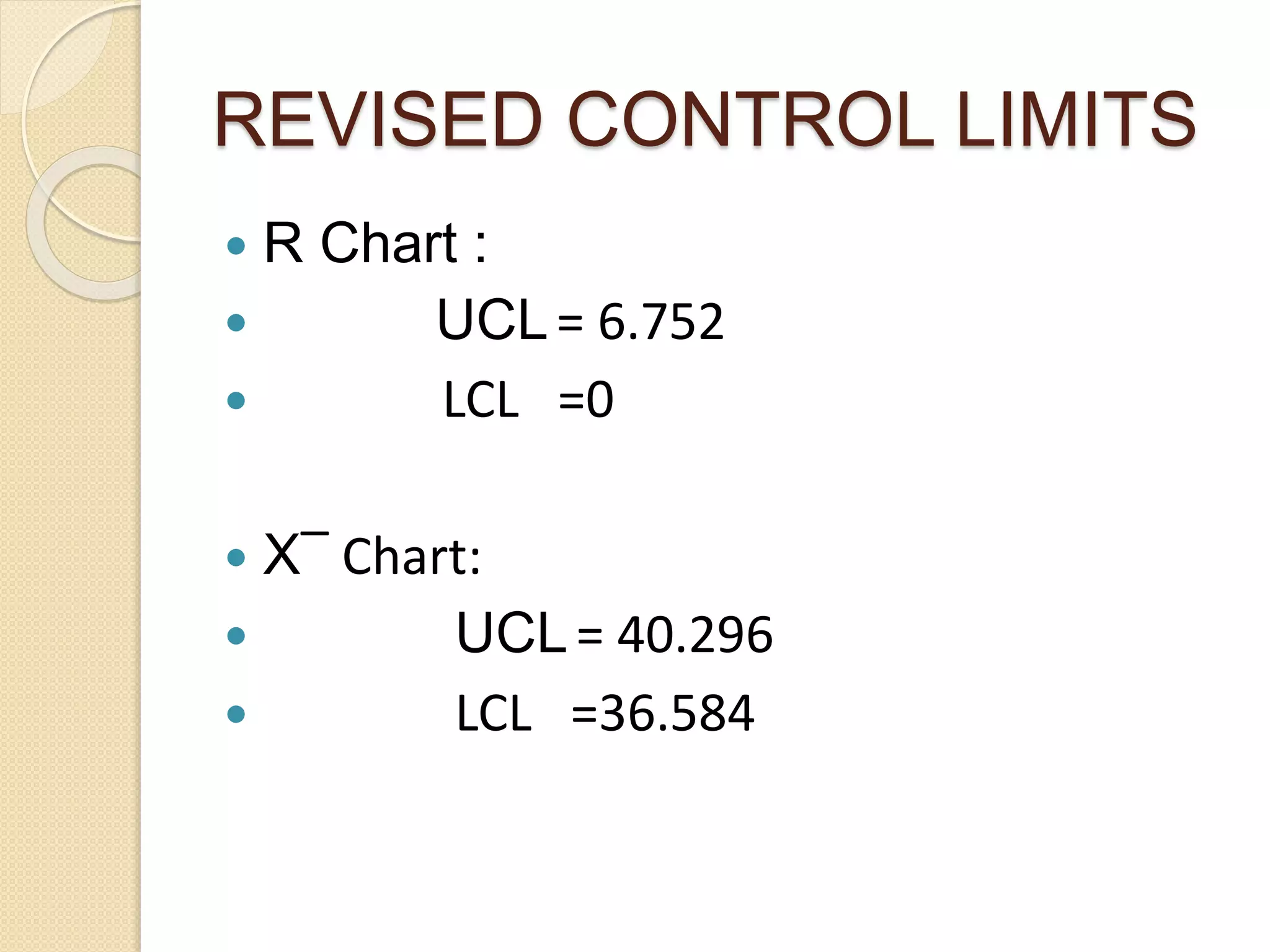
The document discusses the construction and application of x̅ and R control charts for monitoring process average and variation in quality control. It details step-by-step procedures for calculating sample averages and ranges, constructing charts, and analyzing a case study involving 100 work pieces to determine process control limits. The final findings indicate that the process is under control, with all points lying within revised control limits.

1. SEMINAR ON
X‾ AND R CHARTS
1.AKHIL KRISHNAN G
2.MADHUSOODHANAN
3.MOHAMMED SHAFEEQ P K
4.VARUN RAJ M
5.VISHNU S

2. INTRODUCTION
 X‾ -R Chart maximum utilization of information
available from data & provide detailed
information in process average & variation for
control of individual dimensions.
 Samples(subgroup size) are drawn at intervals
and measures are taken.

3. Control charts for X‾ & R are
constructed for
a) A process is behaving normally.
b) No assignable cause are present.
c) Ensure product quality level.

4. The chart is advantageous in the
following situations
 The sample size is relatively small (say, n
≤ 10)— x‾and s charts are typically used
for larger sample sizes)
 The sample size is constant
 Humans must perform the calculations for
the chart

5. Construction of X‾ & R Chart.
1. Begin taking samples and place the numbers on the
chart in the order they are taken.
2. Calculate the average of each sample.
3. Divide sum by the total number of samples taken for
any particular time.
4. Calculate the overall average by adding on the figure
in the average X‾ row and dividing that total by the
number of readings in the row.
5. Find the range by subtracting the smaller number from
the larger number.
6. Calculate the average range R‾ by the summing all
range entries and dividing by the number of entries.

6. Construction of X‾ & R Chart.
7. To calculate the graph scales begin by first
finding the larger and smallest average X‾ and
the largest and smallest range.
8. Plot the data using the average data for the top
graph and the range data for the lower graph
and connect the dots forming a line for the
averages and another for ranges.
9. Draw heavy line at those points from one end
of each graph to the other and label them.

7. CASE STUDY
 Here we are considering 100 finished
work pieces from fitting workshop for
our analysis
 Width of each work piece was
measured and as taken as desired
dimension
 Study leads to the following results

8. COMPUTATION OF MEAN AND RANGE
NO. Subgroup Subgroup Avg. Range X̿ R‾
1 2 3 4 5
1 39 39 38 37 37 38 2
39.7 2.9
2 37 39 40 39 38 38.6 3
3 39 37 36 38 37 37.4 3
4 38 38 36 37 38 37.4 2
5 38 38 37 36 39 37.6 3
6 39 39 40 38 38 38.8 2
7 35 41 39 38 38 38.2 6
8 38 39 37 36 38 37.6 3
9 36 38 39 35 37 37 4
10 38 39 37 39 38 38.2 2
11 39 39 36 37 38 37.8 3
12 38 40 36 38 38 38 4
13 37 37 38 38 38 37.6 1
14 38 36 37 39 39 37.8 3
15 37 36 37 36 38 36.8 2
16 37 38 38 39 40 38.4 3
17 35 38 38 39 38 37.6 4
18 37 37 36 37 38 37 2
19 38 39 39 36 38 38 3
20 39 37 37 36 38 37.4 3

9. Calculations
 X̿=(X₁‾+X₂‾+----+X₂₀‾)/20 = 39.7
 R‾=(R₁+R₂+------+R₂₀)/20 = 2.9
 For subgroup size, n=5
A₂=0.58
D₃=0
D₄=2.11
D₂=2.326

10. Control limits
For X‾ chart
 UCL= X̿ +A₂R‾ =41.382
 LCL= X̿ -A₂R‾ =38.018
For R chart
• UCL=D₄R‾ =6.119
• LCL=D₃R‾ =0

11. R CHART
7
6
5
4
3
2
1
0
Range
UCL (6.2)
LCL(0)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
Range
sub grp no

12. X‾ CHART
42
41
40
39
38
37
36
35
34
Subgroup Avg.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
UCL(41.382)
LCL(38)
Subgroup…

13.  All the values of ranges are lying
between UCL and LCL of R chart
 In X‾ chart some values are out of
control
 So we have to eliminate those groups and
calculate revised control limits

14. REVISED CONTROL LIMITS
 R Chart :
 UCL= 6.752
 LCL =0
 X‾ Chart:
 UCL= 40.296
 LCL =36.584

15. SOME COMMENTS
 Now all the points in both charts are
under control limits the process is
seems to be under control
 Means only chance causes of
variations are present in the process
 Now we can calculate process
average, upper natural limit, lower
natural limit, etc to comment about the
process control

16.  X‾’= Process average= X̿(revised)=38.44
 σ‾=R‾(revised)/D2= 1.375
 Process Capability=6σ‾=8.25
 UNL=X‾’+3σ‾=42.565
 LNL=X‾’-3σ‾=34.315
 Here 6σ‾=UNL-LNL. The process is under
strict control
 Now these limits can use for future
references

17.  THANKYOU