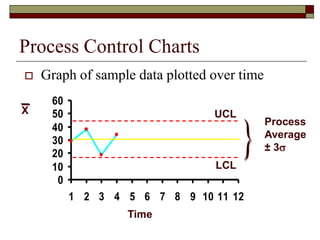
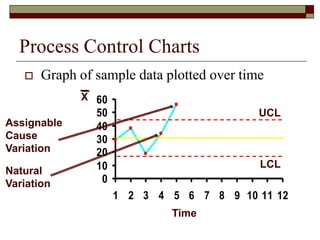
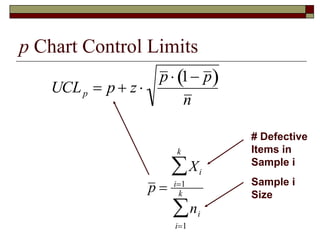
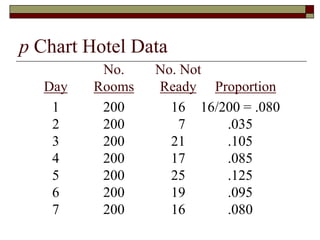
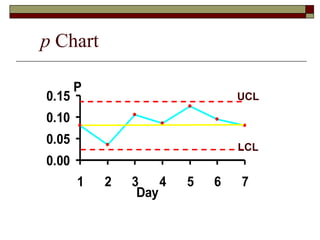
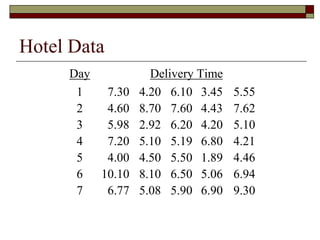
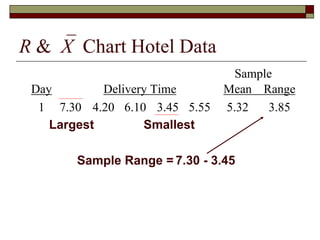
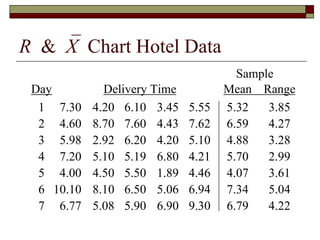
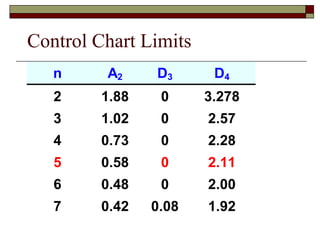
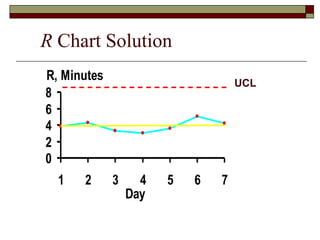
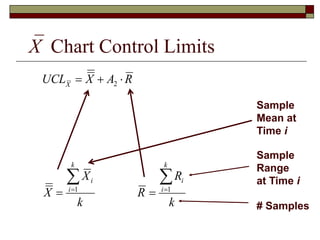
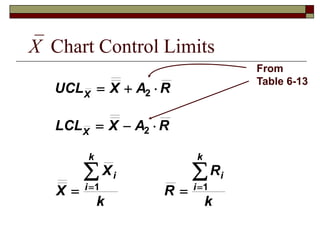
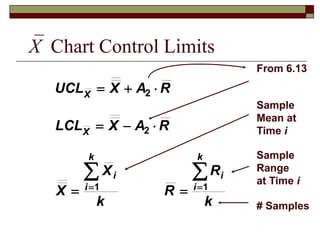
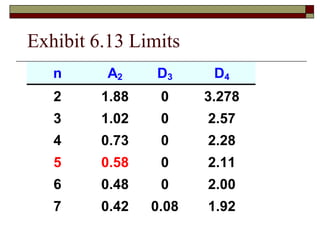
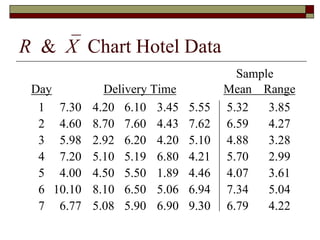
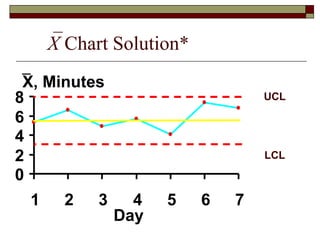
This document discusses statistical process control and control charts. It defines the goals of control charts as collecting and visually presenting data to see when trends or out-of-control points occur. Process control charts graph sample data over time and show the process average and upper and lower control limits. Attribute control charts indicate whether points are in or out of tolerance, while variables charts measure attributes like length, weight or temperature over time. Examples are provided to illustrate p-charts, R-charts and X-bar charts using hotel luggage delivery time data.

1. Statistical Process Control
Managing for Quality
DR. WAQARUDDIN SIDDIQUI
FMSR, DBA
ALIGARH MUSLIM UNIVERSITY

2. Goal of Control Charts
 collect and present data visually
 allow us to see when trend appears
 see when “out of control” point occurs

3. Process Control Charts
 Graph of sample data plotted over time
60
50
40
30
20
10
0
UCL
LCL
1 2 3 4 5 6 7 8 9 10 11 12
Process
Average
± 3
Time
X

4. Process Control Charts
 Graph of sample data plotted over time
60
50
40
30
20
10
0
1 2 3 4 5 6 7 8 9 10 11 12
Assignable
Cause
Variation
Natural
Variation
UCL
LCL
Time
X

5. Definitions of Out of Control
1. No points outside control limits
2. Same number above & below center line
3. Points seem to fall randomly above and
below center line
4. Most are near the center line, only a few are
close to control limits
1. 8 Consecutive pts on one side of centerline
2. 2 of 3 points in outer third
3. 4 of 5 in outer two-thirds region

6. Attributes vs. Variables
Attributes:
 Good / bad, works / doesn’t
 count % bad (P chart)
 count # defects / item (C chart)
Variables:
 measure length, weight, temperature (x-bar
chart)
 measure variability in length (R chart)

7. Attribute Control Charts
 Tell us whether points in tolerance or not
 p chart: percentage with given characteristic
(usually whether defective or not)
 np chart: number of units with characteristic
 c chart: count # of occurrences in a fixed area of
opportunity (defects per car)
 u chart: # of events in a changeable area of
opportunity (sq. yards of paper drawn from a
machine)

8. p Chart Control Limits
# Defective
Items in
Sample i
Sample i
Size
UCLp  p  z 
p  1 p
n
p 
Xi
k

i1
ni
k

i1

9. p Chart Control Limits
z = 2 for
95.5% limits;
z = 3 for
99.7% limits
# Defective
Items in
Sample i
Sample i
Size
# Samples
 
n
p p
UCL p z p
 
  
1
p 
Xi
k

i1
ni
k

i1
n 
ni
k

i1
k

10. p Chart Control Limits
z = 2 for
95.5% limits;
z = 3 for
99.7% limits
# Defective
Items in
Sample i
# Samples
Sample i
Size
 
n
p p
UCL p z p
 
  
1
 
n
p p
LCL p z p
 
  
1
n 
ni
k

i1
k
p 
Xi
k

i1
ni
k

i1

11. p Chart Example
You’re manager of a 500-
room hotel. You want to
achieve the highest level
of service. For 7 days,
you collect data on the
readiness of 200 rooms. Is
the process in control (use
z = 3)?
© 1995 Corel Corp.

12. p Chart Hotel Data
No. No. Not
Day Rooms Ready Proportion
1 200 16 16/200 = .080
2 200 7 .035
3 200 21 .105
4 200 17 .085
5 200 25 .125
6 200 19 .095
7 200 16 .080

13. p Chart Control Limits
n 
ni
k

i1
k

1400
7
 200

14. p Chart Control Limits
16 + 7 +...+ 16

p 
Xi
k

i1
ni
k

i1

121
1400
 0.0864
n 
ni
k

i1
k

1400
7
 200

15. p Chart Solution
16 + 7 +...+ 16

p 
Xi
k

i1
ni
k

i1

121
1400
 0.0864
n 
ni
k

i1
k

1400
7
 200
p  z 
p  1 p 
n
 0.0864  3
0.0864  1 0.0864 
200

16. p Chart Solution
16 + 7 +...+ 16
k

p  z 
p  1 p 
n
p 
k

i1
k

 0.0864  3
Xi
ni
i1

121
1400
 0.0864
0.0864  1 0.0864 
200

 0.0864  3*0.01984  0.0864  0.01984
 0.1460, and 0.0268
n 
ni
i1
k

1400
7
 200

17. 0.15
0.10
0.05
0.00
P
1 2 3 4 5 6 7
Day
p Chart
UCL
LCL

18. R Chart
 Type of variables control chart
 Interval or ratio scaled numerical data
 Shows sample ranges over time
 Difference between smallest & largest values
in inspection sample
 Monitors variability in process
 Example: Weigh samples of coffee &
compute ranges of samples; Plot

19. Hotel Example
You’re manager of a 500-
room hotel. You want to
analyze the time it takes to
deliver luggage to the room.
For 7 days, you collect data
on 5 deliveries per day. Is
the process in control?

20. Hotel Data
Day Delivery Time
1 7.30 4.20 6.10 3.45 5.55
2 4.60 8.70 7.60 4.43 7.62
3 5.98 2.92 6.20 4.20 5.10
4 7.20 5.10 5.19 6.80 4.21
5 4.00 4.50 5.50 1.89 4.46
6 10.10 8.10 6.50 5.06 6.94
7 6.77 5.08 5.90 6.90 9.30

21. R &X Chart Hotel Data
Sample
Day Delivery Time Mean Range
1 7.30 4.20 6.10 3.45 5.55 5.32
7.30 + 4.20 + 6.10 + 3.45 + 5.55
5
Sample Mean =

22. R &X Chart Hotel Data
Sample
Day Delivery Time Mean Range
1 7.30 4.20 6.10 3.45 5.55 5.32 3.85
Largest Smallest
Sample Range = 7.30 - 3.45

23. R &X Chart Hotel Data
Sample
Day Delivery Time Mean Range
1 7.30 4.20 6.10 3.45 5.55 5.32 3.85
2 4.60 8.70 7.60 4.43 7.62 6.59 4.27
3 5.98 2.92 6.20 4.20 5.10 4.88 3.28
4 7.20 5.10 5.19 6.80 4.21 5.70 2.99
5 4.00 4.50 5.50 1.89 4.46 4.07 3.61
6 10.10 8.10 6.50 5.06 6.94 7.34 5.04
7 6.77 5.08 5.90 6.90 9.30 6.79 4.22

24. R Chart Control Limits
UCL D R
LCL D R
R
R

k
R
R
i
i
k
 
 
 
4
3
1
From Exhibit 6.13
Sample Range
at Time i
# Samples

25. Control Chart Limits
n A2 D3 D4
2 1.88 0 3.278
3 1.02 0 2.57
4 0.73 0 2.28
5 0.58 0 2.11
6 0.48 0 2.00
7 0.42 0.08 1.92

26. R Chart Control Limits
R
R
1  3 85 4 27 4 22
 
k
i
i
k
 
  
7
3 894
. . .
.


27. R Chart Solution
From 6.13
(n = 5)
R
R
 
1
 
k
i
i
k
. . .
UCL D R
R
4
LCL D R
R
  

   
   
3
3 85 4 27 4 22
7
3 894
(2.11) (3.894) 8 232
(0)(3.894) 0
.
.


28. R Chart Solution
R, Minutes
8
6
4
2
0
1 2 3 4 5 6 7
Day
UCL

29. X Chart Control Limits
k
R
R
UCL  X  A 
R
X
k
X
k
i
i
k
i
i
X
2
 
  1 
 1
Sample
Mean at
Time i
Sample
Range
at Time i
# Samples

30. X Chart Control Limits
UCL X A R
2
LCL X A R
X
2
 X

1 1
k
R
R
k
X
X
i
i
k
i
i
k
  
  
   
From
Table 6-13

31. X Chart Control Limits
UCL X A R
2
LCL X A R
X
2
 X

1 1
k
R
R
k
X
X
i
i
k
i
i
k
  
  
   
From 6.13
Sample
Mean at
Time i
Sample
Range
at Time i
# Samples

32. Exhibit 6.13 Limits
n A2 D3 D4
2 1.88 0 3.278
3 1.02 0 2.57
4 0.73 0 2.28
5 0.58 0 2.11
6 0.48 0 2.00
7 0.42 0.08 1.92

33. R &X Chart Hotel Data
Sample
Day Delivery Time Mean Range
1 7.30 4.20 6.10 3.45 5.55 5.32 3.85
2 4.60 8.70 7.60 4.43 7.62 6.59 4.27
3 5.98 2.92 6.20 4.20 5.10 4.88 3.28
4 7.20 5.10 5.19 6.80 4.21 5.70 2.99
5 4.00 4.50 5.50 1.89 4.46 4.07 3.61
6 10.10 8.10 6.50 5.06 6.94 7.34 5.04
7 6.77 5.08 5.90 6.90 9.30 6.79 4.22

34. X Chart Control Limits
X
X

 
k
R
R

k
i
i
k
i
i
k
  

 
  



1
1
5 32 6 59 6 79
7
5 813
3 85 4 27 4 22
7
3 894
. . .
.
. . .
.



35. X Chart Control Limits
From 6.13
(n = 5)
X
X

 
k
R
R

k
i
i
k
i
i
k

5 . 32 6 . 59 6 .
79

. . .
UCL X A R
X
  

 
  

.
.
     


1
1
2
7
5 813
3 85 4 27 4 22
7
3 894
5 . 813 0 . 58 * 3 . 894 8 .
060

36. X Chart Solution
From 6.13
(n = 5)
X
X

 
k
R
R

k
i
i
k
i
i
k

5 . 32 6 . 59 6 .
79

. . .
UCL X A R
X
LCL X A R
X
  

 
  

. .
    
    


1
1
2
2
7
5 813
3 85 4 27 4 22
7
.
3 894
5 813 (0 58)
.
5 . 813 (0 .
58)(3.894) = 3.566
(3.894) = 8.060

37. X Chart Solution*
X, Minutes
8
6
4
2
0
1 2 3 4 5 6 7
Day
UCL
LCL

38. Thinking Challenge
You’re manager of a 500-
room hotel. The hotel owner
tells you that it takes too
long to deliver luggage to the
room (even if the process
may be in control). What do
you do?
© 1995 Corel Corp.
N

39. Solution
 Redesign the luggage delivery process
 Use TQM tools
 Cause & effect diagrams
 Process flow charts
 Pareto charts
Method People
Material Equipment
Too
Long