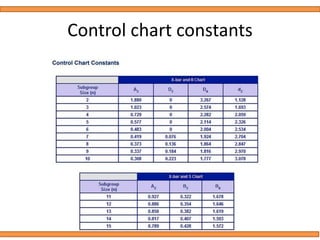
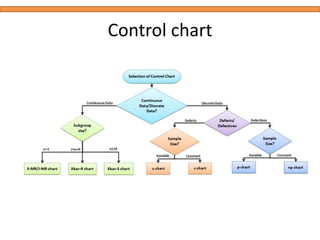
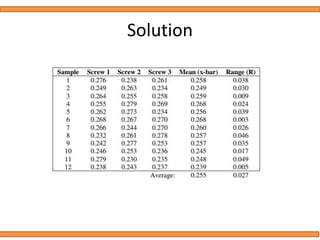
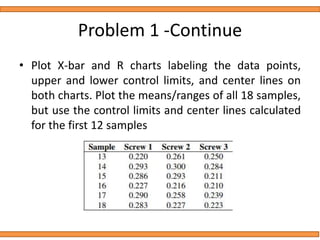
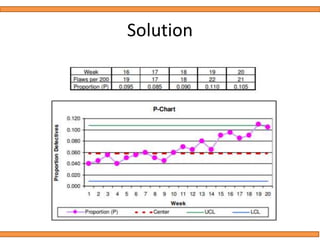
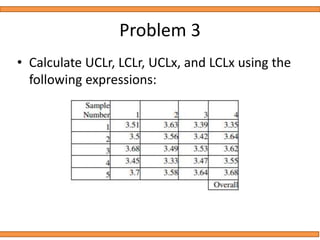
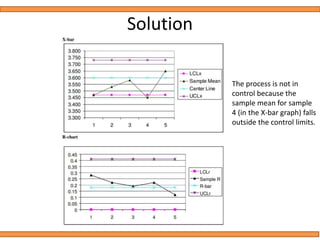
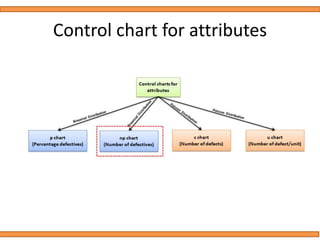
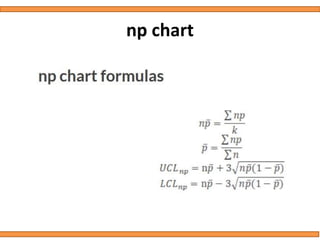
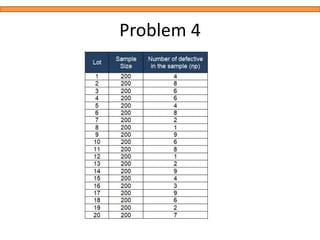
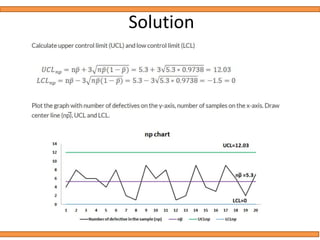
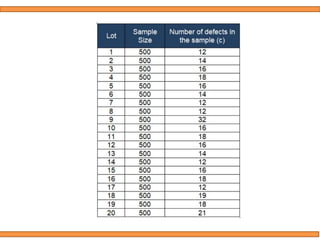
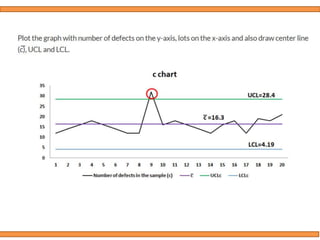
This document discusses statistical quality control using x-bar and r charts to monitor process variations over time, emphasizing the importance of subgroup sizes and control limits. It includes step-by-step procedures for calculating control limits and interpreting charts, along with examples of problems related to quality control in manufacturing processes. It also introduces np, c, and p charts for tracking defects and provides guidance on the creation and analysis of these charts.

1. STATISTICAL QUALITY CONTROL
PROBLEMS

2. • X-bar chart: The mean or average change in
process over time from subgroup values. The
control limits on the X-Bar brings the sample’s
mean and center into consideration.
• R-chart: The range of the process over the
time from subgroups values. This monitors the
spread of the process over the time.

3. Use X Bar R Control Charts When:
• Even very stable process may have some minor variations,
which will cause the process instability. X bar R chart will
help to identify the process variation over the time
• When the data is assumed to be normally distributed.
• X bar R chart is for subgroup size more than one (for I-MR
chart the subgroup size is one only) and generally it is used
when rationally collect measurements in subgroup size is
between two and 10 observations.
• The X Bar S Control chart are to be consider when the
subgroup size is more than 10.
• When the collected data is in continuous (ie Length,
Weight) etc. and captures in time order

4. Control chart constants

5. Control chart

6. Procedure
• Calculate the average R value, or R-bar, and
plot this value as the centerline on the R
chart.
• Based on the subgroup size, select the
appropriate constant, called D4, and multiply
by R-bar to determine the Upper Control Limit
for the Range Chart. All constants are available
from the reference table.
UCL (R) = R-bar x D4

7. Procedure
• If the subgroup size is between 7 and 10,
select the appropriate constant, called D3, and
multiply by R-bar to determine the Lower
Control Limit for the Range Chart.
• There is no Lower Control Limit for the Range
Chart if the subgroup size is 6 or less.
• LCL(R) = R-bar x D3

8. Procedure
• Using the X-bar values for each subgroup,
compute the average of all Xbars, or X-bar-bar
(also called the Grand Average). Plot the X-bar-
bar value as the centerline on the X Chart
• Calculate the X-bar Chart Upper Control Limit, or
upper natural process limit, by multiplying R-bar
by the appropriate A2 factor (based on subgroup
size) and adding that value to the average (X-bar-
bar).
• UCL (X-bar) = X-bar-bar + (A2 x R-bar)

9. Procedure
• Calculate the X-bar Chart Lower Control Limit,
or lower natural process limit, for the X-bar
chart by multiplying R-bar by the appropriate
A2 factor (based on subgroup size) and
subtracting that value from the average (X-
barbar).
• LCL(X-bar) = X-bar-bar - (A2 x R-bar)
• Plot the Lower Control Limit on the X-bar
chart.

10. Problem 1
• Calculate the 3ϭ control limits for X-bar and R
charts based on the first 12 samples reflecting
the process before any problems were
denounced.

11. Solution

12. Solution

13. Problem 1 -Continue
• Plot X-bar and R charts labeling the data points,
upper and lower control limits, and center lines on
both charts. Plot the means/ranges of all 18 samples,
but use the control limits and center lines calculated
for the first 12 samples

15. Problem 1 -Continue
• Do you feel that the screw production process
is in control? Is there something suspicious?
The graphs confirm that the customers
complaints are justified – it really seems as if the
variation in the screw diameters has increased
significantly. The R-chart suggests significant
differences even within single samples! Clearly
some corrective measures have to be taken to
bring this process back under control!

16. Problem 2
• Calculate the 3ϭ control limits for the
supplier’s manufacturing process based on the
first 15 weeks (i.e. weeks 1-15, when the
quality of the alloy did not seem to be an
issue).

17. Problem 2

18. Problem 2 -Continue
• Create the SPC chart including the weekly
data, control limits, and the center line. Plot
the defective fractions of all 20 weeks, but use
the control limits and the center line of the
first 15 weeks!! Interpret the chart – what
does it suggest?

19. Solution

20. Inference from chart
• Clearly there is an upward tendency in the fraction of
defective packages of alloy. Even though the problem was
not noticed before week 15, it seems as if this process
started already in week 9.
• The magnitude of the fluctuations is not as alarming as is
the steady upward tendency. Even though only the very last
weeks reveal defective fractions outside the control limits,
the graph gives the impression that the fractions will keep
on increasing in future.
• Whatever the reasons for this increase might be, it leads to
severe quality problems of Screwed’s final products and
cannot be accepted. Definitely this problem should be
looked into more carefully …

21. Problem 3
• Calculate UCLr, LCLr, UCLx, and LCLx using the
following expressions:

22. Solution

23. Solution
The process is not in
control because the
sample mean for sample
4 (in the X-bar graph) falls
outside the control limits.

24. • np chart is one of the quality control charts is
used to assess trends and patterns in counts
of binary events (e.g., pass, fail) over time.
• np chart requires that the sample size of the
each subgroup be the same and compute
control limits based on the binomial
distribution.

25. Control charts for attribute data
• u chart is for the number of defects per unit
• c chart is for the number of defects.
• p chart plots the proportion of defective
items.
• The np chart reflects integer numbers rather
than proportions.
• The applications of np chart are basically the
same as the applications for the p chart.

26. Control chart for attributes

27. Assumptions of Attribute charts: np
chart
• The probability of non-conformance is the
same for each item
• There should be two events (pass or fail), and
they are mutually exclusive
• Each unit is independent of the other
• The testing procedure should be the same for
each lot

29. np chart

30. Problem 4
• Smartbulbs Inc is a famous LED bulb
manufacturer. Supervisor drawn randomly
constant sample size of 200 bulbs every hour
and reported the number of defective bulbs
for each lot. Based on the given data, prepare
the control chart for the number of defectives
and determine process is in statistical control?

31. Problem 4

32. Solution
• no of lots k = 20
• Σnp = 105
• Σn = 4000
• Compute p̅ = total number of defectives / total
number of samples =Σnp/Σn =105/4000= 0.0263
• 1- p̅ = 0.9738
• Calculate centreline np̅ = total number of
defectives/no of lots = Σnp/k =105/20 = 5.3

33. Solution

34. C Chart
• c chart is also known as the control chart for defects
(counting of the number of defects). It is generally used
to monitor the number of defects in constant size
units.
• There may be a single type of defect or several
different types, but the c chart tracks the total number
of defects in each unit and it assumes the underlying
data approximate the Poisson distribution.
• The unit may be a single item or a specified section of
items—for example, scratches on plated metal,
number of insufficient soldering in a printed circuit
board.

35. C Chart

36. C Chart

37. How do you Create a C Chart
• Determine the subgroup size. The subgroup size must be
large enough for the c chart; otherwise, control limits may
not be accurate when estimated from the data.
• Count the number of defects in each sample
• Compute centreline c̅ = total number of defects / number
of samples =Σc/k
• Calculate upper control limit (UCL) and low control limit
(LCL). If LCL is negative, then consider it as 0.
• Plot the graph with number of defects on the y-axis, lots on
the x-axis: Draw centerline, UCL and LCL. Use these limits to
monitor the number of defects going forward.
• Finally, interpret the data to determine whether the
process is in control.

38. Problem
• Mobile charger supplier drawn randomly
constant sample size of 500 chargers every
day for quality control test. Defects in each
charger are recorded during testing. Based on
the given data, draw the appropriate control
chart and comment on the state of control.