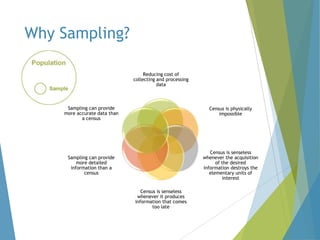
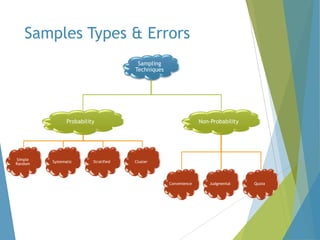
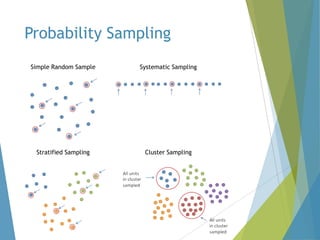
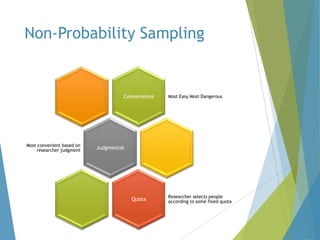
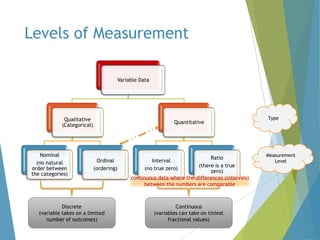
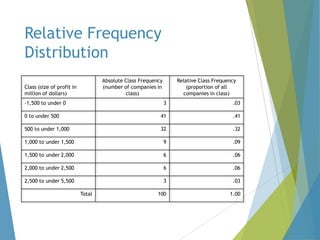
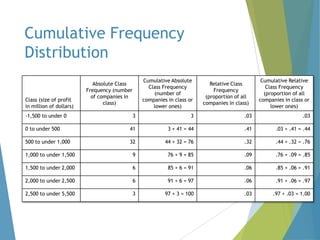
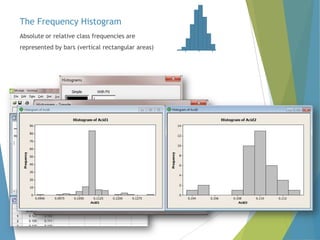
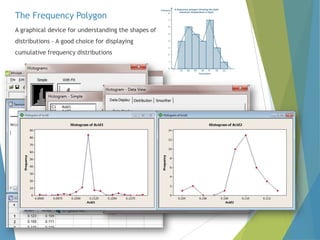
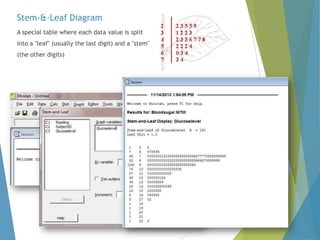
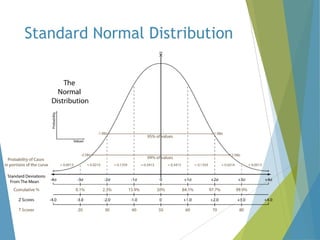
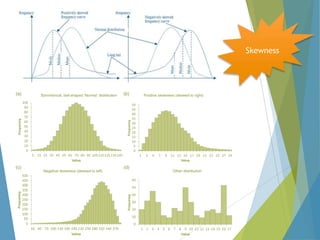
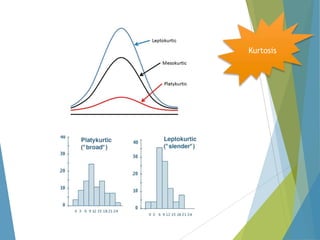
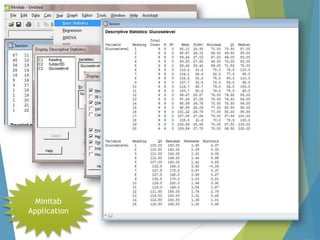
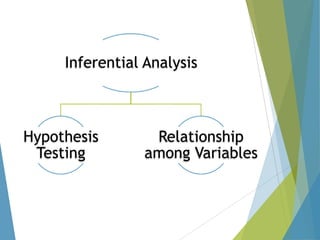
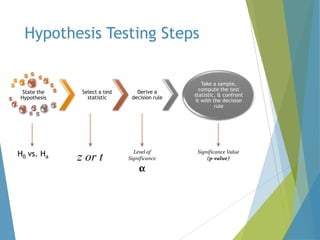
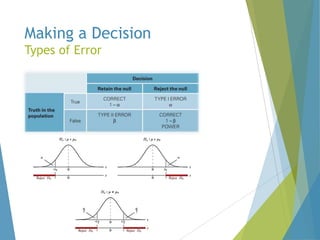
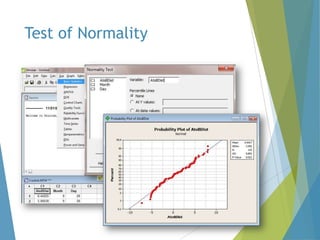
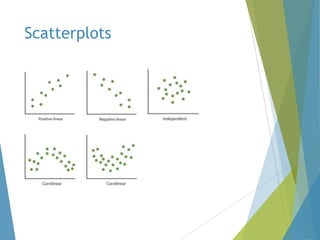
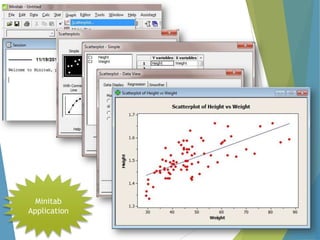
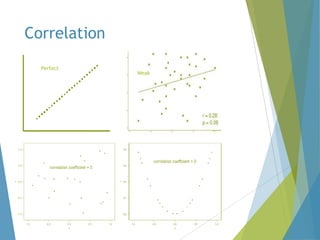
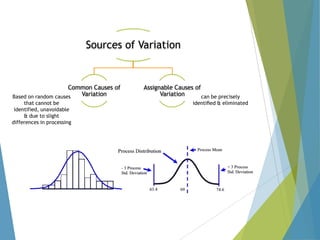
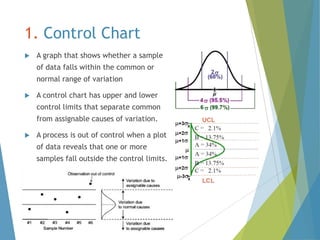
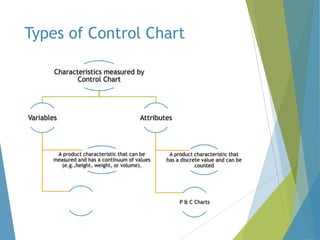
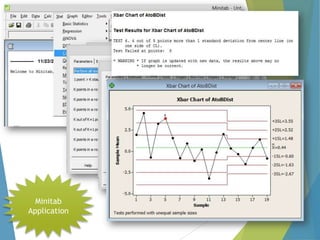
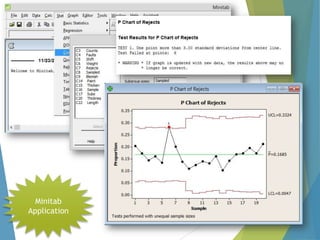
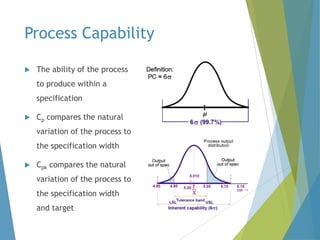
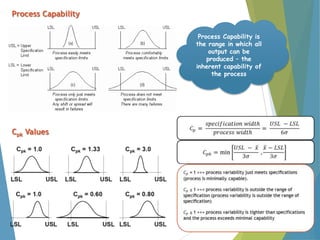
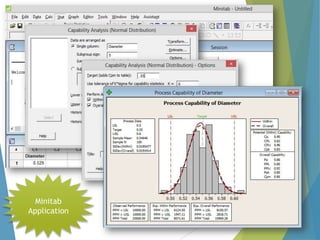
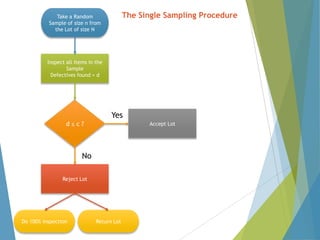
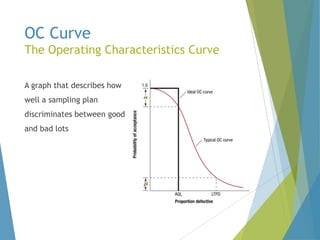
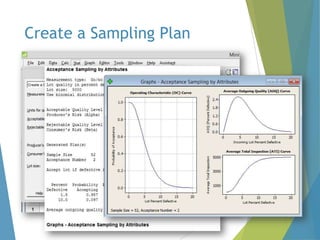
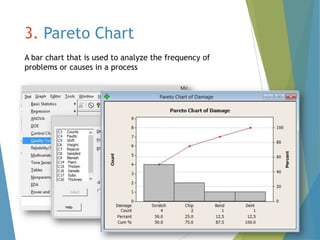
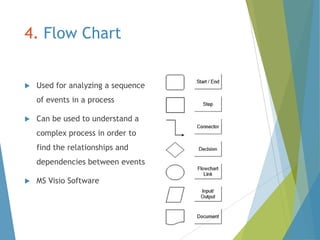
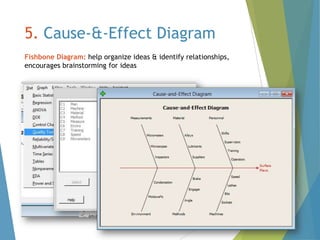
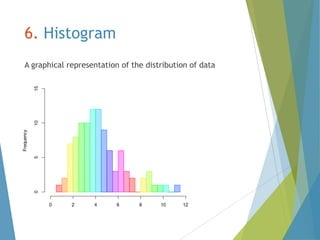
This document provides an overview of statistical process control and related quality control techniques. It discusses descriptive statistics, statistical process control methods including the seven basic quality tools, and acceptance sampling. Statistical process control is identified as the most important statistical quality control tool because it can identify changes or variations in quality during the production process using methods like control charts. Control charts, check sheets, Pareto charts, flow charts and other tools are explained as part of statistical process control. Acceptance sampling procedures and how they manage producer and consumer risks are also summarized.

1. Statistical Process Control
Relating Applied Statistics to Quality Control

2. Contents

Introduction to Statistics



Descriptive Analysis
Inferential Analysis
Statistical Quality Control

Descriptive Statistics

Statistical Process Control (SPC)


SPC: 7 Basic Quality Tools
Acceptance Sampling

3. Introduction to Statistics
The Nature of Statistics and the Collection of Data

5. What is Statistics?
A branch of mathematics used
to summarize, analyze, and
interpret a group of numbers or
observations

6. Descriptive Statistics
Procedures used to summarize, organize, and make sense of a set of scores
or observations
Typically presented graphically, in tabular form (in tables), or as summary
statistics (single values)

7. Inferential Statistics
Procedures used that allow researchers to infer or generalize observations
made with samples to the larger population from which they were selected

8. Before we go…
Which type of tables, graphs,
and summary measures to use
with our data?
Data
Measurements or observations
that are typically numeric
Datum = raw score
(a single measurement or observation)

9. Data Concepts
Sources of Data
Internal vs.
External
Data
Elementary
Units &
Variables
Population
vs. Sample
Qualitative
vs.
Quantitative
Variables
Observational
Study (Survey)
Experiment
Census
Sample
Survey

10. Why Sampling?
Reducing cost of
collecting and processing
data
Sampling can provide
more accurate data than
a census
Census is physically
impossible
Sampling can provide
more detailed
information than a
census
Census is senseless
whenever the acquisition
of the desired
information destroys the
elementary units of
interest
Census is senseless
whenever it produces
information that comes
too late

11. Samples Types & Errors
Sampling
Techniques
Probability
Simple
Random
Systematic
Stratified
Non-Probability
Cluster
Convenience
Judgmental
Quota

12. Probability Sampling
Simple Random Sample
Systematic Sampling
Stratified Sampling
Cluster Sampling

13. Non-Probability Sampling
Convenience
Most convenient based on
researcher judgment
Most Easy Most Dangerous
Judgmental
Quota
Researcher selects people
according to some fixed quota

14. Sampling Error

Random Error: arise from
random fluctuations in
the measurements

Systematic Error (Bias):
consistent and repeatable
(constant offset)

15. Variable Data Types
Qualitative = Quality
(Categorical Variables)
Quantitative = Quantity
(Numeric Variables)

16. Levels of Measurement
Variable Data
Qualitative
(Categorical)
Nominal
(no natural
order between
the categories)
Quantitative
Ordinal
(ordering)
Discrete
(variable takes on a limited
number of outcomes)
Ratio
(there is a true
zero)
continuous data where the differences (intervals)
between the numbers are comparable
Interval
(no true zero)
Continuous
(variables can take on tiniest
fractional values)
Type
Measurement
Level

17. Minitab 16 Software
A statistical software used to
analyze data
o
Calculating basic statistics
o
Graphing data
o
Running hypothesis tests

18. Starting Minitab 16

19. Minitab Interface

20. Opening a Worksheet

21. Descriptive Statistics
The Effective Presentation of Data

22. The Presentation of Data
Tables & Graphs
Tables
Absolute Frequency
Distribution
Graphs
Frequency
Histograms
Relative Frequency
Distribution
Bar & Column Charts
Cumulative Frequency
Distribution
Line Graphs
Pie Charts
Stem-&-Leaf
Diagrams
Box-&-Whisker
Diagrams

23. Absolute Frequency
Distribution
Absolute Class Frequency (number of companies in class)
Class (size of profit in
million of dollars)
Tally
Count
-1,500 to under 0
||
|
0 to under 500
|| |||| |||| |||| |||
|||| |||| |||| ||||
41
500 to under 1,000
|| |||| |||| |||
|||| |||| |||| |
32
1,000 to under 1,500
|| ||
||||
9
1,500 to under 2,000
||
|||
6
2,000 to under 2,500
||
|||
6
2,500 to under 5,500
||
|
3
Total
3
100

24. Relative Frequency
Distribution
Absolute Class Frequency
(number of companies in
class)
Class (size of profit in
million of dollars)
-1,500 to under 0
Relative Class Frequency
(proportion of all
companies in class)
3
.03
0 to under 500
41
.41
500 to under 1,000
32
.32
1,000 to under 1,500
9
.09
1,500 to under 2,000
6
.06
2,000 to under 2,500
6
.06
2,500 to under 5,500
3
.03
100
1.00
Total

25. Cumulative Frequency
Distribution
Class (size of profit
in million of dollars)
-1,500 to under 0
Cumulative Absolute
Class Frequency
(number of
companies in class or
lower ones)
Absolute Class
Frequency (number
of companies in
class)
Relative Class
Frequency
(proportion of all
companies in class)
Cumulative Relative
Class Frequency
(proportion of all
companies in class or
lower ones)
3
3
.03
.03
0 to under 500
41
3 + 41 = 44
.41
.03 + .41 = .44
500 to under 1,000
32
44 + 32 = 76
.32
.44 + .32 = .76
1,000 to under 1,500
9
76 + 9 = 85
.09
.76 + .09 = .85
1,500 to under 2,000
6
85 + 6 = 91
.06
.85 + .06 = .91
2,000 to under 2,500
6
91 + 6 = 97
.06
.91 + .06 = .97
2,500 to under 5,500
3
97 + 3 = 100
.03
.97 + .03 = 1.00

26. Producing Frequency Table

27. The Frequency Histogram
Absolute or relative class frequencies are
represented by bars (vertical rectangular areas)

28. The Frequency Polygon
A graphical device for understanding the shapes of
distributions - A good choice for displaying
cumulative frequency distributions

29. Bar & Column Charts
A chart with rectangular bars with lengths
proportional to the values that they represent.
The bars can be plotted vertically or
horizontally.

30. Histograms vs. Bar Graphs

31. Line Graph
A graph that shows information
that is connected in some way
(such as change over time)

32. Pie Chart
A special chart that uses "pie slices"
to show relative sizes of data

33. Stem-&-Leaf Diagram
A special table where each data value is split
into a "leaf" (usually the last digit) and a "stem"
(the other digits)

35. Box-&-Whisker Diagram (Boxplot)
A way of summarizing a set of data measured on
an interval scale - used to show the shape of the
distribution, its central value, and variability

36. The Presentation of Data
Summary Measures
Continuous
Measures of
Central
Tendency
(Location)
Mean µ
Median M
Mode Mo
Quartiles (Percentiles)
Ordinal
Nominal
Continuous
Ordinal
Continuous
Range
Variance σ2
Standard Deviation σ
Measures of
Dispersion
(Variability)
Measures of
Shape
Proportion
π
Skewness Sk
Kurtosis K
Continuous

37. Standard Normal Distribution

38. Statistics Formulas
Descriptive Statistics
Statistic
Formula
Mean
Median (50% Quartile)
Mode
Most frequent value
Range
Maximum - Minimum
Variance
Standard Deviation
Skewness
Kurtosis
Quartiles
Cut into
4 equal
parts
Order
Data
Cuts = Quartiles

39. Skewness

40. Kurtosis

41. Minitab
Application

42. Inferential Statistics

43. Inferential Analysis
Hypothesis
Testing
Relationship
among Variables

44. Hypothesis Testing
(Significance Testing)
A systematic approach to assessing
tentative beliefs about reality.
It involves confronting those beliefs
with evidence and deciding, in
light of this evidence, whether the
beliefs can be maintained as
reasonable or must be discarded as
untenable.

45. Hypothesis Testing Steps
State the
Hypothesis
H0 vs. Ha
Select a test
statistic
z or t
Derive a
decision rule
Level of
Significance
α
Take a sample,
compute the test
statistic, & confront
it with the decision
rule
Significance Value
(p-value)

46. Making a Decision
Types of Error

47. Test of Normality

48. Relationship among
Variables
Relationship between two
variables can be checked by
drawing scatterplots or running
statistical tests.

49. Scatterplots

50. Minitab
Application

51. Correlation
Perfect
Weak

52. Minitab
Application

53. Testing Relationship among
Variables
Variables
Test
Both Variables are Nominal
Chi-square
Independent Variable is Nominal &
T-Test (Independent Variable has only two
Dependent Variable is Interval or Ratio
categories)
ANOVA (Independent Variable has more
than two categories)
Both Variables are Interval or Ratio
Correlation or Regression

54. Chi-Square X2 Test
Testing the Alleged Independence of two
Qualitative Variables
Contingency Table
A table that classifies data
according to two or more
categories, associated with each
of two qualitative variables that
may or may not be statistically
independent
It shows all possible
combinations of categories, or
contingencies, which counts for
its name.

55. T-Test
How to test for differences between
means from two separate groups of
subjects.

56. ANOVA
Analysis of Variance
Used to determine whether there
are any significant differences
between the means of three or
more independent (unrelated)
groups

58. Regression
Simple Regression Analysis
A statistical technique that
establishes an equation that allows
the unknown value of one variable
to be estimated from the known
value of one other variable

59. Statistical Quality Control
The general category of statistical tools used to evaluate
organizational quality

60. Statistical Quality
Control (SQC)
Descriptive Statistics
Statistical Process Control
(SPC)
Acceptance Sampling

61. Descriptive Statistics
Statistics used to describe quality
characteristics and relationships
Acceptance Sampling
Statistical Process
Control (SPC)
A statistical tool that involves
inspecting a random sample of the
The process of randomly inspecting
a sample of goods and deciding
whether to accept the entire lot
based on the results
output from a process and
deciding whether the process is
Process Capability
producing products with
The ability of a production process to
characteristics that fall within a
meet or exceed preset specifications
predetermined range
All three of these statistical quality control categories are helpful in measuring and evaluating
the quality of products or services. However, statistical process control (SPC) tools are used most
frequently because they identify quality problems during the production process.

62. Why SPC is the Most
Important Tool of the SQC?

Measure the value of a quality characteristic

Help to identify a change or variation in
some quality characteristic of the product
or process

63. Some Information about SPC

SPC can be applied to any process.

There is inherent variation in any process which can be
measured and “controlled”.

SPC doesn’t eliminate variation, but it does allow the user to
track special cause variation.

“SPC is a statistical method of separating variation resulting
from special causes from natural variation and to establish and
maintain consistency in the process, enabling process
improvement.” (Goetsch & Davis, 2003. p. 631)

64. Sources of Variation
Common Causes of
Variation
Based on random causes
that cannot be
identified, unavoidable
& due to slight
differences in processing
Assignable Causes of
Variation
can be precisely
identified & eliminated

65. Descriptive Statistics

Describing certain
characteristics of a product &
a process

Measures of Central Tendency
(mean)

Measures of Variability
(standard deviation & range)

Measures of the Distribution
of Data

66. Statistical Process Control
Methods – 7 Basic Quality Tools
Control Chart
Check Sheet
Pareto Chart
Flow Chart
Cause-&-Effect
Diagram
Histogram
Scatter Diagram

67. 1. Control Chart

A graph that shows whether a sample
of data falls within the common or
normal range of variation

A control chart has upper and lower
control limits that separate common
from assignable causes of variation.

A process is out of control when a plot
of data reveals that one or more
samples fall outside the control limits.

68. Types of Control Chart
Characteristics measured by
Control Chart
Variables
Attributes
A product characteristic that can be
measured and has a continuum of values
(e.g.,height, weight, or volume).
A product characteristic that
has a discrete value and can be
counted
P & C Charts

69. Control Charts for Variables
Range (R) Charts



70. Minitab
Application

71. Control Charts for Attributes
P-Charts
C-Charts



72. Minitab
Application

73. Process Capability

The ability of the process
to produce within a
specification

Cp compares the natural
variation of the process to
the specification width

Cpk compares the natural
variation of the process to
the specification width
and target

74. Process Capability
Process Capability is
the range in which all
output can be
produced – the
inherent capability of
the process
Cpk Values

75. Minitab
Application

76. Acceptance Sampling
An inspection procedure used to
determine whether to accept or reject a
specific quantity of materials
Acceptance Sampling
Sampling Plans
Producer’s Risk &
Consumer’s Risk
Managing Levels of
Risk

77. Sampling Plan

A plan for acceptance sampling that precisely specifies the
parameters of the sampling process and the
acceptance/rejection criteria

No 100% Inspection

The most widely used sampling plans are given by Military
Standard (MIL-STD-105E)

Determines the quality level of an incoming shipment or at
the end of production

Judges whether quality level is within the level that has
been predetermined

78. Types of Sampling Plans
Single-Sampling Plan
Sequential-Sampling Plan
A decision to accept or reject a
lot based on the results of one
random sample from the lot.
A plan in which the consumer randomly
selects items from the lot and inspects
them one by one.
Double-Sampling Plan
A plan in which management
specifies two sample sizes and two
acceptance numbers; if the quality
of the lot is very good or very bad,
the consumer can make a decision
to accept or reject the lot on the
basis of the first sample, which is
smaller than in the single-sampling
plan.
Sampling by Attribute
Sampling by Variable

79. The Single Sampling Procedure
Take a Random
Sample of size n from
the Lot of size N
Inspect all items in the
Sample
Defectives found = d
Yes
d≤c?
Accept Lot
No
Reject Lot
Do 100% Inspection
Return Lot

80. Acceptance Sampling Risks
The Lot is actually Good
The Lot is actually Bad
The Lot is Accepted
Correct Decision
Confidence = 1 – α
Incorrect Decision
β Risk (Consumer’s Risk)
The Lot is Rejected
Incorrect Decision
α Risk (Producer’s Risk)
Correct Decision
Power = 1 - β

81. OC Curve
The Operating Characteristics Curve
A graph that describes how
well a sampling plan
discriminates between good
and bad lots

82. Quality & Risk Decisions

Acceptable Quality Level (AQL): The small percentage of
defects that consumers are willing to accept.

Producer’s Risk (α): The chance that a lot containing an
acceptable quality level will be rejected.

Lot Tolerance Proportion Defective (LTPD): The upper
limit of the percentage of defective items consumers are
willing to tolerate.

Consumer’s Risk (β): The chance of accepting a lot that
contains a greater number of defects than the LTPD limit.

83. Average Outgoing Quality
(AOQ)


84. Create a Sampling Plan

85. Compare a Sampling Plan

86. 2. Check Sheet
A simple document that is used for collecting data in realtime and at the location where the data is generated.

87. 3. Pareto Chart
A bar chart that is used to analyze the frequency of
problems or causes in a process

88. 4. Flow Chart

Used for analyzing a sequence
of events in a process

Can be used to understand a
complex process in order to
find the relationships and
dependencies between events

MS Visio Software

89. 5. Cause-&-Effect Diagram
Fishbone Diagram: help organize ideas & identify relationships,
encourages brainstorming for ideas

90. 6. Histogram
A graphical representation of the distribution of data

91. 7. Scatterplot
A graph of plotted points that show the relationship
between two sets of data

92. “
Thank You!
Presenter:
Marwa Abo Amra
statistician.marwa@gmail.com
”