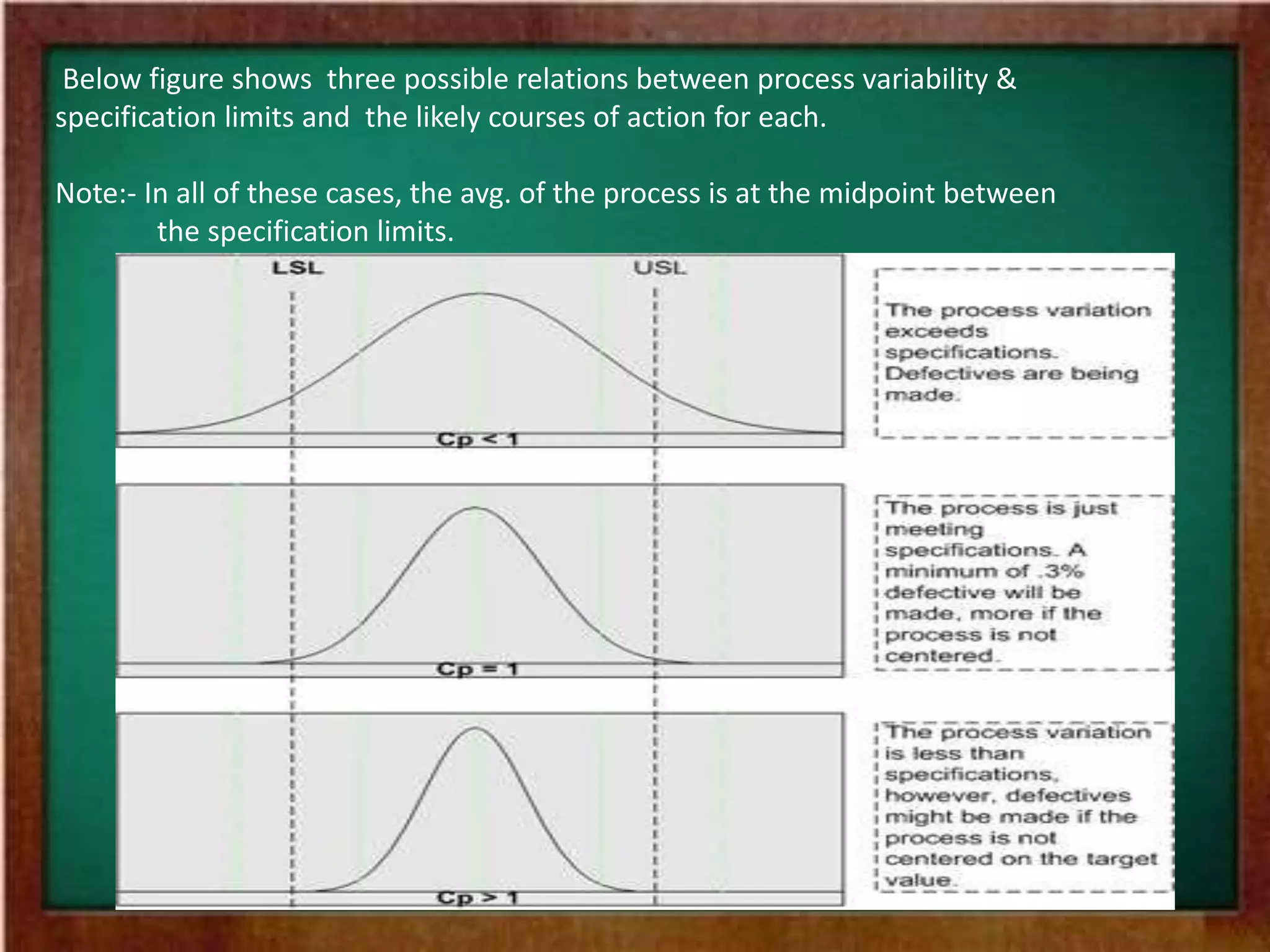
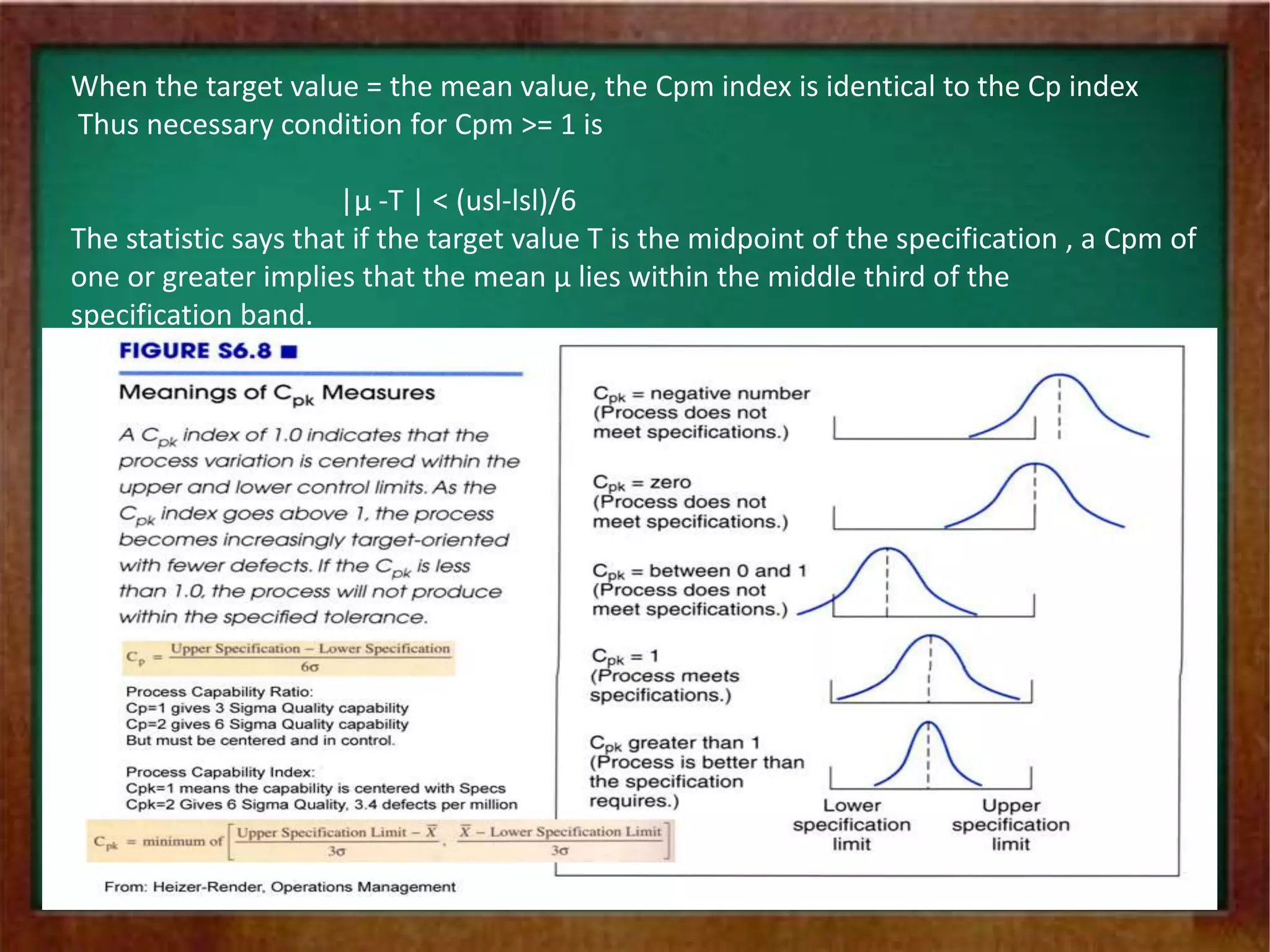
The document discusses process capability and defines key terms related to process capability. It provides the standard formula for process capability using 6 sigma and explains how process capability is compared to specification limits. It then discusses different process capability indices including Cp, Cpk, and Cpm. It explains how these indices measure both potential and actual process capability. The document also discusses limitations of the Cp index and the use of Cpk to address process centering. It describes how to calculate confidence intervals for process capability ratios and discusses some key process performance metrics.

1. PROCESS CAPABILITY
Presented By,
Prnv B. Gujjar
M.Q.P.M. (3ed sem.)
Dept. of Statistics .

2. Definition:-
“ Process Capability is the measured, inherent variation of
the product turned out by a process”.
In the Definition of Process Capability
1.) PROCESS REFERS to some unique combination of machines, tools, methods,
materials & people engaged in production. It is often feasible & illuminating
to separate & quantify the effect of the variables entering this combination.
2.) CAPABILITY REFERS to an ability, based on tested performance, to achieve
measurable results.
3.) MEASURABLE CAPABILITY REFERS to the fact that process capability is
quantified from data that , in turn, are the results of measurement of work
performed by the process.
4.) INHERENT CAPABILITY REFERS to the product uniformity resulting from
a process that is in a state of statistical control “instantaneous reproducibility”
is a synonym for inherent capability.
5.) PRODUCT is measured because product variation is the end result.

3. Standardize formula for Process Capability
# Process Capability = +3σ or -3σ ( a total of 6σ)
Where,
σ shows the standard deviation of Process under a state of statistical control.
# If the process is centered at the nominal specification & follows a normal
probability distribution ,99.73% of production will fall within +3σ or -3σ of the
normal specification.
# Some industrial process operate under a state of statistical control.
For such processes,
The computed process capability of 6σ can be compared directly to specification
limits, A judgments of adequacy can be made.
# A process is said to be capable when the output always conforms to
the process specifications.

4. Specification limit & Natural Tolerance limit
• Specification Limits reflect what the customer needs.
• Determined by the Customer
• A Specific Quantitative Definition of “Fitness for Use”
• Not Necessarily Related to a Particular Production Process
• Not Represented on Control Charts
• Natural Tolerance Limits (a.k.a. Control Limits) reflect what the
process is capable of actually delivering.
• Determined by the inherent central tendency and dispersion of the production process
• Represented on Control Charts to help determine whether the process is “under
control”
• A process under control may not deliver products that meet specifications
• A process may deliver acceptable products but still be out of control

5. Process Capability Index
It is a dimensionless number that is used to represent the ability to meet customer
specification limits. This index compares the variability of characteristics to
the specification limits. Three basic process capability indices commonly used are
Cp ,Cpk & Cpm.
The Cp index represent process capability in relation to the specified tolerance of a
Characteristic divided by the natural process variation for a process in state of statistical
Control,
Where,
USL is upper specification limit
LSL is lower specification limit
6σ is the natural process variation
In simple terms,

6. The process Capability index uses both the process variability & the process specifications
to determine whether the process is “ capable “.
A capable process is one where all he measurements fall inside the specification limit.
Table shows selected capability ratios & the corresponding level of defects,
assuming that the process avg. is midway between the specification limit.

7. Below figure shows three possible relations between process variability &
specification limits and the likely courses of action for each.
Note:- In all of these cases, the avg. of the process is at the midpoint between
the specification limits.

8. Example for understanding the value of Cp

9. Limitation of Cp Index & To Generate Cpk
The Cp index is limited in its use since it doesn’t address the centering of the process
Relative to he specification limit. For that reason ,the Cpk was developed and
I is defind as
Cpk = min[ Cpku,Cpkl]
Where, Cpku= =Upper Process Capability Index
Cpkl= =Lower Process Capability Index
If Cp = Cpk the process is center at the midpoint of the specifications.
Cpk <Cp the process is off center. The magnitude of Cpk relative to Cp is a direct
measure of how off-centre the process is operating.

10. We usually say that ,
1.) Cp measures potential Capability in the process,
It means, an estimate is obtained of what the process can do under certain
condition : i.e. variability under short-run defined conditions for a process in state
of statistical control.
2.) Cpk measures actual Capability or process performance,
It means, an estimate of capability provide a picture of what the process is
doing over extended period of time. A statistical control is also assumed.
3.) When Cpk < 0 the implication is that the process mean lies outside the specifications.
If Cpk < -1 , the entire process lies outside the specification limits.
# The large value of Cpk doesn’t really tell us anything about the location of the mean
in the interval from Lsl to Usl
One way to address this difficulty is to use a process capability ratio that is a
better indicator of centering.
one such ratio is
Where, τ is the square root of expected squared deviation from target.

11. When the target value = the mean value, the Cpm index is identical to the Cp index
Thus necessary condition for Cpm >= 1 is
|µ -T | < (usl-lsl)/6
The statistic says that if the target value T is the midpoint of the specification , a Cpm of
one or greater implies that the mean µ lies within the middle third of the
specification band.

12. Short –term & Long-term Capability
1.) Cp & Cpk represent long-term Capability while Pp & Ppk represent short –
term capability
Using Ppk for less than a 30 day production run ( hat is , short-term)
& Cpk for
everything thereafter ( that is long term).
2.) Long-term variability = Short-term Variability + 1.5 σ shift.
The interpretation is based on the underlying assumption of six-sigma,
which is that a process will drift or shift +1.5σ or -1.5σ in the long-erm.
When this drift is taken into account,6σ process performance equates to 3.4 ppm
Otherwise 4.5σ process performance equates to 3.4 ppm

13. Process Performance metrics
Mainly 5 process performance metrics given below
1.) Defect per unit (DPU)
2.) Defect per million opportunities (DPMO)
3.) Throughput yield
throughput yield = e-DPU
4.) Parts per million
ppm = DPU * 1000000
5.) Rolled throughput yield (RTY)
It applies to the yield from a series of process & is found by multiplying the individual
process yields. If a product goes trough four process whose yields are 0.994, 0.987, 0.951
& 0.990 than
RTY = (0.994) * (0.987) * ( 0.951) * (0.990)
= 6.924

14. Confidence Interval on process capability ratios
1.) Much of the industrial use of process capability ratios focuses in computing &
interpreting the point estimate of the desired quantity.
2.) Practitioners often forget that estimate values of Cp & Cpk are simply point estimates
and as such, are subject to statistical fluctuation.
3.) An alternative that should become standard practice is o report confidence interval
for PCR.
4.) It is easy to find a confidence interval for the “ first generation “ ratio Cp .If we replace σ
by S in the equation for Cp. We produce the usual point estimator Cp.
If the quality characteristic follows a normal distribution, then a 100(1-alpha)%
confidence interval on Cp is obtained from equations.

15. Cpm
• You are almost never going to use
this, but for completeness…..
• In some processes you will not
target the center point.
• Example cutting impellers you
want to cut an impeller diameter
between 196 and 200 mm
• It may be cheaper to bias the
target cut towards say 199mm
instead of 198mm
• So in this case if we target
199mm we want to measure
the process against the target
instead of the center point
Cpm = Cp/[1+((Xbar-T)^2/s^2)]; Where T is the
target value. Explained above.