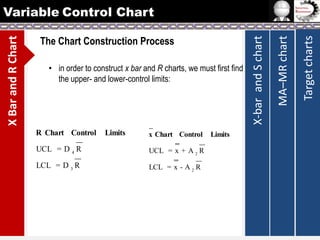
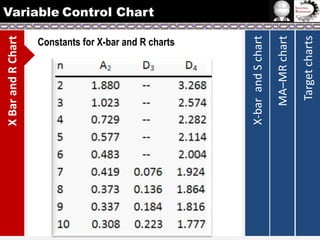
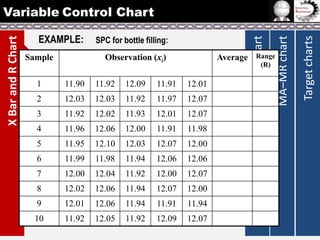
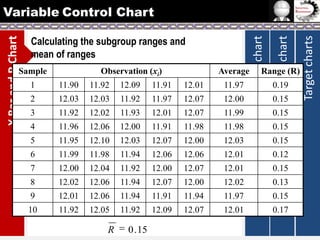
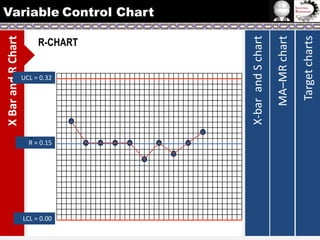
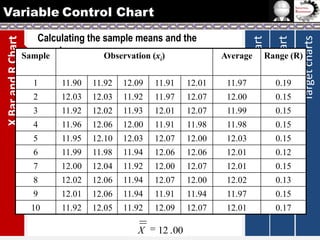
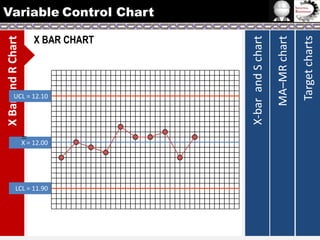
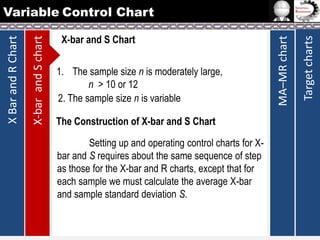
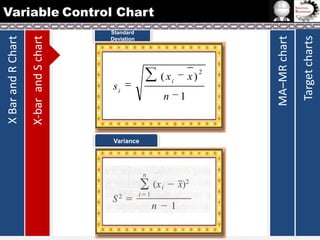
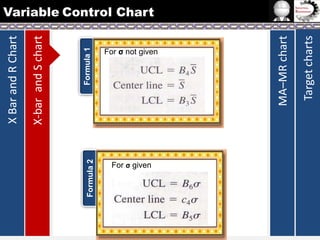
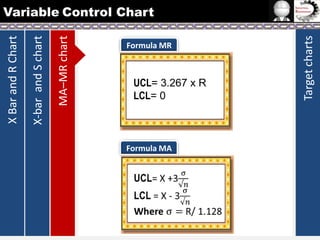
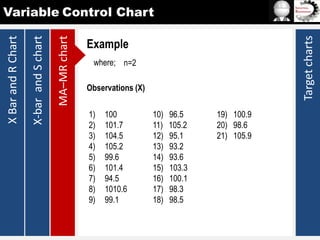
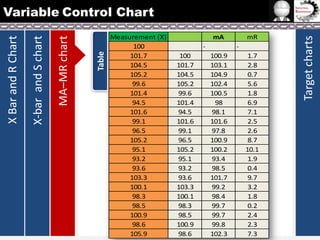
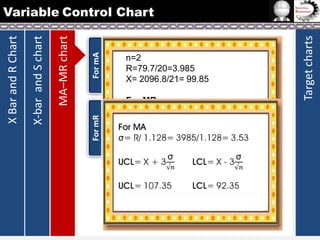
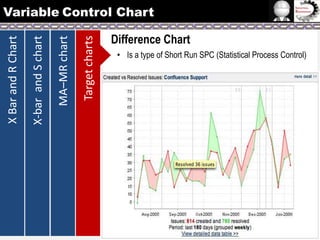
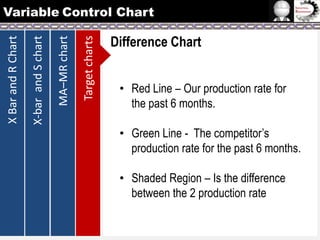
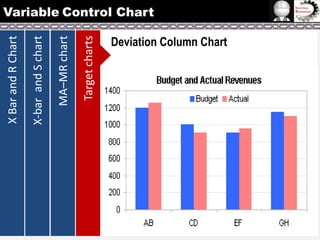
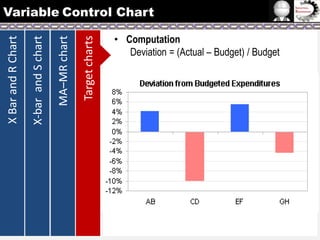
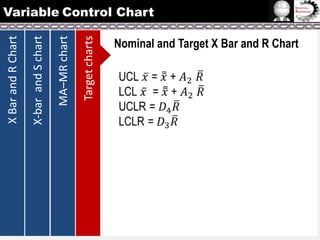
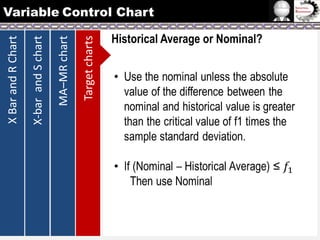
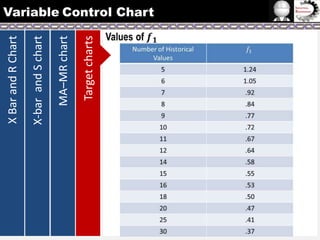
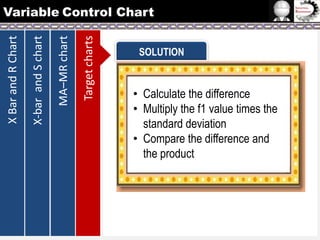
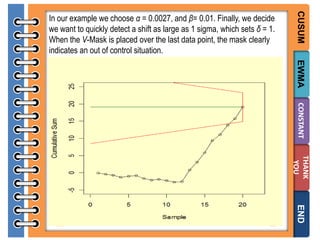
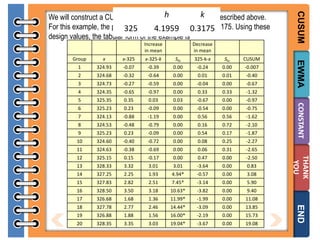
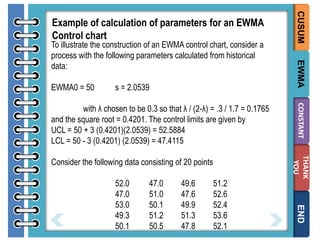
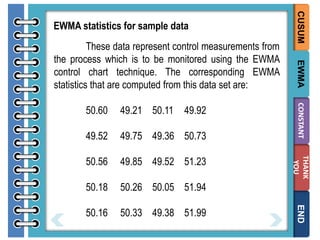
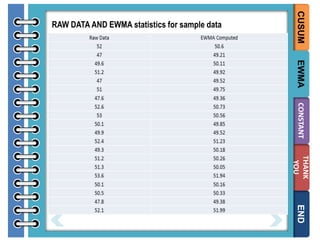
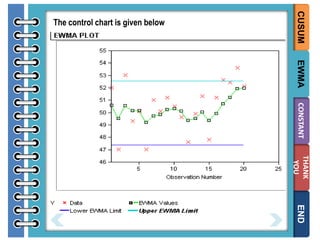
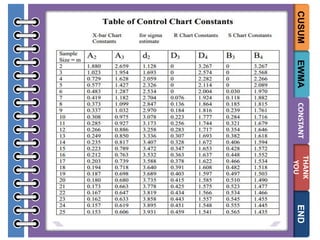
The document provides information on different types of control charts used for statistical process control, including X-bar and R charts, X-bar and S charts, and moving average-moving range (MA-MR) charts. X-bar and R charts monitor both the average value and variation in a process over time using subgroup means and ranges. The construction process, chart interpretation, and an example are described. X-bar and S charts are similar but use standard deviation instead of range. MA-MR charts are beneficial when data is collected slowly over time using moving averages and ranges to monitor process location and variation.

1. • used to detect/identify assignable causes.
always has a central line for the average, an
upper line.
• for the upper control limit and a lower line for the
lower control limit.
• also known as Shewhart charts or processbehavior charts
Target charts
MA–MR chart
• used to determine if a manufacturing or
business process is in a state of statistical
control
X-bar and S chart
Introduction
X-bar and R chart
Control Chart

2. • charts applied to data that follow a continuous distribution.
• Are typically used used in pairs:
• monitors process average
• monitors the variation in the process
• A quality characteristic that is measured on a
numerical scale is called a variable.
• dimension
• length, width
• weight
• temperature
• volume
Target charts
Variable Control Charts
MA–MR chart
• charts applied to data that follow a discrete distribution.
X-bar and S chart
Attributes Control Charts
X-bar and R chart
Control Chart

3. • Moving average–moving range chart
(also called MA–MR chart)
• Target charts (also called difference
charts, deviation charts and nominal
charts)
• CUSUM (cumulative sum chart)
• EWMA (exponentially weighted moving
average chart)
Target charts
• X-bar and s chart
MA–MR chart
• X-bar and R chart (also called
averages and range chart)
X-bar and S chart
Variable Control Charts
X-bar and R chart
Control Chart

4. • is advantageous in the following situations:
• The sample size is relatively small (n ≤
10)
• The sample size is constant
• Humans must perform the calculations for
the chart
Target charts
MA–MR chart
• is a type of control chart used to
monitor variables data when samples are
collected atis a type of control chart used to
monitor variables data when samples are
collected at regular intervals from
a business or industrial process.
X-bar and S chart
X Bar and R Chart
Variable Control Chart

5. R Chart
• is a control chart that is used to monitor
process variation when the variable of interest
is a quantitative measure.
• Range Chart
Target charts
• is used to monitor the average value, or mean,
of a process over time.
• Mean chart or average chart
MA–MR chart
X bar Charts
X-bar and S chart
X Bar and R Chart
Variable Control Chart

6. • If the R chart indicates the sample
variability is in statistical control, the X bar
chart is examined to determine if the
sample mean is also in statistical control.
• If the sample variability is not in statistical
control, then the entire process is judged to
be not in statistical control regardless of
what the X bar chart indicates.
Target charts
• The R chart is examined first before
the X bar chart
MA–MR chart
Guidelines in X Bar and R Chart:
X-bar and S chart
X Bar and R Chart
Variable Control Chart

7. Target charts
Control chart is out of statistical control if:
MA–MR chart
Reading Control Charts
X-bar and S chart
X Bar and R Chart
Variable Control Chart

8. R Chart Control
Limits
x Chart Control
UCL = D 4 R
UCL = x + A 2 R
LCL = D 3 R
LCL = x - A 2 R
Limits
Target charts
• in order to construct x bar and R charts, we must first find
the upper- and lower-control limits:
MA–MR chart
The Chart Construction Process
X-bar and S chart
X Bar and R Chart
Variable Control Chart

9. X Bar and R Chart
Constants for X-bar and R charts
Target charts
MA–MR chart
X-bar and S chart
Variable Control Chart

10. 2. Find the range of each subgroup R(i) where
R(i)=biggest value - smallest value for each subgroup i.
3. Find the centerline for the R chart, denoted by
RBAR=summation of R(i)/ k
4. Find the UCL and LCL
5. Plot the subgroup data and determine if the process is
in statistical control.
Target charts
1. Select k successive subgroups where k is at least 20,
in which there are n measurements in each subgroup.
Typically n is between 1 and 9. 3, 4, or 5
measurements per subgroup is quite common.
MA–MR chart
Steps in Constructing an R chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

11. Observation (xi)
Average
1
11.90
11.92
12.09
11.91
12.01
2
12.03
12.03
11.92
11.97
12.07
3
11.92
12.02
11.93
12.01
12.07
4
11.96
12.06
12.00
11.91
11.98
5
11.95
12.10
12.03
12.07
12.00
6
11.99
11.98
11.94
12.06
12.06
7
12.00
12.04
11.92
12.00
12.07
8
12.02
12.06
11.94
12.07
12.00
9
12.01
12.06
11.94
11.91
11.94
10
11.92
12.05
11.92
12.09
12.07
Range
(R)
Target charts
Sample
SPC for bottle filling:
MA–MR chart
EXAMPLE:
X-bar and S chart
X Bar and R Chart
Variable Control Chart

12. Observation (xi)
Average
Range (R)
1
11.90
11.92
12.09
11.91
12.01
11.97
2
12.03
12.03
11.92
11.97
12.07
12.00
3
11.92
12.02
11.93
12.01
12.07
11.99
4
11.96
12.06
12.00
11.91
11.98
11.98
5
11.95
12.10
12.03
12.07
12.00
12.03
0.15
6
11.99
11.98
11.94
12.06
12.06
12.01
0.12
7
12.00
12.04
11.92
12.00
12.07
12.01
0.15
8
12.02
12.06
11.94
12.07
12.00
12.02
0.13
9
12.01
12.06
11.94
11.91
11.94
11.97
0.15
10
11.92
12.05
11.92
12.09
12.07
12.01
0.17
R
0 . 15
0.19
0.15
0.15
0.15
Target charts
Sample
MA–MR chart
Calculating the subgroup ranges and
mean of ranges
X-bar and S chart
X Bar and R Chart
Variable Control Chart

13. ( 2 . 11 )( 0 . 15 )
LCL = D 3 R
( 0 )( 0 . 15 )
0
0.32
Target charts
UCL = D 4 R
MA–MR chart
Calculating the UCL and LCL
X-bar and S chart
X Bar and R Chart
Variable Control Chart

14. X Bar and R Chart
R-CHART
UCL = 0.32
R = 0.15
LCL = 0.00
Target charts
MA–MR chart
X-bar and S chart
Variable Control Chart

15. Target charts
1.Find the mean of each subgroup and the grand mean of all
subgroups.
2. Find the UCL and LCL
3. Plot the LCL, UCL, centerline, and subgroup means
4. Interpret the data using the following guidelines to
determine if the process is in control:
MA–MR chart
Steps in Constructing the X Bar Chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

16. Average
Range (R)
0.19
1
11.90
11.92
12.09
11.91
12.01
11.97
2
12.03
12.03
11.92
11.97
12.07
12.00
3
11.92
12.02
11.93
12.01
12.07
11.99
4
11.96
12.06
12.00
11.91
11.98
11.98
5
11.95
12.10
12.03
12.07
12.00
12.03
0.15
6
11.99
11.98
11.94
12.06
12.06
12.01
0.12
7
12.00
12.04
11.92
12.00
12.07
12.01
0.15
8
12.02
12.06
11.94
12.07
12.00
12.02
0.13
9
12.01
12.06
11.94
11.91
11.94
11.97
0.15
10
11.92
12.05
11.92
12.09
12.07
12.01
0.17
X
12 . 00
Target charts
i
MA–MR chart
Calculating the sample means and the
grand mean
Sample
Observation (x )
X-bar and S chart
X Bar and R Chart
Variable Control Chart
0.15
0.15
0.15

17. LCL = x - A 2 R
12
0 .58 ( 0 .15 )= 12 . 09
12 - 0 .58 ( 0 .15 )= 11 . 91
Target charts
UCL = x + A 2 R
MA–MR chart
Calculating the UCL and LCL
X-bar and S chart
X Bar and R Chart
Variable Control Chart

18. X = 12.00
LCL = 11.90
Target charts
UCL = 12.10
MA–MR chart
X BAR CHART
X-bar and S chart
X Bar and R Chart
Variable Control Chart

19. 1. The sample size n is moderately large,
n > 10 or 12
2. The sample size n is variable
The Construction of X-bar and S Chart
Setting up and operating control charts for Xbar and S requires about the same sequence of step
as those for the X-bar and R charts, except that for
each sample we must calculate the average X-bar
and sample standard deviation S.
Target charts
X-bar and S Chart
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

20. si
Variance
( xi
n
x)
1
2
Target charts
Standard
Deviation
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

21. Formula 2
Formula 1
X-bar and S chart
X Bar and R Chart
For σ not given
For σ given
Target charts
MA–MR chart
Variable Control Chart

22. Piston for automotive engine are produced
by a forging process. We wish to establish statistical
control of inside diameter of the ring manufactured
by this process using X-bar and S charts.
Twenty-five (25) samples, each of size five
(5), have been taken when we think the process is in
control. The inside diameter measurement data from
these samples are shown in table.
TABLE
Target charts
Example
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

23. UCL = x + B 4 S
74 . 001
LCL = x - B 3 S
1 . 435 ( 0 .0094 )= 74 . 014
74 . 001 - 0 . 565 ( 0 .0094 )= 73 . 996
Calculating the UCL and LCL (S Chart)
UCL = B
LCL = B
ANSWER-1
4
3
S
S
1 . 435 ( 0 .0094 )= 0 . 0135
0 . 565 ( 0 .0094 )= 0 . 0053
ANSWER-2
Table of Constant
Target charts
Calculating the UCL and LCL (X bar Chart)
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

24. MA-MR charts
• In situations where data are collected slowly over a period
of time, or where data are expensive to collect, moving
average charts are beneficial.
• Moving Average / Range Charts are a set of control charts
for variables data (data that is both quantitative and
continuous in measurement, such as a measured
dimension or time). The Moving Average chart monitors
the process location over time, based on the average of
the current subgroup and one or more prior subgroups.
The Moving Range chart monitors the variation between
the subgroups over time.
Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

25. MA–MR chart
X-bar and S chart
X Bar and R Chart
Image for MA- MR chart
Target charts
Variable Control Chart

26. Moving range (MR)
• n= number of measuremens in moving
average
• MR= l current measurement – previous
measurement I
• R = total of MRs/ total numbers of MRs
• X = total of measurements/ total numbers
of measurements
Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

27. Formula MR
UCL= 3.267 x R
LCL= 0
Formula MA
Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

28. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Example
where; n=2
Observations (X)
1)
2)
3)
4)
5)
6)
7)
8)
9)
100
101.7
104.5
105.2
99.6
101.4
94.5
1010.6
99.1
10)
11)
12)
13)
14)
15)
16)
17)
18)
96.5
105.2
95.1
93.2
93.6
103.3
100.1
98.3
98.5
19) 100.9
20) 98.6
21) 105.9

29. Measurement (X)
100
101.7
104.5
105.2
99.6
101.4
94.5
101.6
99.1
96.5
105.2
95.1
93.2
93.6
103.3
100.1
98.3
98.5
100.9
98.6
105.9
mA
100
101.7
104.5
105.2
99.6
101.4
94.5
101.6
99.1
96.5
105.2
95.1
93.2
93.6
103.3
100.1
98.3
98.5
100.9
98.6
mR
-
100.9
103.1
104.9
102.4
100.5
98
98.1
101.6
97.8
100.9
100.2
93.4
98.5
101.7
99.2
98.4
99.7
99.7
99.8
102.3
1.7
2.8
0.7
5.6
1.8
6.9
7.1
2.5
2.6
8.7
10.1
1.9
0.4
9.7
3.2
1.8
0.2
2.4
2.3
7.3
Target charts
Table
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

30. UCL= 3.267 x R
LCL= 0
= 3.267 X 3.985
= 13.02
Target charts
For mA
n=2
R=79.7/20=3.985
X= 2096.8/21= 99.85
For MR
For mR
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

31. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Target Chart

32. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Difference Chart
• Is a type of Short Run SPC (Statistical Process Control)

33. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Difference Chart
• Red Line – Our production rate for
the past 6 months.
• Green Line - The competitor’s
production rate for the past 6 months.
• Shaded Region – Is the difference
between the 2 production rate

34. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Deviation Column Chart
A
1
2
B
C
D
E
F
Budget and Actual Revenues
Budget
Actual
Dev
Pos Dev Neg Dev
3 AB
1200
1250
4.2%
4.2%
0.0%
4 CD
1000
900
-10.0%
0.0%
-10.0%
5 EF
900
950
5.6%
5.6%
0.0%
6 GH
1150
1100
-4.3%
0.0%
-4.3%

35. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Deviation Column Chart

36. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
• Computation
Deviation = (Actual – Budget) / Budget

37. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Short Run SPC Approaches
• Nominal Short Run SPC
• Target Short Run SPC

38. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Short Run Nominal X Bar and R Chart
• The nominal x bar and R chart is used to
monitor the behavior of a process running
different part numbers and still retain the
ability to assess control.
• This is done by coding the actual measured
readings in a subgroup as a variation from a
common reference point, in this case the
nominal print specification.

39. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Nominal and Target X Bar and R Chart

40. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Historical Average or Nominal?

41. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart

42. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
Example
Suppose the historical average based on
10 measurements taken from the last time a given
part number was run is 20.4 and the sample
standard deviation was 1.07. Determine if the
nominal of 20.0 or the historical average of 20.4
should be used.

43. Target charts
MA–MR chart
X-bar and S chart
X Bar and R Chart
Variable Control Chart
SOLUTION
• Calculate the difference
• Multiply the f1 value times the
standard deviation
• Compare the difference and
the product

44. CUSUM
EWMA
CONSTANT
THANK
YOU
END

45. EWMA
CONSTANT
CUSUM charts show cumulative sums of
subgroup or individual measurements from a
target value. CUSUM charts can help you decide
whether a process is in a state of statistical
control by detecting small, sustained shifts in the
process mean.
CUSUM
Cumulative Sum Chart Tab
THANK
YOU
END

46. EWMA
CONSTANT
THANK
YOU
END
• A visual procedure proposed by Barnard in 1959,
known as the V-Mask, is sometimes used to
determine whether a process is out of control. A VMask is an overlay shape in the form of a V on its
side that is superimposed on the graph of the
cumulative sums.
CUSUM
• CUSUM works as follows: Let us collect m samples,
each of size n, and compute the mean of each
sample. Then the cumulative sum (CUSUM) control
chart is formed. In either case, as long as the process
remains in control centered at , the CUSUM plot
will show variation in a random pattern centered
about zero. If the process mean shifts upward, the
charted CUSUM points will eventually drift upwards,
and vice versa if the process mean decreases.

47. CUSUM
EWMA
The origin point of the V-Mask (see diagram below) is placed on top
of the latest cumulative sum point and past points are examined to
see if any fall above or below the sides of the V. As long as all the
previous points lie between the sides of the V, the process is in
control. Otherwise (even if one point lies outside) the process is
suspected of being out of control.
CONSTANT
THANK
YOU
END

48. THANK
YOU
END
• We can design a V-Mask using h and k or we can use an alpha
and beta design approach. For the latter approach we must specify.
CONSTANT
• Are each the average of samples of size 4 taken from a process that
has an estimated mean of 325. Based on process data, the process
standard deviation is 1.27 and therefore the sample means have a
standard deviation of 1.27/(41/2) = 0.635.
EWMA
• An example will be used to illustrate the construction and application
of a V-Mask. The 20 data points 324.925, 324.675, 324.725, 324.350,
325.350, 325.225, 324.125, 324.525, 325.225, 324.600, 324.625,
325.150, 328.325, 327.250, 327.825, 328.500, 326.675, 327.775,
326.875, 328.350
CUSUM
• In practice, designing and manually constructing a V-Mask is a
complicated procedure. A CUSUM spreadsheet style procedure will
be shown below is more practical, unless you have statistical
software that automates the V-Mask methodology. Before describing
the spreadsheet approach, we will look briefly at an example of a VMask in graph form.

49. CUSUM
In our example we choose α = 0.0027, and β= 0.01. Finally, we decide
we want to quickly detect a shift as large as 1 sigma, which sets δ = 1.
When the V-Mask is placed over the last data point, the mask clearly
indicates an out of control situation.
EWMA
CONSTANT
THANK
YOU
END

50. EWMA
CONSTANT
THANK
YOU
END
We next move the V-Mask and
back to the first point that
indicated the process was out
of control. This is point number
14, as shown below. Most
users of CUSUM procedures
prefer tabular charts over the
V-Mask. The V-Mask is actually
a carry-over of the precomputer era. The tabular
method can be quickly
implemented by standard
spreadsheet software. To
generate the tabular form we
use the h and k parameters
expressed in the original data
units.
CUSUM
We next move the V-Mask and back to the first
point that indicated the process was out of control. This is
point number 14, as shown below.

51. Increase
in mean
Decrease
in mean
Shi
325-k-x
Slo
CUSUM
1
324.93
-0.07
-0.39
0.00
-0.24
0.00
-0.007
2
324.68
-0.32
-0.64
0.00
0.01
0.01
-0.40
3
324.73
-0.27
-0.59
0.00
-0.04
0.00
-0.67
4
324.35
-0.65
-0.97
0.00
0.33
0.33
-1.32
5
325.35
0.35
0.03
0.03
-0.67
0.00
-0.97
6
325.23
0.23
-0.09
0.00
-0.54
0.00
-0.75
7
324.13
-0.88
-1.19
0.00
0.56
0.56
-1.62
8
324.53
-0.48
-0.79
0.00
0.16
0.72
-2.10
9
325.23
0.23
-0.09
0.00
0.54
0.17
-1.87
10
324.60
-0.40
-0.72
0.00
0.08
0.25
-2.27
11
324.63
-0.38
-0.69
0.00
0.06
0.31
-2.65
12
325.15
0.15
-0.17
0.00
0.47
0.00
-2.50
13
328.33
3.32
3.01
3.01
-3.64
0.00
0.83
14
327.25
2.25
1.93
4.94*
-0.57
0.00
3.08
15
327.83
2.82
2.51
7.45*
-3.14
0.00
5.90
16
328.50
3.50
3.18
10.63*
-3.82
0.00
9.40
17
326.68
1.68
1.36
11.99*
-1.99
0.00
11.08
18
327.78
2.77
2.46
14.44*
-3.09
0.00
13.85
19
326.88
1.88
1.56
16.00*
-2.19
0.00
15.73
20
328.35
3.35
3.03
19.04*
-3.67
0.00
19.08
END
x-325-k
THANK
YOU
x-325
CONSTANT
x
EWMA
Group
CUSUM
h
k
We will construct a CUSUM tabular chart for the example described above.
For this example, the parameter are 4.1959 and k = 0.3175. Using these
h = 4.1959 0.3175
325
design values, the tabular form of the example is

52. Definition
CONSTANT
THANK
YOU
END
• In statistical quality control, the EWMA
chart (or exponentially-weighted moving average chart) is
a type of control chart used to monitor either variables or
attributes-type data using the
monitored business or industrial process's entire history of
output. While other control charts treat rational subgroups
of samples individually, the EWMA chart tracks
the exponentially-weighted moving average of all prior
sample means.
EWMA
• The Exponentially Weighted Moving Average (EWMA) is a
statistics for monitoring the process that averages the
data in a way that gives less and less weight to data as
they are further removed in time.
CUSUM
EWMA Control Charts

53. Where:
THANK
YOU
END
The equation is due to Roberts (1959).
CONSTANT
• EWMA0 is the mean of historical data (target)
• Yt is the observation at time t
• n is the number of observations to be monitored
including EWMA0
• 0 < λ ≤ 1 is a constant that determines the depth of
memory of the EWMA.
EWMA
EWMAt = λ Yt + (1 - λ) EWMAt-1 for t = 1, 2, ..., n.
CUSUM
The statistic that is calculated is:

54. THANK
YOU
where the factor k is either set equal 3 or
chosen using the Lucas and Saccucci (1990) tables.
The data are assumed to be independent and these
tables also assume a normal population.
CONSTANT
UCL = EWMA0 + ksewma
LCL = EWMA0 - ksewma
EWMA
The center line for the control chart is the
target value or EWMA0. The control limits are:
CUSUM
Definition of control limits for EWMA
END

55. Example of calculation of parameters for an EWMA
Control chart
CUSUM
EWMA0 = 50
EWMA
To illustrate the construction of an EWMA control chart, consider a
process with the following parameters calculated from historical
data:
s = 2.0539
47.0
51.0
50.1
51.2
50.5
49.6
47.6
49.9
51.3
47.8
51.2
52.6
52.4
53.6
52.1
END
52.0
47.0
53.0
49.3
50.1
THANK
YOU
Consider the following data consisting of 20 points
CONSTANT
with λ chosen to be 0.3 so that λ / (2-λ) = .3 / 1.7 = 0.1765
and the square root = 0.4201. The control limits are given by
UCL = 50 + 3 (0.4201)(2.0539) = 52.5884
LCL = 50 - 3 (0.4201) (2.0539) = 47.4115

56. 49.92
49.75 49.36 50.73
50.56
49.85 49.52 51.23
50.18
50.26 50.05 51.94
50.16
50.33 49.38 51.99
END
49.52
THANK
YOU
49.21 50.11
CONSTANT
50.60
EWMA
These data represent control measurements from
the process which is to be monitored using the EWMA
control chart technique. The corresponding EWMA
statistics that are computed from this data set are:
CUSUM
EWMA statistics for sample data

57. CUSUM
RAW DATA AND EWMA statistics for sample data
EWMA
CONSTANT
THANK
YOU
END

58. CUSUM
The control chart is given below
EWMA
CONSTANT
THANK
YOU
END

59. EWMA
CONSTANT
The red dots are the raw data; the jagged
line is the EWMA statistics over time. The chart tells
us that the process is in control because all EWMA
lie between the control limits. However, there seems
to be a trend upwards for the last 5 periods.
CUSUM
Interpretation of EWMA Control chart
THANK
YOU
END

60. CUSUM
EWMA
CONSTANT
THANK
YOU
END

61. CONSTANT
THANK
YOU
Alina, Jassfer D.
Alvarez, Son Robert C.
Bautista, Billy Joe
Calosa Gilbert
Cristobal, Arnel Mark John
Mercado, Kim Nath
EWMA
Group 5 QCT
CUSUM
THANK YOU
END

62. CUSUM
EWMA
Group 5 QCT
CONSTANT
END
THANK
YOU
END