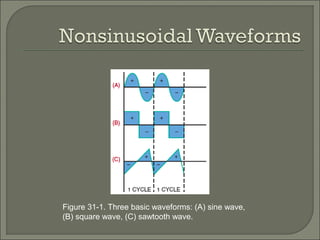
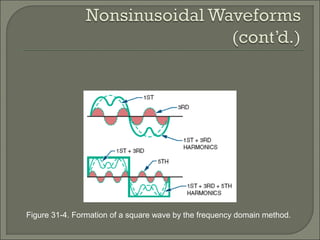
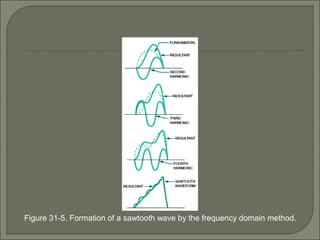
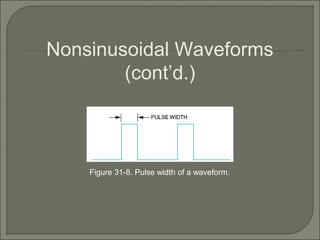
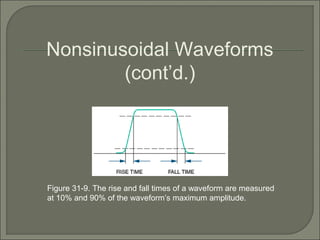
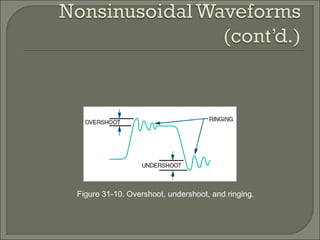
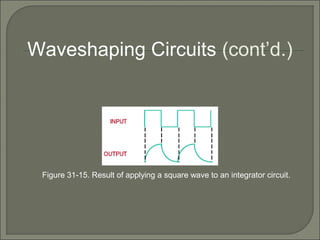
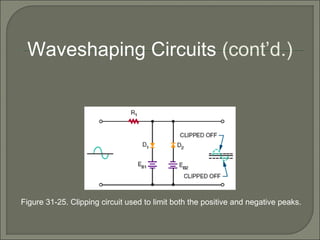
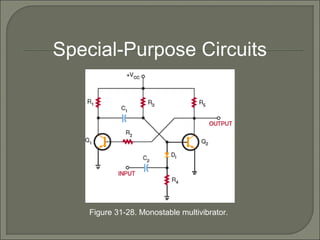
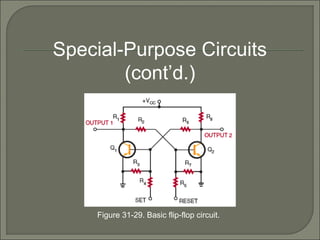
This document discusses waveshaping circuits. It introduces common waveforms like sine, square, and sawtooth waves. It describes how square and sawtooth waves can be formed using the frequency domain concept of combining sine waves. Key concepts for analyzing waveforms like pulse width, duty cycle, rise/fall times, overshoot, and ringing are also covered. The document examines how RC circuits can change waveforms by integrating or differentiating them. It also looks at monostable multivibrators that produce one output pulse per input, and bistable multivibrators known as flip-flops that have two stable states.

1. Waveshaping Circuits

2. Figure 31-1. Three basic waveforms: (A) sine wave,
(B) square wave, (C) sawtooth wave.

3. Figure 31-4. Formation of a square wave by the frequency domain method.

4. Figure 31-5. Formation of a sawtooth wave by the frequency domain method.

5. Figure 31-8. Pulse width of a waveform.
Nonsinusoidal Waveforms
(cont’d.)

6.  Duty cycle
• Ratio of the pulse width to the period
• Can be represented as a percentage:
Duty cycle = pulse width/period

7. Figure 31-9. The rise and fall times of a waveform are measured
at 10% and 90% of the waveform’s maximum amplitude.
Nonsinusoidal Waveforms
(cont’d.)

8. Figure 31-10. Overshoot, undershoot, and ringing.

9. Figure 31-11. Differentiator circuit.
Waveshaping Circuits

10. Figure 31-12. Result of applying a square wave to a differentiator circuit.
Waveshaping Circuits (cont’d.)

11. Figure 31-14. Integrator circuit.
Waveshaping Circuits (cont’d.)

12. Figure 31-15. Result of applying a square wave to an integrator circuit.
Waveshaping Circuits (cont’d.)

13. Figure 31-17. Basic series diode clipping circuit.
Waveshaping Circuits (cont’d.)

14. Figure 31-25. Clipping circuit used to limit both the positive and negative peaks.
Waveshaping Circuits (cont’d.)

15. Figure 31-27. Diode clamper circuit.
Waveshaping Circuits (cont’d.)

16. Figure 31-28. Monostable multivibrator.
Special-Purpose Circuits

17. Figure 31-29. Basic flip-flop circuit.
Special-Purpose Circuits
(cont’d.)

18.  Waveforms can be changed from one
shape to another using electronic circuits
 The frequency domain concept
• All periodic waveforms are made of sine waves
 Key concepts introduced in the chapter:
• Pulse width, duty cycle, rise and fall time,
undershoot, overshoot, and ringing

19.  An RC circuit can be used to change the
shape of a complex waveform
 A monostable multivibrator (one-shot
multivibrator) produces one output pulse
for each input pulse
 Bistable multivibrators have two stable
states and are called flip-flops