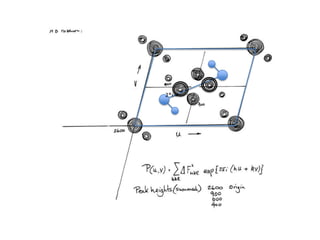
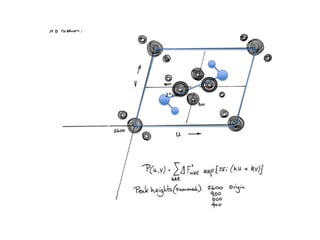
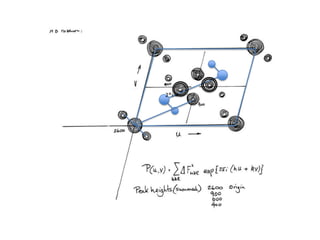
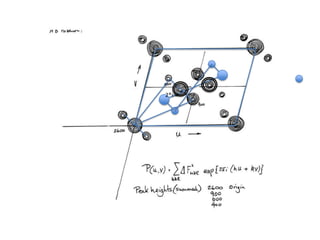
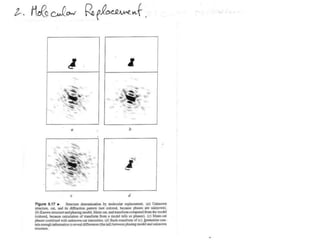
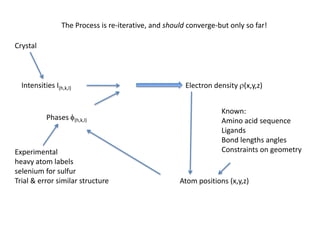
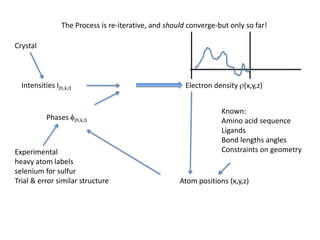
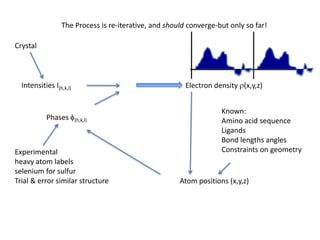
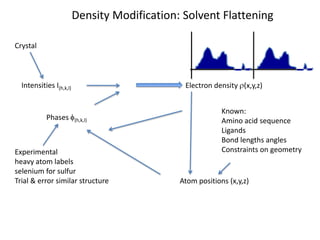
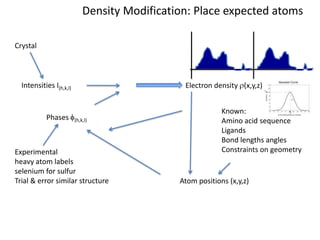
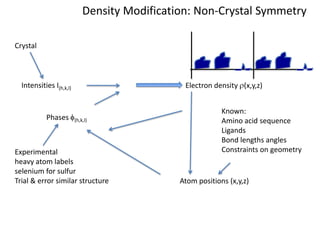
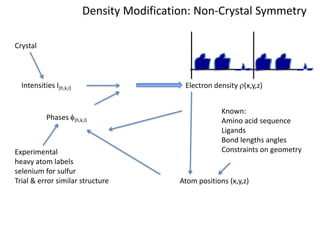
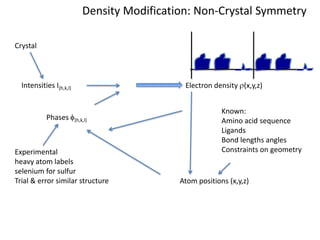
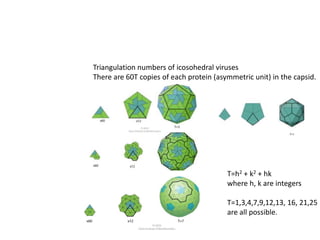
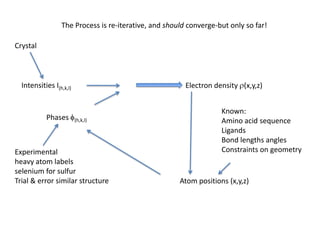
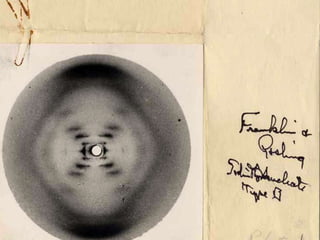
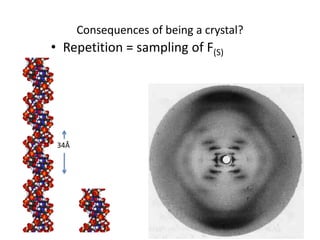
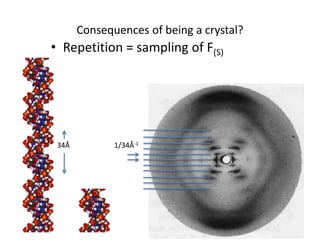
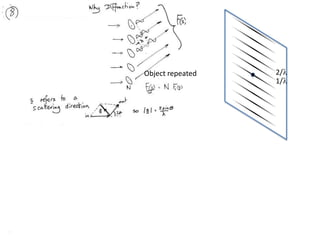
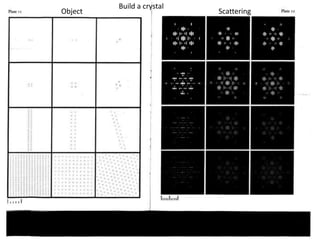
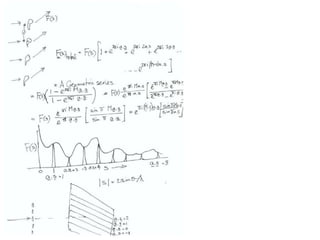
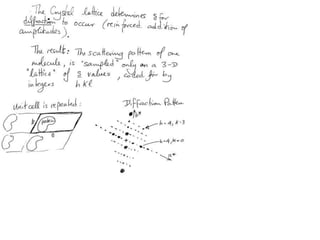
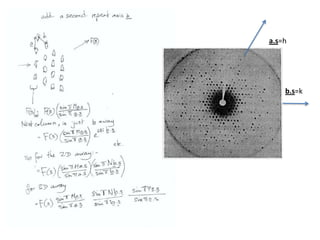
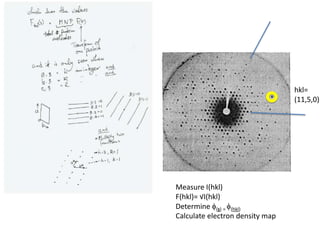
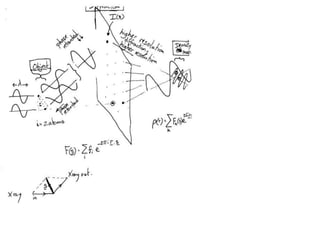
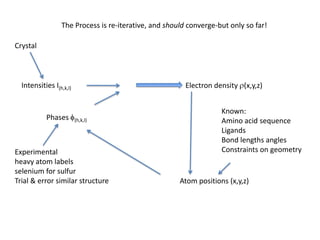
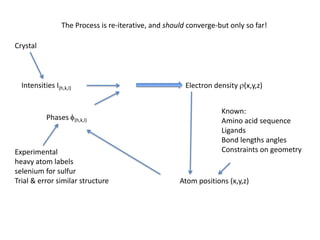
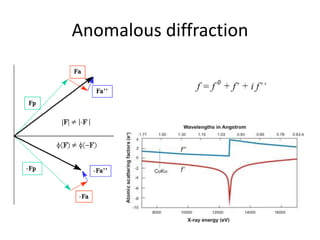
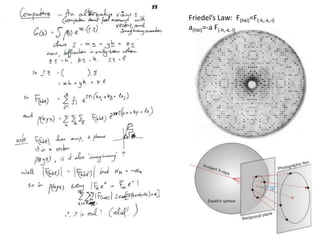
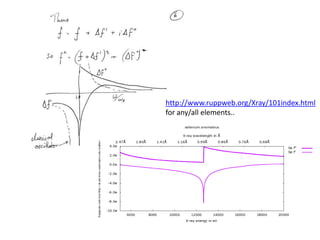
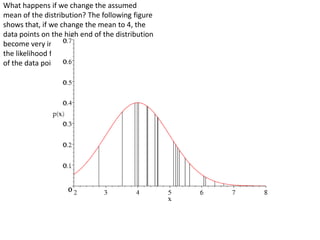
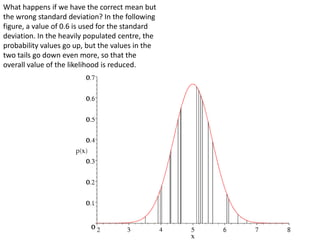
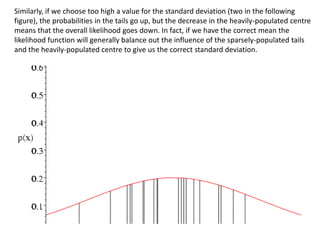
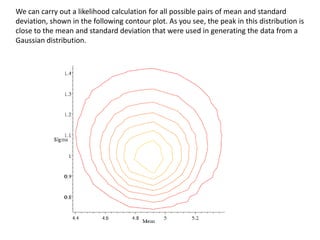
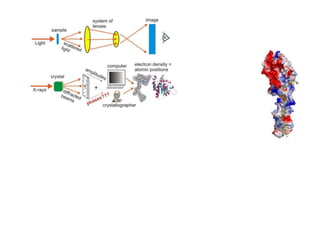
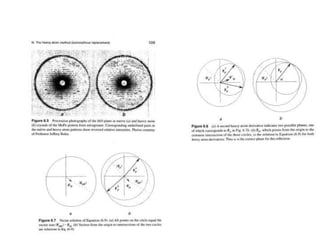
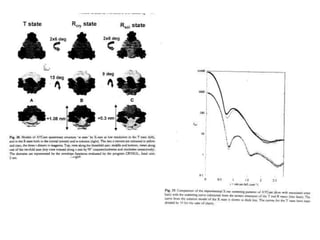
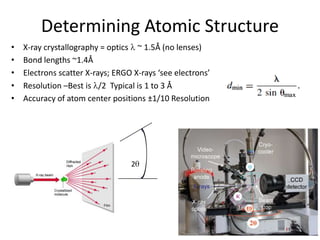
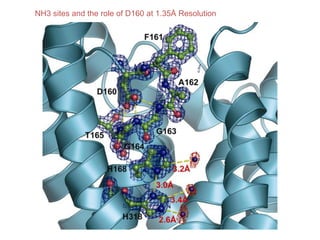
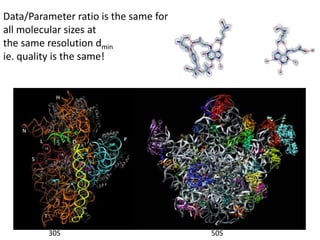
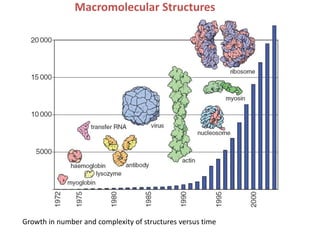
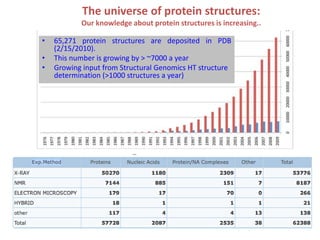
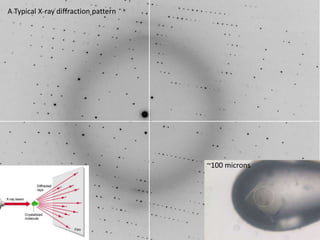
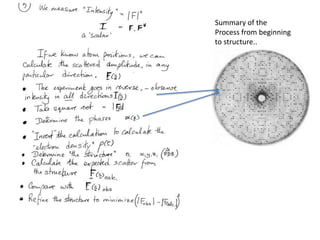
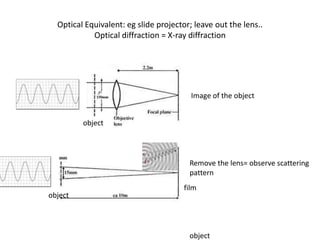
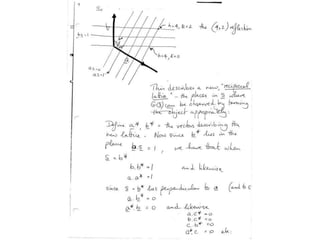
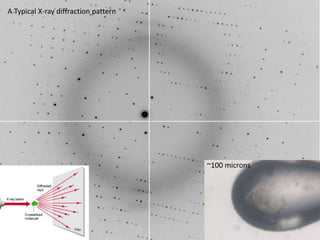
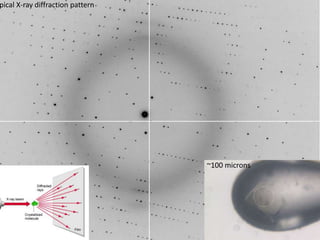
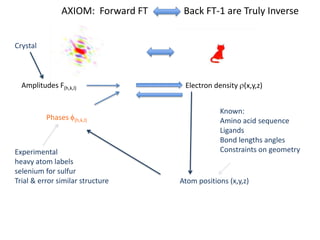
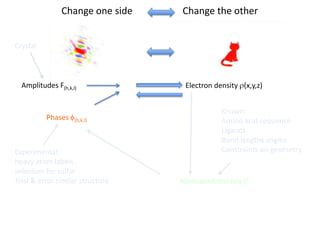
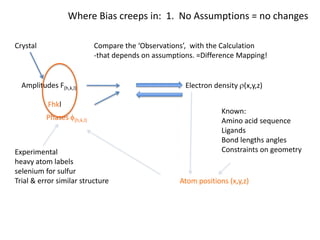
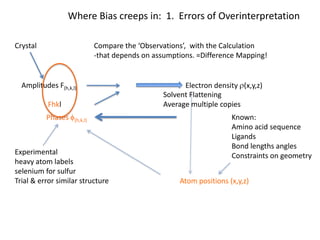
This document provides resources and an overview of topics for a course on crystallography and protein structure determination using X-ray crystallography. The course will involve crystallizing a protein, collecting data at the Advanced Light Source, and determining the protein's atomic structure. Key topics covered include X-ray scattering, the phase problem, structure refinement, and sources of errors. Online resources and contacts are provided for computing, tutorials, and beamline information.

1. B1 219 ROBERT M. STROUDUnderstanding crystallography and structuresInteractive – Bring conundra –Laboratory course: Crystallize a proteinDetermine structureVisit ‘Advanced Light Source’ (ALS) for data

2. Determining Atomic StructureX-ray crystallography = optics l ~ 1.5Å (no lenses)Bond lengths ~1.4ÅElectrons scatter X-rays; ERGO X-rays ‘see electrons’Resolution –Best is l/2 Typical is 1 to 3 ÅAccuracy of atom center positions ±1/10 Resolution 2q

3. Where do X-rays come from?=accelerating or decelerating electrons

4. Resources:http://www.msg.ucsf.eduComputingCalculation software-all you will ever needOn line course for some items:http://www-structmed.cimr.cam.ac.uk/course.htmlDr Chris Waddling msg.ucsf.eduDr James Holton UCSF/LBNLCrystallography accessible to no prior knowledge of the field or its mathematical basis. The most comprehensive and concise reference Rhodes' uses visual and geometric models to help readers understand the basis of x-ray crystallography.http://bl831.als.lbl.gov/~jamesh/movies/

5. Optical image formation, - without lenses

6. TopicsSummmary: Resources1 Crystal lattice optical analogues photons as waves/particles2 Wave addition complex exponential3. Argand diagramRepetition ==sampling fringe function5. Molecular Fourier Transform Fourier Inversion theorem sampling the transform as a product6. Geometry of diffraction7. The Phase problem heavy atom Multiple Isomorphous Replacement) MIR Anomalous Dispersion Multi wavelength Anomalous Diffraction MAD/SAD8. Difference Maps and Errors9. Structure (= phase) Refinement Thermal factors Least squares Maximum likelihood methods10. Symmetry –basis, consequences

7. Topics11. X-ray sources: Storage rings, Free Electron Laser (FELS)12. Detector systems13. Errors, and BIG ERRORS! –RETRACTIONS14. Sources of disorder15. X-ray sources: Storage rings, Free Electron Laser (FELS)

8. The UCSF beamline 8.3.1UCSF mission bayIf automated- why are there errors? What do I trust? Examples of errors trace sequence backwards,mis assignment of helicesetc

9. NH3 sites and the role of D160 at 1.35Å Resolution

10. Data/Parameter ratio is the same for all molecular sizes at the same resolution dminie. quality is the same!30S50S

11. Macromolecular StructuresGrowth in number and complexity of structures versus time

12. The universe of protein structures: Our knowledge about protein structures is increasing..65,271 protein structures are deposited in PDB (2/15/2010).This number is growing by > ~7000 a year Growing input from Structural Genomics HT structure determination (>1000 structures a year)

13. X-Ray Crystallography for Structure DeterminationGoals: 1. How does it work2. Understand how to judge where errors may lurk3. Understand what is implied, contained in the Protein Data Bank PDB http://www.pdb.org/pdb/home/home.doResolution: - suspect at resolutions >3 ÅR factor, and Rfree: statistical ‘holdout test’Wavelength ~ atom sizeScattering from electrons = electron densityAdding atoms? howObservations Intensity I(h,k,l) = F(hkl).F*(hkl)Determine phases y(hkl)Inverse Fourier Transform === electron densityJudging electron density- How to interpret?Accuracy versus Reliability

14. A Typical X-ray diffraction pattern~100 microns

15. qmax=22.5° if l=1ÅResolution1.35Å2qmax=45°

16. The Process is re-iterative, and should converge-but only so far!CrystalIntensities I(h,k,l)Electron density r(x,y,z)calculated I(h,k,l)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

17. Resolution dmin = l /2 sin (qmax)differs from Rayleigh criterion dmin = l /2 sin (qmax) is the wavelength of the shortest wave used to construct the density map

18. The Rayleigh CriterionThe Rayleigh criterion is the generally accepted criterion for the minimum resolvable detail - the imaging process is said to be diffraction-limited when the first diffraction minimum of the image of one source point coincides with the maximum of another. compared withsin (qmax) = l /2 dmin

19. How do we judge the Quality of structure?2. Overall quality criteria: agreement of observations with diffraction calculated from the interpreted structure.3. Since we refine the structureTo match the Ihkloverfitting ?Define Rfree for a ‘hold-out ‘ set of observations.4. OK? R < 20%, R free< 25%5. But the experimental errors in measuring Fo are ~ 3%.inadequate models of solvent, atom motion, anharmonicisity6 Accuracy ~ 0.5*res*R

20. Crystal lattice is made up of many ‘Unit Cells’Unit cell dimensions are 3 distances a,b,c and angles between them a,b,ghA ‘section’ throughScattering patternof a crystal l=0Note symmetry,Absences for h=even k=evenkCauses Sampling in ‘scattering space’Repetition in ‘Real space’

21. Crystal lattice is made up of many ‘Unit Cells’Unit cell dimensions are 3 distances a,b,c and angles between them a,b,ghVabc = |a.(bxc)|Vabc = |b.(cxa)|Vabc = |c.(axb)|kCauses Sampling in ‘scattering space’Repetition in ‘Real space’

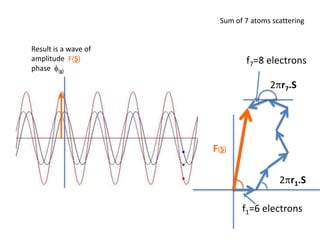
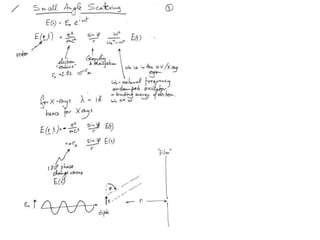
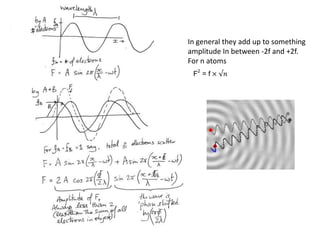
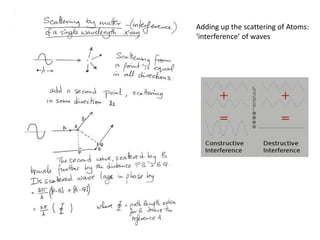
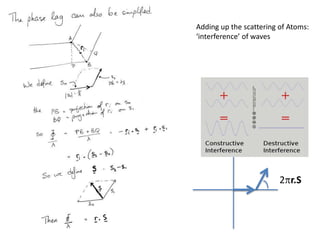
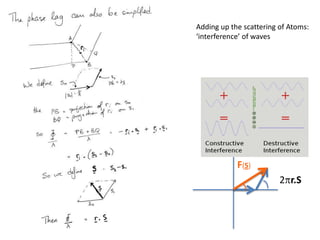
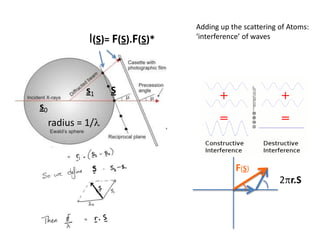
22. ScatteringAdding up the scattering of Atoms:‘interference’ of wavesWaves add out of phaseby 2p[extra path/l]

23. In general they add up to somethingamplitude In between -2f and +2f.For n atoms

24. Just 2 atoms…

25. Many atoms add by the same rules.Different in every direction.

26. Summary of the Process from beginningto structure..

27. Optical Equivalent: eg slide projector; leave out the lens..Optical diffraction = X-ray diffractionobjectImage of the objectobjectRemove the lens= observe scatteringpatternfilmobjectobject

29. ScatteringAdding up the scattering of Atoms:‘interference’ of waves

30. vectors revisited…Vectors have magnitude and directionPosition in a unit cellr = xa + yb + zcwhere a, b, c are vectors, x,y,z are scalars 0<x<1a.b = a b cos (q) projection of a onto b -called ‘dot product’axb = a b sin (q) a vector perpendicular to a, and b proportional to area in magnitude -- called cross productvolume of unit cell = (axb).c = (bxc).a = (cxa).b = -(bxa).c = -(cxb).a additivity: a + b = b + aif r = xa + yb + zc and s = ha* + kb* + lc* thenr.s = (xa + yb + zc).(ha* + kb* + lc* ) = xha.a* + xka.b* + xla.c* +yhb.a* + ykb.b* + ylb.c* + zhc.a* +zhc.a* + zkc.b* + zlc.c*as we will see, the components of the reciprocal lattive can be represented in terms of a* + b* + c*, where a.a* = 1, b.b*=1, c.c*=1 and a.b*=0, a.c*=0 etc..r.s = (xa + yb + zc ).(ha* + kb* + lc* ) = xha.a* + xka.b* + xla.c* +yhb.a* + ykb.b* + ylb.c* + zhc.a* +zhc.a* + zkc.b* + zlc.c*= xh + yk + zl

31. Adding up the scattering of Atoms:‘interference’ of waves2pr.S

32. Adding up the scattering of Atoms:‘interference’ of wavesF(S)2pr.S

33. Revisit..

38. Revision notes on McClaurin’stheorem. It allows any function f(x) to be definedin terms of its value at some x=a valueie f(a), and derivatives of f(x) at x=a,namely f’(a), f’’(a), f’’’(a) etc

41. Extra Notes on Complex Numbers(p25-28)

45. Wave representation

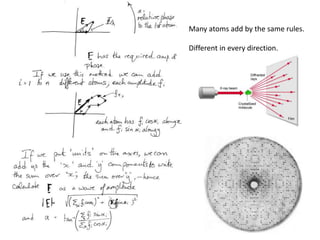
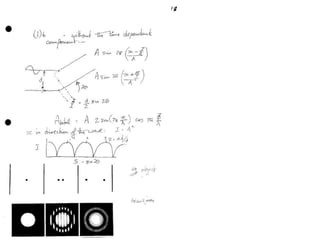
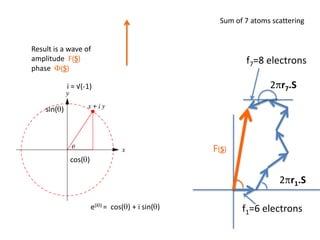
46. Argand Diagram.. F(S) = |F(s)| eiqIntensity = |F(s)|2How to represent I(s)?I(s) = |F(s)|2 =F(S) .F*(S) proof?Where F*(S) is defined to be the ‘complex conjugate’ of F(S) = |F(s)| e-iqso |F(s)|2 =|F(s)|[cos(q) + isin(q)].|F(s)|[cos(q) - isin(q)]=|F(s)|2 [cos2 (q) + sin2 (q)]=|F(s)|2 R.T.P.F(S)2pr.Sq

47. F*(S) is the complex conjugate of F(S), = |F(s)| e-iq(c+is)(c-is)=cos2q -cqisq+ cqisq+ sin2qso |F(s)|2 =F(S) .F*(S) -2pr.S-qF*(S)

49. Origin Position is arbitrary..proof..So the origin is chosen by choice of:a) conventional choice in each space group-eg Often on a major symmetry axis- BUT for strong reasons—see ‘symmetry section’.Even so there are typically 4 equivalent major symmetry axes per unit cell.. b) chosen when we fix the first heavy metal (or Selenium) atom position, -all becomes relative to that.c) chosen when we place a similar moleculefor ‘molecular replacement’ = trial and errorsolution assuming similarity in structure.

50. Adding waves from j atoms…F(S)= G(s) =

51. and why do we care?How much difference will it make to the average intensity? average amplitude?if we add a single Hg atom?

52. The ‘Random Walk’ problem? (p33.1-33.3)What is the average sum of n steps in random directions?(What is the average amplitude<|F(s)|> from an n atom structure?)-AND why do we care?!........How much difference from adding amercury atom (f=80).

53. The average intensity for ann atom structure, each of f electronsis <I>= nf2The average amplitude is Square rootof n, times f

54. and why do we care?How much difference will 10 electrons make to the average intensity? average amplitude?average difference in amplitude?average difference in intensity?if we add a single Hg atom?

55. and why do we care?How much difference will 10 electrons make to the average intensity? 98,000 e2average amplitude? 313average difference in amplitude?average difference in intensity?if we add a single Hg atom?

56. and why do we care?How much difference will 10 electrons make to the average intensity? 98,000 e2average amplitude? 313 eaverage difference in amplitude?2.2% of each amplitude!average difference in intensity?98,100-98000=100 (1%)if we add a single Hg atom?

57. and why do we care?or Hg atom n=80eHow much difference will 80 electrons make to the average intensity? 98,000 e2average amplitude? 313 eaverage difference in amplitude?18 % of each amplitude!average difference in intensity?104,400-98000=6400 (6.5%)

59. WILSON STATISTICSWhat is the expectedintensity of scattering versus the observedfor proteins of i atoms,?on average versus resolution |s|?

61. Bottom Lines:This plot should provide The overall scale factor(to intercept at y=1)The overall B factorIn practice for proteins it has bumpsin it, they correspond to predominantor strong repeat distances in the protein.For proteins these are at 6Å (helices)3Å (sheets), and 1.4Å (bonded atoms)

62. Topic: Building up a Crystal1 DimensionScattering from an array of points, is the same as scattering from one point,SAMPLED at distances ‘inverse’ to the repeat distance in the object The fringe functionScattering from an array of objects, is the same as scattering from one object,SAMPLED at distances ‘inverse’ to the repeat distance in the object eg DNA

63. Scattering from a molecule is described byF(s)= Si fi e(2pir.s)

68. Consequences of being a crystal?Repetition = sampling of F(S)34Å1/34Å-1

69. 2/lObject repeated 1/l

71. Consequences of being a crystal?Sampling DNA = repeating of F(S)1/3.4Å-13.4Å34Å1/34Å-1

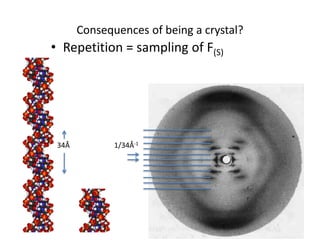
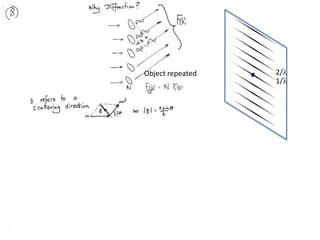
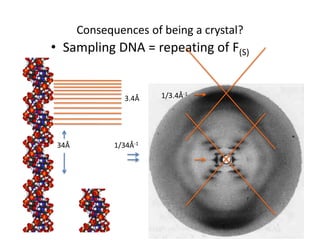
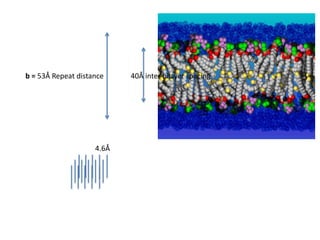
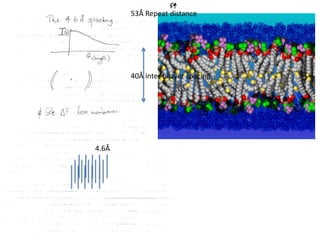
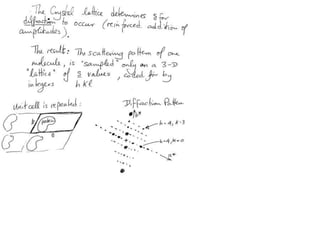
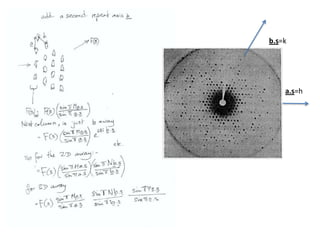
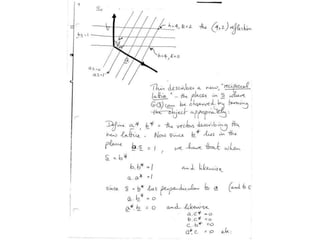
73. Transform of two hoizontal lines defined y= ± y1F(s) = Int [x=0-infexp{2pi(xa+y1b).s} + exp{2pi(xa-y1b).s}dVr ]=2 cos (2py1b).s * Int [x=0-infexp{2pi(xa).s dVr]for a.s=0 the int[x=0-infexp{2pi(xa).s dVr] = total e content of the linefor a.s≠0 int[x=0-infexp{2pi(xa).s dVr] = 0hence r(r)isa line at a.s= 0 parallel to b, with F(s) = 2 cos (2py1b).s -along a vertical line perpendicular to the horizontal lines.This structure repeats along the b direction thus peaks occur at b.s= k (where k is integer only)Transform of a bilayer..b=53Å

74. b = 53Å Repeat distance40Å inter bilayer spacing4.6Å

75. 53Å Repeat distance40Å inter bilayer spacing4.6Å

76. The Transform of a Molecule

78. How to calculate electron density?Proof of the Inverse Fourier Transform:

81. Definitions:

83. Build up a crystal from Molecules…First 1 dimension,a direction

89. b.s=ka.s=h

90. hkl=(11,5,0)Measure I(hkl)F(hkl)= √I(hkl)Determine f(s) = f(hkl)Calculate electron density map

92. The density map is made up of interfering density waves through the entire unit cell…

93. Geometry of Diffraction

95. A Typical X-ray diffraction pattern~100 microns

100. A Typical X-ray diffraction pattern~100 microns

104. l=2dhklsin(q)

108. Compute a Transform of a series of 50%b/50%w parallel linesRonchi ruling:

111. This is all there is? YES!!Scattering pattern is the Fourier transform of the structure FTF(S) = Sjfj e(2pirj.S)FT-1Structure is the ‘inverse’Fourier transform of the Scattering pattern 1/ar(r) = SF(S) e(-2pir.S)aFTb1/bFT-1

112. But we observe |F(S)|2 and there are ‘Phases’Scattering pattern is the Fourier transform of the structure FTF(S) = Sjfj e(2pirj.S)FT-1Structure is the ‘inverse’Fourier transform of the Scattering pattern 1/ar(r) = SF(S) e(-2pir.S)aFTWhere F(S) has phaseAnd amplitude b1/bFT-1

113. This is all there is?Scattering pattern is the Fourier transform of the structure FTF(S) = Sjfj e(2pirj.S)SFT-1Structure is the ‘inverse’Fourier transform of the Scattering pattern 1/ar(r) = SF(S) e(-2pir.S)aFTbF(h,k,l) = Sjfj e(2pi(hx+ky+lz))S1/bh=15, k=3,r(x,y,z) = SF(h,k,l) e(-2pir.S)FT-1

114. Relative Information in Intensities versus phasesr(r) duckr(r) cat|F(S)|F(S)= Sjfj e(2pirj.S)F(S) duckF(S) catf(s)|F(S)|duckr(r) = SF(S) e(-2pir.S)f(s) catLooks like a …..

115. Relative Information in Intensities versus phasesr(r) duckr(r) cat|F(S)|F(S)= Sjfj e(2pirj.S)F(S) duckF(S) catf(s)|F(S)|duckr(r) = SF(S) e(-2pir.S)f(s) catLooks like a CATPHASES DOMINATE:-Incorrect phases = incorrect structure-incorrect model = incorrect structure-incorrect assumption = incorrect structure

116. Measure I(hkl)

117. The Process is re-iterative, and should converge-but only so far!CrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

118. Phase determination by any means, ends up as a probabilty distribution. So Fh,k,l, f(h,k,l)Then what to use for the best map?r(r) = SF(S) e(-2pir.S) ?the signal towards some F true will beIntegral P(F(S)) cos (f(h,k,l) –ftrue)and the ‘noise ‘ will be Integral P(F(S)) sin (f(h,k,l) –ftrue)The map with the least noise will haveF(s) = center of mass of P(F(S))

119. Phase determination by any means, ends up as a probabilty distribution. So Fh,k,l, f(h,k,l)Then what to use for the best map?r(r)best= F(S) e(-2pir.S) ?The map with the least noise will haveF(s) = center of mass of P(F(S))= Int P F sin(f-f(best)) is a minimum. Then m = Int P F cos(f-f(best))/Fiem|F(s)| f(best) =Int P.Fwhere m = figure of merit = Int P(F) F(s) noise = Int F(s) sin

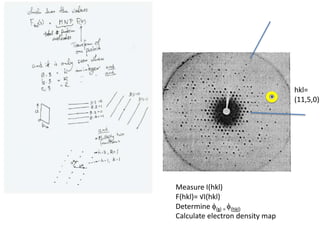
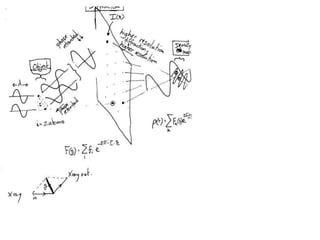
120. If a map is produced with some f(hkl)The probability of it being correct is P(hkl)P(hkl) (f(hkl))Maximum value of P(hkl) (f(hkl)) gives the ‘Most probable’ mapMap with the least mean square error, is when noise is minimum, Int find f(best) such that Q= Intf [|F| P(hkl) (f(hkl))exp (if(hkl)) - Fbestf(best))]2df is minimum.is minimum when dQ/dFbest= 0so Fbestf(best) = f |F| P(hkl) (f(hkl))exp (if(hkl))dfFbestf(best) = m|F| center of ‘mass’ of the Probability distribution m = IntP(hkl) (f(hkl))cos(f - f(best))consider errors from one reflection, and its complex conjugate<(Dr)2> = 2/V2 Then F= IntFcos(f - f(best))/ FNoise = 1/V Int F sin (f - f(best))/F = F(1-m2)mF where

121. s0sssAdding up the scattering of Atoms:‘interference’ of wavesI(S)= F(S).F(S)*s1Ss0radius = 1/lF(S)2pr.S

122. How to be ‘UNBIASED’ The Observations are constant F(hkl)The phases change according to presumptions..Remove all assumptions about any questionable region as early as possibleRe-enforce the observations at each cycle and try to improve the phases without biasIt is an objective method (prone to human aggressive enthusiasm.

123. AXIOM: Forward FT Back FT-1 are Truly InverseCrystalAmplitudes F(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

124. Change one side Change the other CrystalAmplitudes F(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

125. Where Bias creeps in: 1. No Assumptions = no changes CrystalCompare the ‘Observations’, with the Calculation-that depends on assumptions. =Difference Mapping!Amplitudes F(h,k,l)Electron density r(x,y,z)FhklKnown:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

126. Where Bias creeps in: 1. Errors of OverinterpretationCrystalCompare the ‘Observations’, with the Calculation-that depends on assumptions. =Difference Mapping!Amplitudes F(h,k,l)Electron density r(x,y,z)Solvent FlatteningAverage multiple copiesFhklPhases f(h,k,l)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryExperimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

127. A reminder: Each individual F(hkl) has its own Phase F(hkl)Result is a wave of amplitude |F(S)|phase F(S)Sum of 7 atoms scattering2pr7.Si = √(-1)sin(q)F(S)cos(q)F(S)2pr1.Sf1=6 electronse(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

128. Suppose we interpret 7 atoms; but 3 remain to be found in densityResult is a wave of amplitude |F(S)|phase F(S)In reality, maybe 3 atoms are missing.How to see what is missing?2pr7.Si = √(-1)Sum of 7 atoms scatteringsin(q)F(S)cos(q)2pr1.Sf1=6 electronse(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

129. Observed F(hkl) will contain a part of that information..Sum of 7 atoms scatteringResult is a wave of amplitude |F(S)|phase F(S)In reality, maybe 3 atoms are missing.How to see what is missing?|F(S)|observed2pr7.Si = √(-1)sin(q)F(S)cos(q)phase F(S)2pr1.Sf1=6 electronse(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

130. In reality The missing component isThe Difference F(S) obs- F(S)calcIt has all the missing information.Transform it= all missing parts.But all we know is |F(S)|observed|F(S)|calcand current (biased) phase F(S)So what if we take the Difference weknow||F(S)|obs- |F(S)|calc| and F(S)In reality, maybe 3 atoms are missing.How to see what is missing?|F(S)|observed2pr7.SF(S)2pr1.Sphase F(S)e(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

131. The BEST WE CAN DO…IS DF, F(S)It contains a component of the truth DF cos(q), and an error component DF sin(q)In reality The missing component isThe Difference F(S) obs- F(S)calcIt has all the missing information.Transform it= all missing parts.But all we know is |F(S)|observed|F(S)|calcand current (biased) phase F(S)So what if we take the Difference weknow||F(S)|obs- |F(S)|calc| and F(S)= DF and F(S)cos(q)|F(S)|observed2pr7.SDFqF(S)2pr1.Sphase F(S)e(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

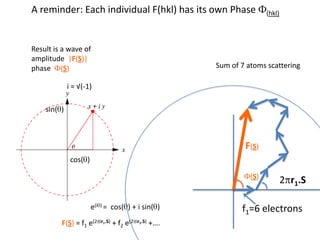
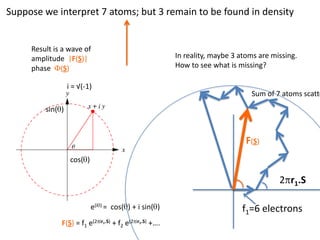
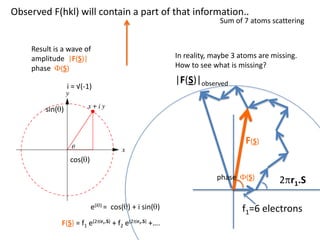
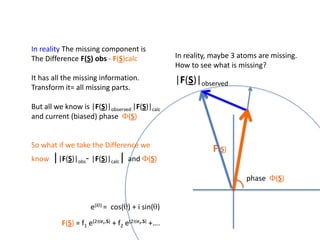
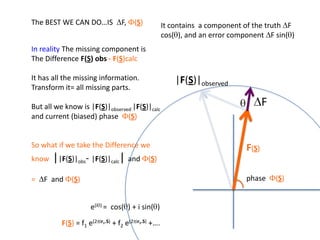
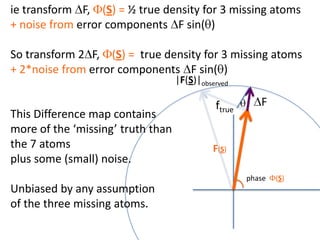
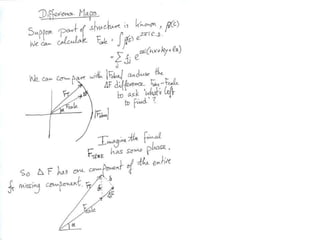
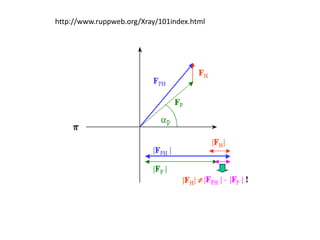
132. What contribution to the ‘missing truth’?It contains a component of the truth DF cos(q)and an error component DF sin(q)So what if we transform the Difference weknowDF =||F(S)|obs- |F(S)|calc| and F(S)On average DF = ftruecos(q)so On average towards the truth isDF cos(q) = ftruecos2(q)What is the average value of cos2(q)?= ½ ( cos 2q +1)cos(q)|F(S)|observed2pr7.SDFqftrueF(S)p/2+ 1dq/ 1/2p/22pr1.Sp/2= ½ 0[ -f sin2q + q]/= ½ fie transform DF, F(S) = ½ true density for 3 missing atomsphase F(S)p/2e(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

133. It contains a component of the truth DF cos(q)and an error component DF sin(q)So what if we transform the Difference weknowDF =||F(S)|obs- |F(S)|calc| and F(S)On average DF = ftruecos(q)so On average towards the truth isDF cos(q) = ftruecos2(q)Since the average value of cos2(q)= cos(q)|F(S)|observed2pr7.SDFqftrueF(S)2pr1.S= ½ fie transform DF, F(S) = ½ true density for 3 missing atoms+ noise from error components DF sin(q)phase F(S)e(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

134. ie transform DF, F(S) = ½ true density for 3 missing atoms+ noise from error components DF sin(q)So transform 2DF, F(S) = true density for 3 missing atoms+ 2*noise from error components DF sin(q)This Difference map containsmore of the ‘missing’ truth than the 7 atomsplus some (small) noise.Unbiased by any assumptionof the three missing atoms.cos(q)|F(S)|observed2pr7.SDFqftrueF(S)2pr1.Sphase F(S)e(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

135. USES: 1. Finding the missing parts of a model.The Transform of |F(S)|calcF(S) = 7 atoms assumed2DF F(S) = density for 3 missing atoms + ‘noise’(|F(S)|calc + 2DF) F(S) = all 10 atomsSinceDF =||F(S)|obs- |F(S)|calc| this is2|F(S)|obs- |F(S)|calccalled a ‘2F0-Fc map’cos(q)|F(S)|observed2pr7.SDFqftrueF(S)It is unbiased as to where the missingcomponents are2pr1.Sphase F(S)e(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

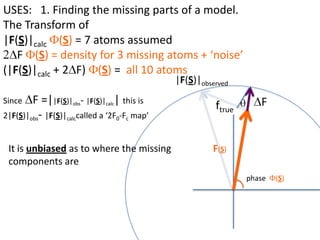
136. USES: 2. Add a substrate, Grow a new crystalMeasure New |F(S)|obs+substrateCompare with the apo-protein.TransformDF =||F(S)|obs+substrate- |F(S)|obs|F(S)or[2|F(S)|obs+substrate- |F(S)|obs ] F(S)= a ‘2F0-Fo map’cos(q)|F(S)|observed2pr7.SDFqftrueF(S)It is unbiased as to where the missingsubstrate is.2pr1.Sphase F(S)e(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

137. Difference Maps: Errors and Signal

142. Fo-Fc maps identify everything ordered that is 'missing'mapmap-Eliminate Bias-Half electron content-See electrons

143. Probability, Figure of merit, and the Heavy atom method of Phase Determination.

145. http://www.ruppweb.org/Xray/101index.html

163. Difference Maps: Errors and Signal

167. The Best Fourier: Minimizing errors in the density map.

168. Seeing Single electrons:Errors in Difference maps are much smaller than in protein maps.Dr ~ |DF0|/Volume of unit cell versusDr ~ |F0|/Volume of unit cell Peaks of atoms are seen in less and less noise as refinement progresses.(rms errors)1/2~ |DF0| Thus errors in|F(Protein+Substrate)| - |F(Protein)| areby far lower (like Rmerge ~5%Fo) than for |Fo-Fc| (like Rfactor~20% of FoCan easily see movement of <1/10resolution (<0.2Å)

170. A Dfference map shows 1/3 occupied NH3 sites and the role of D160 at 1.35Å Resolution. Here are 0.3 NH3 peaks!Khademi..Stoud 2003

171. Fo-Fc maps identify everything ordered that is 'missing'mapmap-Eliminate Bias-Half electron content-See electrons

172. The closer you get –the lower the noise. Can see single electrons!|2Fo-Fc| ac mapThe structure showing‘thermal ellipsoids’ at50% Probability|Fo-Fc| ac mapFigure 3 The catalytic triad. (A) Stereoview displaying Model H superimposed on the 2Fo Fc (model H phases) at 1 (aqua) and 4 (gold). The densities for C and N in His 64 are weaker than in Asp 32. The Asp 32 CO2 bond at 4 is continuous, while the density for the C and O1 are resolved. (B) Schematic of the catalytic residues and hydrogen bonded neighbors with thermal ellipsoid representation countered at 50% probability (29). Catalytic triad residues Ser 221 and His 64 show larger thermal motion than the Asp 32. Solvent O1059 appears to be a relatively rigid and integral part of the enzyme structure. (C) Catalytic hydrogen bond (CHB). A FoFc (model H phases) difference map contoured at +2.5 (yellow) and 2.5 (red) and a 2Fo Fc (model H phases) electron density map contoured at 4 (gold). The position of the short hydrogen atom (labeled HCHB) in the CHB is positioned in the positive electron density present between His 64 N1 and Asp 32 O2.Published in: Peter Kuhn; Mark Knapp; S. Michael Soltis; Grant Ganshaw; Michael Thoene; Richard Bott; Biochemistry 1998, 37, 13446-13452.DOI: 10.1021/bi9813983Copyright © 1998 American Chemical Society4/11/11

173. Seeing small shifts-down to ±0.1ÅDifference Mapnoise ~20% of noise in the parent protein-and only two peaks!

174. 2Fo-Fc maps (aqua and gold)Fo-Fc map in yellow and purple show individual hydrogen atoms!Figure 2 (A) Electron density for Asp 60. Fo Fc difference electron density map, contoured at +2.5 (yellow) and 2.5 (purple), is superimposed on a 2Fo Fc electron density map contoured at 1 (aqua) and 4 (gold), based on model H (Table 2). No hydrogen atoms were included for residues Asp 60, Gly 63, Thr 66, and solvent. At the 4 contour, the electron density between C and both O1 and O2 are equivalent as expected. (B) H2O hydrogen bonding in an internal water channel. Electron density; 2Fo Fc (model H phases) contoured at 4 (gold) level is superposed on Fo Fc (model H phases) difference electron density contoured at +2.5 (yellow) and 2.5 (purple) level. Peaks for both hydrogen atoms on solvent O1024 are seen along with hydrogen atoms of neighboring solvent and Thr 71 O1. A zigzag pattern of alternating proton donors and acceptors can be seen extending from Thr 71 O1 in the interior, through a chain of four solvent molecules ending at the surface of the enzyme (Figure 1). Published in: Peter Kuhn; Mark Knapp; S. Michael Soltis; Grant Ganshaw; Michael Thoene; Richard Bott; Biochemistry 1998, 37, 13446-13452.DOI: 10.1021/bi9813983Copyright © 1998 American Chemical Society4/11/11

178. What happens if we transform what we do know and can measure, namely I(S) = |F(S)|observedP(r) = S|F(S)|2e(-2pir.S)

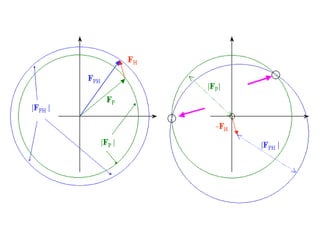
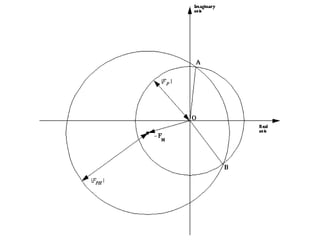
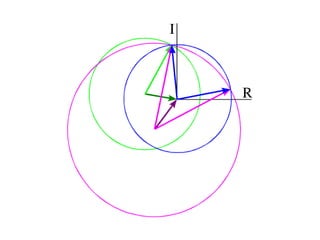
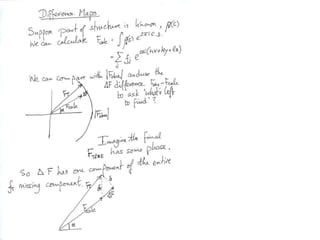
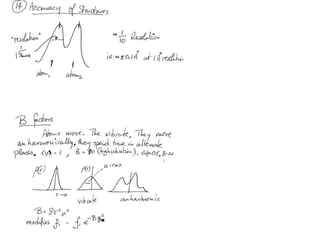
179. Transform of I(hkl) = Transform of F2(hkl)…What happens if I transform what I do know and can measure, namely I(S) = |F(S)|observedieP(r) = S|F(S)|2e(-2pir.S)= S [F(S).F*(S)]e(-2pir.S) ?

182. Arthur Lindo Patterson (1902-1966), innovative crystallographer who devised the well-known Patterson method (Patterson function) used in crystal-structure determination.

184. Molecular Replacement

185. Patterson map

186. Intramolecular vectors before rotation

187. Colour-coded Patterson map

188. Intramolecular vectors after rotation

189. All vectors brought to a common origin.20eConsider a structure of 2 atomsone 20 electrons, one 30 electrons-in a monoclinic ‘space group’ie. a two fold symmetry axis is present, symbolized by 30eba

190. 2*

191. 2*

192. 2*

193. 2*

194. 2*

197. Problem Set: Interpret a Patterson mapin terms of heavy mercury atompositions

201. Density Modification- and Density Averaging.

202. The Process is re-iterative, and should converge-but only so far!CrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

203. The Process is re-iterative, and should converge-but only so far!CrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

204. The Process is re-iterative, and should converge-but only so far!CrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

205. Density Modification: Solvent FlatteningCrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

206. Density Modification: Place expected atomsCrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

207. Density Modification: Non-Crystal SymmetryCrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

208. Density Modification: Non-Crystal SymmetryCrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

209. Density Modification: Non-Crystal SymmetryCrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

221. Addendum on Icosohedral virus structures

223. Triangulation numbers of icosohedral virusesThere are 60T copies of each protein (asymmetric unit) in the capsid.T=h2 + k2 + hkwhere h, k are integersT=1,3,4,7,9,12,13, 16, 21,25are all possible.

228. Sum of 7 atoms scatteringResult is a wave of amplitude F(S)phase f(s) f7=8 electrons2pr7.SF(S)2pr1.Sf1=6 electrons

229. Sum of 7 atoms scatteringResult is a wave of amplitude F(S)phase F(S)f7=8 electrons2pr7.Si = √(-1)sin(q)F(S)cos(q)2pr1.Sf1=6 electronse(iq) = cos(q) + isin(q)

230. Sum of 7 atoms scatteringResult is a wave of amplitude |F(S)|phase F(S)f7=8 electrons2pr7.Si = √(-1)sin(q)F(S)cos(q)2pr1.Sf1=6 electronse(iq) = cos(q) + isin(q)F(S) = f1 e(2pir1.S) + f2 e(2pir2.S) +….

231. Sum of 7 atoms scatteringResult is a wave of amplitude |F(S)|phase F(S)f7=8 electrons2pr7.Si = √(-1)sin(q)F(S)cos(q)2pr1.Sf1=6 electronse(iq) = cos(q) + isin(q)F(S) = Sjfj e(2pirj.S)

232. Sum of 7 atoms scatteringf7=8 electrons2pr7.SF(S)2pr1.Sf1=6 electrons

233. f7=8 electrons2pr7.SF(S)2pr1.Sf1=6 electrons

234. e(iq) = cos(q) + isin(q)F(S) = Sjfj e(2pirj.S)

235. The Process is re-iterative, and should converge-but only so far!CrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

236. Scattering pattern is the Fourier transform of the structure F(S) = Sjfj e(2pirj.S)Structure is the ‘inverse’Fourier transform of the Scattering pattern r(r) = SF(S) e(-2pir.S)

244. Rosalind Franklin and DNA

249. Consequences of being a crystal?Repetition = sampling of F(S)34Å

250. Consequences of being a crystal?Repetition = sampling of F(S)34Å1/34Å-1

251. 2/lObject repeated 1/l

253. Build a crystalObjectScattering

254. Early Definitions:

258. a.s=hb.s=k

259. hkl=(11,5,0)Measure I(hkl)F(hkl)= √I(hkl)Determine f(s) = f(hkl)Calculate electron density map

261. The density map is made up of interfering density waves through the entire unit cell…

262. Appendix: Slides for recall

263. The Process is re-iterative, and should converge-but only so far!CrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

264. The Process is re-iterative, and should converge-but only so far!CrystalIntensities I(h,k,l)Electron density r(x,y,z)Known:Amino acid sequenceLigandsBond lengths anglesConstraints on geometryPhases f(h,k,l)Experimentalheavy atom labelsselenium for sulfurTrial & error similar structureAtom positions (x,y,z)

275. Anomalous Diffraction

277. ie Wavelength < absorption edge

279. Anomalous diffraction

280. Friedel’s Law: F(hkl)=F(-h,-k,-l)a(hkl)=-a F(-h,-k,-l)

281. http://www.ruppweb.org/Xray/101index.htmlfor any/all elements..

286. Anomalous scattering goes against Friedels Law. –Hence it can be used to break the ambiguity in phase from a single heavy metal derivative, --or to determine the phase of F(hkl)

287. The Phase probabilty diagram now chooses between the two choices for F(hkl) and F(-h,-k,-l) Paa

288. The Phase probabilty diagram now chooses between the two choices for F(hkl) and F(-h,-k,-l) Pa for F(hkl)amFomFo

289. And now for F(-h,-k,-l) Paa-amFomFoPhase Combination Pa (hkl) = P(hkl)ano. P(hkl)heavy atom 1. P(hkl)heavy atom 2….

290. And now for F(-h,-k,-l) PaamFomFoPhase Combination Pa (hkl) = P(hkl)ano. P(hkl)heavy atom 1. P(hkl)heavy atom 2….

293. RefinementLeast Squares Refinement is common when errors in observations are presumed to be random errors that obey Gaussian statistics.Refine xi,yi,zi, Bi with respect to the FoMinimize E = Shkl1/s2(k|Fobs|-|Fcalc|)2 with respect to (xyzB)i of all atoms.To include an energy term, that constrains the structure toward acceptable geometryMinimize E = (1-w) Energy + w Shkl1/s2(k|Fobs|-|Fcalc|)2 where w is the fractional weighting on geometry versus X-ray terms. Energy has vdW, torsional restraints, bond length and dihedral angles.Maximum Likelihood refinement seeks the most probable solution most consistent with all observations. ie Least squares refinement alone minimizes the difference between |Fo| and |Fc|, however

294. Principle of maximum likelihoodThe basic idea of maximum likelihood is quite simple: the best model is most consistent with the observations. Consistency is measured statistically, by the probability that the observations should have been made. If the model is changed to make the observations more probable, the likelihood goes up, indicating that the model is better. (You could also say that the model agrees better with the data, but bringing in the idea of probability defines "agreement" more precisely.) An example of likelihoodThe behaviour of a likelihood function will probably be easier to understand with an explicit example. To generate the data for this example, I generated a series of twenty numbers from a Gaussian probability distribution, with a mean of 5 and a standard deviation of 1. We can use these data to deduce the maximum likelihood estimates of the mean and standard deviation.

295. In the following figure, the Gaussian probability distribution is plotted for a mean of 5 and standard deviation of 1. The twenty vertical bars correspond to the twenty data points; the height of each bar represents the probability of that measurement, given the assumed mean and standard deviation. The likelihood function is the product of all those probabilities (heights). As you can see, none of the probabilities is particularly low, and they are highest in the centre of the distribution, which is most heavily populated by the data.

296. What happens if we change the assumed mean of the distribution? The following figure shows that, if we change the mean to 4, the data points on the high end of the distribution become very improbable, which will reduce the likelihood function significantly. Also, fewer of the data points are now in the peak region.

297. What happens if we have the correct mean but the wrong standard deviation? In the following figure, a value of 0.6 is used for the standard deviation. In the heavily populated centre, the probability values go up, but the values in the two tails go down even more, so that the overall value of the likelihood is reduced.

298. Similarly, if we choose too high a value for the standard deviation (two in the following figure), the probabilities in the tails go up, but the decrease in the heavily-populated centre means that the overall likelihood goes down. In fact, if we have the correct mean the likelihood function will generally balance out the influence of the sparsely-populated tails and the heavily-populated centre to give us the correct standard deviation.

299. We can carry out a likelihood calculation for all possible pairs of mean and standard deviation, shown in the following contour plot. As you see, the peak in this distribution is close to the mean and standard deviation that were used in generating the data from a Gaussian distribution.

300. Maximum Likelihood Refinement is better than ‘Least Squares Refinement’A simple ‘Least squares‘ approach assumes that all errors are ‘Gaussian’, and that errors are all in the AmplitidesFo. But they are not..To use the structure factor distributions to predict amplitudes, we have to average over all possible values of the phase, and this changes the nature of the error distributions. The rms error in the structure factors involves a vector difference, but we can turn our amplitude difference into a vector difference by assigning both amplitudes the calculated phase.