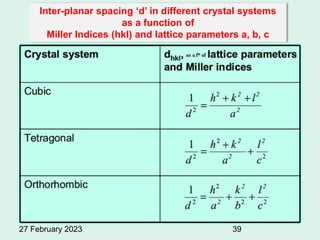
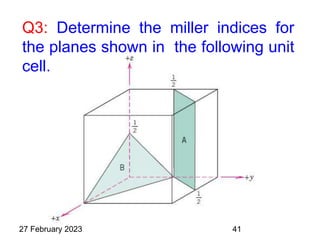
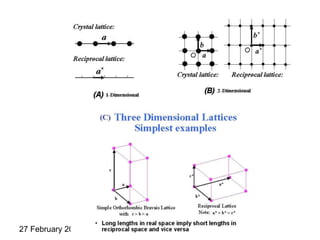
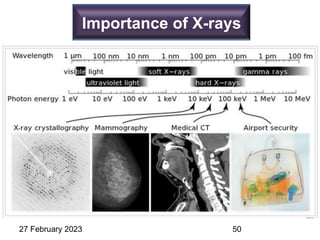
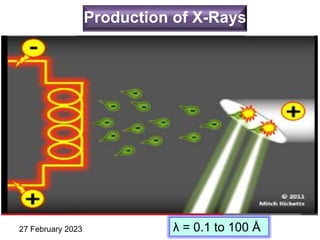
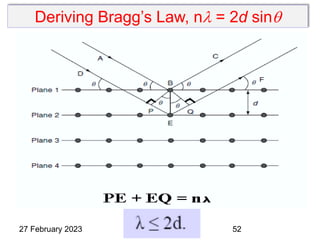
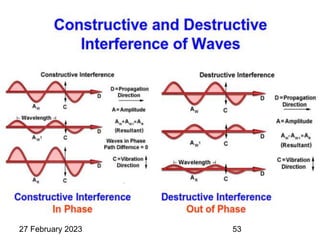
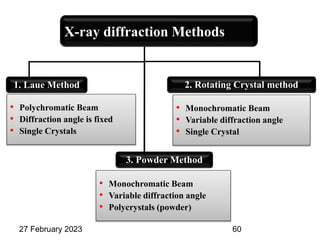
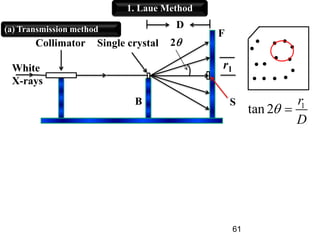
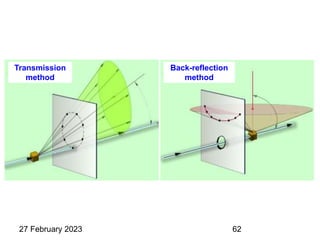
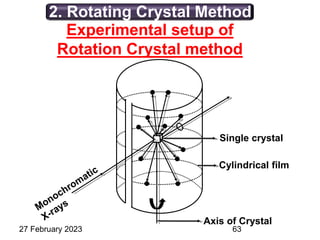
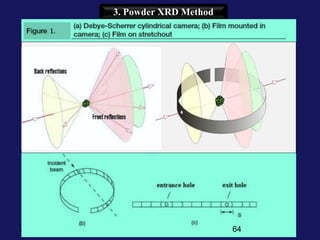
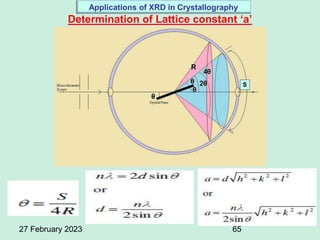
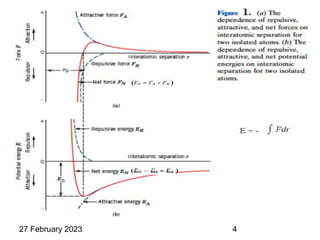
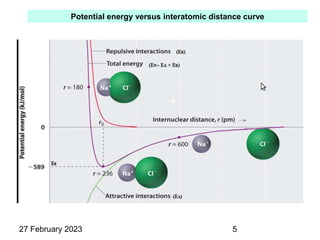
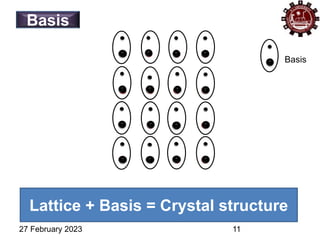
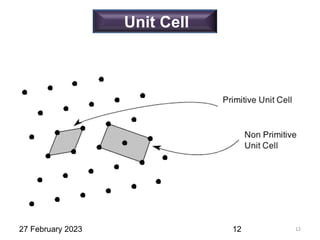
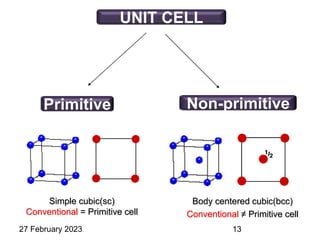
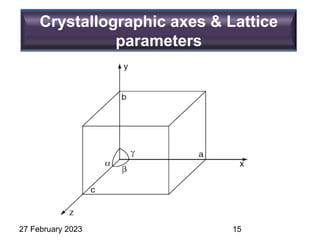
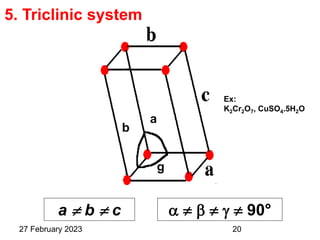
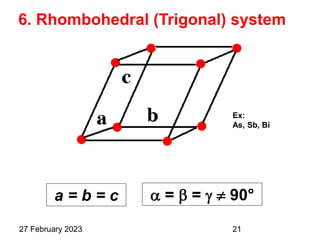
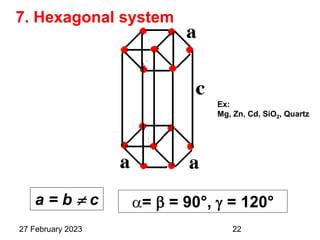
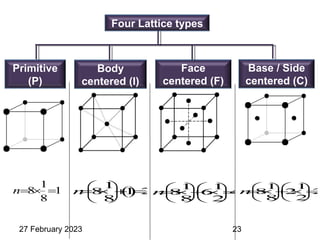
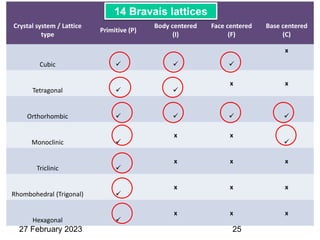
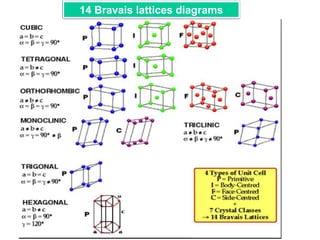
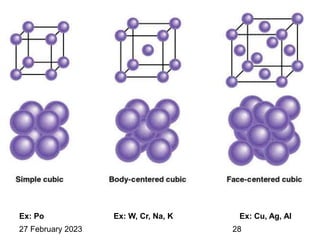
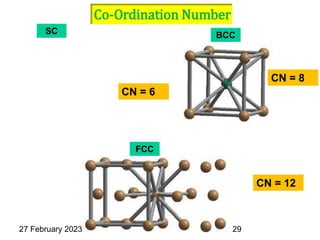
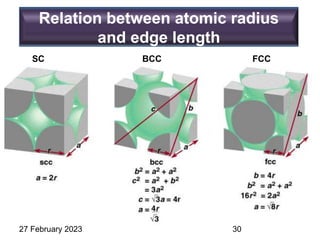
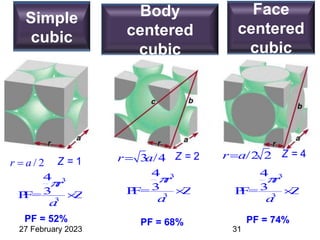
This document provides an overview of crystallography and bonding in solids. It discusses various types of interatomic bonds and classifications of materials, including crystals, quasicrystals, and amorphous solids. It also describes basic crystallographic concepts such as unit cells, Bravais lattices, crystal systems, Miller indices, and X-ray diffraction. Bragg's law for X-ray diffraction is derived. Different X-ray diffraction methods including Laue, rotating crystal, and powder methods are explained. Applications of X-ray diffraction in crystallography are also discussed.

1. Chapter 1
Crystallography
27 February 2023 1

2. Session 1
27 February 2023 2

3. Bonding in solids
Process of holding atoms together in solids is
called Bonding.
Intermolecular foreces are responsible for
holidng the atoms to stay together in materials.
The work done by these forces represents
potential energy.
The potential energy versus interatomic distance
relation is important for understanding properties
of solids.
27 February 2023 3

4. 27 February 2023 4

5. Potential energy versus interatomic distance curve
27 February 2023 5

6. 27 February 2023
Interatomic Bonds in Solids
Pimary Bonds
(Chemical Bonds)
Strong
Secondary Bonds
Weak
Ionic
Covalent
Metallic
Van der waal’s
Hydrozen
6

7. Classification of matter
Crystals
Qusicrystal
s
Amorphous
Single
Crystals
Polycrystals
27 February 2023

8. 27 February 2023 8

9. Basic Definitions
a
27 February 2023

10. Translation
vector
O
B 2a b
  
 
B
2 a

b

O x
y
a
b
27 February 2023
In 3-dimensions, in general,

11. Basis
Basis
Lattice + Basis = Crystal structure
27 February 2023 11

12. Unit Cell
12
27 February 2023 12

13. UNIT CELL
Primitive Non-primitive
Body centered cubic(bcc)
Conventional ≠ Primitive cell
Simple cubic(sc)
Conventional = Primitive cell
27 February 2023 13

14. Session 2
27 February 2023 14

15. Crystallographic axes & Lattice
parameters
27 February 2023 15

16. 1. Cubic Crystal System
a = b = c  =  =  = 90°
Seven Crystal Systems
Ex:
Cu, Ag, Au,
Diamond, NaCl
27 February 2023 16

17. 2.Tetragonal system
a = b  c  =  =  = 90°
Ex:
TiO2, NiSO4,
SnO2, KH2PO4
27 February 2023 17

18. 3. Orthorhombic system
 =  =  = 90°
a  b  c
Ex:
BaSO4, K2SO4, SnSO4,
PbCO3, KNO3
27 February 2023 18

19. 4. Monoclinic system

a  b  c  =  = 90°,   90°
Ex:
Gypsum (CaSO4.2H2O),
Cryolite (Na3AlF6),
FeSO4, Na2SO4
27 February 2023 19

20. a
b
g
5. Triclinic system
      90°
a  b  c
Ex:
K2Cr2O7, CuSO4.5H2O
27 February 2023 20

21.  =  =   90°
6. Rhombohedral (Trigonal) system
a = b = c
Ex:
As, Sb, Bi
27 February 2023 21

22. 7. Hexagonal system
a = b  c =  = 90°,  = 120°
Ex:
Mg, Zn, Cd, SiO2, Quartz
27 February 2023 22

23. Four Lattice types
Primitive
(P)
Body
centered (I)
Face
centered (F)
Base / Side
centered (C)
1
8 1
8
n   
1
8 1 2
8
n
 
   
 
 
1 1
8 6 4
8 2
n
  
  
  
  
1 1
8 2 2
8 2
n
  
  
  
  
27 February 2023 23

24. Bravais Lattice
 If the surroundings of each lattice point in a
space lattice is the same or if the atom or all
the atoms at lattice points are identical, then
such a lattice is called the Bravais lattice.
 On the other hand, If the surroundings of each
lattice point is not the same, then it is called
the Non-Bravais lattice.
 Originated from 7 Crystal systems and 4
lattice types, 14 Bravais lattices are possible
in 3-dimensional space.
27 February 2023 24

25. Crystal system / Lattice
type
Primitive (P)
Body centered
(I)
Face centered
(F)
Base centered
(C)
Cubic   
x
Tetragonal  
x x
Orthorhombic    
Monoclinic 
x x

Triclinic 
x x x
Rhombohedral (Trigonal) 
x x x
Hexagonal 
x x x
14 Bravais lattices
27 February 2023 25

26. 27 February 2023 26
14 Bravais lattices diagrams

27. Session 3
27 February 2023 27

28. 27 February 2023
Ex: Po Ex: W, Cr, Na, K Ex: Cu, Ag, Al
28

29. 27 February 2023
Co-Ordination Number
SC BCC
FCC
29
CN = 6
CN = 8
CN = 12

30. Relation between atomic radius
and edge length
27 February 2023
SC BCC FCC
30

31. Simple
cubic
Body
centered
cubic
Face
centered
cubic
3
3
4
3
P
F= Z
r
a


3
3
4
3
P
F= Z
r
a


3
3
4
3
P
F= Z
r
a


/ 2
r a
 Z = 1 3 /4
r a
 Z = 2 /2 2
r a
 Z = 4
PF = 52% PF = 68% PF = 74%
27 February 2023 31

32. 27 February 2023
Lattice constant ‘a’ in terms of
density of the crystal ‘ρ’
32
NA=
6.023 X 10
23

33. Session 4
27 February 2023 33

34. 27 February 2023
Crystal directions, Crystal planes
&
Miller Indices
Crystal directions
34

35. Different lattice planes in a crystal
d
27 February 2023
Crystal planes
35

36. Crystal Planes & Miller Indices
27 February 2023 36

37. 27 February 2023
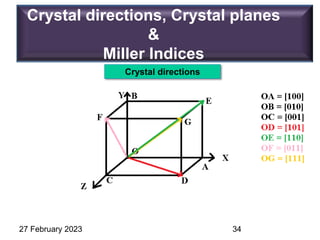
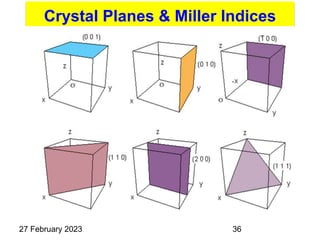
 [hkl] Direction, eg. [120]
 (hkl) Plane, eg. (101)
 <hkl> Family of equivalent directions, eg.
 {hkl} Family of equivalent planes, eg.
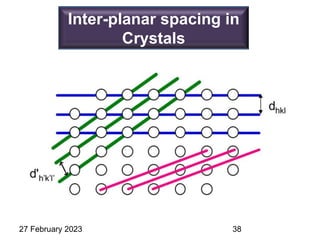
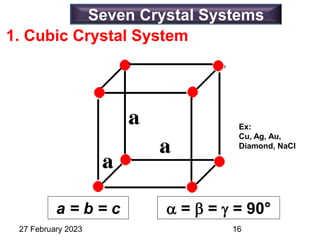
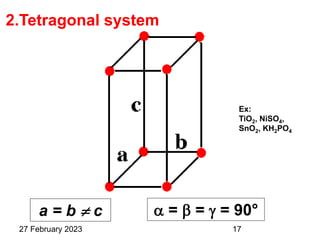
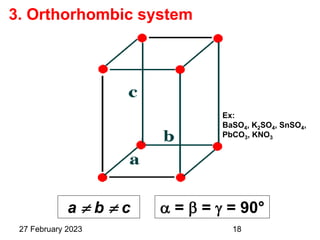
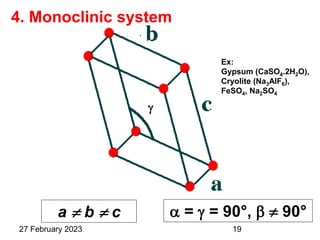
Representation of Crystal directions & Crystal planes
37

38. Inter-planar spacing in
Crystals
27 February 2023 38

39. Inter-planar spacing ‘d’ in different crystal systems
as a function of
Miller Indices (hkl) and lattice parameters a, b, c
27 February 2023 39

40. Q1:
Q2:
Problems on Miller indices
27 February 2023 40

41. Q3: Determine the miller indices for
the planes shown in the following unit
cell.
27 February 2023 41

42. Q4: What are Miller Indices? Draw (111) and
(110) planes in a cubic lattice.
Q5: Sketch the following planes of a cubic unit
cell (001), (120), (211).
Q6: Obtain the Miller indices of a plane which
has intercepts at a, b/2 and 3c in simple cubic
unit cell. Draw a neat diagram showing the
plane.
27 February 2023 42
Q7: In a crystal whose primitives are 1.2 Å, 1.8 Å
and 2.0 Å, a plane (231) cuts an intercept 1.2 Å on
X – axis. Find the corresponding arcs on the Y and
Z axes.

43. Problems on inter-planar
spacing
1. Explain how the X-ray diffraction can be
employed to determine the crystal
structure. Give the ratio of inter-planar
distances of (100), (110) and (111)
planes for a simple cubic structure.
27 February 2023 43

44. 2. The distance between (110) planes in
a body centered cubic structure is 0.203
nm. What is the size of the unit cell?
What is the radius of the atom?
27 February 2023 44

45. It is easy to think a set of parallel crystal planes in
terms of their normals, since as the planes are two
dimensional, their normals will be one dimensional
in nature.
27 February 2023 45
Reciprocal lattice

46. 1. Fix up some point in the direct lattice as a common origin.
2. From this common origin draw normals to each and every
set of parallel planes in the direct lattice.
3. Fix the length of each normal equal to the reciprocal of the
inter-planar spacing (1/dhkl
) of the set of parallel planes (h k l) it
represents.
4. Put a point at the end of each normal.
5. The collection of all these points in space is the reciprocal
lattice of the direct lattice.
27 February 2023 46
Geometrical construction of reciprocal lattice:

47. 27 February 2023 47

48. 27 February 2023 48
Reciprocal lattice

49. Session 5
27 February 2023 49

50. Importance of X-rays
27 February 2023 50

51. Production of X-Rays
27 February 2023 51
λ = 0.1 to 100 Å

52. Deriving Bragg’s Law, n = 2d sin
27 February 2023 52

53. 27 February 2023 53

54. Problems on Bragg’s law
1. A beam of X-rays of wavelength 0.071
nm is diffracted by (110) plane of rock
salt with lattice constant of 0.28 nm.
Find the glancing angle for the second-
order diffraction.
27 February 2023 54

55. 2. A beam of X-rays is incident on a NaCl
crystal with lattice plane spacing 0.282 nm.
Calculate the wavelength of X-rays if the
first-order Bragg reflection takes place at a
glancing angle of 8°35′. Also calculate the
maximum order of diffraction possible.
27 February 2023 55

56. 3. Monochromatic X-rays of λ = 1.5 Å are
incident on a crystal face having an inter-
planar spacing of 1.6 Å. Find the highest
order for which Bragg’s reflection
maximum can be seen.
27 February 2023 56

57. 4. For BCC iron, compute (a) the inter-
planar spacing, and (b) the diffraction angle
for the (220) set of planes. The lattice
parameter for Fe is 0.2866 nm. Also,
assume that monochromatic radiation
having a wavelength of 0.1790 nm is used,
and the order of reflection is 1.
27 February 2023 57

58. 5. The metal niobium has a BCC crystal
structure. If the angle of diffraction for
the (211) set of planes occurs at 75.990
(first order reflection) when
monochromatic X-radiation having a
wavelength 0.1659 nm is used.
Compute (a) the inter-planar spacing for
this set of planes and (b) the atomic
radius for the niobium atom.
27 February 2023 58

59. Session 6
27 February 2023 59

60. 27 February 2023
X-ray diffraction Methods
1. Laue Method 2. Rotating Crystal method
3. Powder Method
• Polychromatic Beam
• Diffraction angle is fixed
• Single Crystals
• Monochromatic Beam
• Variable diffraction angle
• Single Crystal
• Monochromatic Beam
• Variable diffraction angle
• Polycrystals (powder)
60

61. 2
tan(180 2 )
r
D

 
(b) Back-reflection method
27 February 2023
r1
2
White
X-rays
Collimator Single crystal
B
F
S
D
(a) Transmission method
r2
(180 -2 )
White
X-rays
Collimator
Single crystal
B
F
S
D
1
tan 2
r
D
 
1. Laue Method
61

62. Transmission
method
Back-reflection
method
27 February 2023 62

63. Experimental setup of
Rotation Crystal method
Cylindrical film
Axis of Crystal
Single crystal
2. Rotating Crystal Method
27 February 2023 63

64. 27 February 2023
3. Powder XRD Method
64

65. Determination of Lattice constant ‘a’
Applications of XRD in Crystallography
27 February 2023 65

66. X-Ray Diffraction technique is used to
 Distinguish between crystalline &
amorphous materials.
 Determine the structure of crystalline
materials.
 Determine the lattice parameters.
 Determine the electron distribution
within the atoms, & throughout the
unit cell.
27 February 2023 66

67.  Determine the symmetry and
orientation of single crystals.
 Determine the texture of polygrained
materials.
 To measure the strain and small
grain size…..etc.
 To identify defects and small cracks in
materials and to determine their sizes.
27 February 2023 67

68. Advantages
Advantages & Disadvantages of
X-Ray Diffraction
27 February 2023
 XRD is a non-destructive technique.
 X-Rays are the least expensive, the most
convenient & the most widely used method to
determine crystal structures.
 X-Rays are not absorbed very much by air, so
the sample need not be in an evacuated
chamber.
Disadvantages
 X-Rays do not interact very strongly with lighter
elements.
68

69. 1. Chromium has BCC structure. Its atomic
radius is 0.1249 nm . Calculate the free
volume / unit cell.
2. Lithium crystallizes in BCC structure.
Calculate the lattice constant, given that
the atomic weight and density for lithium
are 6.94 and 530 kg/m3 respectively.
Problems
27 February 2023 69

70. 3. Iron crystallizes in BCC structure.
Calculate the lattice constant, given that
the atomic weight and density of iron
are 55.85 and 7860 kg/m3 respectively.
4. If the edge of the unit cell of a cube in
the diamond structure is 0.356 nm,
calculate the number of atoms/m3.
27 February 2023 70

71. 5. A metal in BCC structure has a lattice
constant 3.5 Å. Calculate the number of
atoms per sq. mm area in the (200)
plane.
6. Germanium crystallizes in diamond
(from) structures with 8 atoms per unit
cell. If the lattice constant is 5.62 Å,
calculate its density.
27 February 2023 71

72. 7. A beam of X-rays of wavelength 0.071
nm is diffracted by (100) plane of rock salt
with lattice constant of 0.28 nm. Find the
glancing angle for the second order
diffraction.
27 February 2023 72

73. 8. A beam of X-rays is incident on a NaCl
crystal with lattice plane spacing 0.282
nm. Calculate the wavelength of X-rays if
the first-order Bragg reflection takes
place at a glancing angle of 8o 35’. Also
calculate the maximum order of
diffraction possible.
9. The fraction of vacant sites in a metal
is 1 X 10-10 at 500 oC. What will be the
fraction of vacancy sites at 1000 oC?
27 February 2023 73

74. 10. Calculate the ratios of d100 : d110 : d111
for a simple cubic structure
11. The Bragg’s angle in the first order
for (220) reflection from nickel (FCC) is
38.2o. When X-rays of wavelength 1.54
Å are employed in a diffraction
experiment. Determine the lattice
parameter of nickel.
27 February 2023 74

75. 12. Monochromatic X-rays of  = 1.5 Å
are incident on a crystal face having an
inter-planar spacing of 1.6 Å. Find the
highest order for which Bragg’s
reflection maximum can be seen.
13. Copper has FCC structure with
lattice constant 0.36 nm. Calculate the
inter-planar spacing for (111) and (321)
planes.
27 February 2023 75

76. 14. The distance between (100) planes
in a BCC structure is 0.203 nm. What is
the size of the unit cell? What is the
radius of the atom?
15. Monochromatic X-rays of  = 1.5 Å
are incident on a crystal face having an
inter-planar spacing of 1.6 Å. Find the
highest order for which Bragg’s reflection
maximum can be seen.
27 February 2023 76

77. 16. The first order diffraction occurs when
a X-ray beam of wavelength 0.675 Å
incident at a glancing angle 50 25’ on a
crystal. What is the glancing angle for
third-order diffraction to occur?
17. The Bragg’s angle in the first order for
(220) reflection from nickel (FCC) is 38.20.
When X-rays of wavelength 1.54 Å are
employed in a diffraction experiment.
Determine the lattice parameter of nickel.
27 February 2023 77