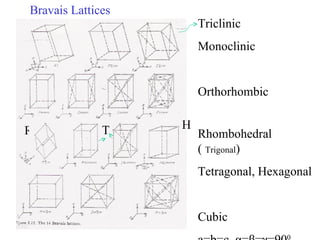
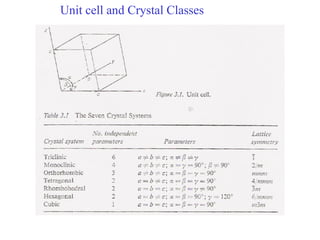
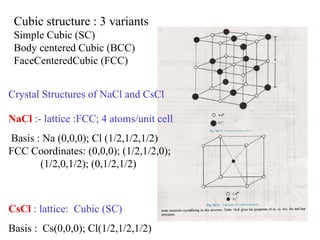
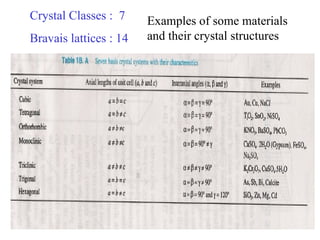
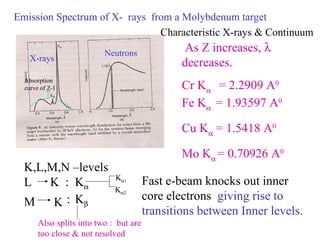
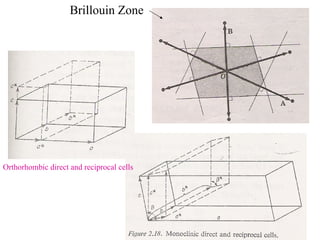
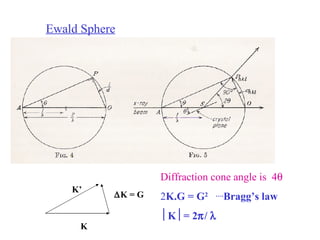
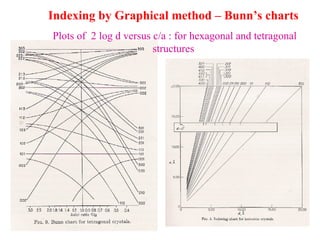
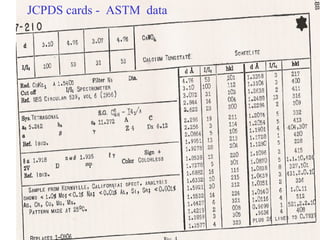
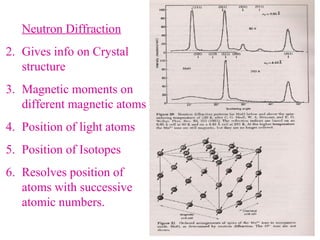
The document discusses crystal structure determination using X-ray diffraction. It describes how X-rays are used to probe interatomic distances in solids and explains key concepts like Bragg's law, reciprocal lattices, and Miller indices that are used to index diffraction patterns and determine unit cell parameters and crystal structures. Examples of common crystal structures like NaCl, CsCl are given along with methods to analyze diffraction data.

1. Crystal Structure using X – ray Diffraction X-rays of the order of  1Ǻ wavelength are used to probe the structural information in solid Interatomic distances  a few Ǻ ( m,n,p) are coordinates of a point [100] represents the direction of the vector from origin to (1,0,0) Miller Indices are h,k, l if 1/h, 1/k, 1/ l are the intercepts along X,Y,Z axes Cubic : {100} = (100), (010),(001), (100), (010),(001) Tetragonal :{ 100} = (100), (010), (100), (010) (100) (001) 0 (200) X Y Z (1,0,0) Cubic unit cell

2. Bravais Lattices Triclinic Monoclinic Orthorhombic Rhombohedral ( Trigonal ) Tetragonal, Hexagonal Cubic a=b=c, α = β = γ =90 0 R H T

3. Unit cell and Crystal Classes

4. Crystal Structures of NaCl and CsCl NaCl :- lattice :FCC; 4 atoms/unit cell Basis : Na (0,0,0); Cl (1/2,1/2,1/2) FCC Coordinates: (0,0,0); (1/2,1/2,0); (1/2,0,1/2); (0,1/2,1/2) CsCl : lattice: Cubic (SC) Basis : Cs(0,0,0); Cl(1/2,1/2,1/2) SC coordinates : (0,0,0) Cubic structure : 3 variants Simple Cubic (SC) Body centered Cubic (BCC) FaceCenteredCubic (FCC)

5. Crystal Classes : 7 Bravais lattices : 14 Examples of some materials and their crystal structures

6. To produce X- rays of  1 Ǻ photons of energy :  12.4 keV need be generated because E = h  = h c /   (in m) = h c / E(Joules);  = 12398  0 / E(eV) 1  0 = 10 -8 cm= 10 -10 m = 10 -4  m (microns) Energy of n th level E n = h Z 2 R/ n 2 - in an element of At. No. Z Energy released h  ( m n ) = h Z 2 R ( ( 1/ n 2 ) – ( 1 / m 2 ) )    Z 2    1 / Z 2 Common targets used to produce X rays are Cr, Fe, Cu, and Mo Higher the Z value lower is the  of K  radiation. Production of X - rays

7. Emission Spectrum of X- rays from a Molybdenum target As Z increases,  decreases. Cr K  = 2.2909 A 0 Fe K  = 1.93597 A 0 Cu K  = 1.5418 A 0 Mo K  = 0.70926 A 0 K,L,M,N –levels L K : K  Fast e-beam knocks out inner core electrons giving rise to transitions between Inner levels. K  1 K  2 M K : K  Neutrons X-rays Also splits into two : but are too close & not resolved Characteristic X-rays & Continuum Absorption curve of Z-1

8. Monochromatic X- rays using Filters Energy levels in an atom K  L  L K  K  1 , K  2 K  L  M K  K  1 , K  2 K  L N M K If X-ray target element is of Atomic No. Z the absorption edge of the (Z-1) element overlaps the K  peak of the element Z. Hence Cu target + Ni filter gives monochromatic CuK  radiation Target Filter Cr Fe Cu Mo V Mn Ni Nb

9. Bragg’s Law Incident ray 2  2 d h k l sin  h k l = n  d h k l --- normal distance between a set of parallel planes with (hkl) as Miller Indices.  h k l --- Bragg angle for (hkl) planes n --- order of diffraction  --- Wavelength of incident radition (X-rays, here). 1.Bragg’s law selects the Bragg angle for a given set of d hkl planes 2. Scattering amplitude and hence intensity of Bragg peak is decided by the structure factor d hkl

10. Debye – Scherrer method Diffraction cones cut the Sphere of reflections (Ewald sphere) in circles. These circles cut the film in arcs.So, a pair of arcs represents one diffraction cone corresponding to one set of d hkl planes .

11. XRD pattern- Debye-Scherrer film Various diffraction cones cut the film in sets of arcs Each pair of arcs represents diffraction from one set of (hkl) planes Number of arcs between the 2 holes define the number of observed Bragg diffraction lines

12. Reciprocal Lattice (RL) picture 2 d h k l sin  h k l = n  sin  = (1 / d ) / ( 2/  ) for n = 1 For a given  , sin  goes as (1 / d ) Direct lattice vector r = m a +n b+ p c Reciprocal lattice vector G = h a * + k b * + l c * d hkl = 2  /  G hkl  A point in RL represents a set of planes in the direct lattice . Vector length  G hkl  = 2  / d hkl

13. Reciprocal Vectors

14. Orthorhombic direct and reciprocal cells Brillouin Zone

15. Ewald Sphere K K’  K = G Diffraction cone angle is 4  2 K.G = G 2 …. Bragg’s law  K  = 2  / 

16. Reflections for two different wavelengths in RL space Spheres of reflection : diameter = 2/  2 d h k l sin  h k l = n  1. (hkl) plane with smallest indices has largest d h k l & smallest  2. Maximum  or least possible d h k l observable is limited by  /2 which is Mo K  : 0.354 A 0 Cu K  : 0.771 A 0 Fe K  : 0.9679 A 0

17. Arc measurements Identify Forward ( low angle)and Backward ( higher angle) Reflections 2. Doublets at higher angles are due to K  1 and K  2 having different wavelengths

18. Relation between d - spacings and lattice parameters

19. Analytical methods Camera diameter is chosen to be : 2r = 180/  = 57.3 mm. B A Measure S, Calculate 2  , then Sin  for each arc. Calculate d-spacings . Index the planes – i.e. identify hkl for each d-spacing Cubic : (1/d) 2 = ( h 2 + k 2 + l 2 ) / a 2 gives value of ‘a’ B – A = 180 0

20. Structure Factor F hkl =  k f s exp(-2  i(hx+ky+lz)) ; here f s is the Form factor α electron density exp(-n  i) =1 for even n ; = -1 for odd n Finite Intensity for Bragg diffraction requires F hkl ≠ 0 1. BCC : F hkl summed over 2 terms gives Condition (h+k+l)= even no. 2. FCC : F hkl summed over 4 terms gives Condition (h+k),(k+l), (l+k) = all even numbers, i.e. h,k,l are all even or all odd With ( h 2 + k 2 + l 2 ) =N, the above conditions give Simple cube : N = 1,2,3,4, ….. except 7,15,23, … BCC : N = 2,4,6,8,10,….. FCC : N = 3,4,8,11,12,16,19,20,……

21. Indexing by Graphical method – Bunn’s charts Plots of 2 log d versus c/a : for hexagonal and tetragonal structures

22. JCPDS cards - ASTM data

23. Laue method for single crystals – uses white X-radiation

24. Neutron Diffraction Gives info on Crystal structure Magnetic moments on different magnetic atoms Position of light atoms Position of Isotopes Resolves position of atoms with successive atomic numbers.