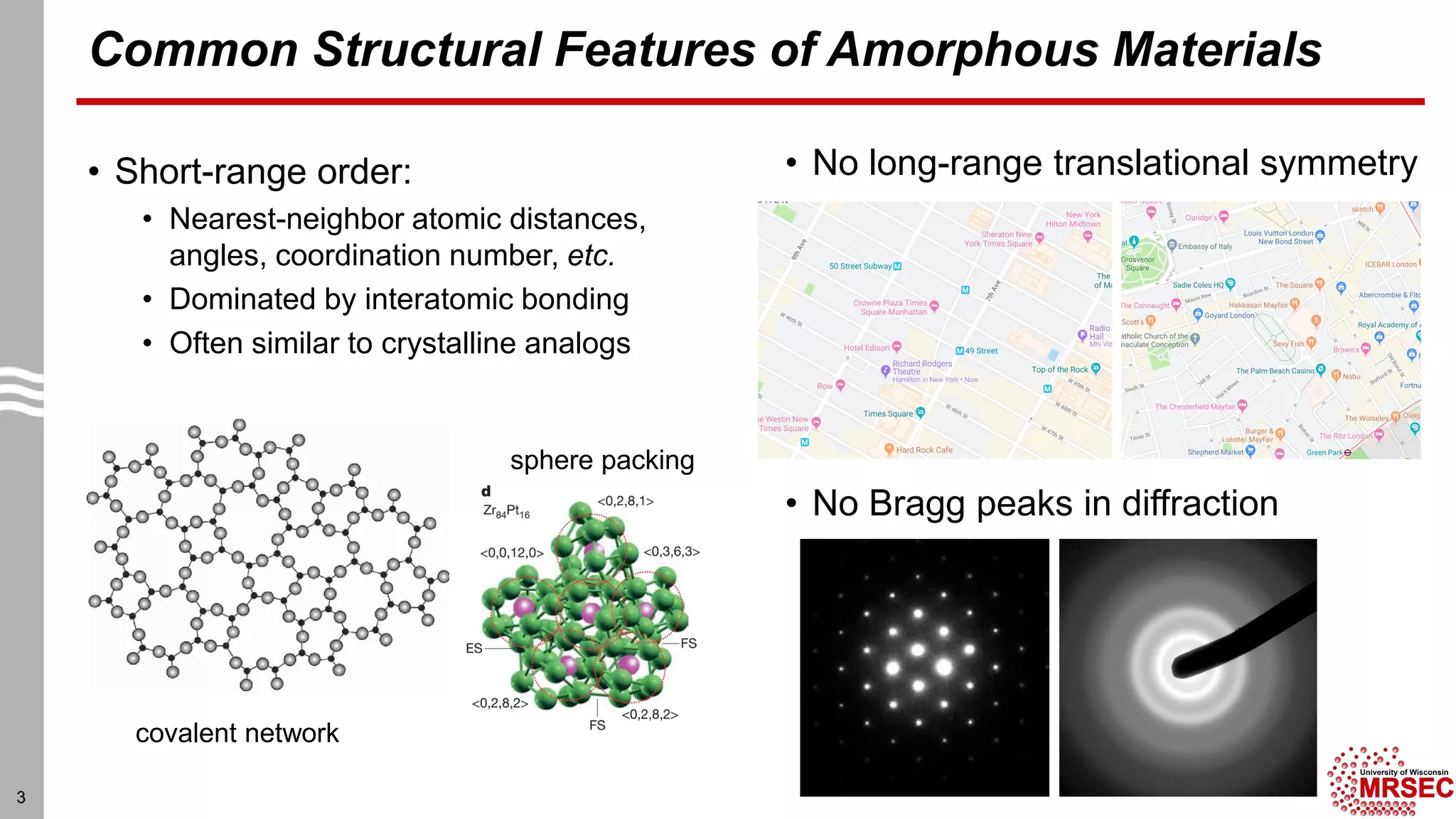
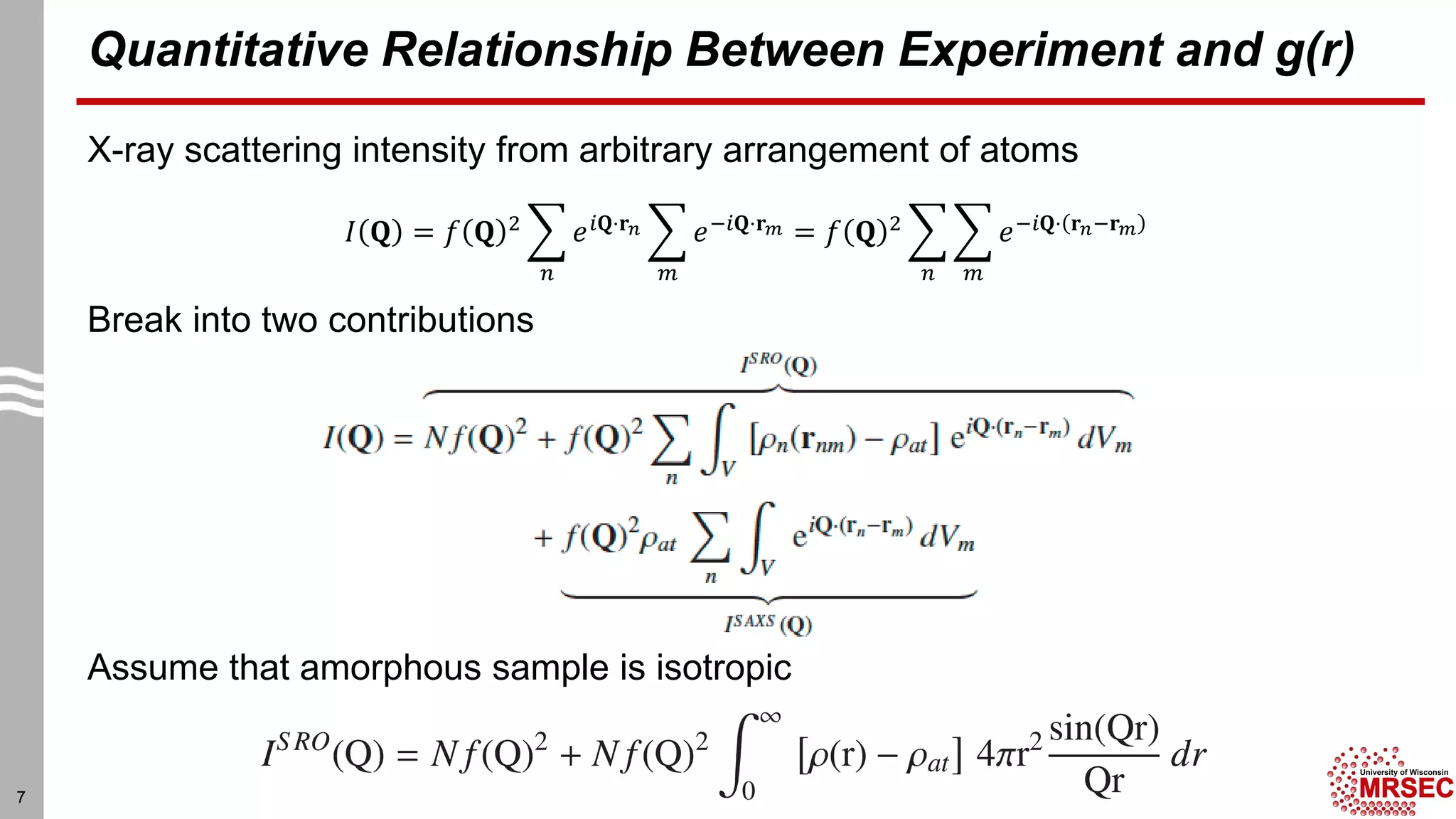
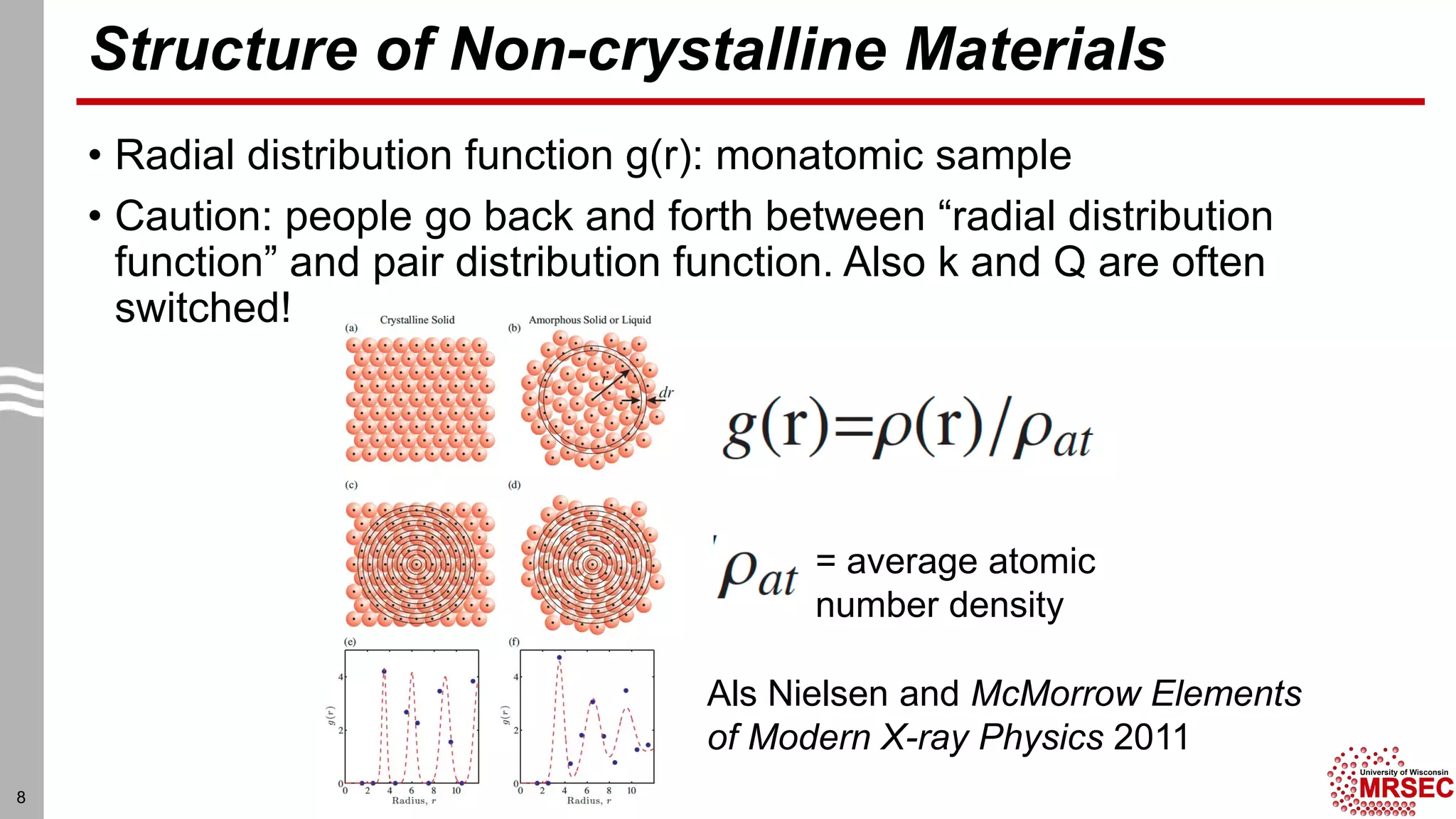
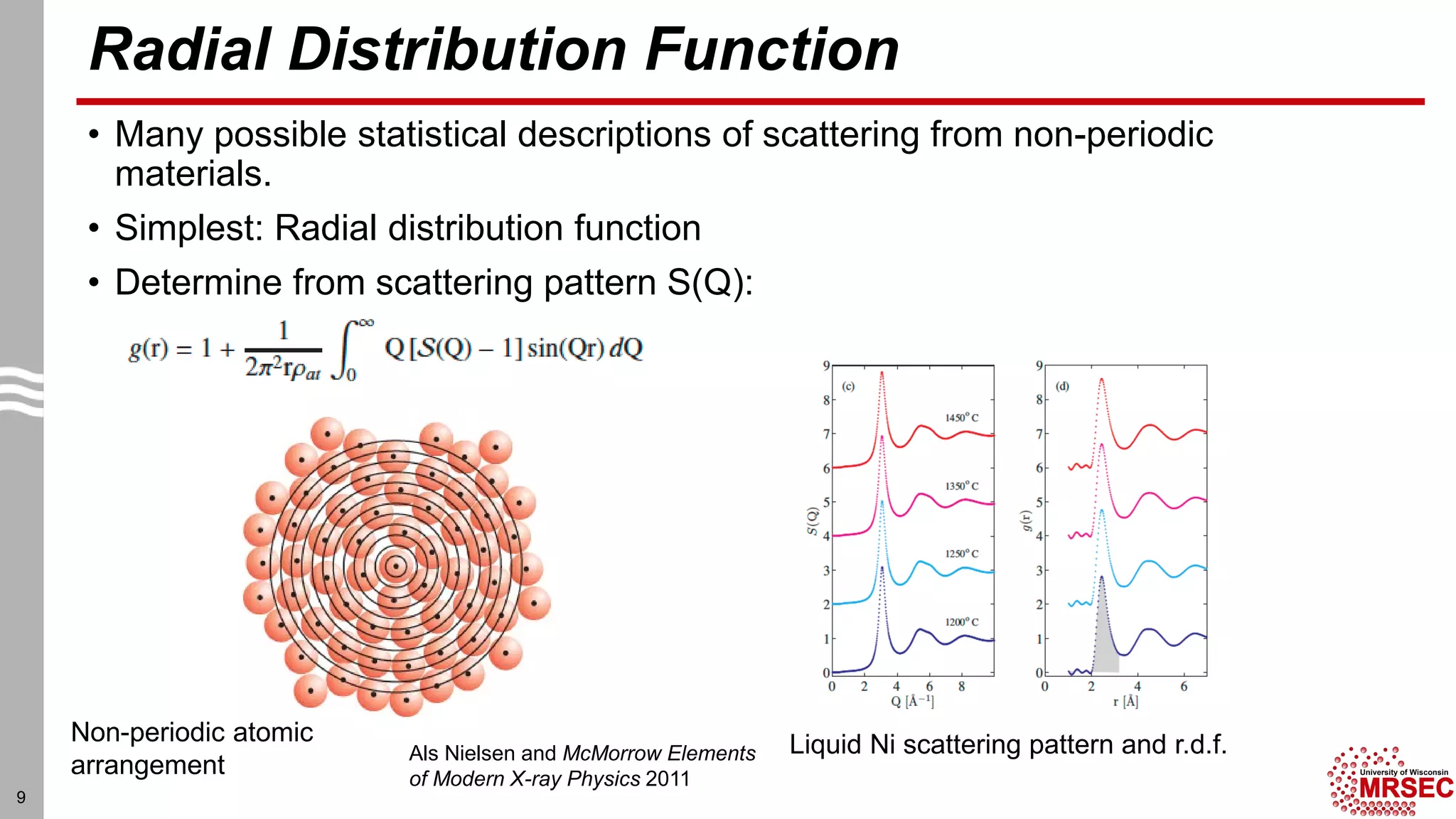
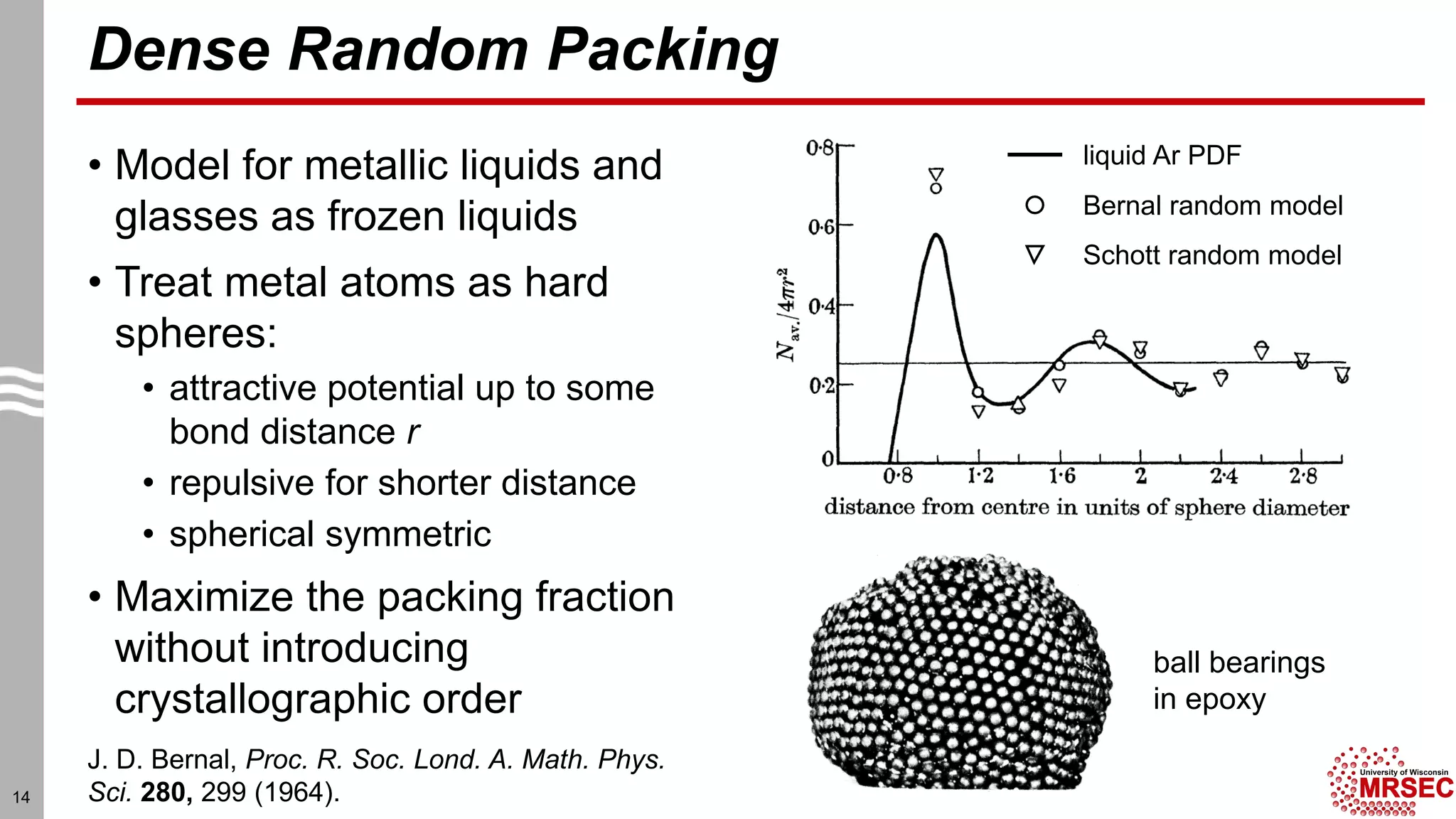
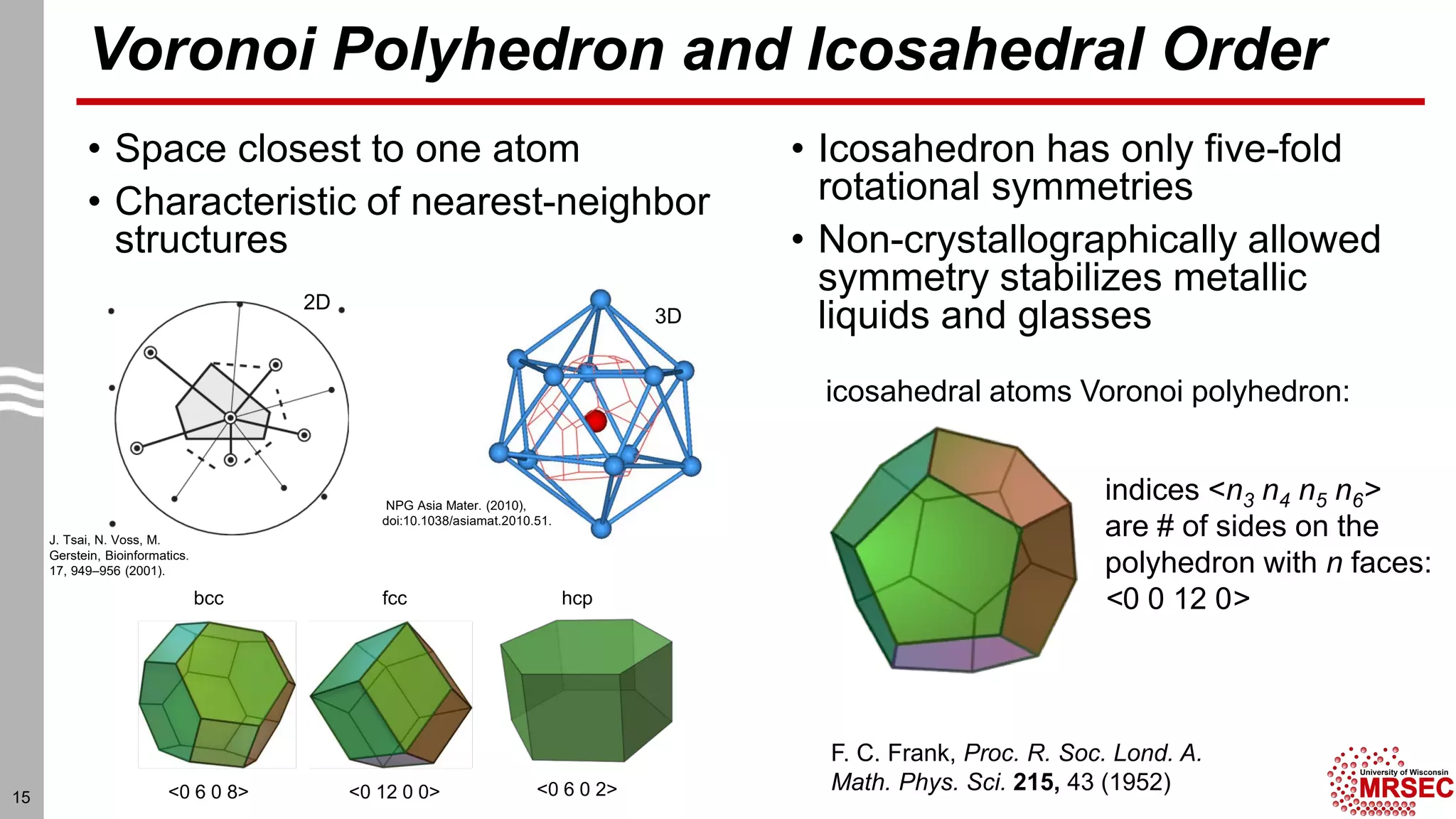
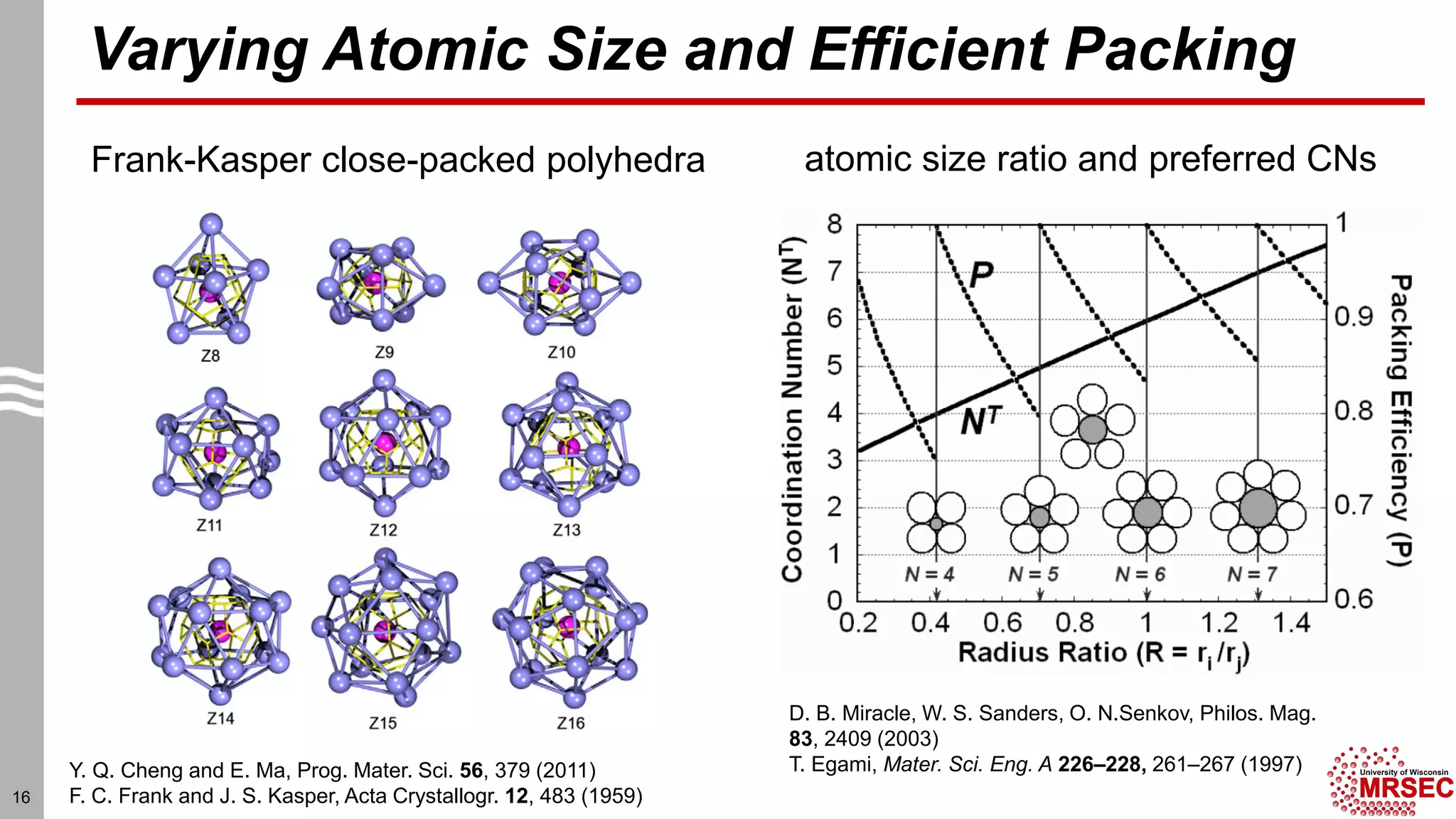
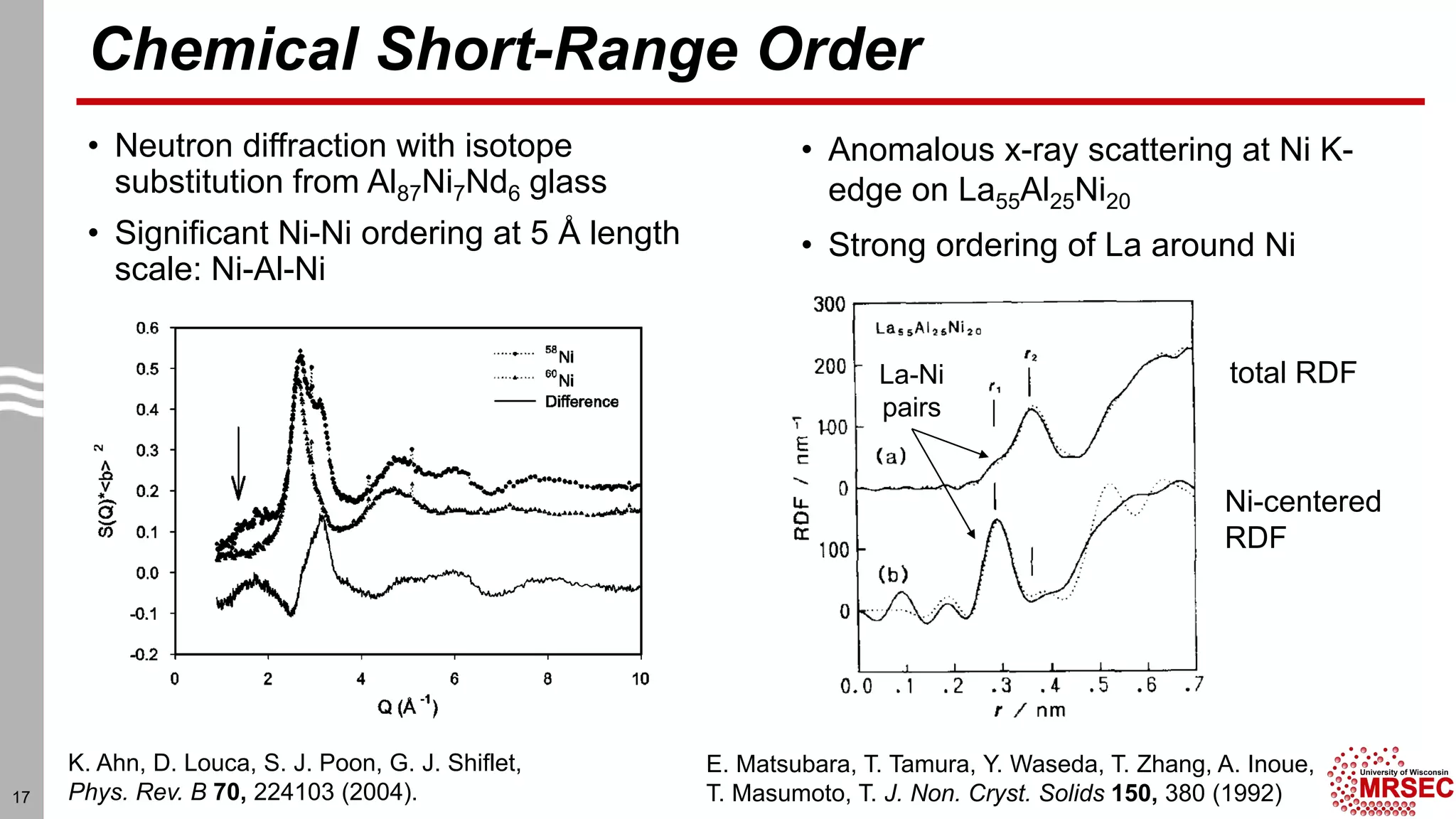
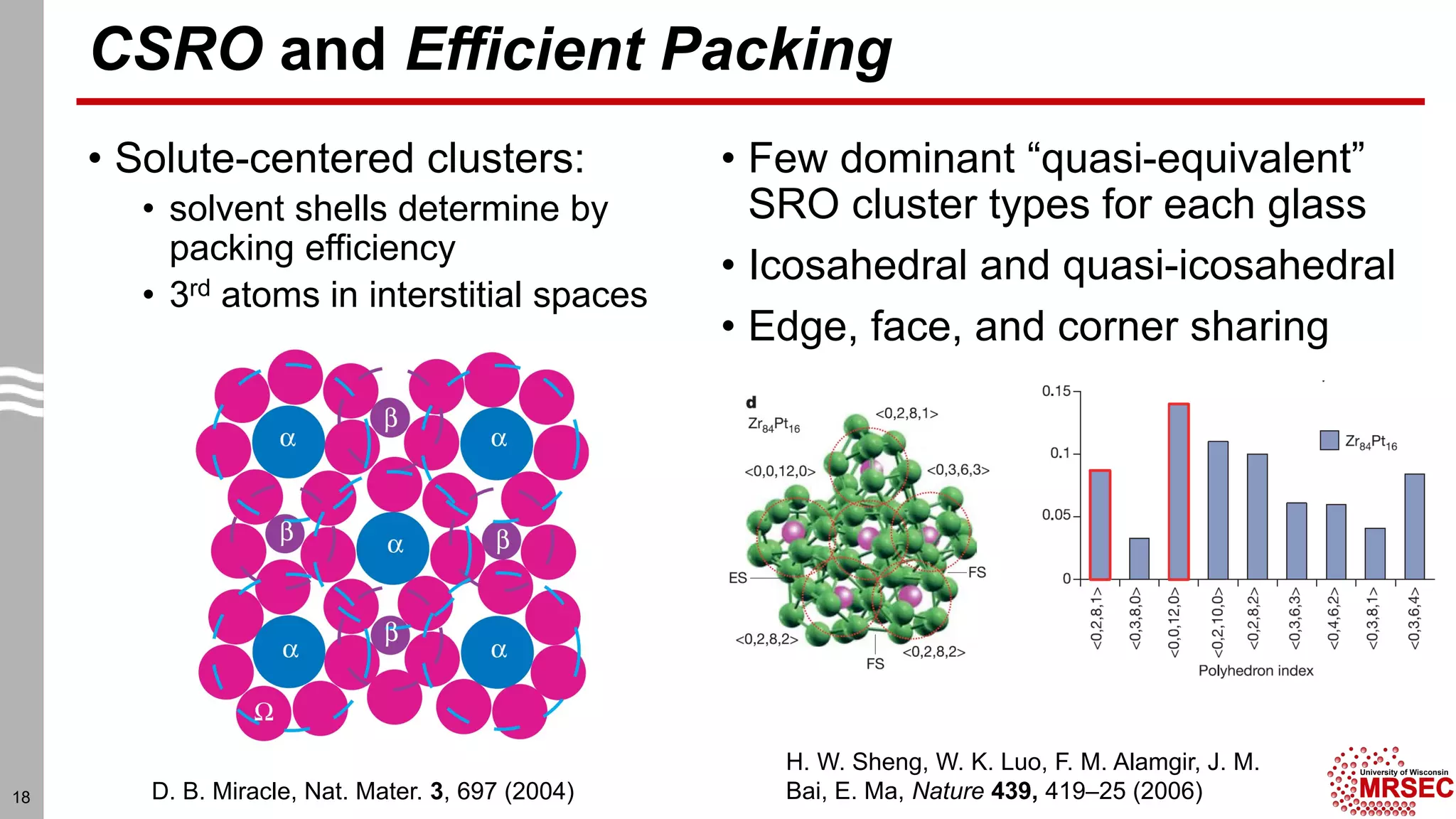
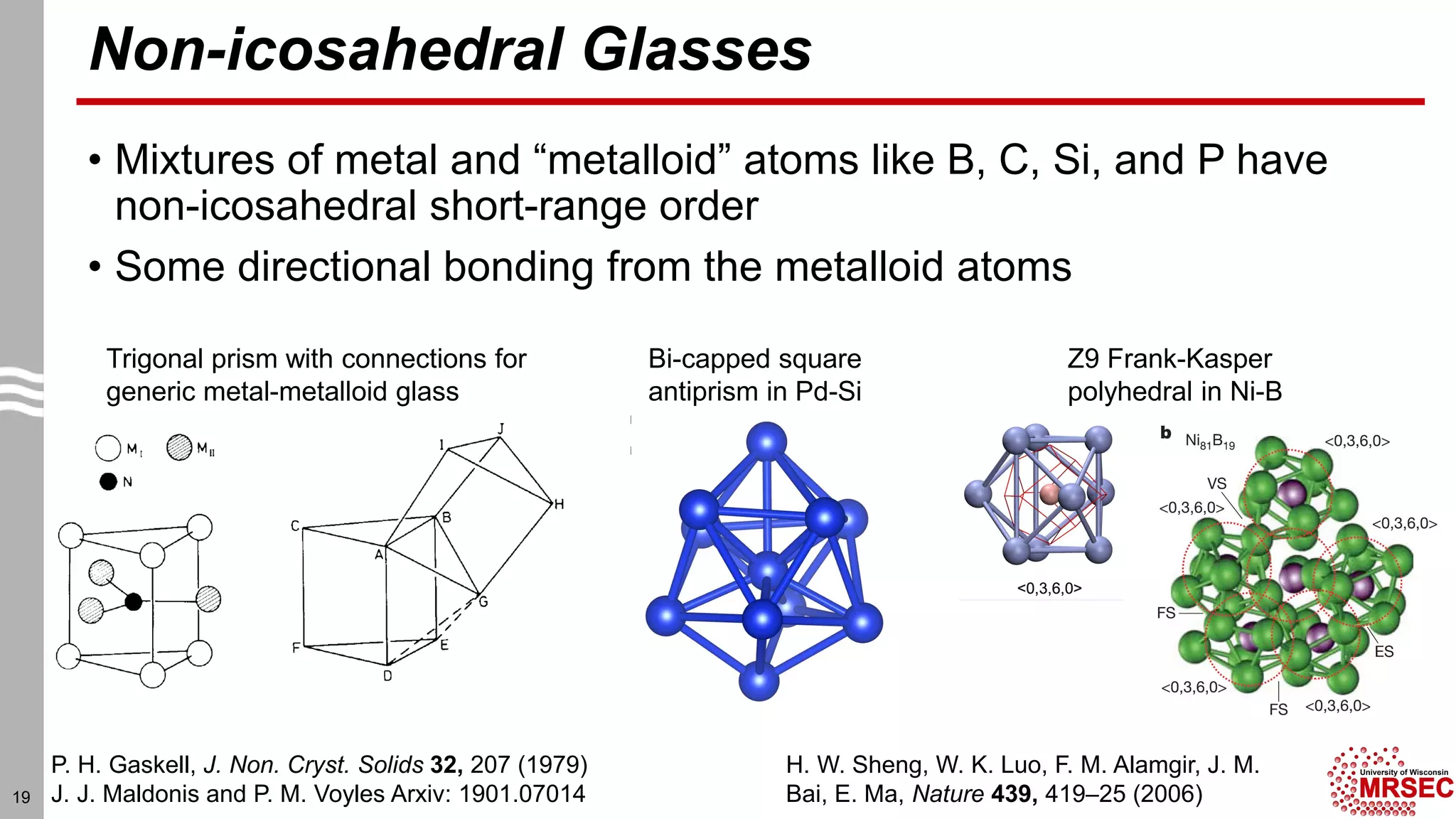
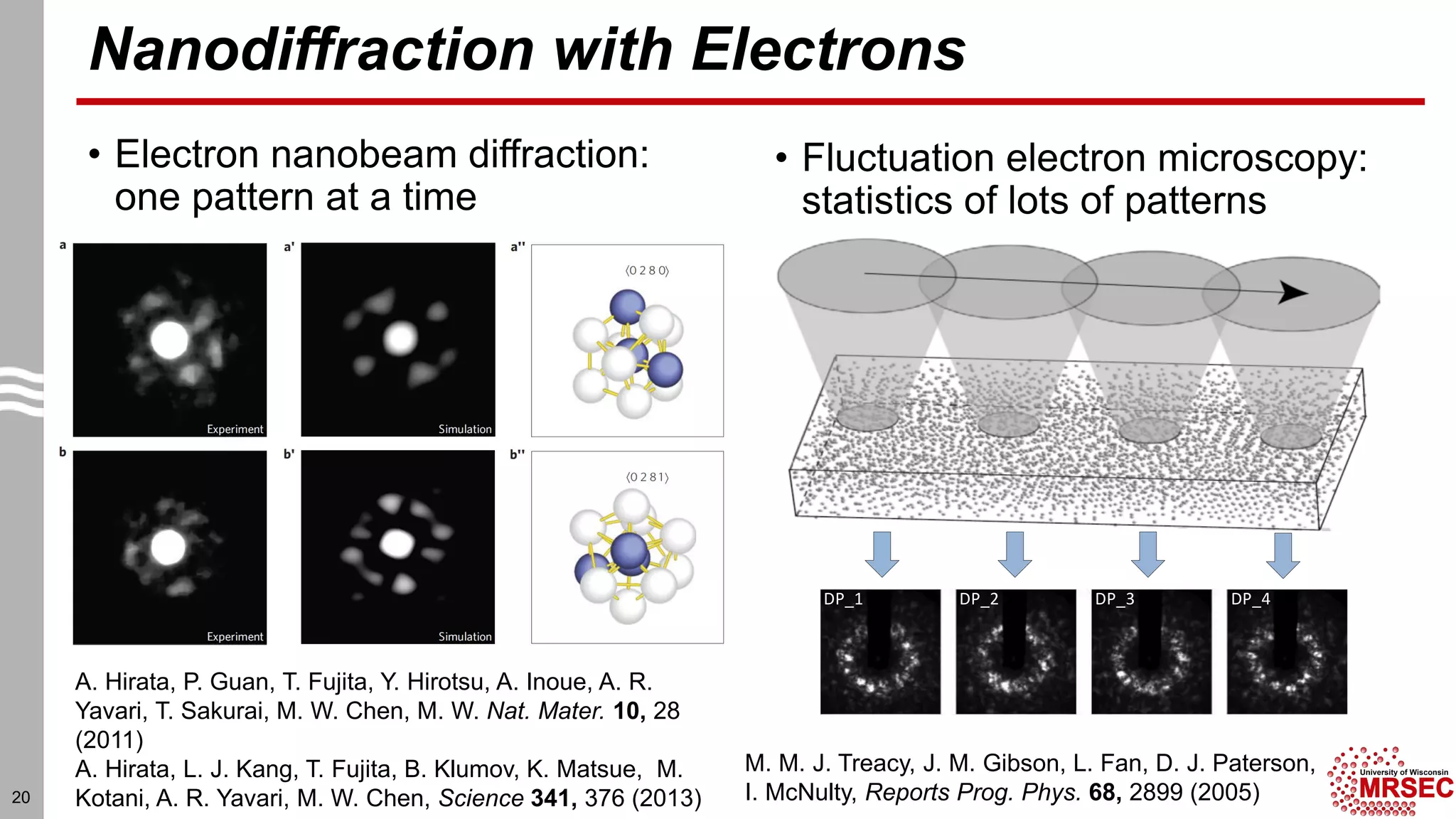
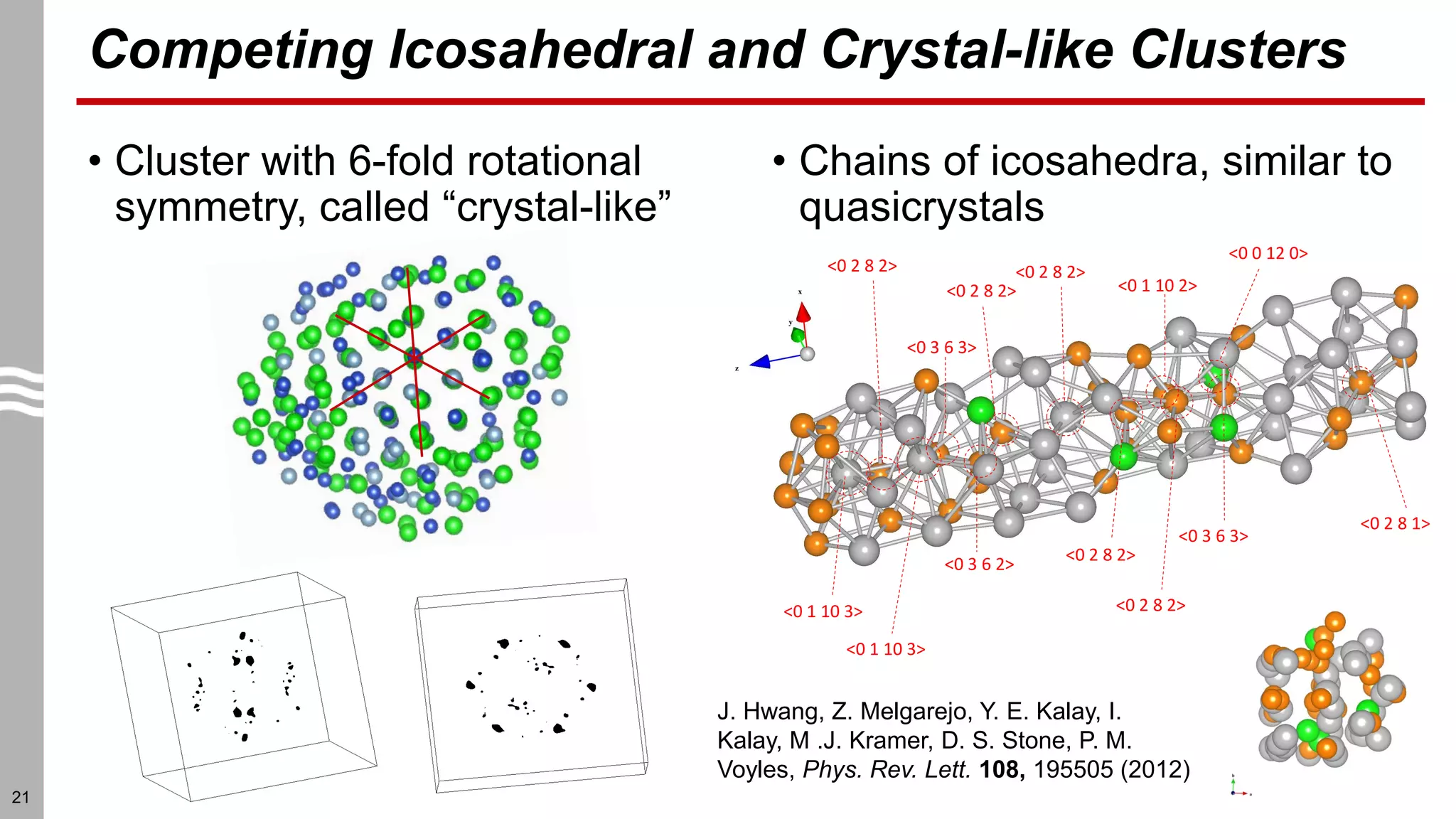
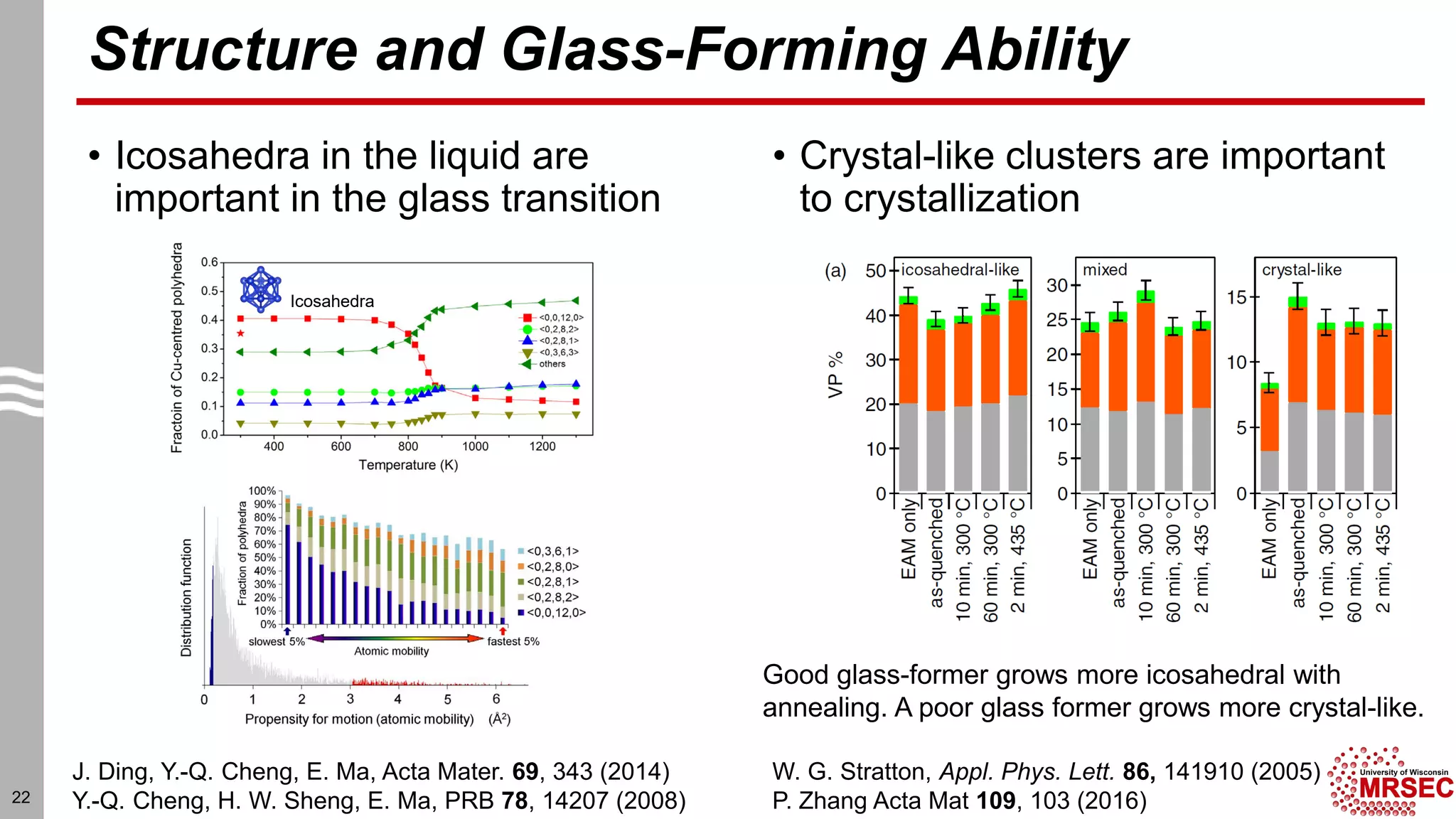
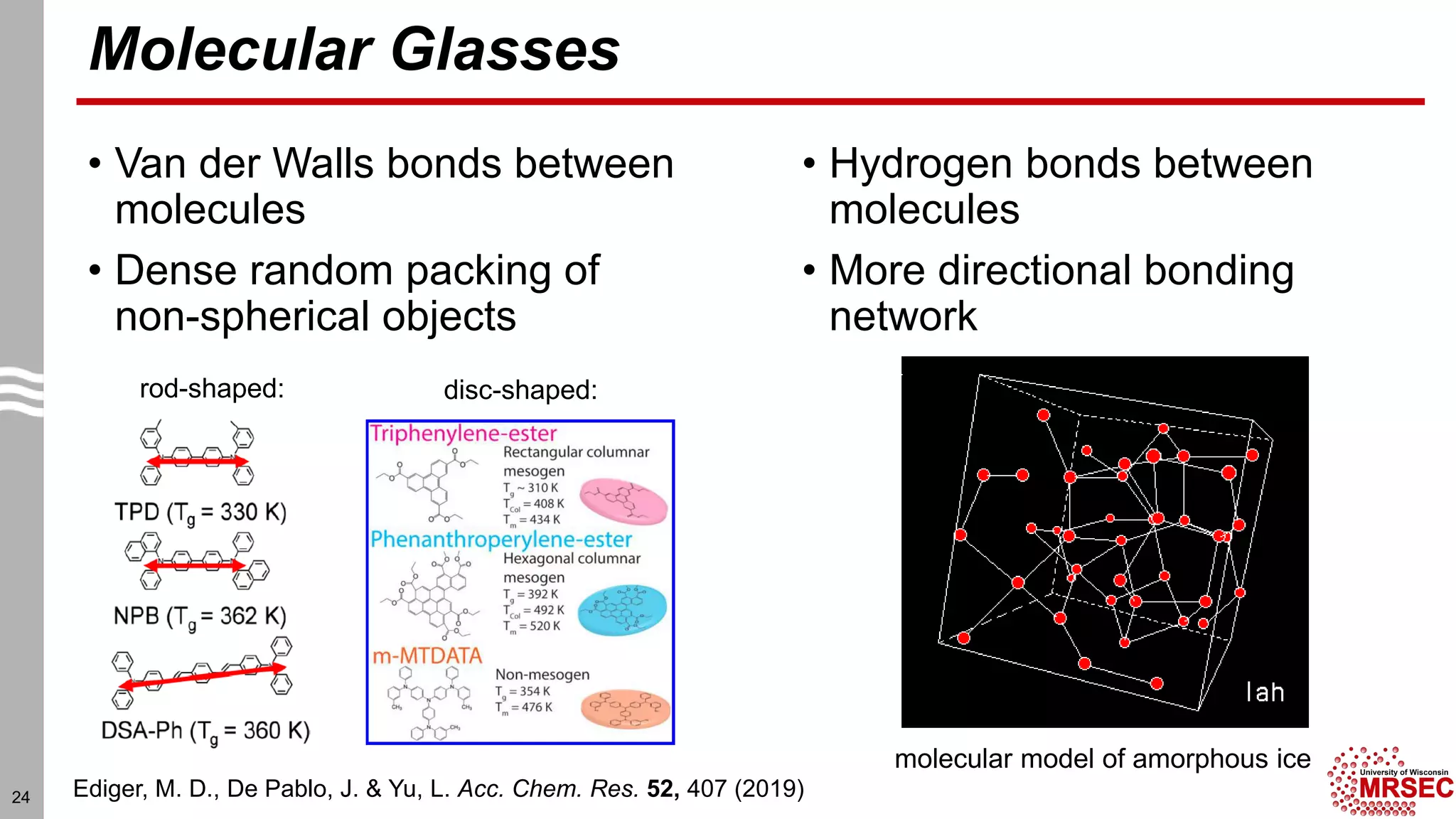
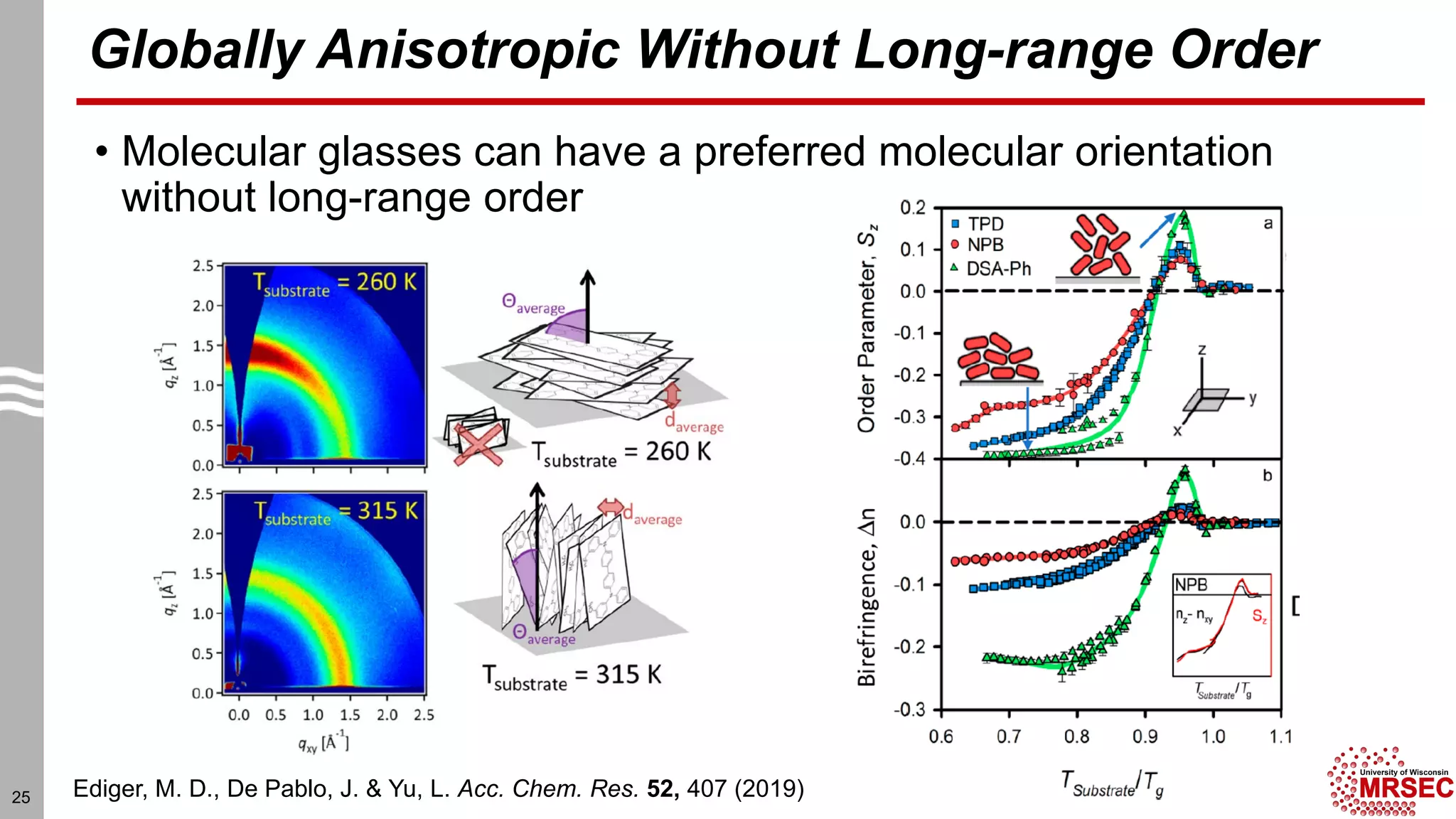
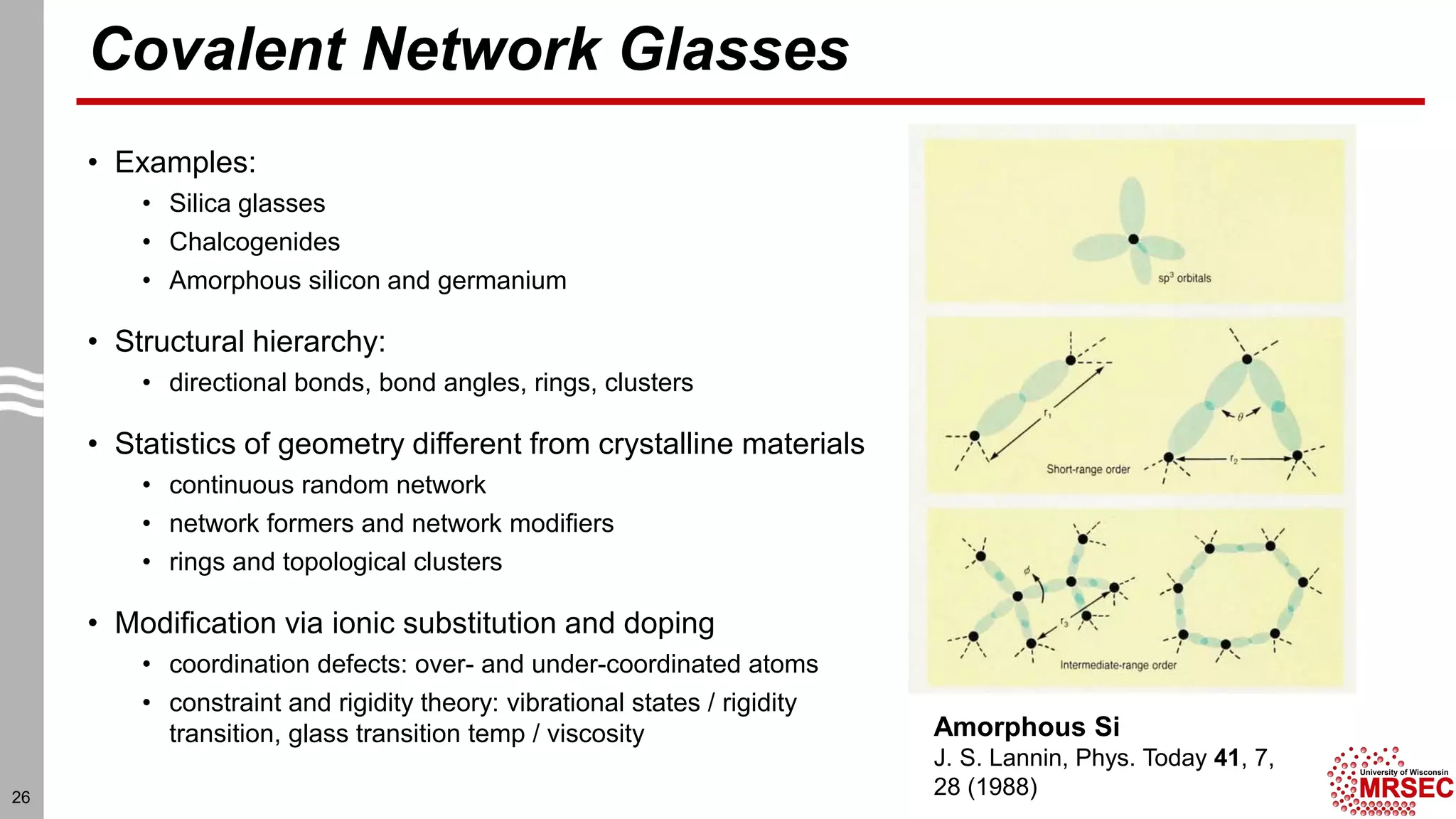
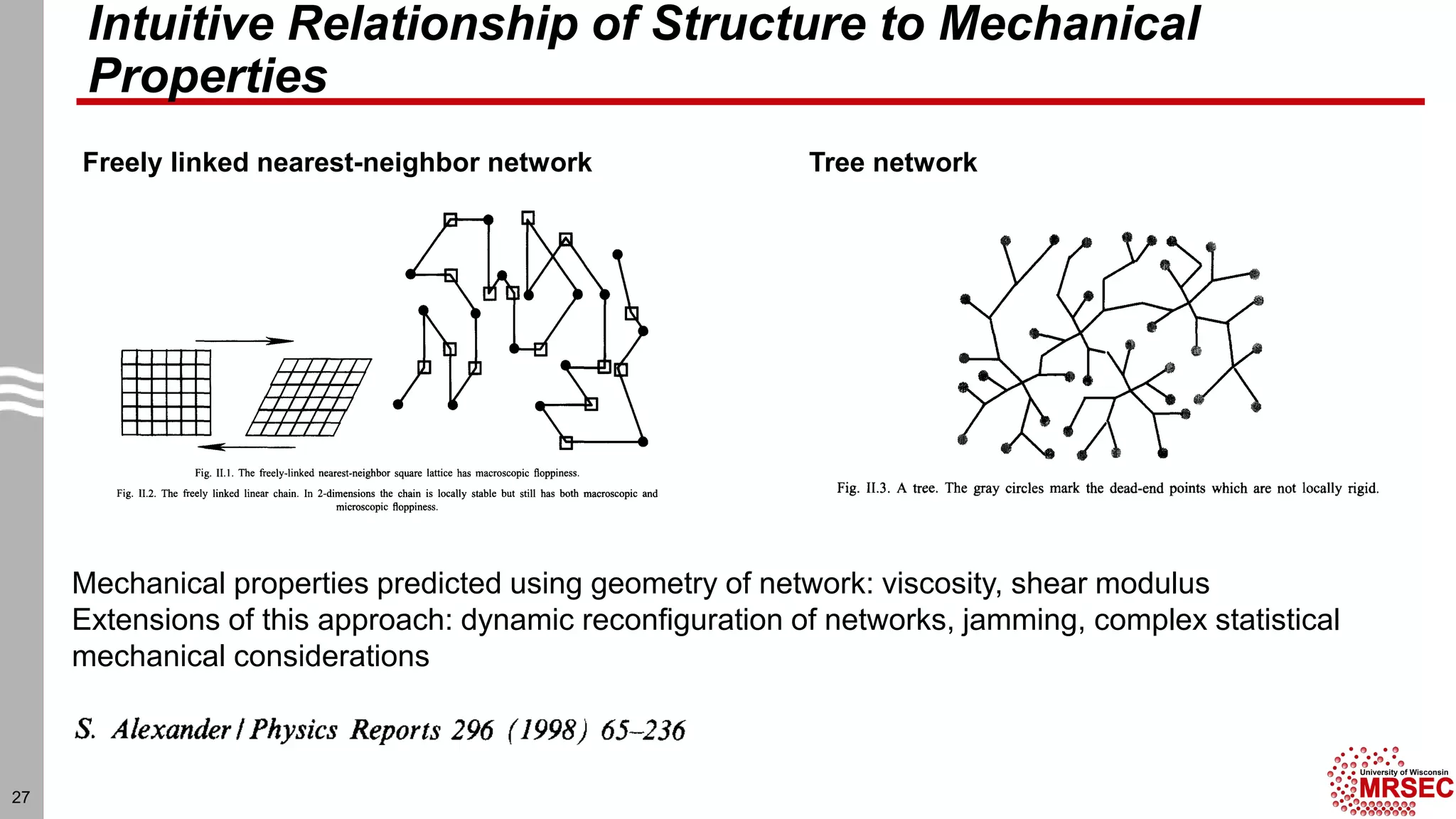
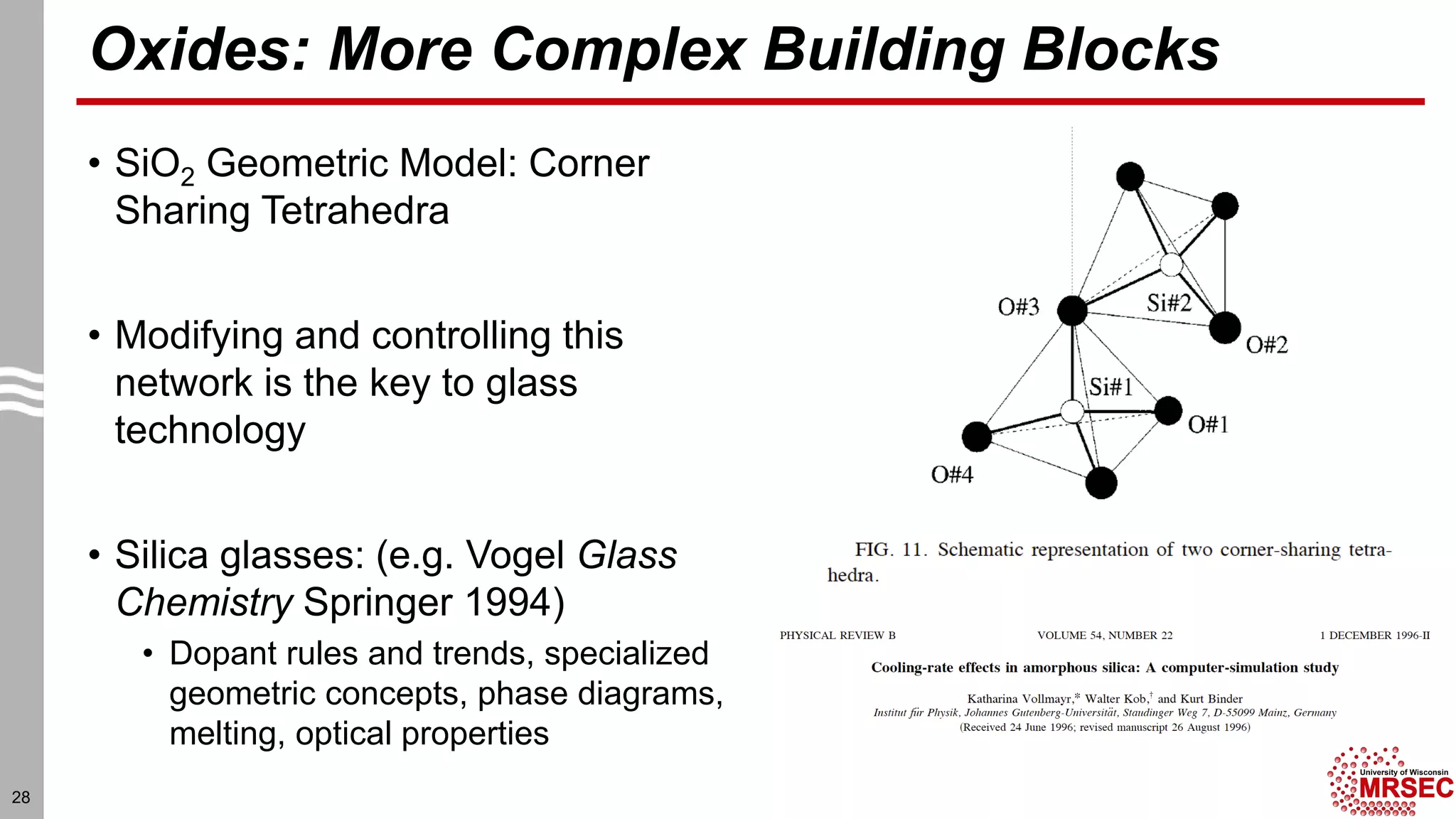
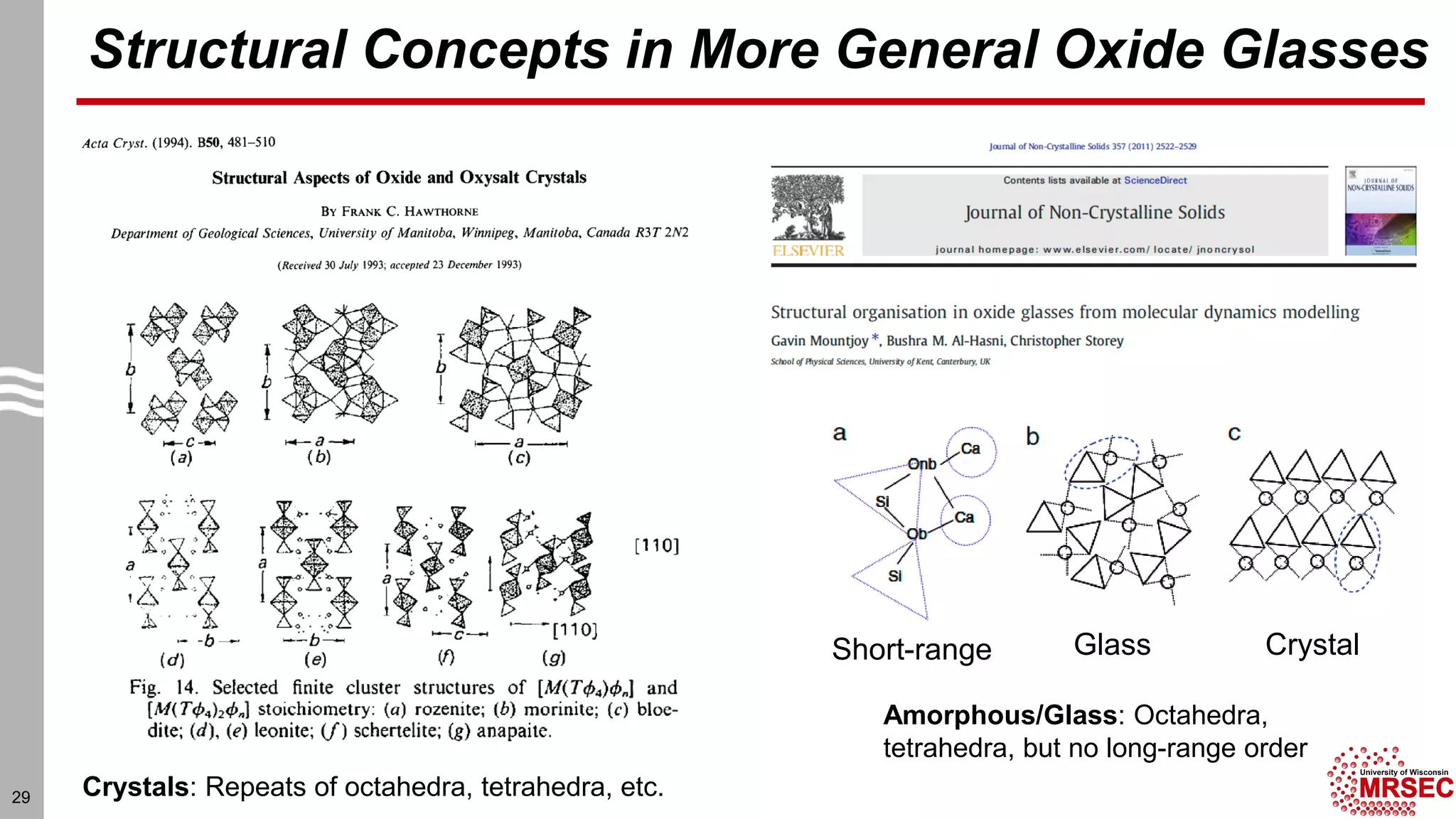
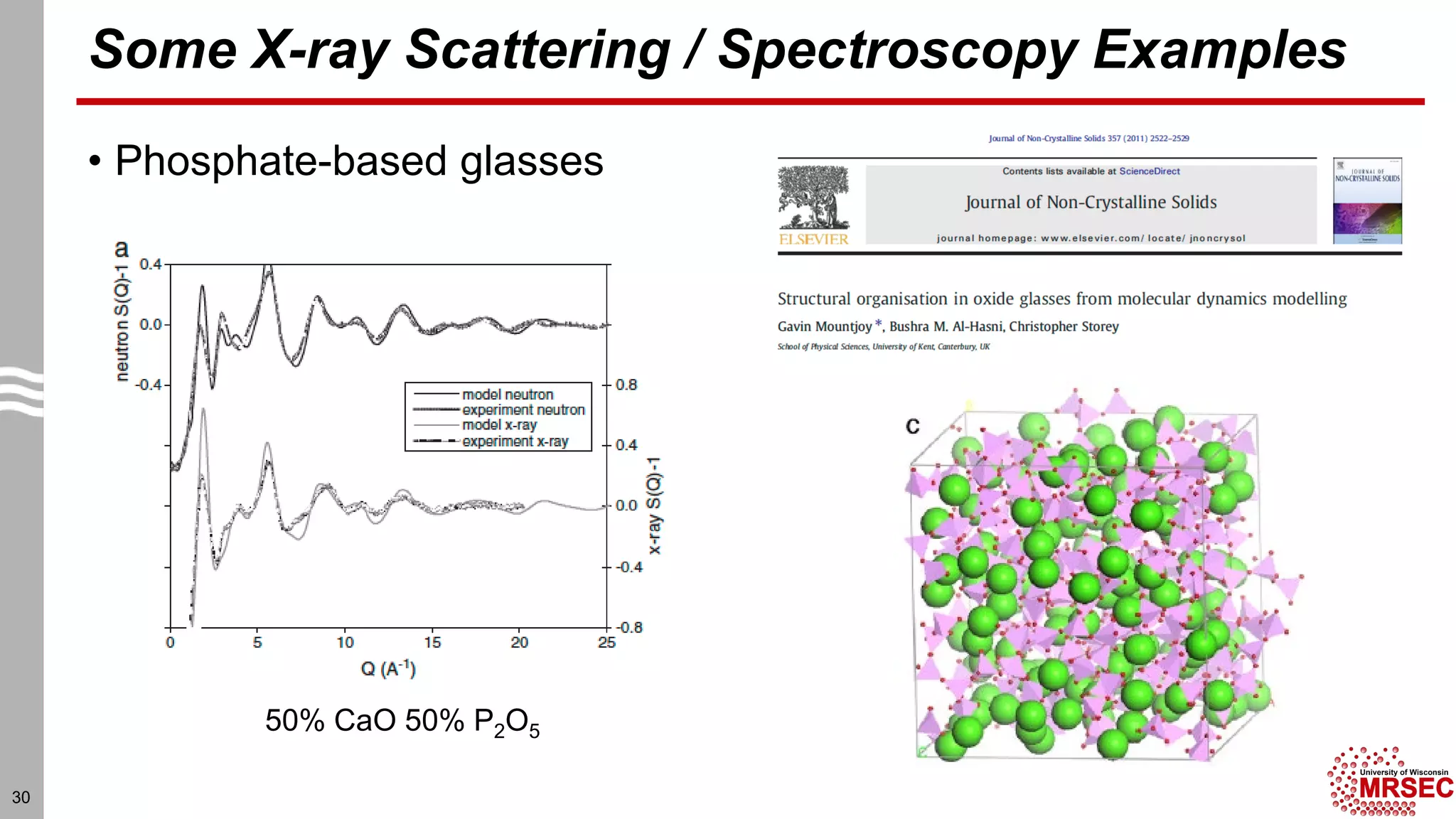
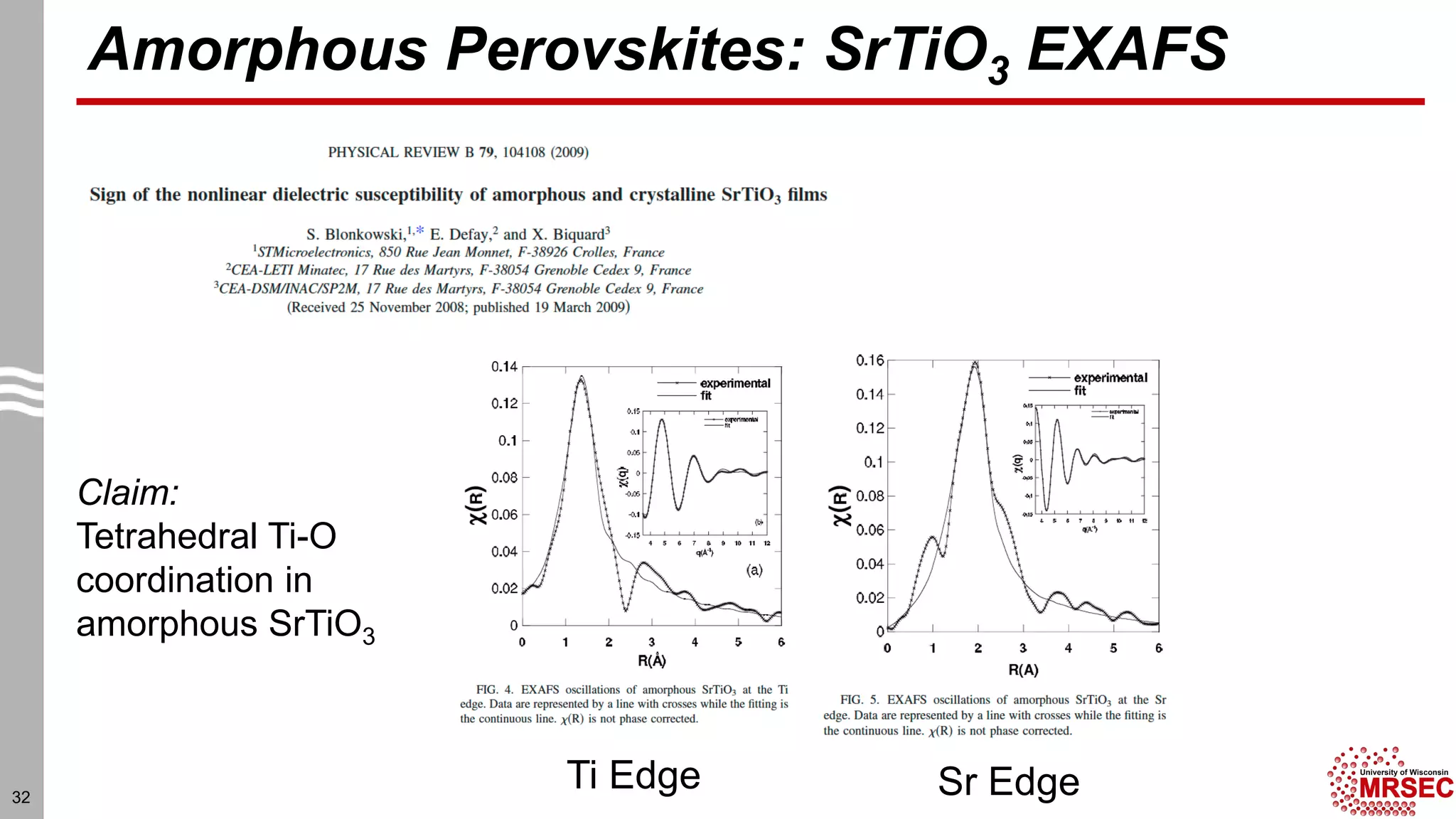
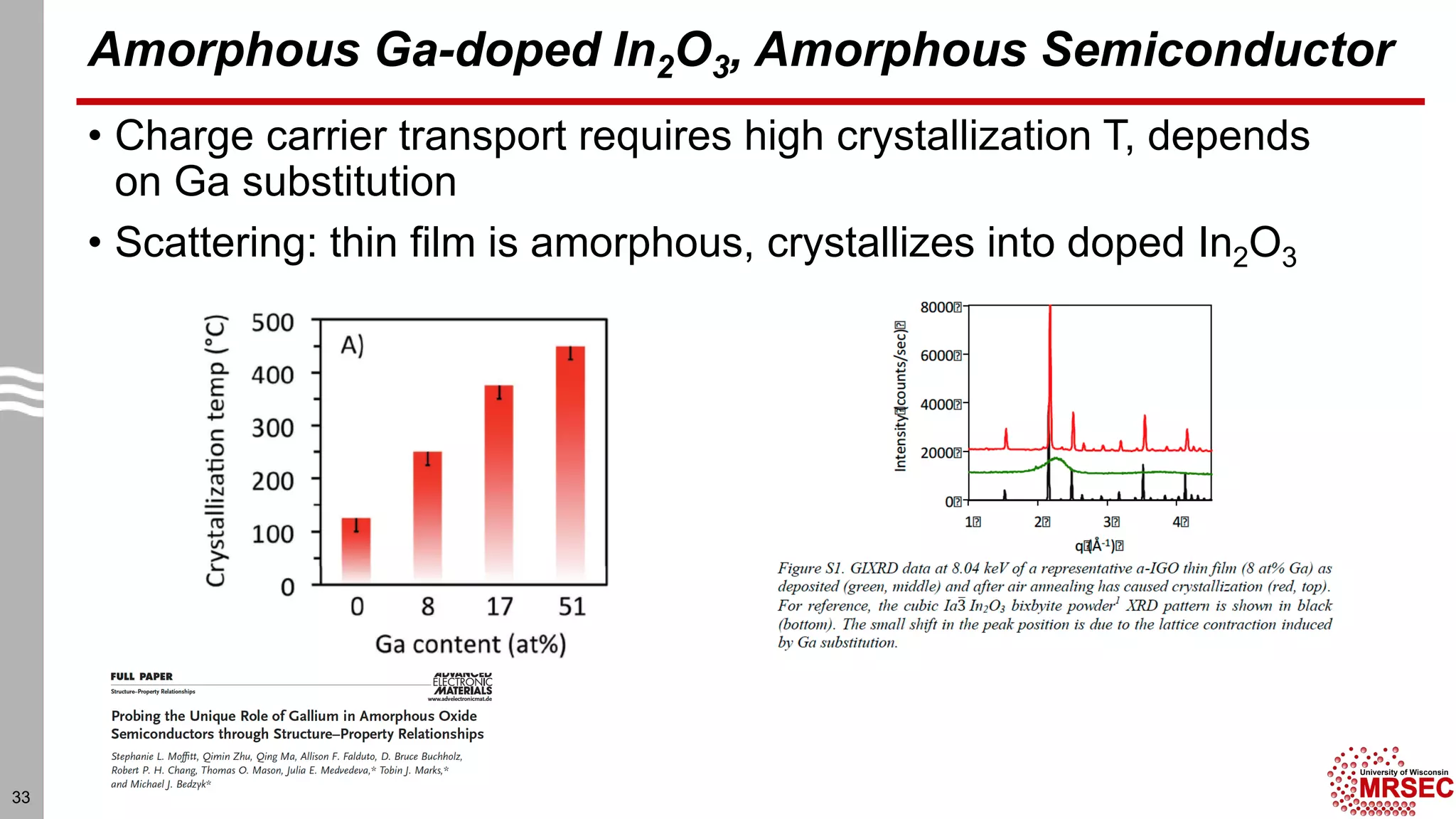
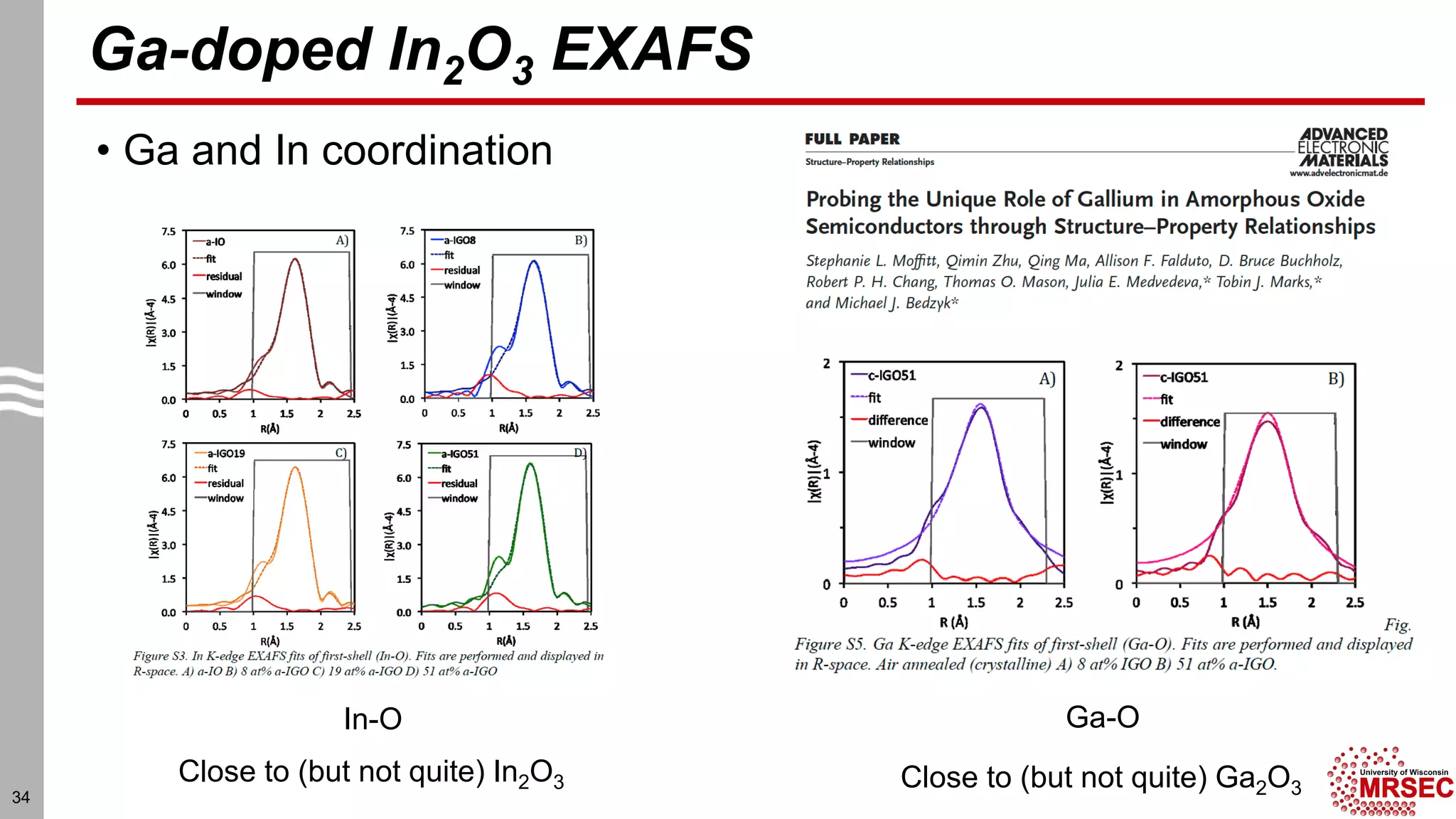
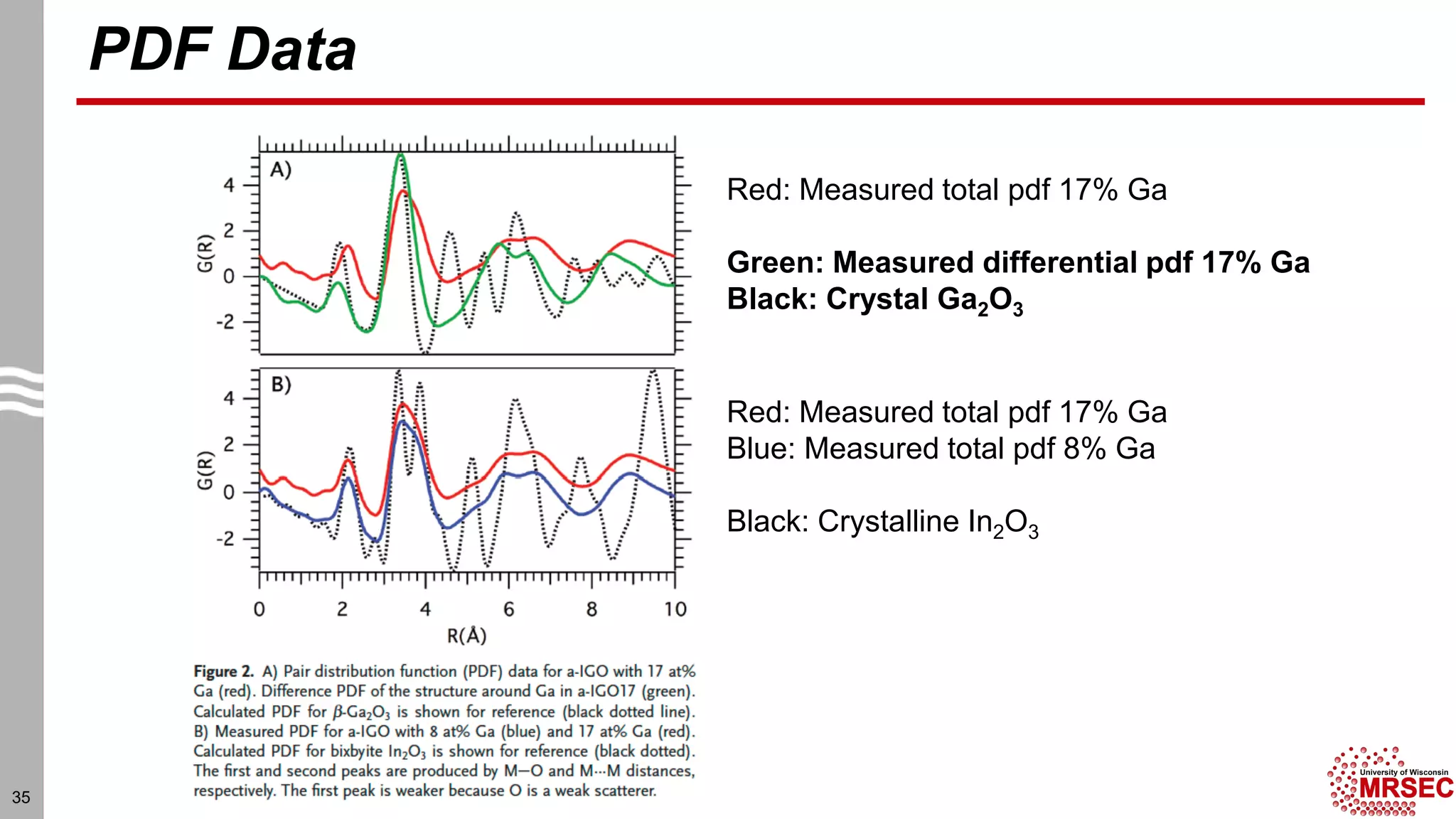
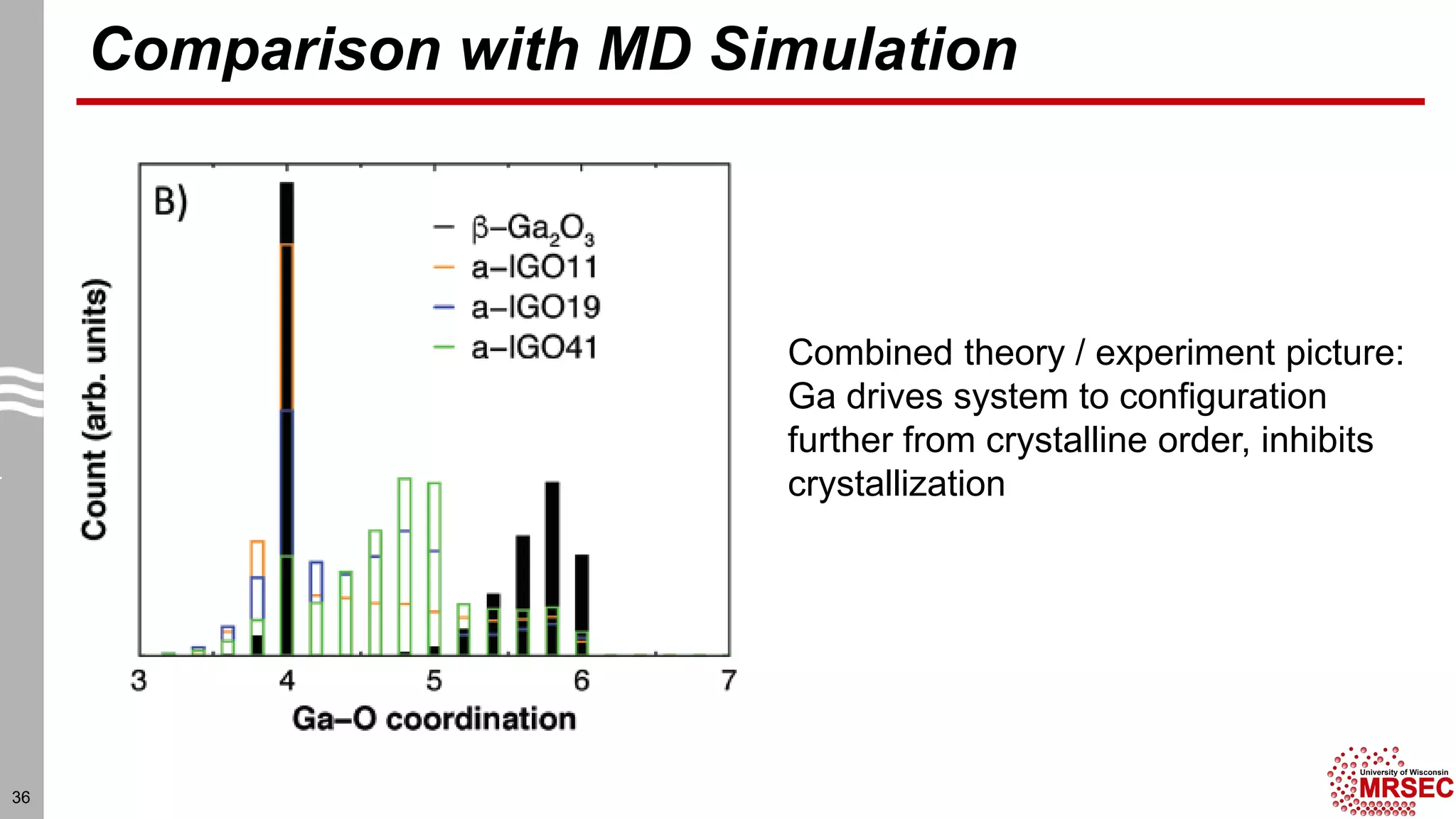
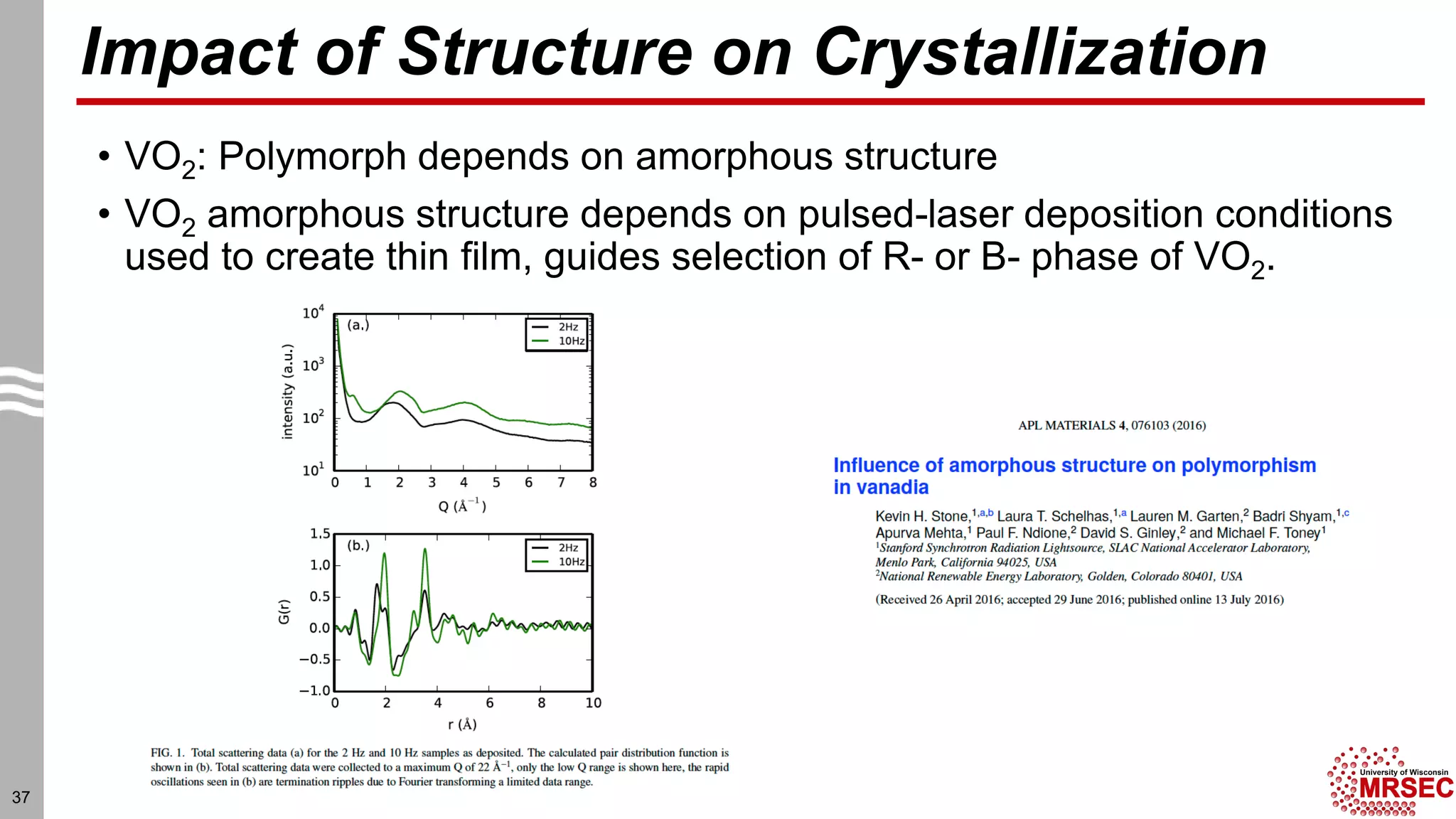
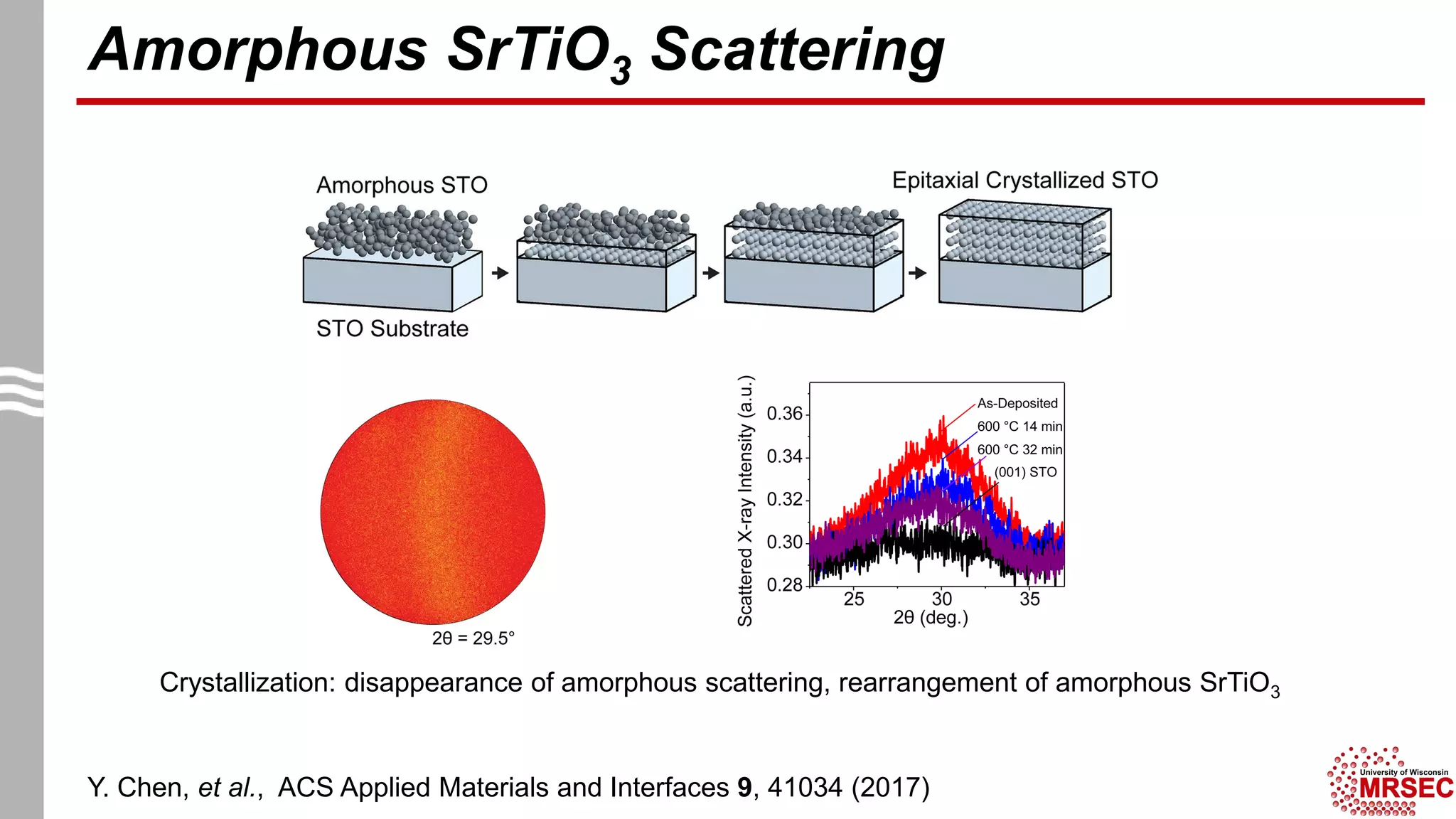
This document summarizes structural characterization techniques for amorphous materials. It discusses how amorphous materials have short-range order dominated by atomic bonding but no long-range translational order. Common characterization methods measure pair distribution functions to determine local structure. Structure varies between classes of amorphous materials like metallic glasses, molecular glasses, and covalent network glasses.

1. NSF Grant DMR-1720415
Amorphous Materials: Structural
Principles and Characterization
Paul M. Voyles and Paul G. Evans
Department of Materials Science and Engineering

2. Overview
• Basic structural features of amorphous
materials:
• short-range order dominated by atomic bonding
• no long-range translational order
• Common methods of structural characterization
for amorphous materials:
• variations on the theme of pair distribution functions
• Structure of various classes of amorphous
materials:
• metallic glasses
• molecular glasses
• covalent network glasses, especially silicates
• ionic amorphous solids, especially metal oxides
• Summary
2
https://go.wisc.edu/u2069r
Articles available at:

3. Common Structural Features of Amorphous Materials
• Short-range order:
• Nearest-neighbor atomic distances,
angles, coordination number, etc.
• Dominated by interatomic bonding
• Often similar to crystalline analogs
• No long-range translational symmetry
3
• No Bragg peaks in diffraction
covalent network
sphere packing

4. Goals of Structural Characterization
• Chemical state and coordination of component atoms/molecules
• Local and global structural order
• Impact of amorphous structure on stability, crystallization, and other
properties and processes
• Many tools available:
• X-ray scattering, diffraction, and spectroscopy
• Neutron diffraction
• Electron microscopy and scattering
• Raman spectroscopy
• Nuclear magnetic resonance
• Inelastic x-ray and neutron scattering
4

5. X-ray, Neutron, and Electron Scattering
• Measure scattered intensity as a function of direction
• Precise measurement, wide angular range
5

6. Structure Factor S(Q)
6
X-ray / neutron / electron scattering intensity depends directly on S(Q)
When data is very good:

7. Quantitative Relationship Between Experiment and g(r)
7
X-ray scattering intensity from arbitrary arrangement of atoms
Break into two contributions
Assume that amorphous sample is isotropic
𝐼𝐼 𝐐𝐐 = 𝑓𝑓 𝐐𝐐 2
�
𝑛𝑛
𝑒𝑒𝑖𝑖 𝐐𝐐⋅𝐫𝐫𝑛𝑛 �
𝑚𝑚
𝑒𝑒−𝑖𝑖 𝐐𝐐⋅𝐫𝐫𝑚𝑚 = 𝑓𝑓 𝐐𝐐 2
�
𝑛𝑛
�
𝑚𝑚
𝑒𝑒−𝑖𝑖 𝐐𝐐⋅ 𝐫𝐫𝑛𝑛−𝐫𝐫𝑚𝑚

8. Structure of Non-crystalline Materials
• Radial distribution function g(r): monatomic sample
• Caution: people go back and forth between “radial distribution
function” and pair distribution function. Also k and Q are often
switched!
8
= average atomic
number density
Als Nielsen and McMorrow Elements
of Modern X-ray Physics 2011

9. Radial Distribution Function
• Many possible statistical descriptions of scattering from non-periodic
materials.
• Simplest: Radial distribution function
• Determine from scattering pattern S(Q):
Non-periodic atomic
arrangement
Liquid Ni scattering pattern and r.d.f.Als Nielsen and McMorrow Elements
of Modern X-ray Physics 2011
9

10. Multi-ion Systems: Partial Structure Factor and
Partial Pair-Distribution Functions
10
Measuring Sαβ(Q) accurately is very hard! Not enough information
in I(Q).
Two ions α and β

11. Anomalous X-ray Scattering
11
• Example: GeSe and GeSe2
amorphous thin films
”Anomalous” scattering: use the idea that f(Q) depends on the x-ray photon energy.

12. Difference pdf “d-pdf”
12
KnownMeasurable
Strategy: Find Sαβ(Q), transform to find ραβ.

13. Amorphous Metals / Metallic Glasses
• Binary (at least) alloys which can be made
glassy by casting
• Cooling rates from 106 to ~1 K/s
• Applications driven by:
• high Young’s modulus at low weight
• good corrosion resistance
• biocompatibility
• high processability
• Cannot currently predict glass forming ability
of new alloys or design metallic glasses with
desired properties.
images from
Jan Schroers, Yale
Structure of Materials: an Introduction to Crystallography, Diffraction,
and Symmetry, Marc de Graef and Michael E. McHenry, Chapter 2113

14. Dense Random Packing
• Model for metallic liquids and
glasses as frozen liquids
• Treat metal atoms as hard
spheres:
• attractive potential up to some
bond distance r
• repulsive for shorter distance
• spherical symmetric
• Maximize the packing fraction
without introducing
crystallographic order
14
J. D. Bernal, Proc. R. Soc. Lond. A. Math. Phys.
Sci. 280, 299 (1964).
liquid Ar PDF
Bernal random model
Schott random model
ball bearings
in epoxy

15. Voronoi Polyhedron and Icosahedral Order
• Space closest to one atom
• Characteristic of nearest-neighbor
structures
• Icosahedron has only five-fold
rotational symmetries
• Non-crystallographically allowed
symmetry stabilizes metallic
liquids and glasses
15
2D
J. Tsai, N. Voss, M.
Gerstein, Bioinformatics.
17, 949–956 (2001).
3D
bcc fcc
<0 6 0 8> <0 12 0 0>
hcp
<0 6 0 2>
icosahedral atoms Voronoi polyhedron:
NPG Asia Mater. (2010),
doi:10.1038/asiamat.2010.51.
F. C. Frank, Proc. R. Soc. Lond. A.
Math. Phys. Sci. 215, 43 (1952)
indices <n3 n4 n5 n6>
are # of sides on the
polyhedron with n faces:
<0 0 12 0>

16. Varying Atomic Size and Efficient Packing
16
Y. Q. Cheng and E. Ma, Prog. Mater. Sci. 56, 379 (2011)
F. C. Frank and J. S. Kasper, Acta Crystallogr. 12, 483 (1959)
Frank-Kasper close-packed polyhedra atomic size ratio and preferred CNs
D. B. Miracle, W. S. Sanders, O. N.Senkov, Philos. Mag.
83, 2409 (2003)
T. Egami, Mater. Sci. Eng. A 226–228, 261–267 (1997)

17. Chemical Short-Range Order
• Neutron diffraction with isotope
substitution from Al87Ni7Nd6 glass
• Significant Ni-Ni ordering at 5 Å length
scale: Ni-Al-Ni
• Anomalous x-ray scattering at Ni K-
edge on La55Al25Ni20
• Strong ordering of La around Ni
17
K. Ahn, D. Louca, S. J. Poon, G. J. Shiflet,
Phys. Rev. B 70, 224103 (2004).
E. Matsubara, T. Tamura, Y. Waseda, T. Zhang, A. Inoue,
T. Masumoto, T. J. Non. Cryst. Solids 150, 380 (1992)
total RDF
Ni-centered
RDF
La-Ni
pairs

18. CSRO and Efficient Packing
• Solute-centered clusters:
• solvent shells determine by
packing efficiency
• 3rd atoms in interstitial spaces
• Few dominant “quasi-equivalent”
SRO cluster types for each glass
• Icosahedral and quasi-icosahedral
• Edge, face, and corner sharing
18 D. B. Miracle, Nat. Mater. 3, 697 (2004)
H. W. Sheng, W. K. Luo, F. M. Alamgir, J. M.
Bai, E. Ma, Nature 439, 419–25 (2006)

19. Non-icosahedral Glasses
• Mixtures of metal and “metalloid” atoms like B, C, Si, and P have
non-icosahedral short-range order
• Some directional bonding from the metalloid atoms
19
P. H. Gaskell, J. Non. Cryst. Solids 32, 207 (1979)
J. J. Maldonis and P. M. Voyles Arxiv: 1901.07014
Trigonal prism with connections for
generic metal-metalloid glass
Bi-capped square
antiprism in Pd-Si
Z9 Frank-Kasper
polyhedral in Ni-B
H. W. Sheng, W. K. Luo, F. M. Alamgir, J. M.
Bai, E. Ma, Nature 439, 419–25 (2006)

20. Nanodiffraction with Electrons
• Electron nanobeam diffraction:
one pattern at a time
• Fluctuation electron microscopy:
statistics of lots of patterns
20
DP_1 DP_2 DP_3 DP_4
A. Hirata, P. Guan, T. Fujita, Y. Hirotsu, A. Inoue, A. R.
Yavari, T. Sakurai, M. W. Chen, M. W. Nat. Mater. 10, 28
(2011)
A. Hirata, L. J. Kang, T. Fujita, B. Klumov, K. Matsue, M.
Kotani, A. R. Yavari, M. W. Chen, Science 341, 376 (2013)
M. M. J. Treacy, J. M. Gibson, L. Fan, D. J. Paterson,
I. McNulty, Reports Prog. Phys. 68, 2899 (2005)

21. Competing Icosahedral and Crystal-like Clusters
• Cluster with 6-fold rotational
symmetry, called “crystal-like”
• Chains of icosahedra, similar to
quasicrystals
21
<0 1 10 3>
<0 1 10 3>
<0 3 6 3>
<0 3 6 2>
<0 2 8 2>
<0 2 8 2>
<0 2 8 2>
<0 1 10 2>
<0 2 8 2>
<0 3 6 3>
<0 2 8 1>
<0 0 12 0>
<0 2 8 2>
J. Hwang, Z. Melgarejo, Y. E. Kalay, I.
Kalay, M .J. Kramer, D. S. Stone, P. M.
Voyles, Phys. Rev. Lett. 108, 195505 (2012)

22. Structure and Glass-Forming Ability
• Icosahedra in the liquid are
important in the glass transition
• Crystal-like clusters are important
to crystallization
22
Icosahedra
J. Ding, Y.-Q. Cheng, E. Ma, Acta Mater. 69, 343 (2014)
Y.-Q. Cheng, H. W. Sheng, E. Ma, PRB 78, 14207 (2008)
W. G. Stratton, Appl. Phys. Lett. 86, 141910 (2005)
P. Zhang Acta Mat 109, 103 (2016)
Good glass-former grows more icosahedral with
annealing. A poor glass former grows more crystal-like.

23. Structure and Plasticity
• Plastic deformation in metallic
glasses is inhomogeneous
• Localization into shear bands
makes most MGs globally brittle
• Simulations show that:
• deformation preferentially starts in
regions with low local five-fold
symmetry
• preferentially propagates between
regions of five-fold symmetry
• only penetrates those regions at
high strain
23 H. L. Peng Phys. Rev. Lett. 106, 135503 (2011)
red: regions of high non-affine strain
black: regions of high five-fold symmetry
Review: Schuh, C. A., Hufnagel, T. C. &
Ramamurty, U. Acta Mater. 55, 4067–4109 (2007).

24. Molecular Glasses
• Van der Walls bonds between
molecules
• Dense random packing of
non-spherical objects
• Hydrogen bonds between
molecules
• More directional bonding
network
24 Ediger, M. D., De Pablo, J. & Yu, L. Acc. Chem. Res. 52, 407 (2019)
rod-shaped: disc-shaped:
molecular model of amorphous ice

25. Globally Anisotropic Without Long-range Order
• Molecular glasses can have a preferred molecular orientation
without long-range order
25 Ediger, M. D., De Pablo, J. & Yu, L. Acc. Chem. Res. 52, 407 (2019)

26. Covalent Network Glasses
• Examples:
• Silica glasses
• Chalcogenides
• Amorphous silicon and germanium
• Structural hierarchy:
• directional bonds, bond angles, rings, clusters
• Statistics of geometry different from crystalline materials
• continuous random network
• network formers and network modifiers
• rings and topological clusters
• Modification via ionic substitution and doping
• coordination defects: over- and under-coordinated atoms
• constraint and rigidity theory: vibrational states / rigidity
transition, glass transition temp / viscosity
26
Amorphous Si
J. S. Lannin, Phys. Today 41, 7,
28 (1988)

27. Intuitive Relationship of Structure to Mechanical
Properties
27
Freely linked nearest-neighbor network Tree network
Mechanical properties predicted using geometry of network: viscosity, shear modulus
Extensions of this approach: dynamic reconfiguration of networks, jamming, complex statistical
mechanical considerations

28. Oxides: More Complex Building Blocks
• SiO2 Geometric Model: Corner
Sharing Tetrahedra
• Modifying and controlling this
network is the key to glass
technology
• Silica glasses: (e.g. Vogel Glass
Chemistry Springer 1994)
• Dopant rules and trends, specialized
geometric concepts, phase diagrams,
melting, optical properties
28

29. Structural Concepts in More General Oxide Glasses
29 Crystals: Repeats of octahedra, tetrahedra, etc.
Amorphous/Glass: Octahedra,
tetrahedra, but no long-range order
Short-range Glass Crystal

30. Some X-ray Scattering / Spectroscopy Examples
• Phosphate-based glasses
30
50% CaO 50% P2O5

31. Al2O3: Multiple Types of Polyhedral Connections
31
Corner-sharing tetrahedra
Edge-sharing tetrahedra

32. Amorphous Perovskites: SrTiO3 EXAFS
32
Ti Edge Sr Edge
Claim:
Tetrahedral Ti-O
coordination in
amorphous SrTiO3

33. Amorphous Ga-doped In2O3, Amorphous Semiconductor
• Charge carrier transport requires high crystallization T, depends
on Ga substitution
• Scattering: thin film is amorphous, crystallizes into doped In2O3
33

34. Ga-doped In2O3 EXAFS
• Ga and In coordination
34
In-O Ga-O
Close to (but not quite) In2O3 Close to (but not quite) Ga2O3

35. PDF Data
35
Red: Measured total pdf 17% Ga
Green: Measured differential pdf 17% Ga
Black: Crystal Ga2O3
Red: Measured total pdf 17% Ga
Blue: Measured total pdf 8% Ga
Black: Crystalline In2O3

36. Comparison with MD Simulation
36
Combined theory / experiment picture:
Ga drives system to configuration
further from crystalline order, inhibits
crystallization

37. 37
• VO2: Polymorph depends on amorphous structure
• VO2 amorphous structure depends on pulsed-laser deposition conditions
used to create thin film, guides selection of R- or B- phase of VO2.
Impact of Structure on Crystallization

38. Amorphous SrTiO3 Scattering
Crystallization: disappearance of amorphous scattering, rearrangement of amorphous SrTiO3
Y. Chen, et al., ACS Applied Materials and Interfaces 9, 41034 (2017)

39. Amorphous Complex Oxides
• No simple rule for the real-space interpretation of amorphous x-
ray scattering patterns from complex oxides
• Often combined with calculation to test structural models
• Combination of scattering with spectroscopic methods to
provide elemental sensitivity
39

40. Summary
• Amorphous solids lack long-range translational order, but often have
strong short-range order
• Short-range order is controlled by interatomic bonding:
• packing efficiency for spherical bonds (metals and molecules)
• directional bond networks for covalent and hydrogen bonds (silicates and
water)
• preferred polyhedral for ionic bonds (metal oxides)
• Short-range structure in an amorphous solid often mimics structure
of corresponding crystals
• Lots of ways to characterize amorphous structures with experiments
and simulations.
• Structure impacts crystallization, stability in the amorphous state,
mechanical, electronic, and other properties.
40