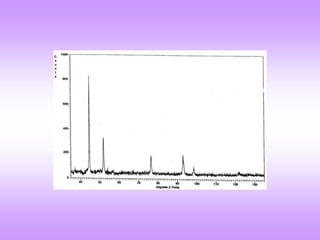
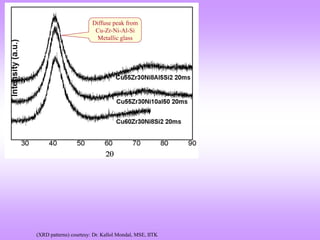
X-ray diffraction is a technique used to analyze the crystal structure of materials. It works by firing X-rays at a crystalline sample. The X-rays cause the electrons in the material to oscillate, re-radiating the electromagnetic waves. These waves undergo constructive and destructive interference based on Bragg's law, which states that for diffraction to occur, the path difference between waves must equal an integer multiple of the wavelength. This produces a diffraction pattern that can be analyzed to determine information about the crystal structure such as the lattice type and parameters. Other signals produced during XRD include fluorescent X-rays and electrons ejected from the material.

1. X-RAY DIFFRACTION
 X- Ray Sources
 Diffraction: Bragg’s Law
 Crystal Structure Determination
Elements of X-Ray Diffraction
B.D. Cullity & S.R. Stock
Prentice Hall, Upper Saddle River (2001)
Recommended websites:
 http://www.matter.org.uk/diffraction/
 http://www.ngsir.netfirms.com/englishhtm/Diffraction.htm
MATERIALS SCIENCE
&
ENGINEERING
Anandh Subramaniam & Kantesh Balani
Materials Science and Engineering (MSE)
Indian Institute of Technology, Kanpur- 208016
Email: anandh@iitk.ac.in, URL: home.iitk.ac.in/~anandh
AN INTRODUCTORY E-BOOK
Part of
http://home.iitk.ac.in/~anandh/E-book.htm
A Learner’s Guide
Caution Note: In any chapter, amongst the first few pages (say 5 pages) there will be some ‘big picture’
overview information. This may lead to ‘overloading’and readers who find this ‘uncomfortable’ may skip
particular slides in the first reading and come back to them later.
X-Ray Diffraction: A Practical Approach
C. Suryanarayana & M. Norton Grant
Plenum Press, New York (1998)
A very good book for
practical aspects

2.  How to produce monochromatic X-rays?
 How does a crystal scatter these X-rays to
give a diffraction pattern?
 Bragg’s equation
 What determines the position of the XRD
peaks?  Answer) the lattice.
 What determines the intensity of the XRD
peaks?  Answer) the motif.
In a powder pattern (or a given experimental setup) there
are many other factors which contribute to the intensity of
a given peak.
What will you learn in this ‘sub-chapter’? Other relevant topics
Laue_picture.ppt
line_broadening.ppt
other_signals_xray.ppt
reciprocal_lattice.ppt
structure_factor_calculations.ppt
Understanding_diffraction.ppt
XRD_lattice_parameter_calculation.ppt
XRD_powder_diffraction.ppt
XRD_sample_patterns.ppt
 How to analyze a powder pattern to get information about the lattice type?
(Cubic crystal types).
 What other uses can XRD be put to apart from crystal structure determination?
 Grain size determination  Strain in the material  Determination of solvus line in phase
diagrams.

3.  For electromagnetic radiation to be diffracted* the spacing in the grating ( grating refers to
a series of obstacles or a series of scatterers) should be of the same order as the wavelength.
 In crystals the typical interatomic spacing ~ 2-3 Å**  so the suitable radiation for the
diffraction study of crystals is X-rays.
 Hence, X-rays are used for the investigation of crystal structures.
 Neutrons and Electrons are also used for diffraction studies from materials.
 Neutron diffraction is especially useful for studying the magnetic ordering in materials.
 Lasers can be used for optical diffraction, when the spacing between the scatterers involved
is much larger (~m, e.g. in optical diffraction grating).
 In diffraction we are interested in the elastic interaction of waves with matter.
Some Basics
** Lattice parameter of Cu (aCu) = 3.61 Å
 dhkl is equal to aCu or less than that (e.g. d111 = aCu/3 = 2.08 Å)
** If the wavelength is of the order of the lattice spacing, then diffraction effects will be prominent.
 Three possibilities (regimes) exist based on the wavelength () and the spacing between the scatteres (a).
  < a  transmission dominated.
  ~ a  diffraction dominated.
  > a  reflection dominated.
Click here to know more about this
Click here to know more

4. Beam of electrons Target
X-rays
An accelerating (or decelerating) charge radiates electromagnetic radiation
 X-rays can be generated by decelerating electrons.
 This is achived by bombarding a target (say Cu) with an electron beam.
 The resultant spectrum of X-rays generated (i.e. X-rays versus Intensity plot) consists of
intense peaks on a ‘continuous/broad’ background.
 The intense peaks can be ‘utilized’ as monochromatic radiation and be used for X-ray
diffraction studies.
Generation of X-rays

5. Intensity
Wavelength ()
0.2 0.6 1.0 1.4
White
radiation
Characteristic radiation →
due to energy transitions
in the atom
K
K
Intense peak, nearly
monochromatic
Mo Target impacted by electrons accelerated by a 35 kV potential shows the emission spectrum as
in the figure below (schematic).
The ‘white radiation’ or the continuous radiation is typically not used in XRD studies.
 The high intensity nearly monochromatic K x-rays can be used as a radiation source for X-ray
diffraction (XRD) studies. The term ‘nearly’ has been used as the K has a combination of K1 and K2 ‘lines’ and there are other
sources of broadening.
 A monochromator can be used to further decrease the spread of wavelengths in the X-ray
beam.
X-ray sources with different  for
doing XRD studies
Target
Metal
 Of K
radiation (Å)
Mo 0.71
Cu 1.54
Co 1.79
Fe 1.94
Cr 2.29

6. Elements (KV)  Of K1
radiation (Å)
 Of K2
radiation (Å)
 Of Kβ
radiation (Å)
Kβ-Filter
(mm)
Ag 25.52 0.55941 0.5638 0.49707 Pd (0.0461)
Mo 20 0.7093 0.71359 0.63229 Zr (0.0678)
Cu 8.98 1.540598 1.54439 1.39222 Ni (0.017)
Ni 8.33 1.65791 1.66175 1.50014 Co (0.0158)
Co 7.71 1.78897 1.79285 1.62079 Fe (0.0166)
Fe 7.11 1.93604 1.93998 1.75661 Mn (0.0168)
Cr 5.99 2.2897 2.29361 2.08487 V (0.169)
C. Gordon Darwin, Grandson of C. Robert Darwin developed the dynamic theory of scattering of x-rays (a tough theory!) in 1912
X-ray sources with different  for doing XRD studies

7. X-rays can also be refracted (refractive index slightly less than 1) and reflected (at very small angles)
 When X-rays impinge on a specimen, the interaction can result in various signals/emissions/
effects.
 The coherently scattered X-rays are the ones important from a XRD perspective.
 The interaction of the incident X-rays with loosely bound charges leads to incoherent
scattering of X-rays (also refered to as Compton modified X-rays).
 The incident X-rays may knock off of a core level electron of atoms of the material, followed
by the transition of an electron from a higher level. This leads to the emission of ‘secondary’
X-rays the fluorescent X-rays.
 Incident X-rays may also knock out electrons from the material (Compton recoil and
photoelectrons).
Absorption (Heat)
Incident X-rays
SPECIMEN
Transmitted beam
Fluorescent X-rays Electrons
Compton recoil Photoelectrons
Scattered X-rays
Coherent
From bound charges
Incoherent (Compton modified)
From loosely bound charges
Click here to know more
Useful for XRD studies

8.  Now we shall consider the important topic as to how X-rays interact with a
crystalline array (of atoms, ions etc.) to give rise to the phenomenon known as X-
ray diffraction (XRD).
 Let us consider a special case of diffraction → a case where we get ‘sharp[1]
diffraction peaks’.
 Diffraction (with sharp peaks) (with XRD being a specific case) requires three important conditions to
be satisfied:
Radiation related Coherent, monochromatic, parallel waves& (with wavelength ).
Sample related Crystalline array of scatterers* with spacing of the order of (~) .
Diffraction geometry related Fraunhofer diffraction geometry (& this is actually part of the Fraunhofer geometry)
[1] The intensity- plot looks like a ‘’function (in an ideal situation).
* A quasicrystalline array will also lead to diffraction with sharp peaks (which we shall not consider in this text).
** Amorphous material will give broadened (diffuse) peak (additional factors related to the sample can also give a broad peak).
Diffraction Click here to “Understand Diffraction”
Coherent, monochromatic, parallel wave
Fraunhofer geometry
Diffraction pattern
with sharp peaks
Crystalline*,**
Aspects related to the wave
Aspects related to the material
Aspects related to the diffraction set-up
(diffraction geometry)

9.  The waves could be:
 electromagnetic waves (light, X-rays…),
 matter waves** (electrons, neutrons…) or
 mechanical waves (sound, waves on water surface…).
 Not all objects act like scatterers for all kinds of radiation.
 If wavelength is not of the order of the spacing of the scatterers, then the number of peaks
obtained may be highly restricted (i.e. we may even not even get a single diffraction peak!).
 In short diffraction is coherent reinforced scattering (or reinforced scattering of coherent waves).
 In a sense diffraction is nothing but a special case of constructive (& destructive)
interference.
To give an analogy  the results of Young’s double slit experiment is interpreted as interference, while the result of
multiple slits (large number, diffraction grating) is categorized under diffraction.
 Fraunhofer diffraction geometry implies that parallel waves are impinging on the scatterers
(the object), and the screen (to capture the diffraction pattern) is placed far away from the
object.
** With a de Broglie wavelength
Some comments and notes
Click here to know more about Fraunhofer and Fresnel diffraction geometries

10. Sets Electron cloud into oscillation
Sets nucleus into oscillation
Small effect  neglected
 A beam of X-rays directed at a crystal interacts with the electrons of the atoms in the crystal.
 The electrons oscillate under the influence of the incoming X-Rays and become secondary sources
of EM radiation.
 The secondary radiation is in all directions.
 The waves emitted by the electrons have the same frequency as the incoming X-rays  coherent.
 The emission can undergo constructive or destructive interference.
XRD  the first step
Schematics
Incoming X-rays
Secondary
emission
Oscillating charge re-radiates  In phase with
the incoming x-rays

11.  We can get a better physical picture of diffraction by using Laue’s formalism* (leading to the Laue’s
equations).
 However, a parallel approach to diffraction is via the method of Bragg, wherein diffraction can be
visualized as ‘reflections’ from a set of planes.
 As the approach of Bragg is easier to grasp we shall use that in this elementary text.
 We need to do some intriguing mental experiments to utilize the Bragg’s equation (Bragg’s model)
with caution.
 Let us consider a coherent wave of X-rays impinging on a crystal with atomic planes at an
angle  to the rays.
 Incident and scattered waves are in phase if the:
i) in-plane scattering is in phase and
ii) scattering from across the planes is in phase.
Incident and scattered
waves are in phase if
Scattering from across planes is in phase
In plane scattering is in phase
Some points to recon with ...
 *Max von Laue’s postulate: If (i) crystals have a periodic arrangement of atoms and if
(ii) x-rays of waves (concepts which were not confirmed till then), then crystals should act
like a diffraction grating for x-rays. Both these postulates (i & ii) were proved by a single
experiment by Laue (published in 1912 which won him the noble prize in 1914).
A Laue diffraction pattern
with ‘sharp’ peaks.

12. Extra path traveled by incoming waves  AY
A B
X Y
Atomic Planes
Extra path traveled by scattered waves  XB
These can be in phase if
 incident = scattered
A B
X Y
But this is still reinforced scattering
and NOT reflection
Let us consider in-plane scattering
There is more to this
Click here to know more and get
introduced to Laue equations describing
diffraction

13. BRAGG’s EQUATION
 A portion of the crystal is shown for clarity- actually, for destructive interference to occur
many planes are required (and the interaction volume of x-rays is large as compared to that shown in the schematic).
 The scattering planes have a spacing ‘d’.
 Ray-2 travels an extra path as compared to Ray-1 (= ABC). The path difference between
Ray-1 and Ray-2 = ABC = (d Sin + d Sin) = (2d.Sin).
 For constructive interference, this path difference should be an integral multiple of :
n = 2d Sin  the Bragg’s equation. (More about this sooner).
 The path difference between Ray-1 and Ray-3 is = 2(2d.Sin) = 2n = 2n. This implies that if Ray-1
and Ray-2 constructively interfere Ray-1 and Ray-3 will also constructively interfere. (And so forth).
Let us consider scattering across planes
Click here to visualize
constructive and
destructive interference
See Note Ӂ later
Warning: we are using ray diagrams in spite of
being in the realm of ‘physical optics’
Path difference between
Ray-1 & Ray-2

14. Click here to understand how
destructive interference of
just ‘of-Bragg rays’ occur
Interference of ‘Ray-1’ with ‘Ray-2’
Note that they ‘almost’constructively interfere!
Which remains same
thereafter (like in the
BB’ plane)
 The previous page explained how constructive interference occurs.
 How about the rays just of Bragg angle? Obviously the path difference would be just off  as
in the figure below. This will not lead to complete destructive interference and hence this ‘ray’
should exist !
 How come these “rays”, which are just of the Bragg angle, ‘go missing’?
The explanation can be found in the link: understanding diffraction.
 Briefly, as we go deeper into the crystal we will accrue path differences and the ray from
plane-1 will be exactly out of phase (path difference of /2) with a ray scattered from this
‘deep seated plane’ and hence will ‘go missing’.

15. How to ‘see’ that path difference increases with angle?
Clearly A’BC’ > ABC
Q & A

16. Laue versus Bragg*
 In Laue’s picture constructive and destructive interference at various points in space is
computed using path differences (and hence phase differences) given a crystalline array of
scatterers.
 Bragg simplified this picture by considering this process as ‘reflections from atomic planes’.
(More about the Bragg’s viewpoint soon). Click here to know more about the Laue Picture
“The important thing in science is not so much to obtain new facts as to discover
new ways of thinking about them”. William Lawrence Bragg.
 *Sir William Henry Bragg and William Lawrence Bragg (this won the father and son team the noble prize in
1915).
[1] http://www.nobelprize.org/nobel_prizes/physics/laureates/1915/index.html
[1]
[1]
Since there are two Braggs involved, wherever we
refer to the law or the equation it has be Braggs’ (and
not Bragg’s as I have done in this chapter)

17. Reflection versus Diffraction
Reflection Diffraction
Occurs from surface
Occurs throughout the bulk
(though often the penetration of x-rays in only of the
order of 10s of microns in a material)
Takes place at any angle Takes place only at Bragg angles
~100 % of the intensity may be reflected Small fraction of intensity is diffracted
Note: X-rays can ALSO be reflected at very small angles of incidence
 Though diffraction (according to Bragg’s picture) has been visualized as a reflection from a
set of planes with interplanar spacing ‘d’  diffraction should not be confused with
reflection (specular reflection).
Planes are imaginary constructs
If n = 2d Sin is the Bragg’s equation, then what is the (famous) Braggs’ law?
Braggs Law
 The diffracted beam appears to be specularly reflected from a set of crystal lattice planes.
 Angle of incidence = Angle of reflection.
Quantum
Jump

18.  n = 2d Sin
The equation is written better with some descriptive subscripts:
 n is an integer and is the order of the reflection
(i.e. how many wavelengths of the X-ray go on to make the path difference between planes).
Note: if hkl reflection (corresponding to n=1) occurs at hkl then 2h 2k 2l reflection (n=2) will occur at a higher angle 2h 2k 2l.
 Bragg’s equation is a negative statement
 If Bragg’s eq. is NOT satisfied  NO ‘reflection’ can occur
 If Bragg’s eq. is satisfied  ‘reflection’ MAY occur
(How?- we shall see this a little later).
 The interplanar spacing appears in the Bragg’s equation, but not the interatomic
spacing ‘a’ along the plane (which had forced incident = scattered); but we are not
free to move the atoms along the plane ‘randomly’  click here to know more.
  For large interplanar spacing the angle of reflection tends towards zero → as d increases, Sin
decreases (and so does ).
 The smallest interplanar spacing from which Bragg diffraction can be obtained is /2 →
maximum value of  is 90, Sin is 1  from Bragg equation d = /2.
Understanding the Braggs’ equation
( )
2 Sin
Cu K hkl hkl
d
n 
 
 If this equation is satisfied, then  is Bragg
Note: Ӂ
( )
2 Sin Bragg
CuK hkl hkl
n d

 

This (hkl) is in real space and hence the brackets we will soon drop this brackets!

19.  For Cu K radiation ( = 1.54 Å) and d110= 2.22 Å
n Sin = n/2d 
1 0.34 20.7º • First order reflection from (110)  110
2 0.69 43.92º
• Second order reflection from (110) planes  110
• Also considered as first order reflection from (220) planes  220
( ) 2 2 2
Cubic crystal
hkl
a
d
h k l

 
(220)
8
a
d 
(110)
2
a
d 
2
1
110
220

d
d
Relation between dnh nk nl and dhkl e.g.
( ) 2 2 2
( ) ( ) ( )
nhnk nl
a
d
nh nk nl

  2 2 2
hkl
nhnk nl
d
a
d
n
n h k l
 
 
Order of the reflection (n)
110
220
2
d
d 
( )
2 hkl hkl
d Sin
n 

In XRD nth order reflection from (h k l) is “considered” as 1st order reflection from (nh nk nl).
(hkl)
hkl
d
λ=2 Sinθ
n
( )
( )
1
nhnk nl
hkl
d
d n

 
( )
2 nh nk nl nh nk nl
d Sin
 

Alternate way of writing
Bragg’s equation
 Note: the ‘n’is “absorbed” both in the ‘d’and the .
 We explicitly write  nh nk nl to show that this reflection occurs at a different angle (higher angle as compared to  h k l ).

20. 300
100
1
3
d
d

200
100
1
2
d
d

Hence, (100) planes are a
subset of (200) planes
Important point to note:
In a simple cubic crystal, 100, 200, 300… are all allowed ‘reflections’. But, there are no atoms in the
planes lying within the unit cell! Though, first order reflection from 200 planes is equivalent
(mathematically) to the second order reflection from 100 planes; for visualization purposes of
scattering, this is better thought of as the later process (i.e. second order reflection from (100) planes).
Note:
Technically, in Miller indices we factor out the common factors. Hence, (220)  2(110)  (110).
In XRD we extend the usual concept of Miller indices to include planes, which do not pass through
lattice points (e.g. every alternate plane belonging to the (002) set does not pass through lattice points)
and we allow the common factors to remain in the indices.
All these form the (200) set

21. I have seen diagrams like in Fig.1 where rays seem to be scattered from nothing!
What does this mean?
Funda Check
 Few points are to be noted in this context. The ray ‘picture’ is only valid in the realm of geometrical
optics, where the wave nature of light is not considered (& also the discrete nature of matter is
ignored; i.e. matter is treated like a continuum). In diffraction we are in the domain of physical optics.
 The wave impinges on the entire volume of material including the plane of atoms (the effect of which
can be quantified using the atomic scattering power* and the density of atoms in the plane). Due to the
‘incoming’ wave the atomic dipoles are set into oscillation, which further act like emitter of waves
 In Bragg’s viewpoint, the atomic planes are to be kept in focus and the wave (not just a ray) impinges
on the entire plane (some planes have atoms in contact and most have atoms, which are not in contact
along the plane  see Fig.2).
* To be considered later
A plane in Bragg’s viewpoint can be characterized by two factors: (a) atomic density (atoms/unit area on the plane), (b) atomic scattering
factor of the atoms.
Fig.1
Fig.2
Wave impinging on a crystal (parallel wave-front). (Note there are no ‘rays’. A vector drawn normal to the wave-front,
in the direction of propagation can be considered as the ray)
??

22.  “It is difficult to give an explanation of the nature of the semi-transparent layers or planes
that is immediately convincing, as they are a concept rather than a physical reality.
Crystal structures, with their regularly repeating patterns, may be referred to a 3D grid and
the repeating unit of the grid, the unit cell, can be found. The grid may be divided up into
sets of planes in various orientations and it is these planes which are considered in the
derivation of Bragg’s law. In some cases, with simple crystal structures, the planes also
correspond to layers of atoms, but this is not generally the case. See Section 1.5 for further
information. [1]
 Some of the assumptions upon which Bragg’s law is based may seem to be rather dubious.
For instance, it is known that diffraction occurs as a result of interaction between X-rays
and atoms. Further, the atoms do not reflect X-rays but scatter or diffract them in all
directions. Nevertheless, the highly simplified treatment that is used in deriving Bragg’s
law gives exactly the same answers as are obtained by a rigorous mathematical treatment.
We therefore happily use terms such as reflexion (often deliberately with this alternative,
but incorrect, spelling!) and bear in mind that we are fortunate to have such a simple and
picturesque, albeit inaccurate, way to describe what in reality is a very complicated
process.” [1]
[1] Anthony R West, Solid State Chemistry and its Applications, Second Edition, John Wiley & Sons Ltd., Chichester, 2014.
More about the Bragg’s viewpoint

23. How is it that we are able to get information about lattice parameters of the order
of Angstroms (atoms which are so closely spaced) using XRD?
Funda Check
 Diffraction is a process in which
‘linear information’(the d-spacing of the planes)
is converted to ‘angular information’(the angle of diffraction, Bragg).
 If the detector is placed ‘far away’ from the sample (i.e. ‘R’ in the figure below is large) the
distances along the arc of a circle (the detection circle) get amplified and hence we can make
‘easy’ measurements.
 This also implies that in XRD we are concerned with angular resolution instead of linear
resolution.
Later we will see that in powder
diffraction this angle of deviation (2) is
plotted instead of .
Note: angular variations lead to phase and
path differences.

24. Forward and Back Diffraction
 Here a guide for quick visualization of forward and backward scattering (diffraction) is
presented.
 Diffraction angles less than 45 correspond to forward diffraction.
* Only one plane of the set is drawn in most cases.

25. Funda Check
What is  (theta) in the Bragg’s equation?
  is the angle between the incident X-rays and
the set of parallel atomic planes (which have a
spacing dhkl).
 Usually,  in this context implies Bragg (i.e.
the angle at which Bragg’s equation is
satisfied).
 It is NOT the angle between the X-rays and
the sample surface (note: specimens could be
irregular & could have a rough surface).
 It is also not the angle between the plane
‘normal’* and the incident ‘rays’ this is the
angle usually considered in geometrical optics
(reflection, refraction,...).
 In the figure the sample has a irregular
boundary and consists of many crystallites (or
grains).
 Each of these crystallites have an infinite
number of lattice planes.
 The incident rays form an angle  w.r.t to the
(13) planes for the chosen crystallite (which is
now the Bragg’s angle).
 The (13) plane in other crystallites may not be
favourably oriented for Bragg diffraction.
Another view, where the
(13) plane is shown in
all the crystals
* Usually, the ‘plane’in optics is the sample surface (also, the sample is
usually a glass). E.g. refraction through as prism.

26. What do the terms ‘sharp’ and ‘diffuse’ mean with regard to peaks and scattering?
Funda Check
 Sharp peaks are obtained from crystalline materials (using parallel, monochromatic
radiation), while typically a broad peak is obtained from an amorphous material. The sharp
peak is referred to as a Bragg peak.
 Defects (like point defects, thermal vibration, partial ordering) in the crystal can give rise to
low intensity scattering between the Bragg peaks. This is termed as diffuse scattering.
SAD pattern (TEM ) from the
amorphous sample
XRD pattern showing the formation of amorphous
structure in the suction cast (Cu64Zr36)96Al4 alloy
Note the broad peak

27.  We had mentioned that Bragg’s equation is a negative statement: i.e. just because Bragg’s
equation is satisfied a ‘reflection’ may not be observed.
 Let us consider the case of Cu K radiation ( = 1.54 Å) being diffracted from (100) planes
of Mo (BCC, a = 3.15 Å = d100).
The missing ‘reflections’
100 100
2d Sin
 
 100
100
1.54
0.244
2 2(3.15)
Sin
d

    100 14.149
   But this reflection is
absent in BCC Mo
The missing reflection is due to the
presence of additional atoms in the unit
cell (which are positions at lattice
points)  which we shall consider next.  The wave scattered from the middle plane is out
of phase with the ones scattered from top and
bottom planes. I.e. if the green rays are in phase
(path difference of ) then the red ray will be
exactly out of phase with the green rays (path
difference of /2).
 The scattering power of these two planes (the
green and the red) are identical, as both the
planes contain the same atom and have 1 atom
per a2 area.
This ‘issue’ arises because so far we have talked
about (hkl) planes and nothing about atoms on
those planes or within the unit cell.

28. However, the second order reflection from (100) planes (which is equivalent to the first order reflection
from the (200) planes) is observed.
100
100
2 1.54
0.48
2 3.15
Sin
d

    2 1
100 200
~ 29.26
nd nd
order order
   
This is because if the green rays have a path difference of 2 then the red ray will have path
difference of → which will still lead to constructive interference!
Continuing with the case of BCC Mo…
Why does the 110 reflection not go missing? (Why is it present?)
Funda Check
Let us look at the (110) planes in projection.
Note that (110)blue coloured planes existed before and after introducing an
atom at unit cell centre at (½, ½ ½)grey coloured. Thus lattice centering
does not lead to any waves being scattered out of phase.

29.  Presence of additional atoms/ions/molecules in the UC
 at lattice points (as we may chose a non-primitive unit cell)
 or as a part of the motif
can alter the intensities of some of the reflections.
 Some of the reflections may even go missing.
Important
points
 Position of the ‘reflections’/‘peaks’ tells us about the lattice type.
 The Intensities tells us about the motif.
Lattice point

30. Intensity of the Scattered Waves
Electron
Atom
Unit cell (uc)
Scattering by a crystal can be understood in three steps
A
B
C
Polarization factor
Atomic scattering factor (f)
Structure factor (F)
To understand the scattering from a crystal leading to the
‘intensity of reflections’ (and why some reflections go
missing), three levels of scattering have to be considered:
1) scattering from electrons
2) scattering from an atom
3) scattering from a unit cell
Click here to know the details
Structure factor calculations
&
Intensity in powder patterns
 Structure Factor (F): The resultant wave scattered
by all atoms of the unit cell
 The Structure Factor is independent of the shape
and size of the unit cell; but is dependent on the
position of the atoms/ions etc. within the cell
Click here to know more about
 Bragg’s equation tells us about the position of the diffraction peaks (in terms of )  but
tells us nothing about the intensities. The intensities of the peaks depend on many factors as
considered here.

31. The concept of a Reciprocal lattice and the Ewald Sphere construction:
 Reciprocal lattice and Ewald sphere constructions are important tools towards understanding
diffraction.
(especially diffraction in a Transmission Electron Microscope (TEM))
 A lattice in which planes in the real lattice become points in the reciprocal lattice is a very
useful one in understanding diffraction.
 Structure factor calculations give us the intensities which decorate the reciprocal lattice to
give us the reciprocal crystal.
 click here & here to go to a detailed description of these topics.
Reciprocal Lattice & Ewald Sphere construction
Click here to know more about
Structure Factor Calculations
Click here to know more about

32. Bravais Lattice* Reflections which may be present Reflections necessarily absent
Simple All None
Body centred (h + k + l) even (h + k + l) odd
Face centred h, k and l unmixed (i.e. all even or all odd) h, k and l mixed
End centred (C centred) h and k unmixed (centering along ‘l’index) h and k mixed
Structure Allowed Reflections
SC crystal All
BCC crystal (h + k + l) even
CCP crystal h, k and l unmixed
DC crystal
Either,  h, k and l are all odd or
 all are even & (h + k + l) divisible by 4
Selection / Extinction Rules
 As we have noted before even if Bragg’s equation is satisfied, ‘reflections may go missing’
 this is due to the presence of additional atoms in the unit cell.
These atoms may be present at ‘additional’ lattice sites or as a part of the motif. In the case of DC crystal, in addition to the
restrictions/conditions imposed for the FCC lattice, further conditions/restrictions are imposed due to presence of atoms as a part of the motif.
 The reflections present and the missing reflections due to additional atoms in the unit cell are
listed in the table below.
Click here to see the derivations of selection rules: Structure factor calculations
* Note that the lattice has to be decorated with ‘atomic species’for diffraction to actually occur (lattices by themselves do not
give Bragg diffraction !!!!).
Additional atoms at lattice positions
Additional atoms w.r.t FCC
lattice as a part of the motif.

33. h2 + k2 + l2 SC FCC/CCP BCC DC
1 100
2 110 110
3 111 111 111
4 200 200 200
5 210
6 211 211
7
8 220 220 220 220
9 300, 221
10 310 310
11 311 311 311
12 222 222 222
13 320
14 321 321
15
16 400 400 400 400
17 410, 322
18 411, 330 411, 330
19 331 331 331
Allowed reflections in
SC*, CCP, BCC* &
DC crystals
* lattice decorated with
monoatomic/monoionic motif
Cannot be expressed as (h2+k2+l2)
Note these reflections were present in CCP

34. Allowed reflections in
HCP crystals
Reflections which may be present Reflections necessarily absent
l even, (h+2k)  3n l odd, (h+2k) = 3n

35. Q & A What happens to the reflections? (i) BCC: 111BCC. (ii) FCC: 100, 110, 111, 200. (iii)
DC: 100, 110, 200.
 BCC.
 111. On introducing the atom at the body centre a new orange atomic plane/hexagon is created. This plane is exactly
midway between the blue and green planes. The difficult part is to fathom out the atomic density of this plane. The
green plane is made of 4 smaller  and it contains ½ an atom (3  1/6). The orange plane is not space filling and
coupled with the maroon triangles becomes so. Each maroon triangle is shared between 3 orange hexagons and hence
the part belonging to each orange hexagon is 6  1/3 = 2. The hexagon is itself made of 6 and contains 1 atom. So
the planar density is 1 atom per (6+2).
Given that the atomic densities of these planes are identical, it implies that the 111 reflection will go missing.
 Missing.
Green plane has
1
2 1
4 8
atom atom

 
Continued…
The mid plane is made of one orange hexagon and a maroon  shared
between 3 hexagons. Hence, the atomic density is 1 1
6 2 8
atom atom

   
The symbol  refers to one small triangle
Atoms/area

36.  FCC.
 100. Fig.1. On introducing face centering lattice positions, a new orange plane is created exactly midway between
the green and the blue planes. The atomic density of all these planes are 2 atoms per a2.  Missing.
 110. Fig.2. When we introduce face centring atoms (orange colour), some of these sit on the original (110) planes
(grey lines in projection), while new planes (orange lines in projection) also created, which are midway
between the grey planes. The atomic density of the grey planes are 2 atoms per a22 area. The area of the
orange planes are 1 atom per a22/2 area (i.e. identical to the grey planes).  Missing.
 111. Fig.3. When we introduce atoms at face centres, these lie on pre-existing planes (the blue and green planes);
hence, the 111 reflection will be present in FCC crystals.  Present.
 200. Fig.4. The 200 reflection is the 2 reflection from the 100 planes. This implies that the path difference between
the grey planes is one  and hence this will be present.  Present.
Grey plane has
2
2
2
atoms
a
Orange plane has
2 2
2
2
1 2
2
a
atoms atoms
a

Fig.1 (100)
Continued…
Fig.2 (110)
Fig.3 (111)
Fig.4 (200)

37.  DC.
For DC we can start with the selection rules for FCC and further work out the effect of an additional atom, which is part
of the motif. This implies that 100 and 110 reflections will be missing.
 100. Missing as per the rules of the FCC lattice.  Missing.
 110. Missing as per the rules of the FCC lattice.  Missing.
 200. This reflection is present in the FCC lattice, but now we have to consider the effect of the additional atoms,
which are part of the motif. The grey planes scatter in phase (the 200 planes). On the introduction of orange
atoms at (¼. ¼, ¼) and equivalent positions a new plane has to be drawn. This plane will scatter exactly out of
phase (/2) with the grey planes and hence the 200 reflection will be missing in the DC structure.  Missing.
Path difference accrued

38. Q & A How do we get the lattice parameter of a cubic crystal from a XRD experiment?
 The broad process followed to ‘go from’ a cubic crystal to get lattice parameters is as below.
Crystal with atoms
2 information (Intensity-2 plot)
Get ‘a’ (lattice parameter)
Get ‘d’ spacing
Get lattice type (SC, BCC, FCC,...)
Diffraction experiment
( )
2 Sin Bragg
CuK hkl hkl
n d

 

Bragg’s equation
Missing reflections
Note: The ‘line’ (peak) intensities will be required to determine the motif.
The intensities are determined by structure factor calculations and by including other factors which are specific to the experimental setup
( ) 2 2 2
Cubic crystal
hkl
a
d
h k l

 
Equation connecting ‘d’
to ‘a’(lattice parameter)
Crystal to 2
2 to ‘d’
‘d’to ‘a’

39. Crystal structure determination
Monochromatic X-rays
Panchromatic X-rays
Monochromatic X-rays
Many s (orientations)
Powder specimen
Powder
Method
Single 
Laue
Technique
 Varied by rotation
Rotating Crystal
Method
λ fixed
θ variable


λ fixed
θ rotated


λ variable
θ fixed


 As diffraction occurs only at specific Bragg angles, the chance that a reflection is observed
when a crystal is irradiated with monochromatic X-rays at a particular angle is small (added
to this the diffracted intensity is a small fraction of the beam used for irradiation).
 The probability to get a diffracted beam (with sufficient intensity) is increased by either
varying the wavelength () or having many orientations (rotating the crystal or having
multiple crystallites in many orientations).
 The three methods used to achieve high probability of diffraction are shown below.
Only the powder method (which is commonly used in materials science) will be considered in this text.

40. THE POWDER METHOD

2
2
2
2
sin
)
( 

 l
k
h


2
2
2
2
2
2
sin
4
)
(
a
l
k
h 


)
(
sin
4
2
2
2
2
2
2
l
k
h
a 




2 2 2
hkl Cubic
a
d
h k l

 
2d Sin
 

2
2
2
2
2
2 sin
4
l
k
h
a





Cubic crystal
 In the powder method the specimen has crystallites (or grains) in many orientations (usually
random).
 Monochromatic* X-rays are irradiated on the specimen and the intensity of the diffracted
beams is measured as a function of the diffracted angle.
 The powder method can be used for the following basic purposes: (i) determine the lattice
type (BCC, FCC...), (ii) determine the lattice parameter, (iii) compare with standard
listing** to determine the phase(s) present.
Other uses include the determination of crystallite sizes, micro-strain, phase fractions, etc.
(1) (2)
(2) in (1)


* In reality this is true only to an extent
In this elementary text we shall consider cubic crystals.

41. The ratio of (h2 + k2 + l2) derived from extinction rules (earlier page).
As we shall see soon the ratios of (h2 + k2 + l2) is proportional to Sin2
 which can be used in the determination of the lattice type.
SC ratio 1 2 3 4 5 6 8 …
100
12 + 02 + 02
110
12 + 12 + 02
111
12 + 12 + 02
200
22 + 02 + 02
210
22 + 12 + 02
211
22 + 12 + 12
220
22 + 22 + 02
BCC 2 4 6 8 10 12 14
ratio 1 2 3 4 5 6 7 …
110 200 211 220 310 222 321
FCC ratio
3 4 8 11 12 …
111 200 220 311 222
DC 3 8 11 16 …
111 220 311 400
 Note that we have to consider the ratio of only two lines to distinguish FCC and DC. I.e. if the
ratios are 3:4 then the lattice is FCC.
 But, to distinguish between SC and BCC we have to go to 7 lines!

42.  In the powder sample there are crystallites in different ‘random’ orientations (a polycrystalline sample
too has grains in different orientations)
 The coherent x-ray beam is diffracted by these crystallites at various angles to the incident direction
 All the diffracted beams (called ‘reflections’) from a single plane, but from different crystallites lie on a
cone.
 Depending on the angle there are forward and back reflection cones.
 A diffractometer can record the angle of these reflections along with the intensities of the reflection
 The X-ray source and diffractometer move in arcs of a circle- maintaining the Bragg ‘reflection’
geometry as in the figure (right)
POWDER METHOD
Different cones
for different
reflections
Also called Debye ring
Usually the source is
fixed and the
detector and sample
are rotated

43. How to visualize the occurrence of peaks at various angles
It is ‘somewhat difficult’to actually visualize a random assembly of crystallites giving peaks at various angels in a XRD
scan. The figures below are expected to give a ‘visual feel’for the same. [Hypothetical crystal with a = 4Å is assumed with
=1.54Å. Only planes of the type xx0 (like (100,110)are considered].
Random assemblage of
crystallites in a material
As the scan takes place at increasing
angles, planes with suitable ‘d’,
which diffract are ‘picked out’ from
favourably oriented crystallites
h2 hkl d Sin() 
1 100 4.00 0.19 11.10
2 110 2.83 0.27 15.80
3 111 2.31 0.33 19.48
4 200 2.00 0.39 22.64
5 210 1.79 0.43 25.50
6 211 1.63 0.47 28.13
8 220 1.41 0.54 32.99
9 300 1.33 0.58 35.27
10 310 1.26 0.61 37.50
For convenience the source
may be stationary (and the
sample and detector may
rotate– but the effect is
equivalent)

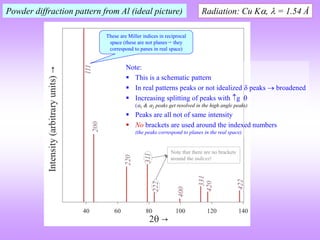
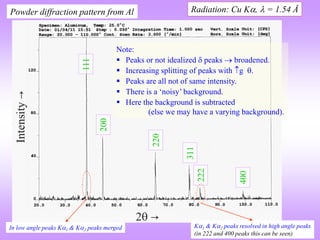
44.  In the power diffraction method a 2 versus intensity (I) plot is obtained from the
diffractometer (and associated instrumentation).
 The ‘intensity’ is the area under the peak in such a plot (NOT the height of the peak).
 The information of importance obtained from such a pattern is the ‘relative intensities*’
and the absolute value of the intensities is of little importance (the longer we irradiate the sample the more will be
the intensity under the peak) (for now).
 I is really diffracted energy (as Intensity is Energy/area/time).
Determination of Crystal Structure from 2 versus Intensity Data in Powder Method
Powder diffraction pattern from Al
Radiation: Cu K,  = 1.54 Å
Increasing 
Increasing ‘d’
 Intensity (I) has units of
[Energy/area/time] → but here
it is plotted as arbitrary units.
 The dwell time at each angle should be
sufficient to get a high “peak to
background” ratio.
2 is the angle of deviation of X-rays.
Usually in degrees ()
This is peak (sometimes called a
line- a hangover from Debye
Scherrer camera usage)
* Relative intensity: Intensity of any peak divided by
the intensity of the ‘strongest’peak.
In a powder XRD pattern the
relative intensities of the peaks
are important.
This diffraction pattern resides in reciprocal/Fourier
space & hence, increasing ‘d’ is to the left
Noisy background.

45. n 2→  Intensity Sin Sin2  ratio
Determination of Crystal Structure (lattice type) from 2 versus Intensity Data
The following table is made from the 2 versus Intensity data (obtained from a XRD experiment on a
powder sample (empty starting table of columns is shown below- completed table shown later).
 A table is prepared as below to tabulate the data and make calculations to find the crystal
structure (restricting ourselves to cubic crystals for the present).
Note (again) that the x-axis is 2, which is the angle of deviation of the X-rays

46. Powder diffraction pattern from Al (ideal picture) Radiation: Cu K,  = 1.54 Å
Note:
 This is a schematic pattern
 In real patterns peaks or not idealized  peaks  broadened
 Increasing splitting of peaks with g 
(1 & 2 peaks get resolved in the high angle peaks)
 Peaks are all not of same intensity
 No brackets are used around the indexed numbers
(the peaks correspond to planes in the real space)
Note that there are no brackets
around the indices!
These are Miller indices in reciprocal
space (these are not planes they
correspond to panes in real space)

47. Powder diffraction pattern from Al
111
200
220
311
222
400
K1 & K2 peaks resolved in high angle peaks
(in 222 and 400 peaks this can be seen)
Radiation: Cu K,  = 1.54 Å
Note:
 Peaks or not idealized  peaks  broadened.
 Increasing splitting of peaks with g .
 Peaks are all not of same intensity.
 There is a ‘noisy’ background.
 Here the background is subtracted
(else we may have a varying background).
In low angle peaks K1 & K2 peaks merged

48. Funda Check How are real diffraction patterns different from the ‘ideal’computed ones?
 We have seen real and ideal diffraction patterns. In ideal patterns the peaks are ‘’ functions.
 Real diffraction patterns are different from ideal ones in the following ways:
 Peaks are broadened
Could be due to instrumental, residual ‘non-uniform’strain (microstrain), grain size etc. broadening.
 Peaks could be shifted from their ideal positions
Could be due to uniform strain→ macrostrain.
 Relative intensities of the peaks could be altered
Could be due to texture in the sample.
 Presence of diffuse intensity* between the Bragg peaks
Diffuse intensity can arise due to atomic disorder and thermal vibrations.
Instrumental broadening
Crystal defects (‘bent’planes), etc.
Peak
Broadening
Small crystallite size
Note peak splitting has not been
included here as this comes from
‘symmetry lowering’(i.e. crystal with
lower symmetry)
Including those coming from strain
fields associated with these defects
Click here to know more
Macro-strain will lead to peak shift, while
micro-strain (e.g. due to dislocations will lead
to peak broadening)
* Diffuse intensity.
 In the powder diffraction pattern, usually there exists low intensity ‘noise’ between the Bragg
peaks. This has origins which do not relate to the sample.
 In addition to this ‘experimental noise’, diffuse intensity (typically much lower in magnitude)
can arise due to defects in the sample like atomic disorder and thermal vibrations.

49. What is the maximum value of  possible (experimentally)?
Funda Check Ans: 90
 At  = 90 the ‘reflected ray’ is opposite in
direction to the incident ray.
 Beyond this angle, it is as if the source and
detector positions are switched.
  2max is 180.

50. Funda Check Which crystal defects give rise to Bragg peak broadening and which ones result
in diffuse scattering?
 The intensity in a diffraction pattern resides under the Bragg peaks and between the Bragg peaks. The
intensity between the Bragg peaks is called diffuse scattering and is of much lower magnitude than the
Bragg peaks. As we have noted, the Bragg peak is typically not a ‘’ function, but is broadened due to
various reasons.
 Some crystal defects give rise to only broadening and other lead to diffuse scattering in addition to
broadening.
 Thermal vibration of atoms give rise to the following effects: (i) decrease in peak intensity, (ii) increase
in diffuse scattering between the peaks, (iii) no peak broadening & (iv) peak displacement due to
thermal expansion (increase in lattice parameter).
 Point defects will lead to increased diffuse scattering. Point defects include the formation of dilute
alloys and the presence of vacancies. Vacancies will lead to slight peak shift due to a decrease in the
lattice parameter.
 Defects like dislocations (& stacking faults) has the following effects: (i) peak broadening, (ii) no
decrease in the intensity, (iii) increase in diffuse scattering.
 Decrease in crystallite size leads to: (i) peak broadening, (ii) decrease in the intensity.
 Formation of a concentrated disordered solid solution leads to: (i) peak broadening, (ii) increase in
diffuse scattering. The intensity of the peaks will depend on the average atomic scattering factor. The
peak position will depend on the average lattice parameter.

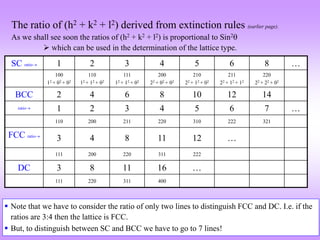
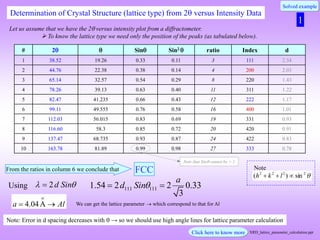
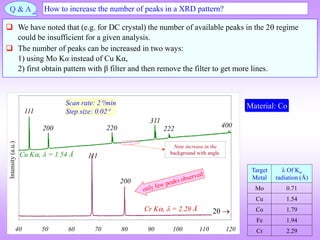
51. Funda Check What will determine how many peaks I will get?
 1)   smaller the wavelength of the X-rays, more will be the number of peaks possible.
 From Bragg’s equation: [=2dSin], (Sin)max will correspond to dmin. (Sin)max=1.
Hence, dmin=/2. Hence, if  is small then planes with smaller d spacing (i.e. those which
occur at higher 2 values) will also show up in a XRD patter (powder pattern). Given that
experimentally  cannot be greater than 90.
 2) Lattice type  in SC we will get more peaks as compared to (say) FCC/DC. Other things being
equal.
 3) Lower the symmetry of the crystal, more the number of peaks (e.g., in tetragonal crystal
the 100 peak will lie at a different 2 as compared to the 001 peak).
2dSin
 

  min
max
2d
Sin


 min
2
d



52. # 2  Sin Sin2  ratio Index d
1 38.52 19.26 0.33 0.11 3 111 2.34
2 44.76 22.38 0.38 0.14 4 200 2.03
3 65.14 32.57 0.54 0.29 8 220 1.43
4 78.26 39.13 0.63 0.40 11 311 1.22
5 82.47 41.235 0.66 0.43 12 222 1.17
6 99.11 49.555 0.76 0.58 16 400 1.01
7 112.03 56.015 0.83 0.69 19 331 0.93
8 116.60 58.3 0.85 0.72 20 420 0.91
9 137.47 68.735 0.93 0.87 24 422 0.83
10 163.78 81.89 0.99 0.98 27 333 0.78
Determination of Crystal Structure (lattice type) from 2 versus Intensity Data
From the ratios in column 6 we conclude that FCC
Let us assume that we have the 2 versus intensity plot from a diffractometer.
 To know the lattice type we need only the position of the peaks (as tabulated below).
Solved example
2d Sin
 
 111 111
1.54 2 2 0.33
3
a
d Sin
 
o
4.04A
a Al
 
Using
We can get the lattice parameter  which correspond to that for Al
1
Note: Error in d spacing decreases with  → so we should use high angle lines for lattice parameter calculation
Click here to know more
Note that Sin cannot be > 1
XRD_lattice_parameter_calculation.ppt

2
2
2
2
sin
)
( 

 l
k
h
Note

53. 2→  Sin Sin2 
Ratios
of Sin2
Dividing Sin2 by
0.134/3 = 0.044667
Whole
number
ratios
Index
1 21.5 0.366 0.134 1 3 111
2 25 0.422 0.178 1.33 3.99 4 200
3 37 0.60 0.362 2.70 8.10 8 220
4 45 0.707 0.500 3.73 11.19 11 311
5 47 0.731 0.535 4 11.98 12 222
6 58 0.848 0.719 5.37 16.10 16 400
7 68 0.927 0.859 6.41 19.23 19 331
 FCC lattice
Another example
Given the positions of the Bragg peaks we find the lattice type
Solved example
2

54. More Solved
Examples on XRD Click here
Comparison of diffraction patterns of SC, BCC & B2 structures
Click here

55. Aluminium  = 1.54 Å  = 3 Å  = 0.1 Å
hkl d Sin()  2 Sin()  2 Sin()  2
111 2.34 0.33 19.26 38.52 0.64 39.87 79.74 0.02 1.22 2.45
200 2.03 0.38 22.38 44.76 0.74 47.64 95.28 0.02 1.41 2.82
220 1.43 0.54 32.57 65.14 1.05 - - 0.03 2.00 4.01
311 1.22 0.63 39.13 78.26 1.23 - - 0.04 2.35 4.70
222 1.17 0.66 41.24 82.47 1.28 - - 0.04 2.45 4.90
400 1.01 0.76 49.56 99.11 1.49 - - 0.05 2.84 5.68
331 0.93 0.83 56.02 112.03 1.61 - - 0.05 3.08 6.16
420 0.91 0.85 58.30 116.60 1.65 - - 0.05 3.15 6.30
422 0.83 0.93 68.74 137.47 1.81 - - 0.06 3.45 6.91
333 0.78 0.99 81.89 163.78 1.92 - - 0.06 3.68 7.35
Funda Check What happens when we increase or decrease ?
We had pointed out that  ~ a is preferred for diffraction. Let us see what happens if we ‘drastically’
increase or decrease .
(This is only a thought experiment as obtaining monochormatic x-rays with any arbitrary wavelength and
good intensity is ‘difficult’!!)
If we ~double  → we get too
few peaks
If we make  small→
all the peaks get
crowded to small
angles
With CuK  = 1.54 Å
And the detector may not be able to resolve
these peaks if they come too close!

56.  Most often materials scientists use powder patterns to determine the phases present in a
sample. In this ‘finger printing’ technique, the data obtained (I versus 2) is compared with
standard tables (e.g. the ICPD or the JCPDS data listing) to know the phases present.
 When only a single phase is present, the task is reasonably simple. However, in the presence
of multiple phases, the process can be tricky.
 For a perfect match with the data tables, both the relative intensity and the peak positions
(2) have to match ‘perfectly’. However, w.r.t data from real samples, the relative intensity
will be typically different from that in the tables. This is usually due to crystallographic
texture (i.e. the lack of random orientations of crystallites and the presence of ‘preferred
orientation’). Crystallographic texture typically arises from metal deformation processes like rolling, extrusion, etc.
The lack of sufficient number of crystallites (in random orientations) can also lead to a ‘mismatch’
between the observed relative intensity and that in the ICDD tables.
 The shift of Bragg peaks from that in the tables (ICDD) can arise due to presence of
impurities in the sample, which form a solid solution (this is assuming that there is no ‘offset error’ in the
instrumentation).
 The typical process of matching the data obtained with the database (finger printing) starts
with knowing the elements present in the sample (say an alloy) and having the list of phases
that can form in the system (the list of phases can be obtained from a phase diagram or a crystallography database (like the
Pearson’s crystallographic database)).
 The number of phases to be dealt with can be reduced by knowing the processing
conditions and its implication on the kind of phases which are expected to form.
Determination of the phases present using the powder diffraction data

57.  It should be noted that, even if a perfect match for all the peaks cannot be made, the 2
position of ‘most’ of the high intensity peaks should match.
 A definitive identification cannot be made by just matching a few peaks.
 The process (of identification of phases) gets very complicated when: (i) multiple phases
are present and/or (ii) there exist one or more similar phases (in terms of their XRD pattern)
and one (or more) of them is (are) present in your sample.
 In any case XRD cannot be used to rule the presence of phases, as the sensitivity of the
technique for phases present in less than 1% (say by vol.%) is not good. Powder XRD data
is best used in conjunction with other characterization techniques like SEM and TEM.
 Typically, powder data is not used for the identification of previously unknown phases. This
is best done with single crystal data. Techniques like Rietveld refinement can be used for
the determination of unknown crystal structures using powder data (especially if the option of single
crystal experiment is ruled out).
 Rietveld refinement can also be used to obtain the phase fractions (i.e. the fractions of
various phases present in the sample). Software like ‘Fullprof’ can be used for this purpose.

58. Bravais lattice determination
Lattice parameter determination
Determination of solvus line in phase diagrams
Long range order
Applications of XRD
Crystallite size and Strain
Determine if the material is amorphous or crystalline
We have already seen these applications
Click here to know more
Next slide And More….
 XRD is a versatile tool, which can be used to obtain many kinds of information about the
sample. A few are listed in the figure below.
 Often there are competing tools which can give a better result. E.g. TEM is a better tool to
obtain the strain distribution around a coherent precipitate as compared to XRD. However,
often the advantage of XRD is the ‘spatially averaged’ data and the ‘large scale sampling’
(i.e. sampling can be from a large volume as compared to TEM).
Other uses of XRD

59. Diffraction angle (2) →
Intensity
→
90 180
0
Crystal
90 180
0
Diffraction angle (2) →
Intensity
→
Liquid / Amorphous solid
90 180
0
Diffraction angle (2) →
Intensity
→
Monoatomic gas
Schematic of difference between
the diffraction patterns of various phases
Sharp peaks
Diffuse Peak
No peak
Schematics
Determine if the material is amorphous or crystalline
Continued…

60. 20 30 40 50 60 70
2θ (  ) 
Intensity
(a.u.)
Actual diffraction pattern
from an amorphous solid
 A amorphous solid, which shows glass transition in a Differential Scanning Calorimetry
(DSC) plot is also called a glass. In ‘general usage’a glass may be considered equivalent to a
amorphous solid (at least loosely in the structural sense).
 In the XRD pattern obtained from a glass, the sharp peaks (which are present in the XRD
pattern from crystals) are missing. Only a broad diffuse peak survives→ the peak corresponds to
the average spacing between atoms which the diffraction experiment ‘picks out’
Amorphous solid
XRD pattern showing the formation of amorphous
structure in the suction cast (Cu64Zr36)96Al4 alloy.

61. Funda Check  What is the minimum spacing between planes possible in a crystal?
 How many diffraction peaks can we get from a powder pattern?
2 2 2
Cubic crystal
hkl
a
d
h k l

 
Let us consider a cubic crystal (without loss in generality)
As h,k, l increases, ‘d’ decreases  we could have planes with infinitesimal spacing
10
1
a
d a
 
11
2
a
d 
13
10
a
d 
12
5
a
d 
34
5
25
a a
d  
With increasing indices the
interplanar spacing decreases
The number of peaks we obtain in a powder
diffraction pattern depends on the wavelength
of x-ray we are using. Planes with ‘d’ < /2 are
not captured in the diffraction pattern.
These peaks with small ‘d’ occur at high angles
in diffraction pattern.

62. Q & A How to increase the number of peaks in a XRD pattern?
 We have noted that (e.g. for DC crystal) the number of available peaks in the 2 regime
could be insufficient for a given analysis.
 The number of peaks can be increased in two ways:
1) using Mo Kα instead of Cu Kα,
2) first obtain pattern with β filter and then remove the filter to get more lines.
Target
Metal
 Of K
radiation (Å)
Mo 0.71
Cu 1.54
Co 1.79
Fe 1.94
Cr 2.29
40 50 60 70 80 90 100 110 120
2θ 
Intensity
(a.u.)
Scan rate: 2/min
Step size: 0.02
Cu K,  = 1.54 Å
Note increase in the
background with angle.
Cr K,  = 2.29 Å
111
Material: Co
200 220 222
311
400
111
200

63. Q & A In early parts of the chapter, we had noted that we have many sources of nearly
monochromatic X-rays are available. Why are so many radiation sources needed?
 There are two main reasons why we need some options at our disposal.
 1) Some sources ‘fluoresce’ with in conjunction with some elements in the material (e.g. Co
fluoresces with Cu K). This inelastic process gives rise to an increased background and
hence a lower signal to background ratio. In the case of Co in the sample, Cr K radiation can
be used.
 2) Smaller wavelengths of radiation give rise to more peaks in a powder XRD pattern. Cu K
gives more peaks as compared to Cr K radiation. (The point we saw previously).
40 50 60 70 80 90 100 110 120
2θ 
Intensity
(a.u.)
Scan rate: 2/min
Step size: 0.02
Cu K,  = 1.54 Å
Note increase in the background with
angle due to fluorescence (Co with
Cu K radiation)
Cr K,  = 2.29 Å
111
Material: Co
200 220 222
311
400
111
200
No fluorescence (Co with Cr K)
Also note: low
peak to
background ratio.

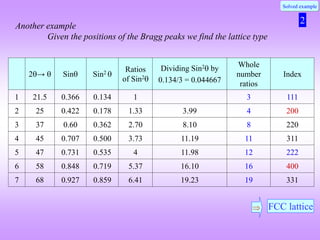
64. What is the natural variable for plotting powder diffraction data?
Funda Check
 The usual plot is between Intensity and 2. It is not  but 2; as this is the angle of deviation
of the incident beam. Could it have not been ?
 Usually, the variation of atomic scattering factor (f) is plotted with Sin/.
1
2


hkl
hkl
d
Sin

 
 
 
Braggs’equation can be rewritten as: Hence, Sin/ can also serve as a
‘natural variable’for the abscissa
[Units: /Å1].
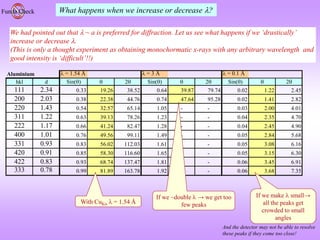
Sample: Cu
0.2 0.25 0.3 0.35 0.4 0.45
Sin()/
Intensity
Cu Ka
Cr Ka
Number of lines are limited due to longer wavelength of Cr K
XRD powder pattern taken from a Cu
sample with two sources of radiation:
CuK and CrK .
As expected the peaks coincide if plotted
with Sin/ as the abscissa (as now this is
a measure of dhkl .
Coinciding peaks
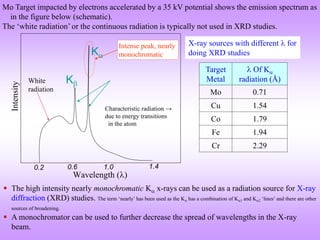
Target Metal
 Of K
radiation (Å)
 Cu K 1.54
 Cr K 2.29
111
200

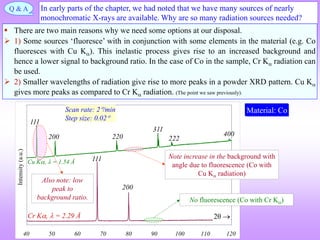
65. Q & A What are the ways can we represent dimensions and vectors in a diffraction pattern?
 The diffraction pattern resides in the reciprocal space or Fourier space. Reciprocal lattice
points are decorated by intensities to create a reciprocal crystal. We would like to measure
‘distances’ and draw vectors in reciprocal space. Here we consider ways of doing this.
 The units in reciprocal space is [m1]. Usually, expressed as Å1 or nm1.
 The reciprocal space vectors are vectors in reciprocal space (more details in the link below);
usually marked with a star (*).
 There are other ways of representing dimensions/vectors in reciprocal space (as below).
*
b2

*
b1

3
*
b
2
| |
k



4
| | 2 ( ) ( )
G q k Sin Sin

 

  
2 ( )
n d Sin
 

2 ( )
n
d Sin
 

1 ( )
2
n
Sin
d




  
 

66. Solved
Example
During a powder diffraction experiment, at what  does the first peak from BCC Fe
and FCC Fe occur?
 First a point regarding the assumption. The ‘radius of the atom’ (Fe in the current case)
depends on the crystal structure and the local electronic environment and hence .
 Also, the answer to the question: “What is the radius of an atom?” is a tricky one (even for a
free atom, let alone in a metallic alloy).
 The first peak for BCC is from the (110) planes, while for FCC it is from the (110) planes.
Assume that the radius of the Fe atom is the same in both the structures.
Fe Fe
BCC FCC
r r

2


n k
Sin
d d
 
3 4 Fe
a r

BCC
2 4 Fe
a r

110
2
a
d 
111
3
a
d 
FCC
110
(110)
6
4
 BCC
Fe
k
Sin k
d r
 
111
(111)
6
4
 FCC
Fe
k
Sin k
d r
 
This implies that the position of the first Bragg peak at the same  location (though in reality it will shift a
little due to the change in the value of ‘r’between the FCC and BCC structures).

67. Structure Factor (F)
Multiplicity factor (p)
Polarization factor
Lorentz factor
Relative Intensity of diffraction lines in a powder pattern
Absorption factor
Temperature factor
Scattering from UC (Atomic Scattering Factor is included in this term)
Number of equivalent scattering planes
Effect of wave polarization
Combination of 3
geometric factors
Specimen absorption
Thermal diffuse scattering
  














 2
1
2
1
Sin
Cos
Sin
factor
Lorentz
 
 

2
1 2
Cos
IP 

structure_factor_calculations.ppt
Details are in the next few slides a beginner may skip these
The Lorentz and polarization factors both depend on  (geometry) and are usually combined into the Lorentz-
polarization factor

68. Detailed calculation of the intensity of a Bragg peak in a powder pattern
The integrated intensity per unit length of the diffraction line (J/s.m) in the powder
diffraction patterns obtained from a single phase sample can be written as [1]:
2
3 4
0 0
1 2 2
2
32 4
net
I A e
I I I I
r m
 
 
 
 
   
 
 
 
 
 
(1)
where, A is the cross-sectional area of the incident beam (m2
), λ is the wavelength of the
incident radiation (m), r is the radius of the diffractometer circle (0.185 m under the current
experimental conditions), μ0 is the permeability constant (4π10−7
m.kg/C2
), m is the mass of
the electron (kg), e is the charge on the electron (C) and I0 (= Bi(VVK)n
) is intensity of the
incident beam (J/m2
.s). The term I1 can be written as:
 
1
n
3 3
0 K
I =Constants(I )(λ )=Constants Bi V-V (λ )
 
  (2)
where, B is a proportionality constant, i and V are the applied current and voltage respectively,
VK is the excitation voltage for the K-shell electron and n is an exponent.
[1] Suryanarayana C and Norton MG. 1998 X-Ray Diffraction A Practical Approach. New York, N.Y: Plenum Press.

69. The value of VK can be calculated using the relation below.
K
K
h c
V
e 

 (3)
where, h is the Planck's constant, c is the velocity of light, e is the charge of electron and λKα is
the wavelength of Kα line, which depends on the type of radiation used. The values of  and
VK for three radiations (Cu Kα, Cr Kα and Mo Kα) are listed in the table. This implies that, in
order to make a comparison of the intensities observed in an XRD experiments, the
wavelength of the radiation and the excitation voltage have to be taken into account.
The factors to be considered in the determination of I2 are the following.
(1) Atomic scattering factor (f).
(2) Mass absorption coefficient (  ).
(3) Temperature factor (
2 T
M
e
).
(4) Lorentz-Polarization (LP) factor.
(5) Multiplicity factor (p).
(6) Unit cell volume ( UC
v
).

70. The intensity observed in a powder diffraction pattern due to a combination of previously
considered factors is as follows.
     
 
2 2
2
2
2 2
2 2
1
( ) ( )
1 1 cos 2 1
2 sin cos
T
UC
S A T SAT
M
alloy UC
I Structure Absorption Temperature Multiplicity LP
v
I I I three terms I three terms
F e p
v

  



 

 
     
 
  


 
 
 
  
  



   
   
   
   
(4)
where, F is the structure factor, μ is the linear absorption coefficient, p is the multiplicity
factor, MT
is the Debye-Waller Factor and UC
v is the unit cell volume. The labels in the square
brackets correspond to the various factors.
Incident
Radiation
Wavelength,
 (Ǻ)
Excitation
Voltage, VK (kV)
Cu Kα 1.54 8.04
Cr Kα 2.29 5.41
Mo Kα 0.71 17.46

71. End

73. Diffuse peak from
Cu-Zr-Ni-Al-Si
Metallic glass
(XRD patterns) courtesy: Dr. Kallol Mondal, MSE, IITK