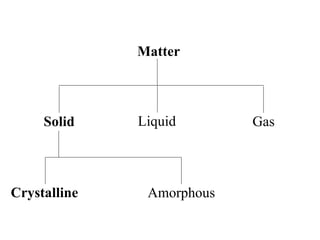
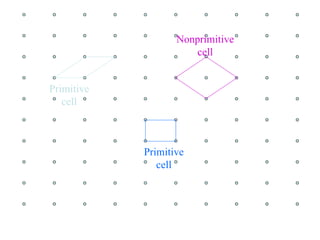
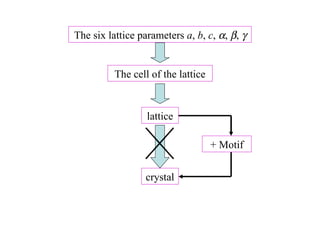
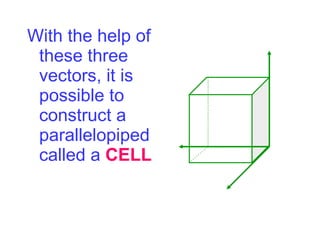
Crystals have basic building blocks called unit cells that are arranged in a periodic pattern described by a lattice. The unit cells contain motif groups of atoms associated with each lattice point. There are 14 possible types of space lattices belonging to 7 crystal systems characterized by distinct unit cell shapes and symmetries. The crystal structure is defined by the space lattice and the motif or basis group of atoms.

1. Crystallography

2. In 1669 Nicolaus Steno found angles between adjacent prism faces of quartz crystal (interfacial angle), to be 120 °. In 1780 Carangeot invented the goniometer, a protactor like device used to measure interfacial angles on crystals. Law of “constancy of interfacial angels”: angles between equivalent faces of crystals of the same mineral are always the same.The law acknowledges that the size and shape of the crystal may vary.

3. In 1784 Rene’Hauy hypothesized the existence of basic building blocks of crystals called integral molecules and argued that large crystals formed when many integral molecules bonded together.

4. Old view Crystals are made of small building blocks The blocks stack together in a regular way, creating the whole crystal. Each block contains a small number of atoms All building blocks have the same atomic composition The building block has shape and symmetry of the entire crystal. We now accept that: Crystals have basic building blocks called unit cells The unit cells are arranged in a pattern described by points in a lattice. The relative proportions of elements in a unit cell are given by the chemical formula of a mineral. Crystals belong to one of the seven crystal systems. Unit cells of distinct shape and symmetry characterize each crystal system. Total crystal symmetry depends on Unit cell symmetry and lattice symmetry.

5. Crystal Geometry Crystals Lattice Lattice points, lattice translations Cell--Primitive & non primitive Lattice parameters Crystal=lattice+motif

6. Matter Crystalline Amorphous Solid Liquid Gas

7. Crystal?

8. A 3D translationally periodic arrangement of atoms in space is called a crystal.

9. A two-dimensional periodic pattern by a Dutch artist M.C. Escher

10. Lattice?

11. A 3D translationally periodic arrangement of points in space is called a lattice.

12. A 3D translationally periodic arrangement of atoms Crystal A 3D translationally periodic arrangement of points Lattice

13. What is the relation between the two? Crystal = Lattice + Motif Motif or basis: an atom or a group of atoms associated with each lattice point

14. Crystal=lattice+basis Lattice: the underlying periodicity of the crystal, Basis: atom or group of atoms associated with each lattice points Lattice: how to repeat Motif: what to repeat

15. + Love Pattern Love Lattice + Heart =

16. Space Lattice A discrete array of points in 3-d space such that every point has identical surroundings

17. Lattice Finite or infinite?

18. Primitive cell Primitive cell Nonprimitive cell

19. Cells A cell is a finite representation of the infinite lattice A cell is a parallelogram (2D) or a parallelopiped (3D) with lattice points at their corners. If the lattice points are only at the corners, the cell is primitive. If there are lattice points in the cell other than the corners, the cell is nonprimitive.

20. Lattice Parameters Lengths of the three sides of the parallelopiped : a, b and c. The three angles between the sides:  ,  , 

21. Convention a parallel to x -axis b parallel to y -axis c parallel to z -axis Angle between y and z Angle between z and x  Angle between x and y

22. The six lattice parameters a , b , c ,  ,  ,  The cell of the lattice lattice crystal + Motif

24. In order to define translations in 3-d space, we need 3 non-coplanar vectors Conventionally, the fundamental translation vector is taken from one lattice point to the next in the chosen direction

25. With the help of these three vectors, it is possible to construct a parallelopiped called a CELL

26. The smallest cell with lattice points at its eight corners has effectively only one lattice point in the volume of the cell. Such a cell is called PRIMITIVE CELL

27. Bravais Space Lattices Conventionally, the finite representation of space lattices is done using unit cells which show maximum possible symmetries with the smallest size. Symmetries: 1.Translation 2. Rotation 3. Reflection

28. Considering Maximum Symmetry, and Minimum Size Bravais concluded that there are only 14 possible Space Lattices (or Unit Cells to represent them). These belong to 7 Crystal Classes

29. Arrangement of lattice points in the unit cell 8 Corners (P) 8 Corners and 1 body centre (I) 8 Corners and 6 face centres (F) 8 corners and 2 centres of opposite faces (A/B/C) Effective number of l.p.

30. Cubic Crystals Simple Cubic (P) Body Centred Cubic (I) – BCC Face Centred Cubic (F) - FCC

31. Tetragonal Crystals Simple Tetragonal Body Centred Tetragonal

32. Orthorhombic Crystals Simple Orthorhombic Body Centred Orthorhombic Face Centred Orthorhombic End Centred Orthorhombic

33. Hexagonal Crystals Simple Hexagonal or most commonly HEXAGONAL Rhombohedral Crystals Rhombohedral (simple)

34. Monoclinic Crystals Simple Monoclinic End Centred Monoclinic (A/B) Triclinic Crystals Triclinic (simple)

35. Crystal Structure Space Lattice + Basis (or Motif) Basis consists of a group of atoms located at every lattice point in an identical fashion To define it, we need to specify Number of atoms and their kind Internuclear spacings Orientation in space

36. Atoms are assumed to be hard spheres