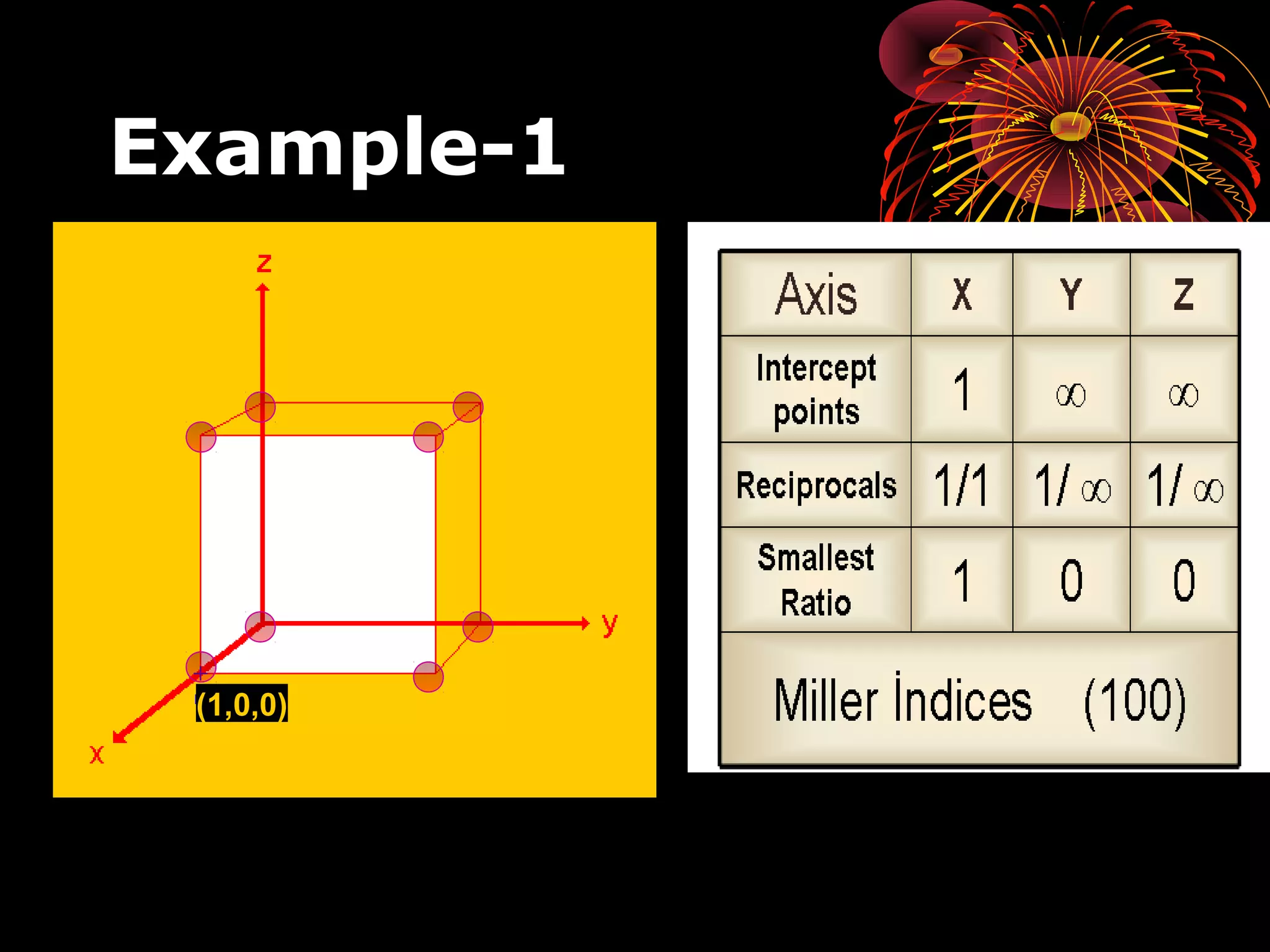
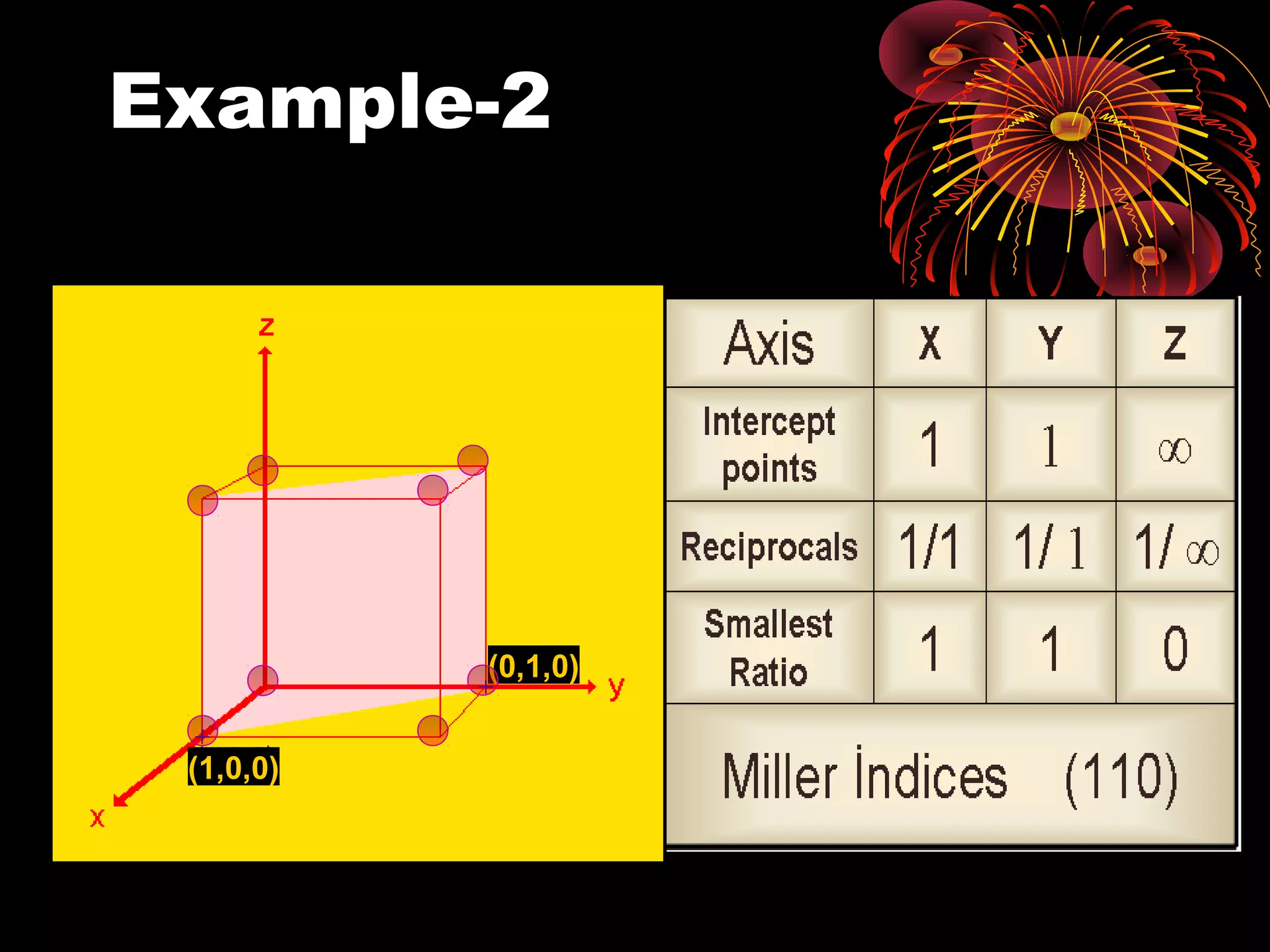
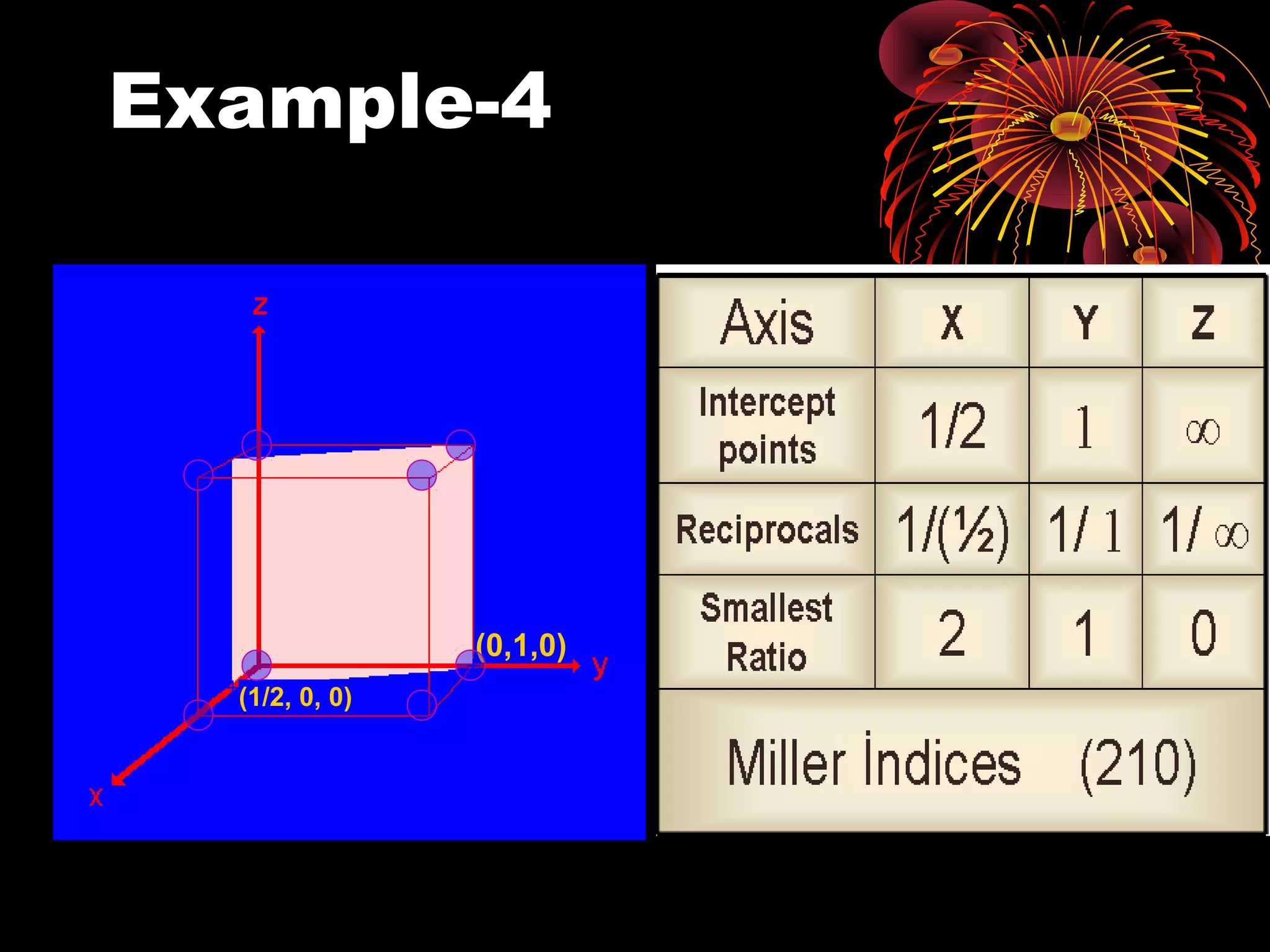
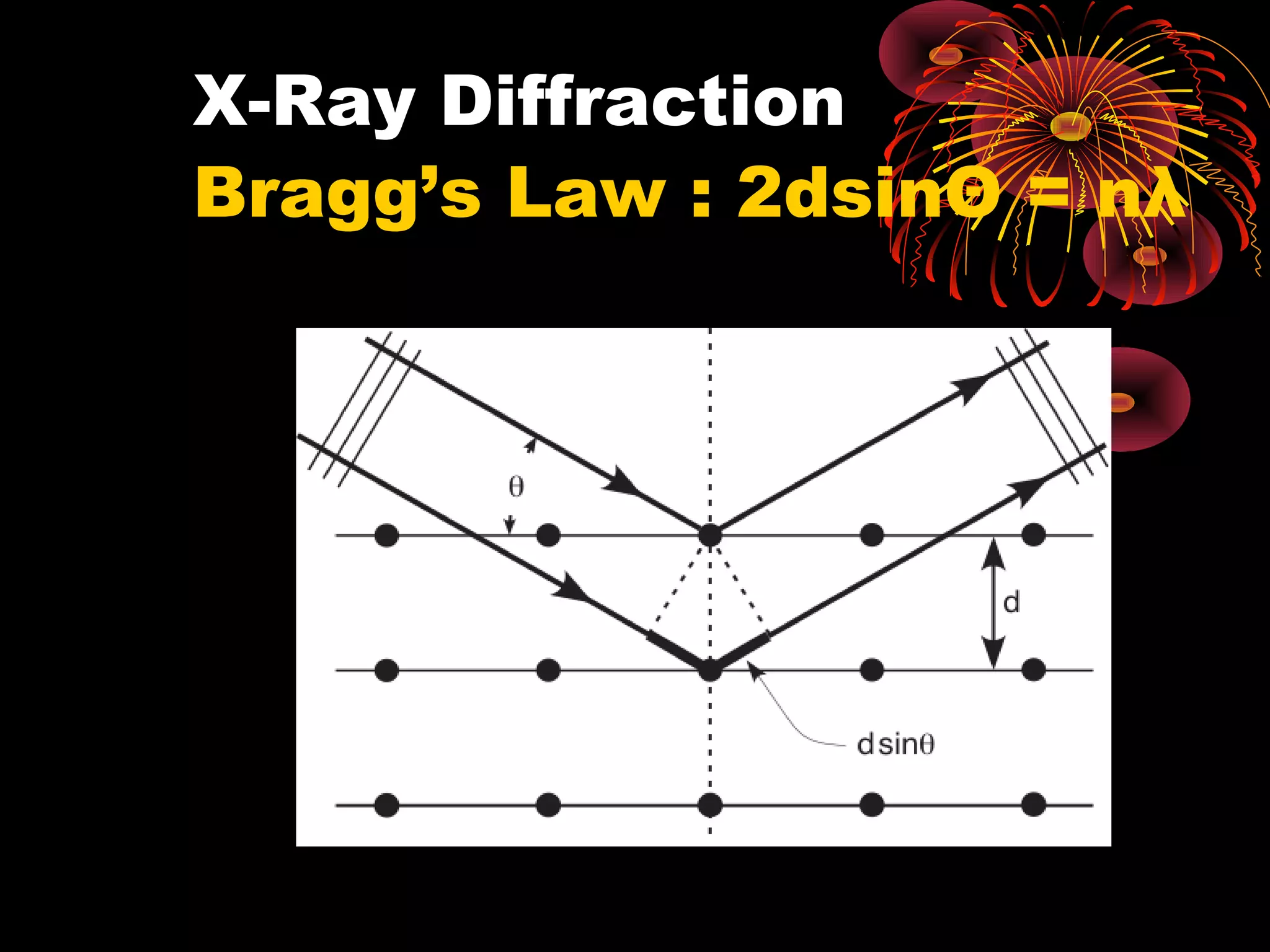
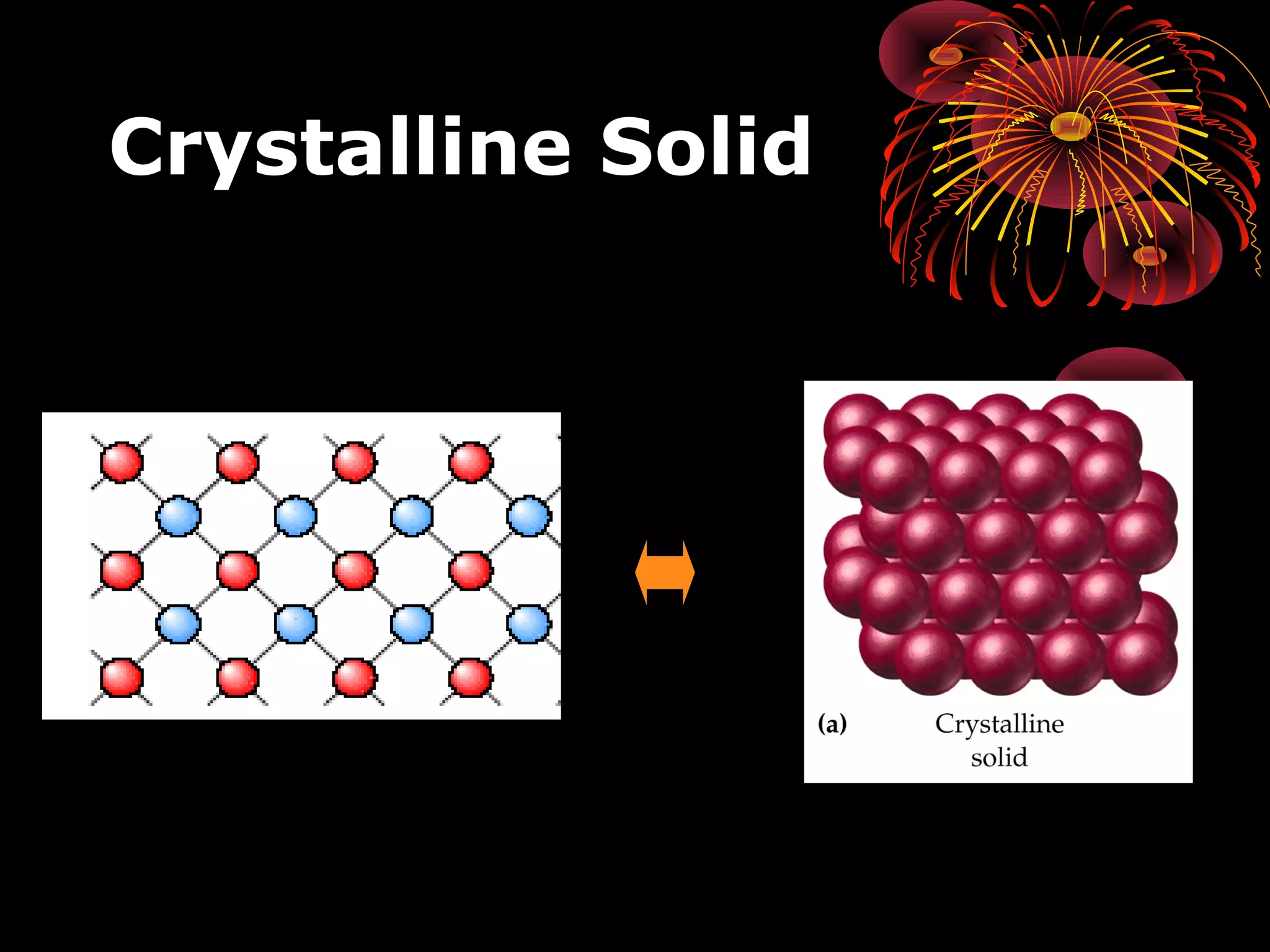
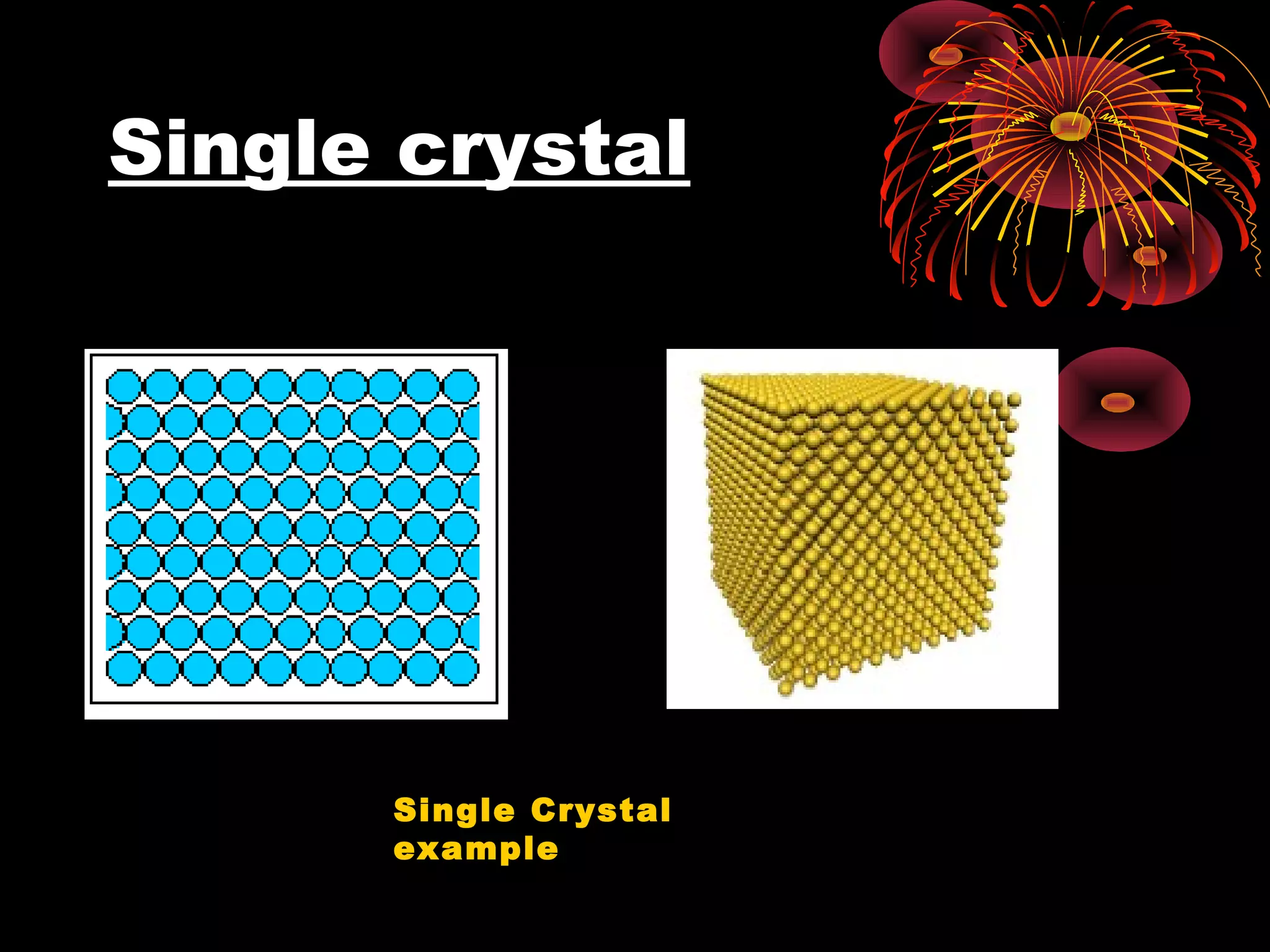
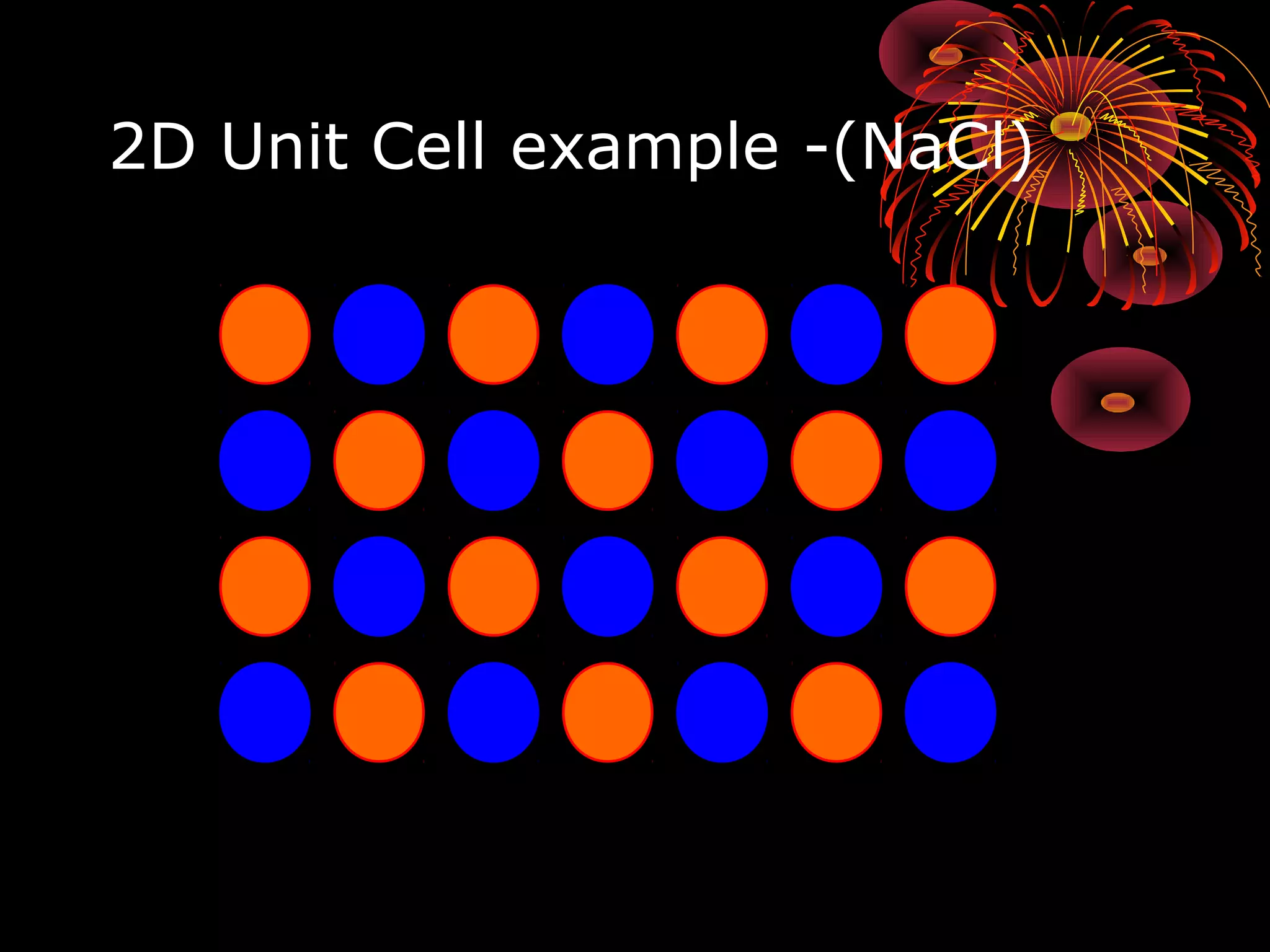
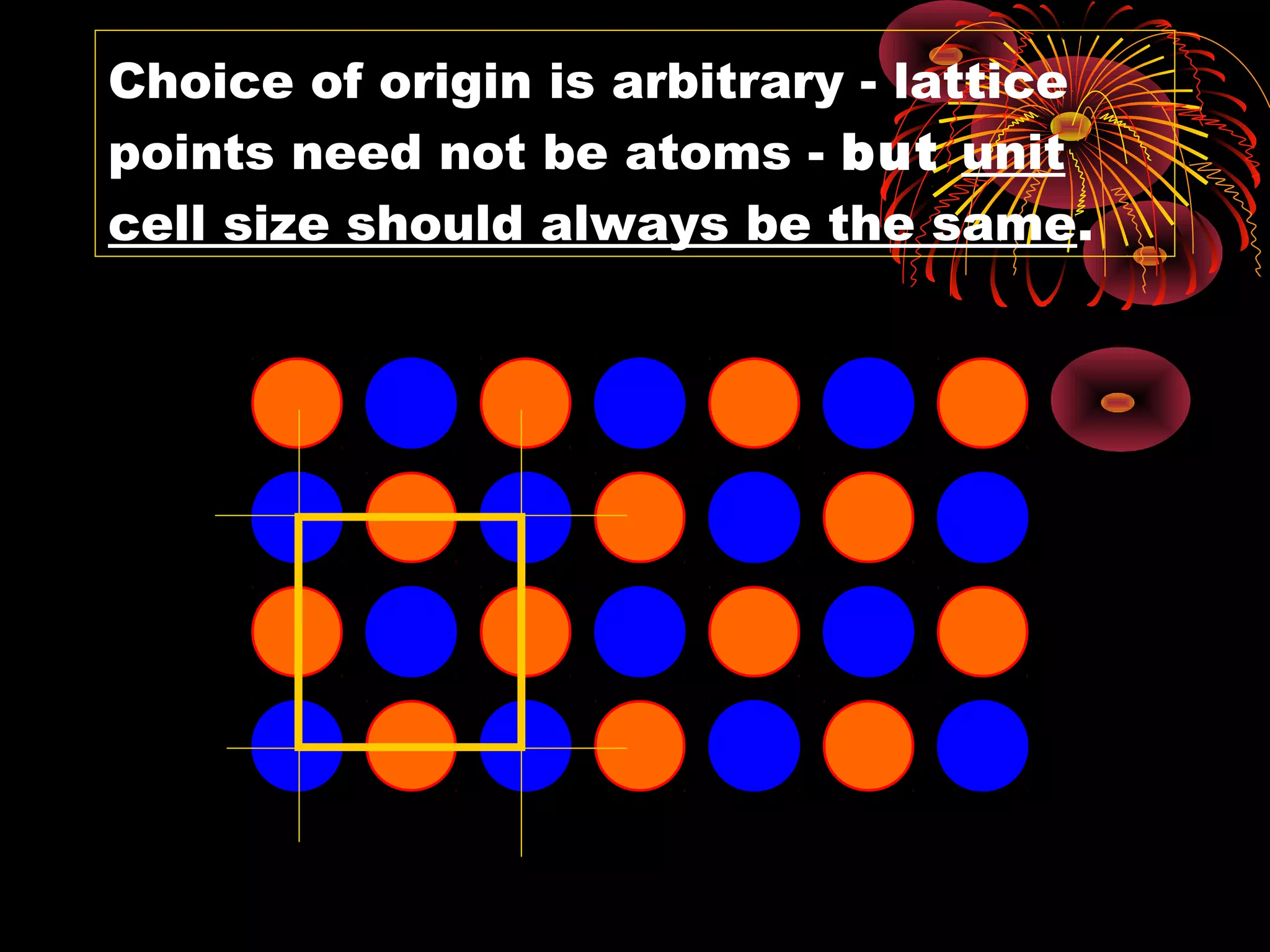
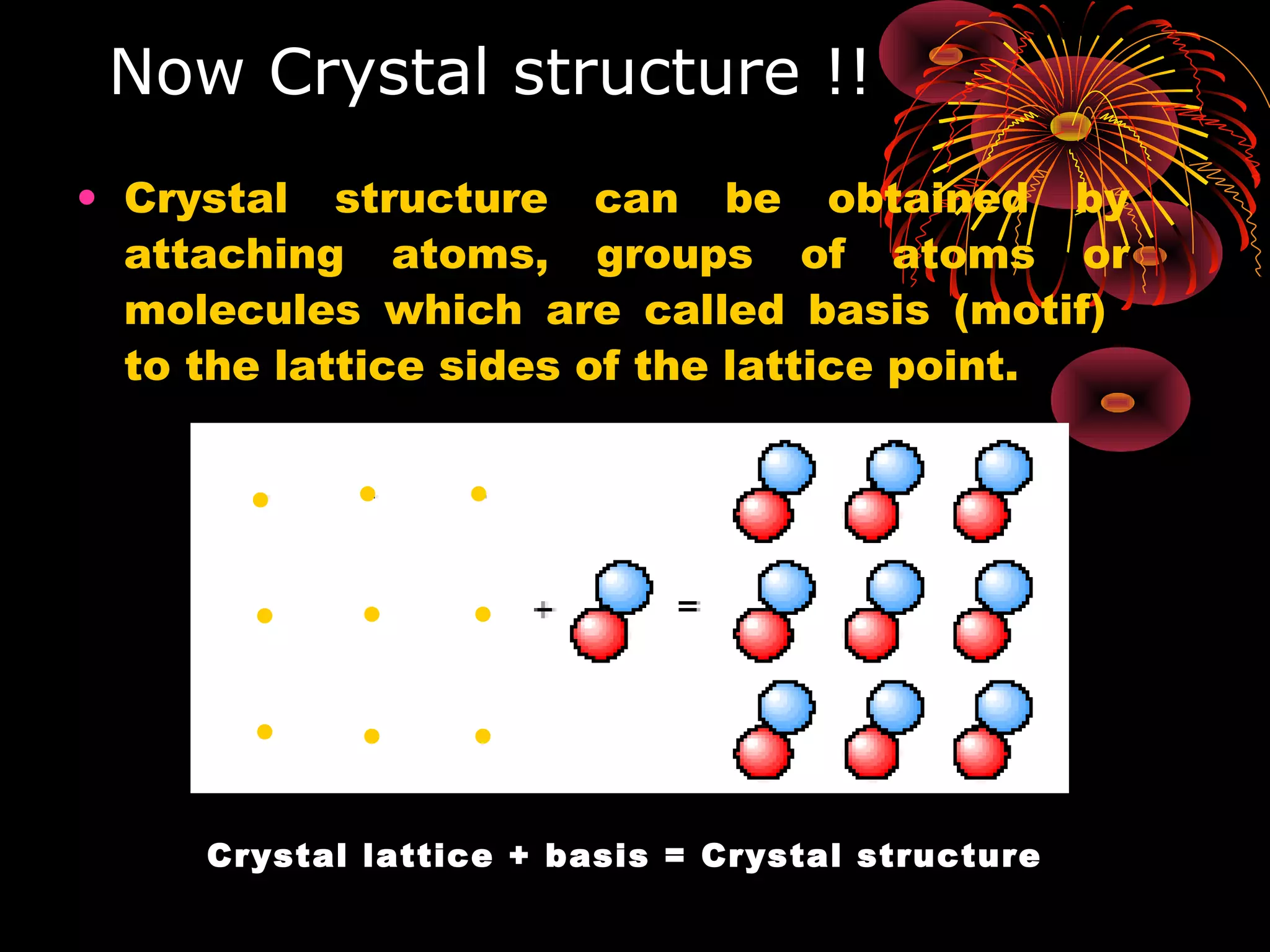
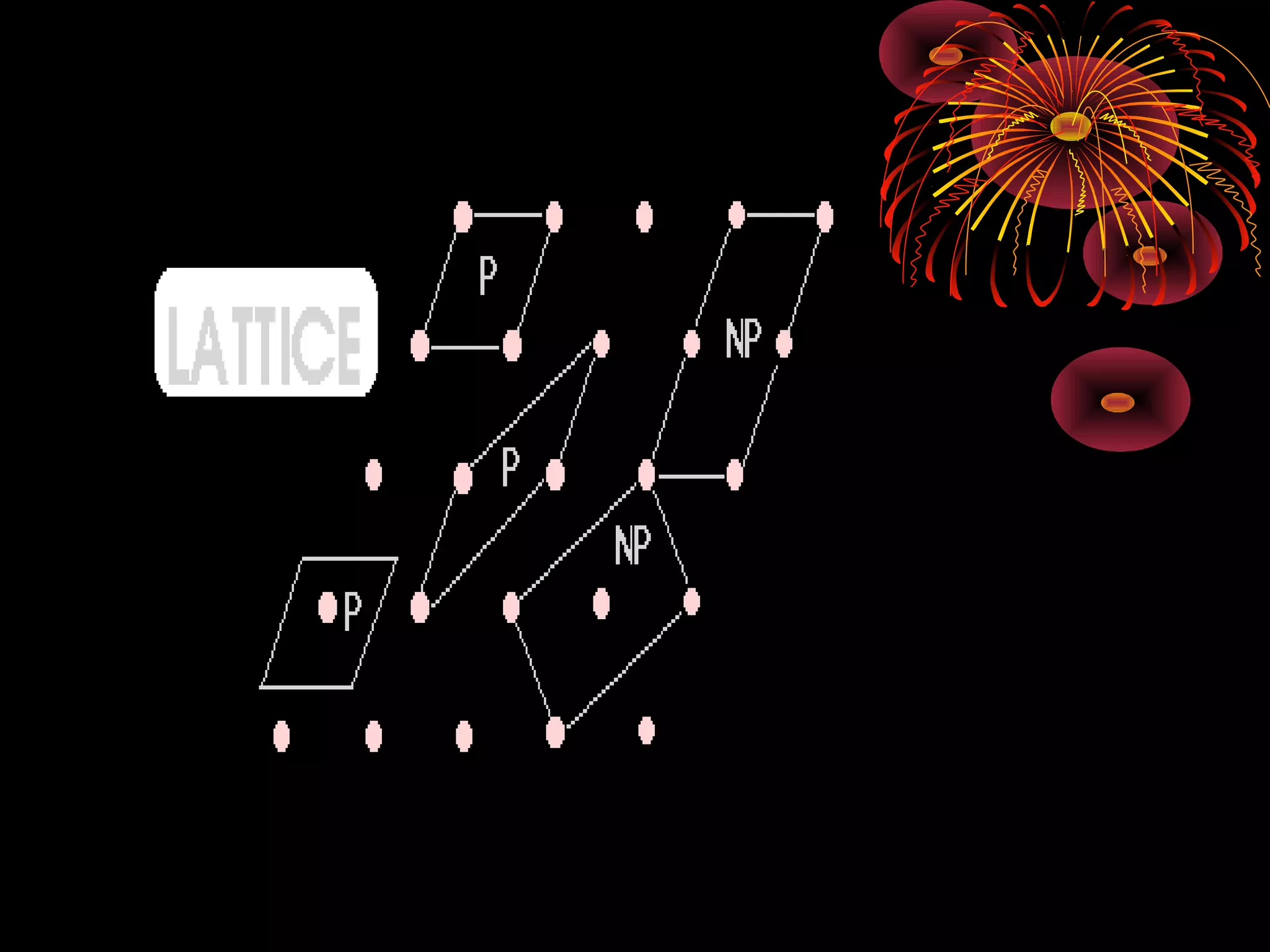
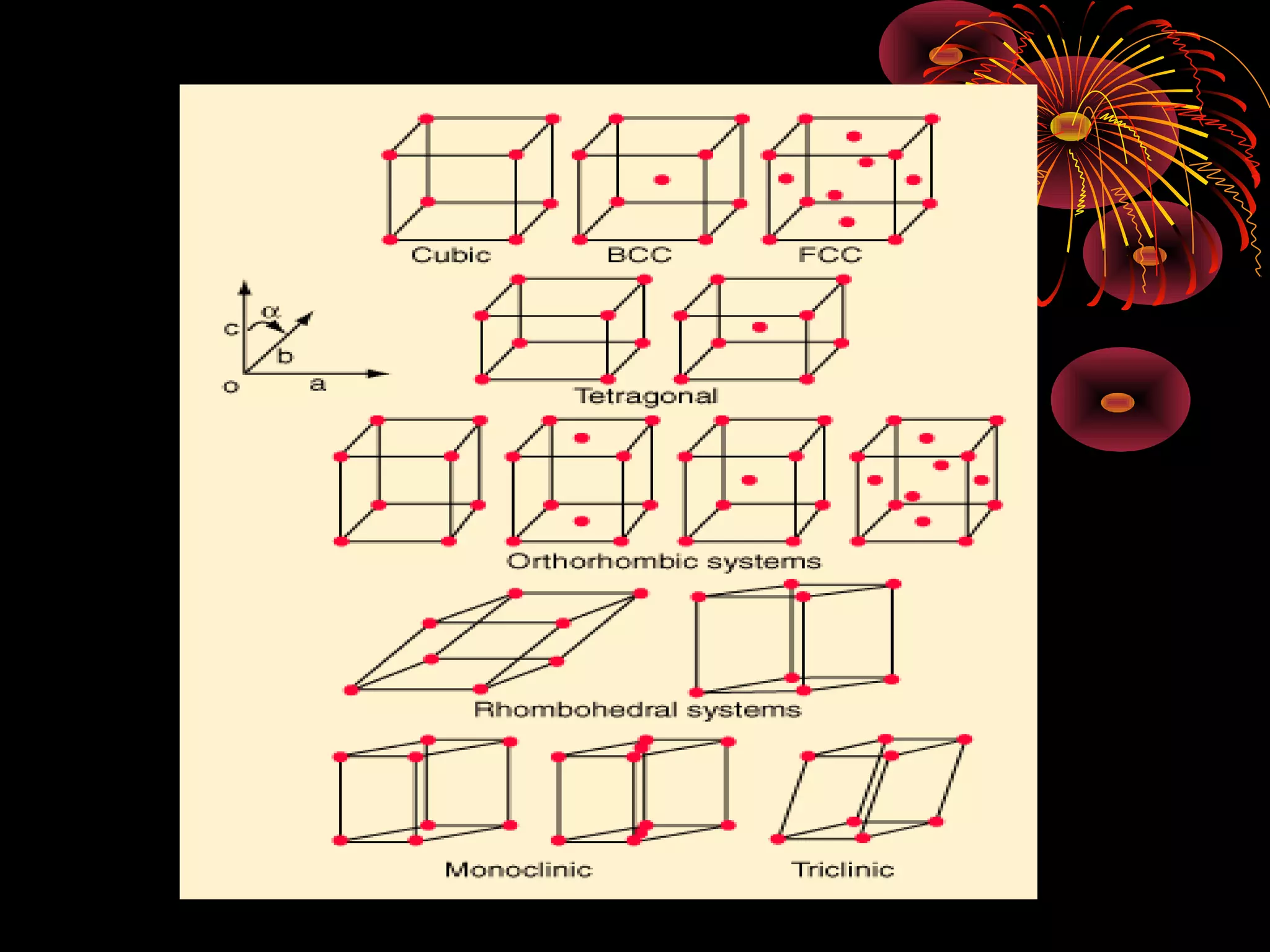
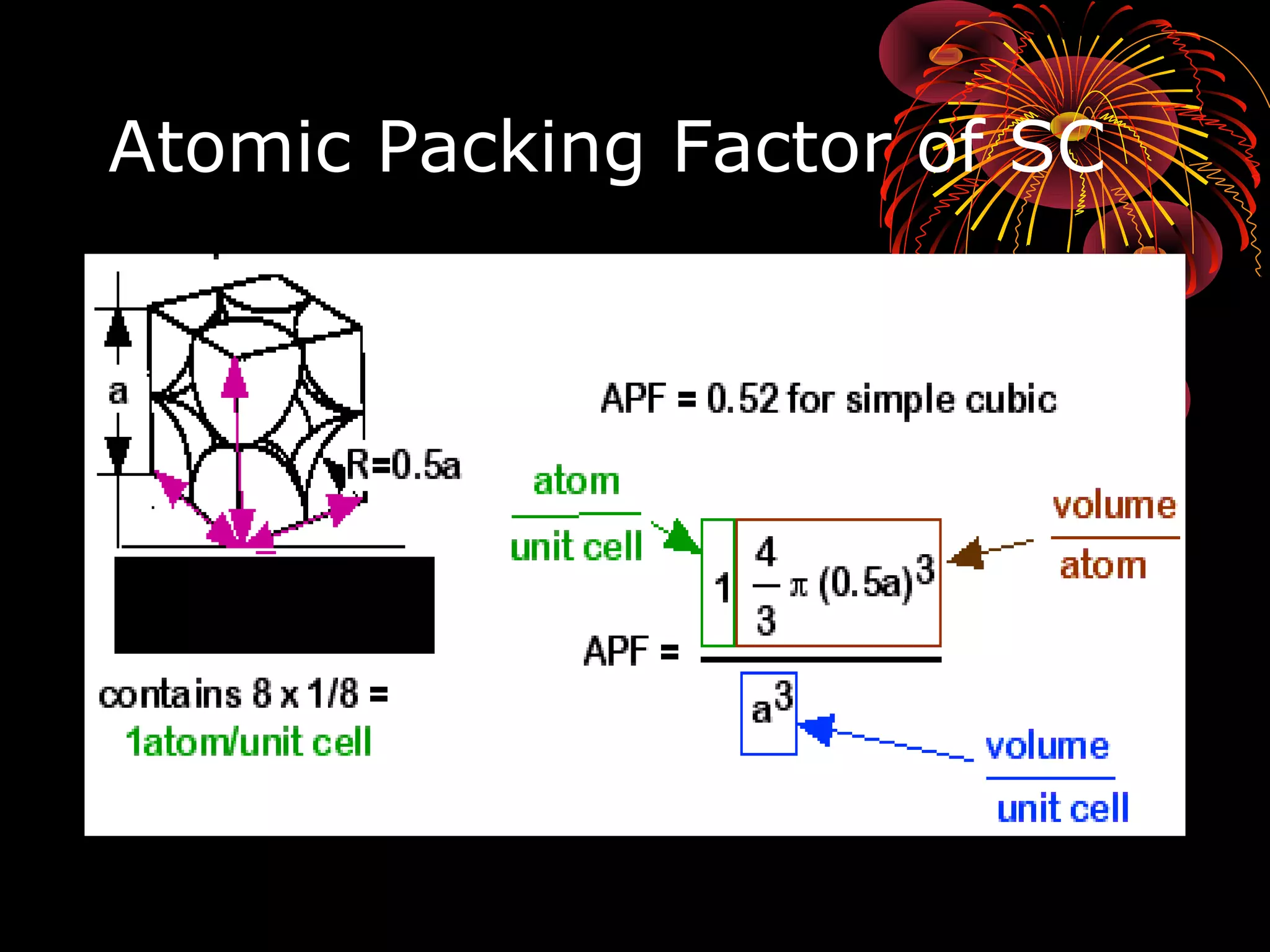
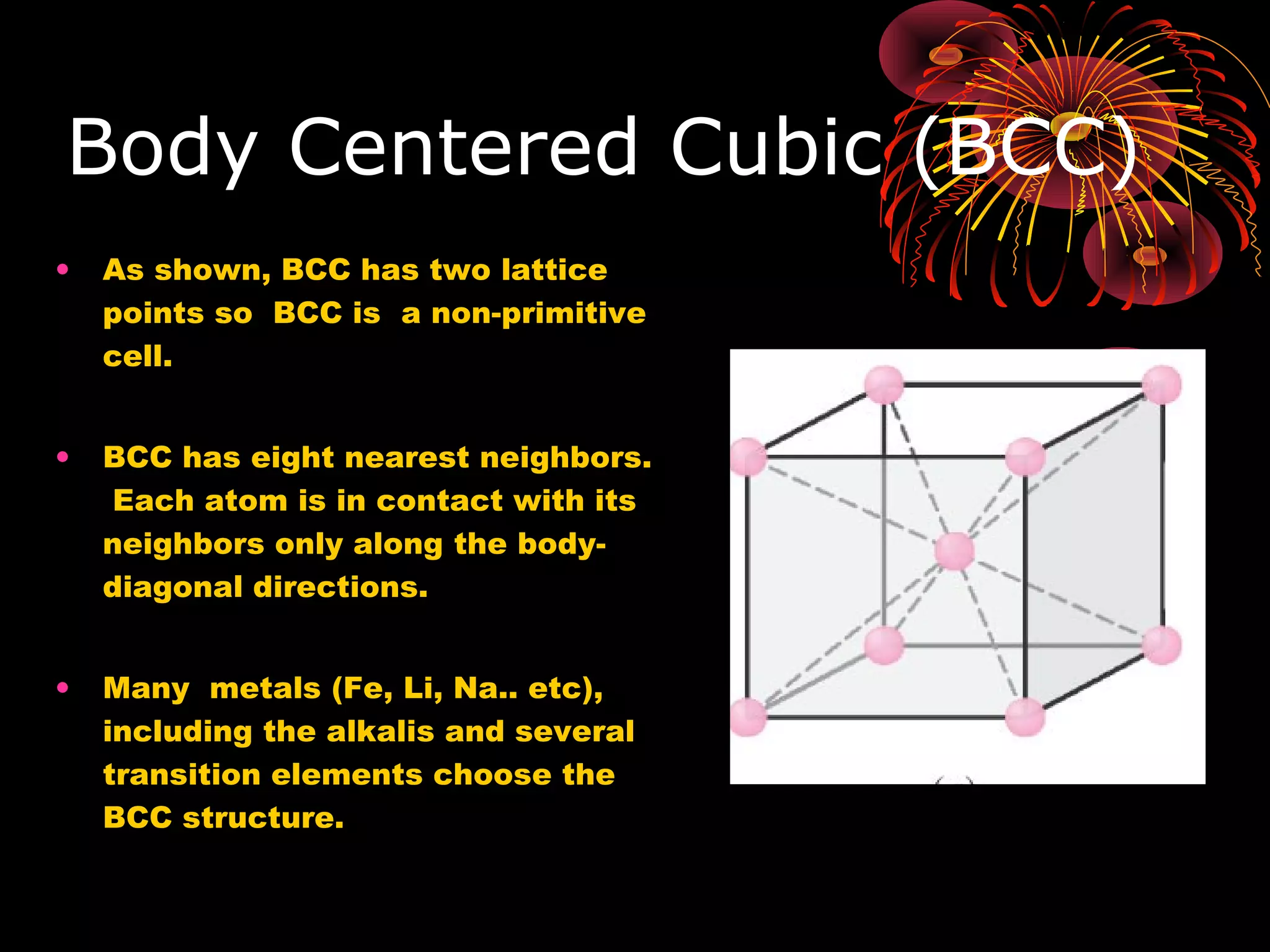
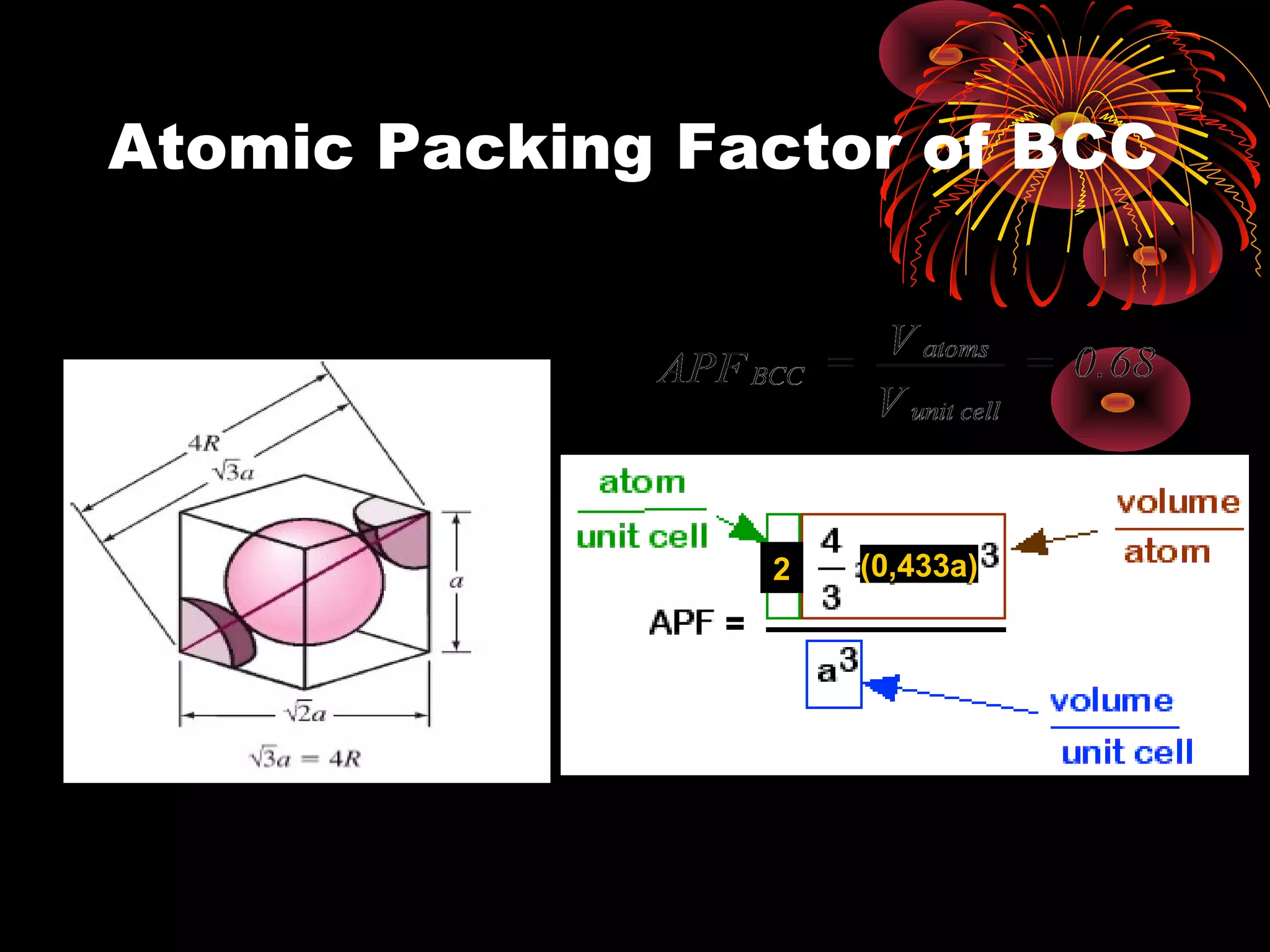
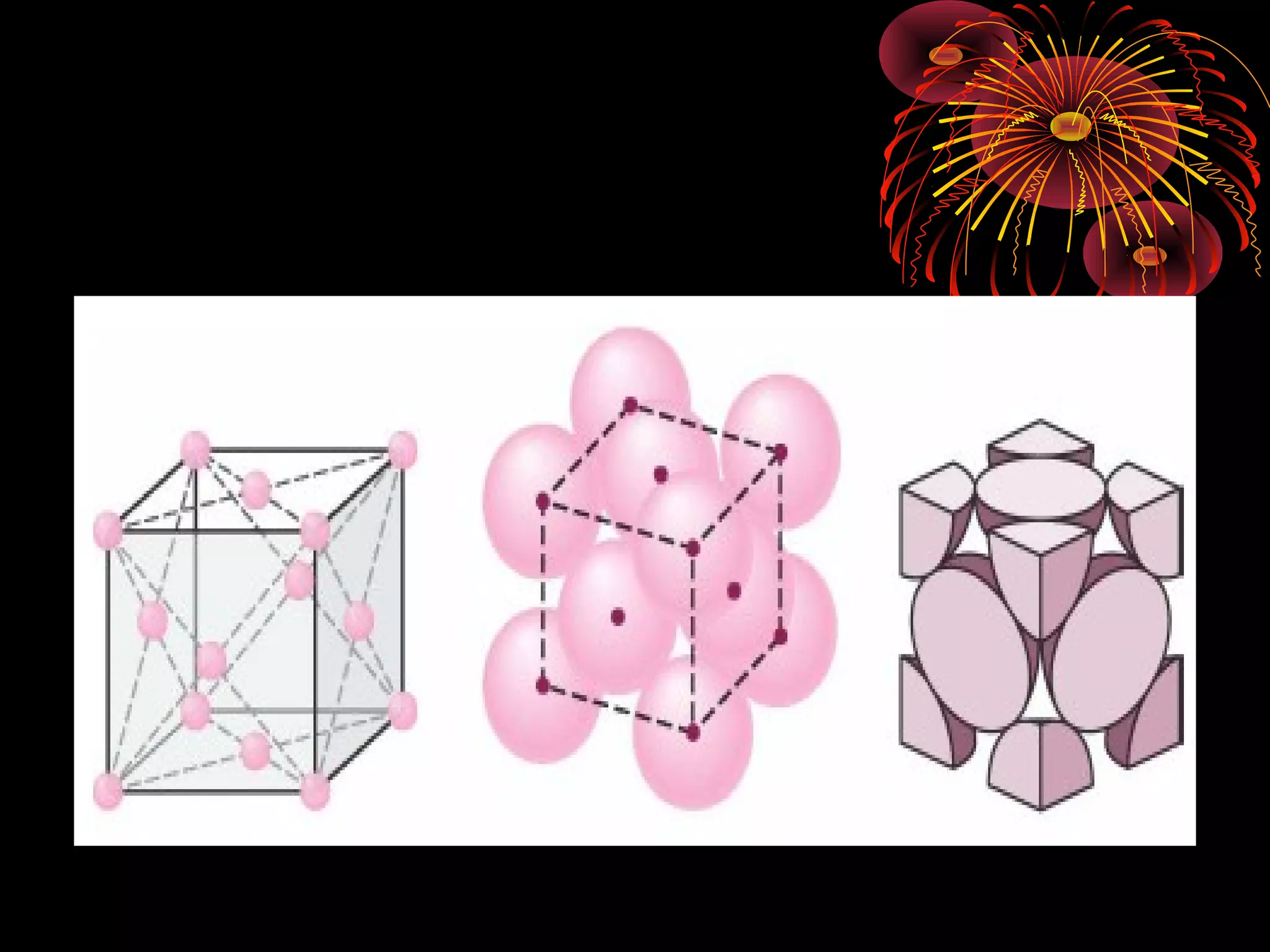
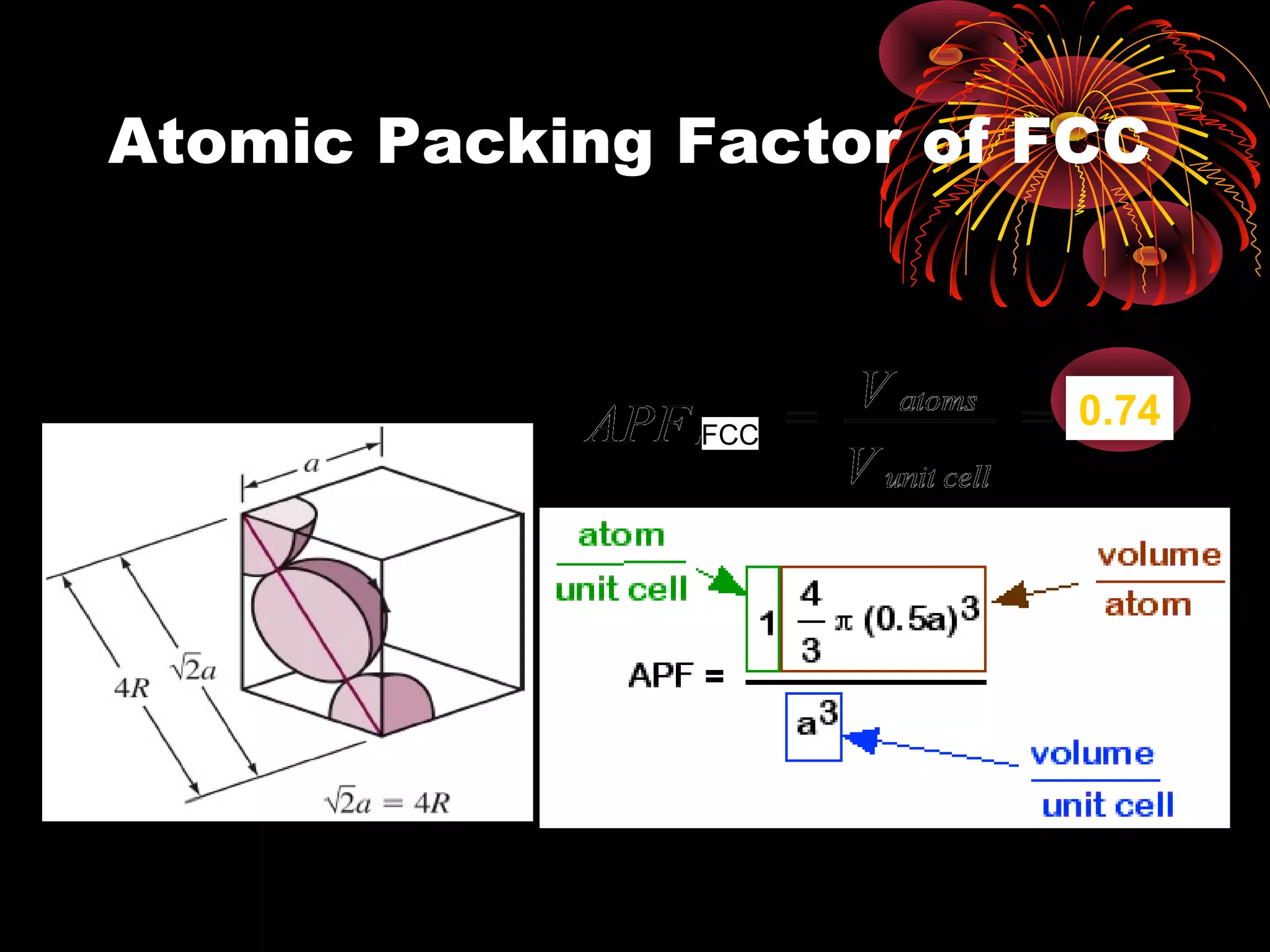
This document discusses crystal structures and x-ray diffraction. It defines crystalline and amorphous solids, unit cells, space lattices, and the seven crystal systems. It also explains Miller indices for identifying crystal planes and Bragg's law for x-ray diffraction, which relates the scattering angle θ, interplanar spacing d, wavelength λ, and order of reflection n. Crystals are characterized by their long-range ordered atomic arrangements, which can be analyzed using techniques like x-ray crystallography.

1. CRYSTAL STRUCTURE
&
X-RAY DIFFRACTION
Dr. Y. NARASIMHA MURTHY Ph.D
SRI SAI BABA NATIONAL COLLEGE (Autonomous)
ANANTAPUR-515001-A.P(INDIA)
yayavaram@yahoo.com

2. Classification of Matter

3. Solids
Solids are again classified in to two
types
 Crystalline
 Non-Crystalline (Amorphous)

4. What is a Crystalline solid?
A crystal or crystalline solid is a solid
material, whose constituent atoms,
molecules, or ions are arranged in an
orderly repeating pattern extending in
all three spatial dimensions.
So a crystal is characterized by regular
arrangement of atoms or molecules

5. Examples !
• Non-Metallic crystals:
Ice, Carbon, Diamond, Nacl, Kcl
etc…
• Metallic Crystals:
Copper, Silver, Aluminium, Tungsten,
Magnesium etc…

6. Crystalline Solid

7. Single crystal
Single Crystal
example

8. Amorphous Solid
• Amorphous (Non-crystalline) Solid is
composed of randomly orientated atoms ,
ions, or molecules that do not form
defined patterns or lattice structures.
• Amorphous materials have order only within
a few atomic or molecular dimensions.

9. • Amorphous materials do not have
any long-range order, but they have
varying degrees of short-range order.
• Examples to amorphous materials
include amorphous silicon, plastics,
and glasses.
• Amorphous silicon can be used in
solar cells and thin film transistors.

10. Non-crystalline

11. What are the Crystal properties?
o Crystals have sharp melting points
o They have long range positional order
o Crystals are anisotropic
(Properties change depending on the
direction)
o Crystals exhibit Bi-refringence
o Some crystals exhibit piezoelectric effect
& Ferroelectric effect etc…also

12. What is Space lattice ?
• An infinite array of
points in space,
• Each point has
identical
surroundings to all
others.
• Arrays are
arranged exactly
in a periodic
manner.
α
a
b
CB ED
O A
y
x

13. Translational Lattice Vectors – 2D
A space lattice is a set of
points such that a translation
from any point in the lattice by
a vector;
R = l a + m b
locates an exactly equivalent
point, i.e. a point with the
same environment as P . This
is translational symmetry. The
vectors a, b are known as
lattice vectors and (l,m) is a
pair of integers whose values
depend on the lattice point.

14. • For a three dimensional lattice
R = la + mb +nc
Here a, b and c are non co-planar vectors
• The choice of lattice vectors is not
unique. Thus one could equally well take
the vectors a, b and c as a lattice vectors.

15. Basis & Unit cell
• A group of atoms or molecules
identical in composition is called the
basis
or
• A group of atoms which describe
crystal structure

16. Unit Cell
• The smallest component of the
crystal (group of atoms, ions or
molecules), which when stacked
together with pure translational
repetition reproduces the whole
crystal.

17. S
S
a
S
S

18. 2D Unit Cell example -(NaCl)

19. Choice of origin is arbitrary - lattice
points need not be atoms - but unit
cell size should always be the same.

20. This is also a unit cell -
it doesn’t matter if you start from Na or Cl

21. This is NOT a unit cell even though
they are all the same - empty space is
not allowed!

22. In 2Dimensional space this is a unit cell
but in 3 dimensional space it is NOT

23. Now Crystal structure !!
Crystal lattice + basis = Crystal structure
• Crystal structure can be obtained by
attaching atoms, groups of atoms or
molecules which are called basis (motif)
to the lattice sides of the lattice point.

24. The unit cell and,
consequently, the
entire lattice, is
uniquely
determined by the
six lattice
constants: a, b, c,
α, β and γ. These
six parameters are
also called as basic
lattice parameters.

25. Primitive cell
• The unit cell formed by the primitives a,b
and c is called primitive cell. A primitive
cell will have only one lattice point. If
there are two are more lattice points it is
not considered as a primitive cell.
• As most of the unit cells of various crystal
lattice contains two are more lattice
points, its not necessary that every unit
cell is primitive.

27. Crystal systems
• We know that a three dimensional
space lattice is generated by repeated
translation of three non-coplanar
vectors a, b, c. Based on the lattice
parameters we can have 7 popular
crystal systems shown in the table

28. Table-1
Crystal system Unit vector Angles
Cubic a= b=c α =β =√=90
Tetragonal a = b≠ c α =β =√=90
Orthorhombic a ≠ b ≠ c α =β =√=90
Monoclinic a ≠ b ≠ c α =β =90 ≠√
Triclinic a ≠ b ≠ c α ≠ β ≠√ ≠90
Trigonal a= b=c α =β =√≠90
Hexagonal a= b ≠ c α =β=90
√=120

29. Bravais lattices
• In 1850, M. A. Bravais showed that
identical points can be arranged
spatially to produce 14 types of regular
pattern. These 14 space lattices are
known as ‘Bravais lattices’.

30. 14 Bravais lattices
S.No Crystal Type Bravais
lattices
Symbol
1 Cubic Simple P
2 Body
centred
I
3 Face
centred
F
4 Tetragonal Simple P
5 Body
centred
I
6 Orthorhombic Simple P
7 Base
centred
C

31. 8 Body
centred
I
9 Face
centred
F
10 Monoclinic Simple P
11 Base
centred
C
12 Triclinic Simple P
13 Trigonal Simple P
14 Hexgonal Simple P

33. Coordination Number
• Coordination Number (CN) : The Bravais
lattice points closest to a given point are
the nearest neighbours.
• Because the Bravais lattice is periodic, all
points have the same number of nearest
neighbours or coordination number. It is a
property of the lattice.
• A simple cubic has coordination number 6;
a body-centered cubic lattice, 8; and a face-
centered cubic lattice,12.

34. Atomic Packing Factor
• Atomic Packing Factor (APF) is
defined as the volume of atoms
within the unit cell divided by the
volume of the unit cell.

35. Simple Cubic (SC)
• Simple Cubic has one lattice point so its
primitive cell.
• In the unit cell on the left, the atoms at the
corners are cut because only a portion (in
this case 1/8) belongs to that cell. The rest of
the atom belongs to neighboring cells.
• Coordinatination number of simple cubic is 6.

36. a
b
c

37. Atomic Packing Factor of SC

38. Body Centered Cubic (BCC)
• As shown, BCC has two lattice
points so BCC is a non-primitive
cell.
• BCC has eight nearest neighbors.
Each atom is in contact with its
neighbors only along the body-
diagonal directions.
• Many metals (Fe, Li, Na.. etc),
including the alkalis and several
transition elements choose the
BCC structure.

39. Atomic Packing Factor of BCC
2 (0,433a)

40. Face Centered Cubic (FCC)
• There are atoms at the corners of the unit
cell and at the center of each face.
• Face centered cubic has 4 atoms so its
non primitive cell.
• Many of common metals (Cu, Ni, Pb ..etc)
crystallize in FCC structure.

42. Face Centered Cubic (FCC)

43. Atomic Packing Factor of FCC
FCC
0.74

44. HEXAGONAL SYSTEM
 A crystal system in which three equal coplanar axes
intersect at an angle of 60, and a perpendicular to
the others, is of a different length.

45. TRICLINIC & MONOCLINIC CRYSTAL SYSTEMTRICLINIC & MONOCLINIC CRYSTAL SYSTEM
Triclinic minerals are the least symmetrical. Their
three axes are all different lengths and none of them
are perpendicular to each other. These minerals are
the most difficult to recognize.
Monoclinic (Simple)
α = γ = 90o
, ß ≠ 90o
a ≠ b ≠c
Triclinic (Simple)
α ≠ ß ≠ γ ≠ 90
o
a ≠ b ≠ c
Monoclinic (Base Centered)
α = γ = 90o
, ß ≠ 90o
a ≠ b ≠ c,

46. ORTHORHOMBIC SYSTEM
Orthorhombic (Simple)
α = ß = γ = 90o
a ≠ b ≠ c
Orthorhombic (Base-
centred)
α = ß = γ = 90o
a ≠ b ≠ c
Orthorhombic (BC)
α = ß = γ = 90o
a ≠ b ≠ c
Orthorhombic (FC)
α = ß = γ = 90o
a ≠ b ≠ c

47. TETRAGONAL SYSTEM
Tetragonal (P)
α = ß = γ = 90o
a = b ≠ c
Tetragonal (BC)
α = ß = γ = 90o
a = b ≠ c

48. Rhombohedral (R) or Trigonal
Rhombohedral (R) or Trigonal (S)
a = b = c, α = ß = γ ≠ 90o

49. Crystal Directions
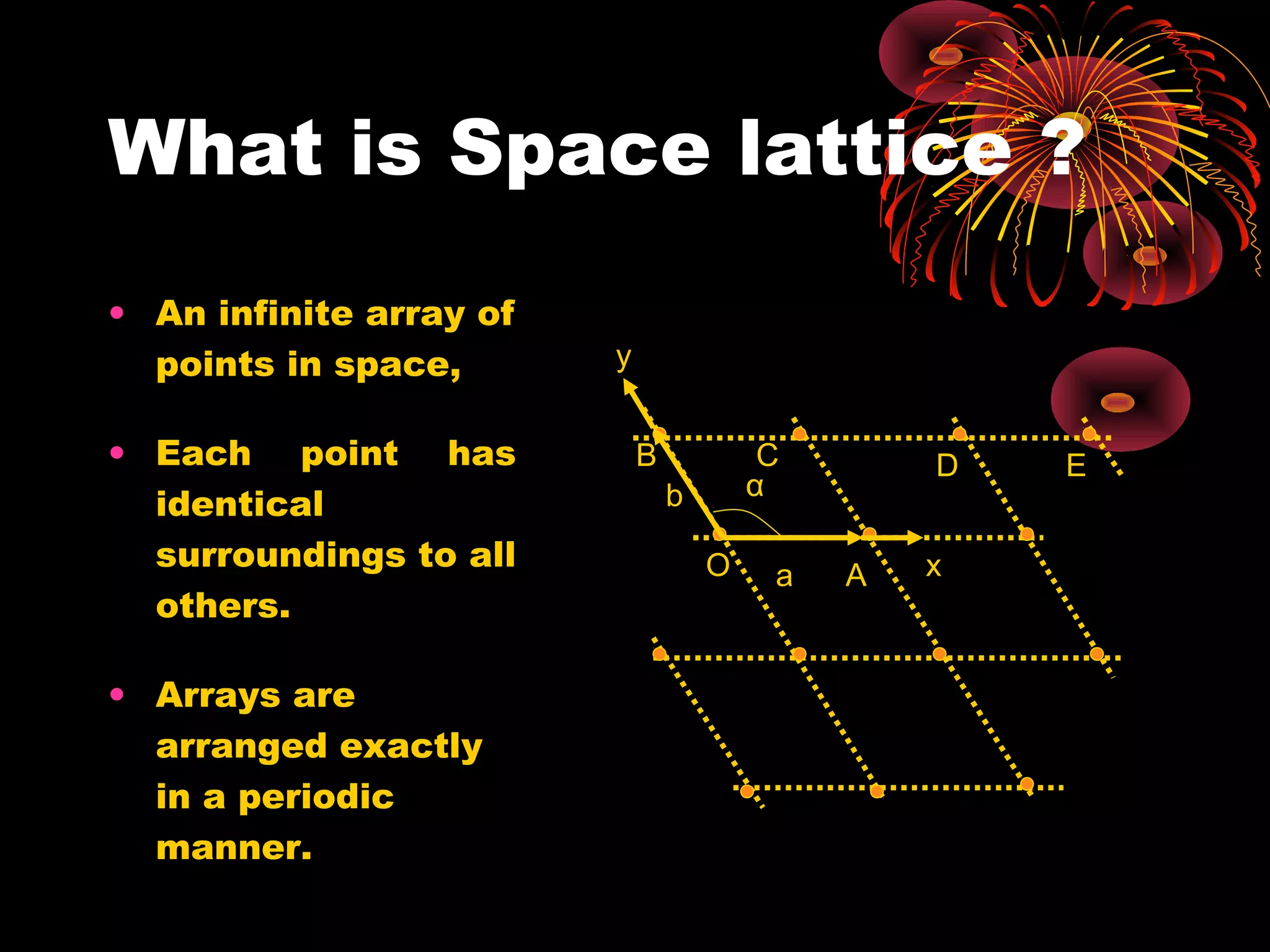
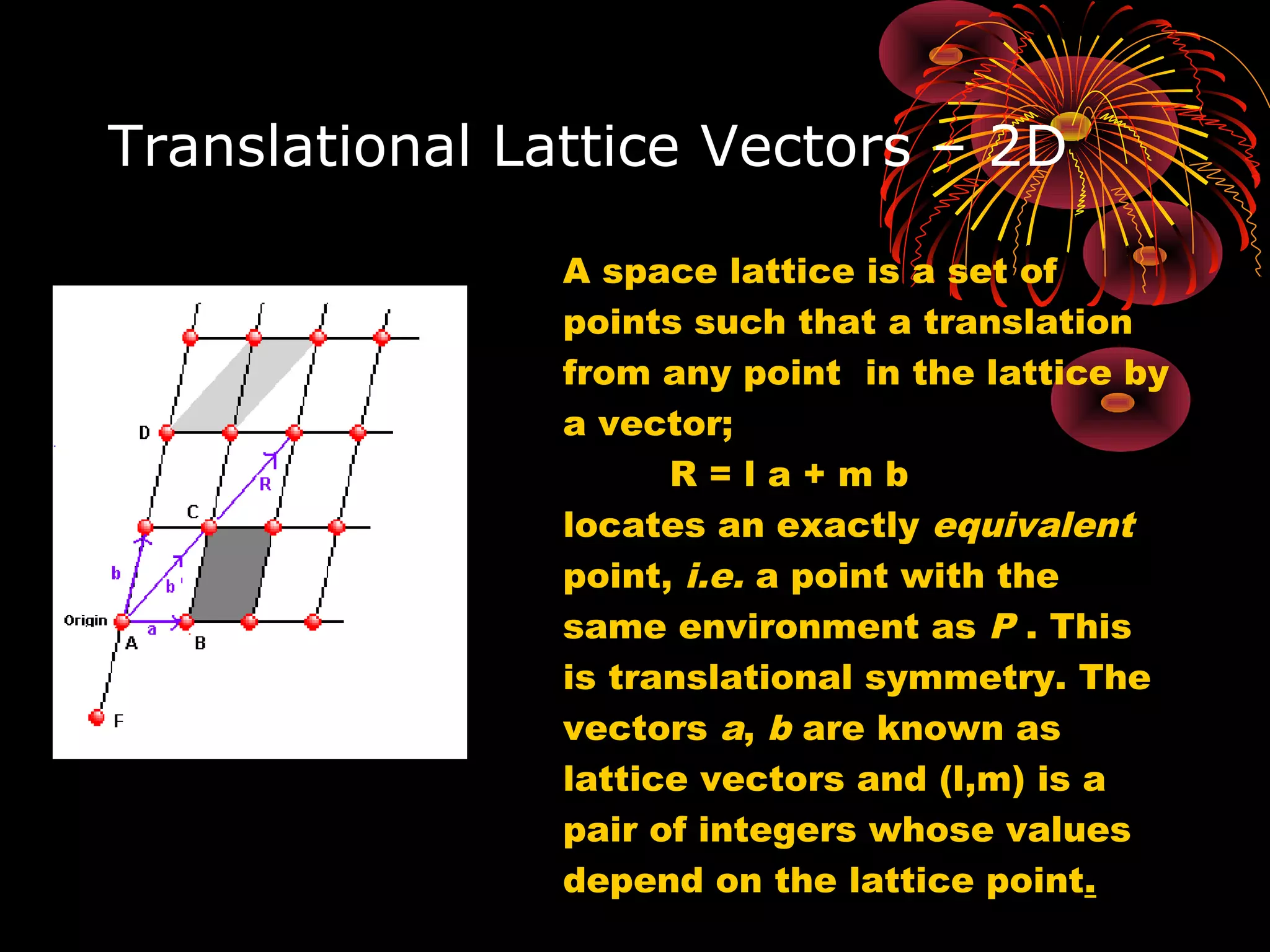
• We choose one lattice point on the line as an origin, say
the point O. Choice of origin is completely arbitrary, since
every lattice point is identical.
• Then we choose the lattice vector joining O to any point on
the line, say point T. This vector can be written as;
R = la + mb + nc
To distinguish a lattice direction from a lattice point, the
triple is enclosed in square brackets [ ... ] is used. [l, m, n]
• [l, m, n] is the smallest integer of the same relative ratios.

50. 210
X = 1 , Y = ½ , Z = 0
[1 ½ 0] [2 1 0]

51. Negative directions
• When we write the
direction [n1n2n3]
depend on the origin,
negative directions can
be written as
• R = l a + m b + n c
• Direction must be
smallest integers.

52. Examples of crystal directions
X = 1 , Y = 0 , Z = 0 ► [1 0 0]

53. Crystal Planes
• Within a crystal lattice it is possible to identify sets
of equally spaced parallel planes. These are called
lattice planes.
• In the figure density of lattice points on each plane
of a set is the same and all lattice points are
contained on each set of planes.
b
a
b
a

54. MILLER INDICES FOR
CRYSTALLOGRAPHIC PLANES
• William HallowesMiller in 1839 was able to
give each face a unique label of three
small integers, the Miller Indices
• Definition: Miller Indices are the
reciprocals of the fractional intercepts
(with fractions cleared) which the plane
makes with the crystallographic x,y,z axes
of the three nonparallel edges of the cubic
unit cell.

55. Miller Indices
Miller Indices are a symbolic vector representation for the
orientation of an atomic plane in a crystal lattice and are
defined as the reciprocals of the fractional intercepts which
the plane makes with the crystallographic axes.
To determine Miller indices of a plane, we use the following
steps
1) Determine the intercepts of the plane along each
of the three crystallographic directions
2) Take the reciprocals of the intercepts
3) If fractions result, multiply each by the
denominator of the smallest fraction

56. IMPORTANT HINTS:
• When a plane is parallel to any
axis,the intercept of the plane
on that axis is infinity.So,the
Miller index for that axis is Zero
• A bar is put on the Miller index
when the intercept of a plane on
any axis is negative
• The normal drawn to a plane
(h,k,l) gives the direction [h,k,l]

57. Example-1
(1,0,0)

58. Example-2
(1,0,0)
(0,1,0)

59. Example-3
(1,0,0)
(0,1,0)
(0,0,1)

60. Example-4
(1/2, 0, 0)
(0,1,0)

61. Miller Indices

62. Spacing between planes in a
cubic crystal is
l+k+h
a
=d 222
hkl
Where dhkl = inter-planar spacing between planes with Miller
indices h, k and l.
a = lattice constant (edge of the cube)
h, k, l = Miller indices of cubic planes being considered.

63. X-Ray diffraction
• X-ray crystallography, also called X-ray
diffraction, is used to determine crystal
structures by interpreting the diffraction
patterns formed when X-rays are scattered
by the electrons of atoms in crystalline
solids. X-rays are sent through a crystal to
reveal the pattern in which the molecules
and atoms contained within the crystal are
arranged.

64. • This x-ray crystallography was developed
by physicists William Lawrence Bragg and
his father William Henry Bragg. In 1912-
1913, the younger Bragg developed
Bragg’s law, which connects the observed
scattering with reflections from evenly
spaced planes within the crystal.

65. X-Ray Diffraction
Bragg’s Law : 2dsinΘ = nλ