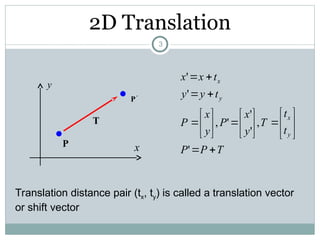
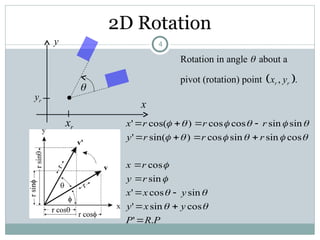
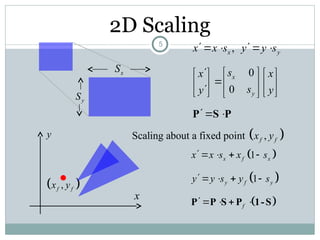
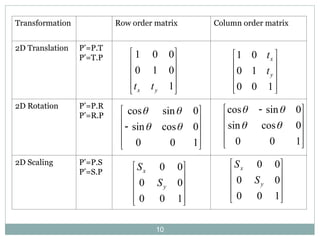
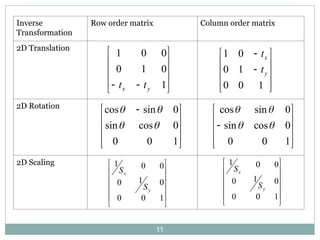
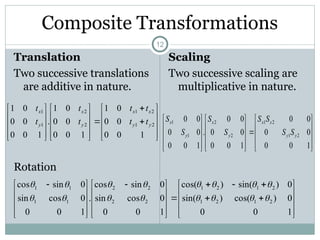
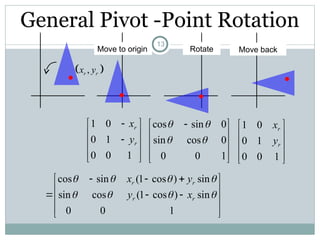
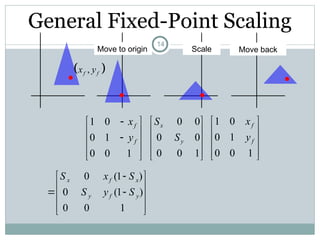
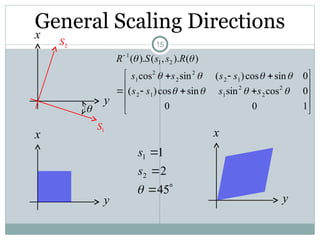
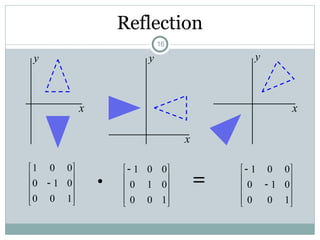
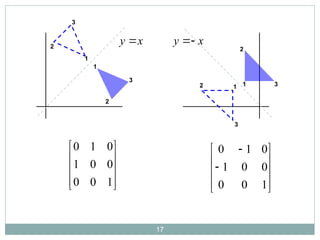
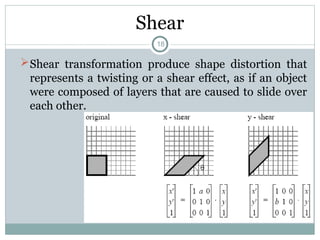
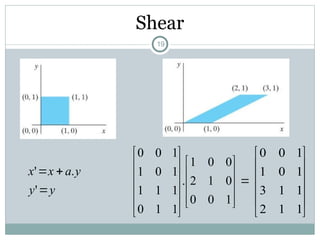
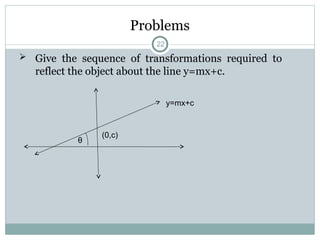
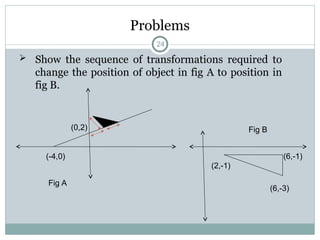
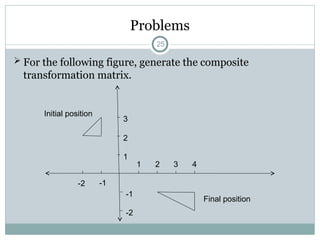
The document discusses two-dimensional geometric transformations, including translation, rotation, scaling, and shear. It explains the use of homogeneous coordinates for efficient transformations and the mathematical representations for each type. The text also covers composite transformations and practical problems related to applying these concepts.

1. PROF. SONAL SHROFF
COMPUTER ENGG DEPT
TSEC
Two Dimensional Geometric
Transformations

2. Basic Transformations
 Translation
 A translation is applied to an object by repositioning it
along a straight-line path from one coordinate location to
another.
 Rotation
 A rotation is applied to an object by repositioning it along a
circular path in the xy plane.
 Scaling
 A scaling transformation alters the size of object.
2

3. 2D Translation
P

P
T
x
y
Translation distance pair (tx, ty) is called a translation vector
or shift vector
T
P
P
t
t
T
y
x
P
y
x
P
t
y
y
t
x
x
y
x
y
x



























'
,
'
'
'
,
'
'
3

4. 2D Rotation
x
y
r
x
r
y

 
Rotation in angle about a
pivot (rotation) point , .
r r
x y

P
R
P
y
x
y
y
x
x
r
y
r
x
r
r
r
y
r
r
r
x
.
'
cos
sin
'
sin
cos
'
sin
cos
cos
sin
sin
cos
)
sin(
'
sin
sin
cos
cos
)
cos(
'

































4

5. 2D Scaling
x
S
y
S
,
0
0
x y
x
y
x x s y y s
s
x x
s
y y
 
   
  
   
 
   

   
 
 
P S P
x
y
 
,
f f
x y
 
 
 
1
1
x f x
y f y
f
x x s x s
y y s y s
   
   
   
P P S P 1-S
 
Scaling about a fixed point ,
f f
x y
5

6. Homogeneous Coordinates
Many graphics applications involve sequence of
geometric transformations.
Animation – may require an object to be translated
and rotated at each increment of the motion.
1 2
1 2
Rotate and then displace a point :
: 2 2 rotation matrix. : 2 1 displacement vector.
 
 
P P = M P + M
M M
6

7. Homogeneous Coordinates
A more efficient approach would be to combine the
transformations so that the final coordinate positions
are obtained directly from the initial coordinates,
thereby eliminating the calculation of intermediate
coordinate values.
To do this, we need to reformulate the coordinate
representation.
To express any 2D-transformation as a matrix
multiplication, we express each Cartesian coordinate
point (x,y) as homogeneous coordinate triple(xh, yh, h)
where x = xh/h and y= yh/h
7

8. Homogeneous Coordinates
In general, (x.h, y.h, h)
For 2D geometric transformations h = any non zero
value
Thus, there are an infinite number of equivalent
homogeneous representations for each cartesian
coordinate point (x,y).
A convenient choice is h = 1.
Thus (x,y) is represented as (x,y,1)
8

9. Homogeneous Coordinates
   
Make displacement linear with .
, , ,1 . Transformations turn into 3 3 matrices.
x y x y
 
Homoheneous Coordinates
Very big advantage. All transformations are concatenated by
matrix multiplication.
9

10. 









1
0
1
0
0
0
1
y
x t
t
Transformation Row order matrix Column order matrix
2D Translation P’=P.T
P’=T.P
2D Rotation P’=P.R
P’=R.P
2D Scaling P’=P.S
P’=S.P










1
0
0
1
0
0
1
y
x
t
t











1
0
0
0
cos
sin
0
sin
cos














1
0
0
0
0
0
0
y
x
S
S










1
0
0
0
0
0
0
y
x
S
S









 
1
0
0
0
cos
sin
0
sin
cos




10

11. 










 1
0
1
0
0
0
1
y
x t
t
Inverse
Transformation
Row order matrix Column order matrix
2D Translation
2D Rotation
2D Scaling












1
0
0
1
0
0
1
y
x
t
t









 
1
0
0
0
cos
sin
0
sin
cos















1
0
0
0
cos
sin
0
sin
cos
















1
0
0
0
1
0
0
0
1
y
x
S
S












1
0
0
0
1
0
0
0
1
y
x
S
S
11

12. Composite Transformations
Translation
Two successive translations
are additive in nature.
Rotation
Scaling
Two successive scaling are
multiplicative in nature.

































1
0
0
0
0
0
1
1
0
0
0
0
0
1
.
1
0
0
0
0
0
1
2
1
2
1
2
2
1
1
y
y
x
x
y
x
y
x
t
t
t
t
t
t
t
t































1
0
0
0
0
0
0
1
0
0
0
0
0
0
.
1
0
0
0
0
0
0
2
1
2
1
2
2
1
1
y
y
x
x
y
x
y
x
S
S
S
S
S
S
S
S

























 









 
1
0
0
0
)
cos(
)
sin(
0
)
sin(
)
cos(
1
0
0
0
cos
sin
0
sin
cos
.
1
0
0
0
cos
sin
0
sin
cos
2
1
2
1
2
1
2
1
2
2
2
2
1
1
1
1
















12

13. General Pivot -Point Rotation
Move to origin Rotate Move back
 
,
r r
x y









 
1
0
0
0
cos
sin
0
sin
cos














1
0
0
1
0
0
1
r
r
y
x












1
0
0
1
0
0
1
r
r
y
x
















1
0
0
sin
)
cos
1
(
cos
sin
sin
)
cos
1
(
sin
cos








r
r
r
r
x
y
y
x
13

14. General Fixed-Point Scaling
Move to origin Scale Move back
 
,
f f
x y










1
0
0
1
0
0
1
f
f
y
x










1
0
0
0
0
0
0
y
x
S
S












1
0
0
1
0
0
1
f
f
y
x













1
0
0
)
1
(
0
)
1
(
0
y
f
y
x
f
x
S
y
S
S
x
S
14

15. General Scaling Directions
y
x
2
S
1
S

y
x
y
x


















1
0
0
0
cos
sin
sin
cos
)
(
0
sin
cos
)
(
sin
cos
)
(
).
,
(
).
(
2
2
2
1
1
2
1
2
2
2
2
1
2
1
1










s
s
s
s
s
s
s
s
R
s
s
S
R




45
2
1
2
1

s
s
15

16. Reflection
x
y
x
y
x
y











1
0
0
0
1
0
0
0
1












1
0
0
0
1
0
0
0
1










1
0
0
0
1
0
0
0
1
16

17. 1
2
3
y x
 y x

1
2
3
3
1
2










1
0
0
0
0
1
0
1
0
1
2
3












1
0
0
0
0
1
0
1
0
17

18. Shear
Shear transformation produce shape distortion that
represents a twisting or a shear effect, as if an object
were composed of layers that are caused to slide over
each other.
18

19. Shear























1
0
0
0
1
2
0
0
1
.
1
1
0
1
1
1
1
0
1
1
0
0
y
y
y
a
x
x



'
.
'












1
1
2
1
1
3
1
0
1
1
0
0
19

20. 






















1
0
0
0
1
0
0
2
1
.
1
1
0
1
1
1
1
0
1
1
0
0
y
x
b
y
x
x



.
'
'























1
0
0
0
1
2
0
2
1
.
1
1
0
1
1
1
1
0
1
1
0
0
y
x
b
y
y
a
x
x




.
'
.
'












1
1
0
1
3
1
1
2
1
1
0
0












1
2
1
1
3
3
1
1
2
1
0
0
20

21. Problems
 Rotate the polygon whose vertices are A(0,0),
B(0,2), C(2,2) and D(2,0) about an origin by
rotation angle θ=45˚
21

22. Problems
 Give the sequence of transformations required to
reflect the object about the line y=mx+c.
θ
(0,c)
y=mx+c
22

23. Problems
 Rotate the polygon whose vertices are A(0,0),
B(1,2), C(2,2) and D(2,1) about a point(1,1) by
rotation angle θ=45˚
23

24. Problems
 Show the sequence of transformations required to
change the position of object in fig A to position in
fig B.
24
(-4,0)
(0,2)
(2,-1)
(6,-3)
(6,-1)
Fig A
Fig B

25. Problems
 For the following figure, generate the composite
transformation matrix.
1
2
3
1 2 3 4
-1
-2
-1
-2
Initial position
Final position
25