The document discusses fundamental concepts of geometric transformations in computer graphics, including translation, rotation, scaling, reflection, and shear, and their applications in modeling and animation. It covers the mathematical representation of these transformations using matrices and homogeneous coordinates, as well as composite transformations. Examples and equations are provided to illustrate the application of these transformations in various scenarios.

1. 1
CHAPTER 2.1 : FUNDAMENTAL OF COMPUTER GRAPHICS
Prof. RATNADEEPSINH M. JADEJA
Assistant Professor
Mechanical Department

2. Mechanical Engineering Department – School Of Engineering
GEOMETRIC TRANSFORMATIONS
2
All the changes performed on the graphic image are done by changing the database of
the original picture.
These changes are called as transformations.
Geometric transformations are used for the following purposes:
1. They are a must in the creation of a model, or the purpose of viewing it.
2. They are used to express location of objects relative to others.
3. Geometric transformations can be used to view an object from different positions and
directions.
4. They can be used to perform certain transformations such as translate/move, rotate,
scale and mirror.
5. They can also be used to obtain orthographic and perspective views of a model.
6. Geometrical Transformations with the help of kinematic analysis can be used to create
animation to study the motion of the model.

3. Mechanical Engineering Department – School Of Engineering
FORMULATION
3
P2(x2,y2)
P1(x1,y1)
Y
X
X2
X1
Y2
Y1
A point represented by a 1 × 2 matrix
P1 = [x1,y1]
Similarly, a line can be represented as :
L =
1
2
=
1 1
2 2
Line represented after transformation
L’ = L [TM]
Where, [TM] = Transformation Matrix
0

4. Mechanical Engineering Department – School Of Engineering
TRANSLATION
4
(x1, y1)
(x2, y2)
(x1’, y1’)
(x2’, y2’)
Translation Matrix T = [tx ty]
Equation of line L =
1 1
2 2
Transferred line represented as
L’ = L + [T] =
1 1
2 2
+ [tx ty]
X
Y
0

5. Mechanical Engineering Department – School Of Engineering
TRANSLATION
5
A(1,1)
B(7,3)
C(1,4)
A(4,3)
B(4,1)
C(4,6)
A triangle translated 3 unit in x direction and 2
unit in y direction.
Triangle ABC represented as
ΔABC =
1 1
4 1
1 4
Translation equation of triangle is
ΔA’B’C’ = ΔABC + [tx ty]
ΔA’B’C’ =
1 1
4 1
1 4
+ [3 2]
=
4 3
7 3
4 6
X0
Y

6. Mechanical Engineering Department – School Of Engineering
ROTATION
6
X
Y
P(x,y)
P’(x’,y’)
r
r
x=r cosф
y=rsinф
X’=r cos(Ɵ+ф)
y’=rsin(Ɵ+ф)
ф
Ɵ
Point P is represented as
P = [x y]
= [r cos ф r sin ф]
The rotated point be represented as :
P’ = [r cos(Ɵ+ф) r sin(Ɵ+ф)]
= [r (cos Ɵcos ф – sinƟ sin ф) r (sin Ɵ cos ф + cos
Ɵ sin ф )
= [(x cos Ɵ – y sin Ɵ) (x sin Ɵ + y cos Ɵ)
This can be expressed as :
P’ = [x y]
cos Ɵ sin Ɵ
− Ɵ cos Ɵ
= = P × [R]
where R is rotation matrix
R =
cos Ɵ sin Ɵ
− Ɵ cos Ɵ
If rotation is anticlockwise then Ɵ is +VE
If rotation is clockwise then Ɵ is -VE

7. Mechanical Engineering Department – School Of Engineering
SCALING
7
B’(4,2)
A(1,1)
C(1,2)
A’(2,2)
B(2,1)
C’(2,4)
X0
Y Scaling transformation alters the size of the object.
Scaling can be uniform(in X and Y direction) or non-
uniform (either in x direction or in Y direction.
Scaling in X = Sx
Scaling in Y = Sy
Example: A uniform scaling factor Sx = Sy = 2
ΔA’B’C’ = ΔABC · S
ΔA’B’C’ =
1 1
2 1
1 2
·
0
0
=
2 2
4 2
2 4

8. Mechanical Engineering Department – School Of Engineering
REFLECTION (MIRROR)
8
Reflection transformation equation.
P’ = P · M
Where M is a reflection matrix
X
Y
1 2
3
1’2’
3’
(a) Reflection about Y axis
M =
−1 0
0 1
1 2
3
1’ 2’
3’
(b) Reflection about X axis
M =
1 0
0 −1 1 2
3
1’
2’ 3’ (c) Reflection about y = x axis
M =
0 1
1 0
Reflection is the process of obtaining a mirror of the original shape

9. Mechanical Engineering Department – School Of Engineering
REFLECTION (MIRROR)
9
Reflection is the process of obtaining a mirror of the original shape
Reflection transformation equation.
P’ = P · M
Where M is a reflection matrix
X
Y
(d) Reflection about y = -x
M =
0 −1
−1 0
(e) Reflection about x and y axis
M =
−1 0
0 −1
X
Y
1 2
3
1’
2’3’
1 2
3
1’2’
3’
1’’2’’
3’’

10. Mechanical Engineering Department – School Of Engineering
SHEAR
10
This transformation causes the image to slant.
The y shear preserves all the x coordinate values
but shifts the y values.
The x shear preserves all the y coordinate values
but shifts the x values.
P’ = P · SH
SH =
1
0 1
for y shear
SH =
1 0
1
for x shear
X
Y
A B
CD
A’ B’
C’D’

11. Mechanical Engineering Department – School Of Engineering
HOMOGENEOUS COORDINATES
11
P (x, y) which can be expressed as P (x’ y’ h)
Where x = x’/h and y = y’/h
Where h is non zero number. A convenient value for h = 1.
So in homogeneous coordinate system point P is expressed as P (x, y, 1)
The general transformation matrix is also modified to a 3 × 3 matrix expressed in the form :
0
0
1

12. Mechanical Engineering Department – School Of Engineering
e). Shear :
HOMOGENEOUS COORDINATES
12
The important matrix transformations in the homogeneous coordinate system will now be modified as under.
T =
1 0 0
0 1 0
1
a). Translation : b). Rotation :
R =
Ɵ sin Ɵ 0
− sin Ɵ cos Ɵ 0
0 0 1
c). Scaling :
S =
0 0
0 0
0 0 1
d). Reflection / Mirror :
M =
0
0
0 0 1
For y shear, SHy =
1 0
0 1 0
0 0 1
For x shear, SHx =
1 0 0
1 0
0 0 1

13. Mechanical Engineering Department – School Of Engineering
INVERSE TRANSLATIONS
13
T =
0
0
1
Find out the inverse matrix of T
inv
0
0
1
=
− 0
− 0
− − −
inv
1 0 0
0 1 0
1
=
1 0 0
0 1 0
− − 1
Inverse Transformation for Translation:
Inverse Transformation for Rotation:
inv
cos Ɵ sin Ɵ 0
− sin Ɵ cos Ɵ 0
0 0 1
=
cos Ɵ − sin Ɵ 0
sin Ɵ cos Ɵ 0
0 0 1
=
cos(− Ɵ) sin(−Ɵ) 0
−sin(−Ɵ) cos(− Ɵ) 0
0 0 1
Inverse Transformation for Scaling:
inv
0 0
0 0
0 0 1
=
1/ 0 0
0 1/ 0
0 0 1

14. Mechanical Engineering Department – School Of Engineering
CONCATENATION OR COMPOSITE TRANSFORMATION
14
With homogeneous coordinates, composite transformations (more than one) can be done
by calculating the matrix product for all individual transformations.
First let us consider some properties of matrices.
1. As general rule, matrix multiplication is not commutative. A·B ≠ B · A
2. Matrix multiplication is associative. For any three matrices, A, B and C,
A · B · C = (A · B) · C = A · (B · C)

15. Mechanical Engineering Department – School Of Engineering
ROTATION ABOUT ANY POINT
15
1
1’
2
2’
3
3’
(a) Rotation about Origin
+
(a) Rotation about any given point

16. Mechanical Engineering Department – School Of Engineering
ROTATION ABOUT ANY POINT
16
+
P (x, y)
x
Y
a) Original shape
+
+
b) Translate to Origin
+
+
c) Rotation about Origin
+
d) Translate back to Original Point
P’ = P · T · R · (inv T)

17. Mechanical Engineering Department – School Of Engineering
SCALING ABOUT ANY POINT
17
+
P(X, Y)
X
Y
a) Original shape
+
b) Translation to Origin
+ +
+
c) Scaling about Origin
+
d) Translate back to Original Point
P’ = P · T · S · (inv T)

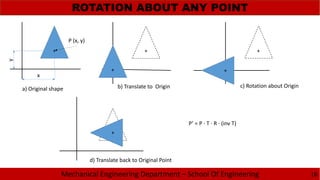
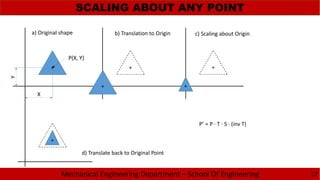
18. Mechanical Engineering Department – School Of Engineering
REFLECTION ABOUT ANY AXIS y = mx + c
18
a) Original Shape b) Translation to Origin
c) Rotation
d) Reflection
e) Inverse Rotation f) Inverse Translation
Original Image
Mirror Image
P’ = P · T · R · M · [inv R] · [inv T]

19. Mechanical Engineering Department – School Of Engineering
Example
19
Ex 1. A rectangle is formed by four points ABCD whose coordinates are: A (50, 50), B(100, 50),
C(100, 80) and D(50,80). Calculate the new coordinates of the rectangle in reduced size using
the scaling factors Sx = 0.5 and Sy = 0.6
Ans. =
25 30 1
50 30 1
50
25
48
48
1
1

20. Mechanical Engineering Department – School Of Engineering
Example
20
Ex 2. Write a 3 × 3 transformation matrix for the following effects:
a). Scale the image to be twice as large and then translate it 1 unit to the left.
b). Scale X direction to be half as large and then rotate anticlockwise by 90° about the origin
c). Rotate anticlockwise about origin by 90° and then scale the X direction by half as large.
d). Translate down 0.5 unit, right 0.5 unit, and then rotate anticlockwise by 45°.
Ans. = a) G = S · T
=
2 0 0
0 2 0
−1 0 1
Ans. = b) G = S · R
=
0 0.5 0
−1 0 0
0 0 1
Ans. = c) G = R · S
=
0 1 0
−0.5 0 0
0 0 1
Ans. = d) G = T · R
=
0.707 0.707 0
−0.707 0.707 0
0.707 0 1

21. Mechanical Engineering Department – School Of Engineering
Example
21
Ex. 3 A triangle ABC has its Vertices at A(0, 0), B(4, 0), and C(2, 3). It is to be translated by
4 units in X direction, and 2 units in Y direction, then it is to be rotated in anticlockwise
direction about the new position of point C through 90°. Find the new position of the
triangle
Ans. ΔA’B’C’ = ΔABC · T
=
4 2 1
8 2 1
6 5 1
ΔA’’B’’C’’ = ΔA’B’C’ · T · R · (inv T)
=
9 3 1
9 7 1
6 5 1

22. Mechanical Engineering Department – School Of Engineering
Example
22
Ex. 4 Triangle PQR has vertices as P(2, 4), Q(4, 6) and R(2, 6). It is Desired to reflect through an
arbitrary line L whose equation is y = 0.5 X + 2. Calculate the new vertices of triangle and show
the results graphically.
ΔPQR =
2 4 1
4 6 1
2 6 1
Reflection about y = 0.5 X +2
ty = -2,
m = slope =tan Ɵ
Ɵ = 26.565°
ΔP’Q’R’ = ΔPQR · T · R · M · (inv R) · (inv T)
ANS =
2.8 2.4 1
5.6 2.8 1
4.4 1.2 1

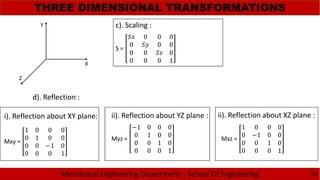
23. Mechanical Engineering Department – School Of Engineering
THREE DIMENSIONAL TRANSFORMATIONS
23
X
Z
Y
a). Translation :
[x’ y’ z’ 1] = [x y z 1] ·
1 0 0 0
0 1 0 0
0 0 1 0
1
b). Rotation :
Rz =
Ɵ Ɵ 0 0
− Ɵ Ɵ 0 0
0 0 1 0
0 0 0 1
i). Rotation about Z axis: ii). Rotation about X axis :
Rx =
1 0 0 0
0 Ɵ Ɵ 0
0 − Ɵ Ɵ 0
0 0 0 1
ii). Rotation about Y axis :
Ry =
Ɵ 0 − Ɵ 0
0 1 0 0
Ɵ 0 Ɵ 0
0 0 0 1

24. Mechanical Engineering Department – School Of Engineering
THREE DIMENSIONAL TRANSFORMATIONS
24
c). Scaling :
S =
0 0 0
0 0 0
0 0 0
0 0 0 1
d). Reflection :
Mxy =
1 0 0 0
0 1 0 0
0 0 −1 0
0 0 0 1
i). Reflection about XY plane: ii). Reflection about YZ plane :
Myz =
−1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
ii). Reflection about XZ plane :
Mxz =
1 0 0 0
0 −1 0 0
0 0 1 0
0 0 0 1
X
Y
Z

25. Mechanical Engineering Department – School Of Engineering
Example
25
Ex 5. State the homogeneous transformation matrices for the following operations.
a) Rotation through 120° about origin.
b) Translation through 10 and -20 units along the x and y direction respectively.
c) Rotation through 30° about origin.
Find concatenated matrix if the operations are done in above sequence. Will the order
in which the operations are done affect the end result?

26. Mechanical Engineering Department – School Of Engineering
Example
26
Ex 6. A triangle ABC having coordinates A (3, 4, -2) and B (-4, 6, 3), C (-6, 4, 3) is to be
rotated about X axis by 20° anticlockwise. Determine the new coordinates of the triangle.

27. Mechanical Engineering Department – School Of Engineering
Example
27
Ex 7. Given a point P (1, 3, -5), find :
a) Transformed point P’ if P is Translated by 2 unit in X 3 unit in Y and -4 unit in Z and
then rotated by 30° about the Z axis.
b). Same as in (a), but the point P is rotated first and then translated.
c). Is the final point P’ the same in both (a) and (b) ? Explain your answer.