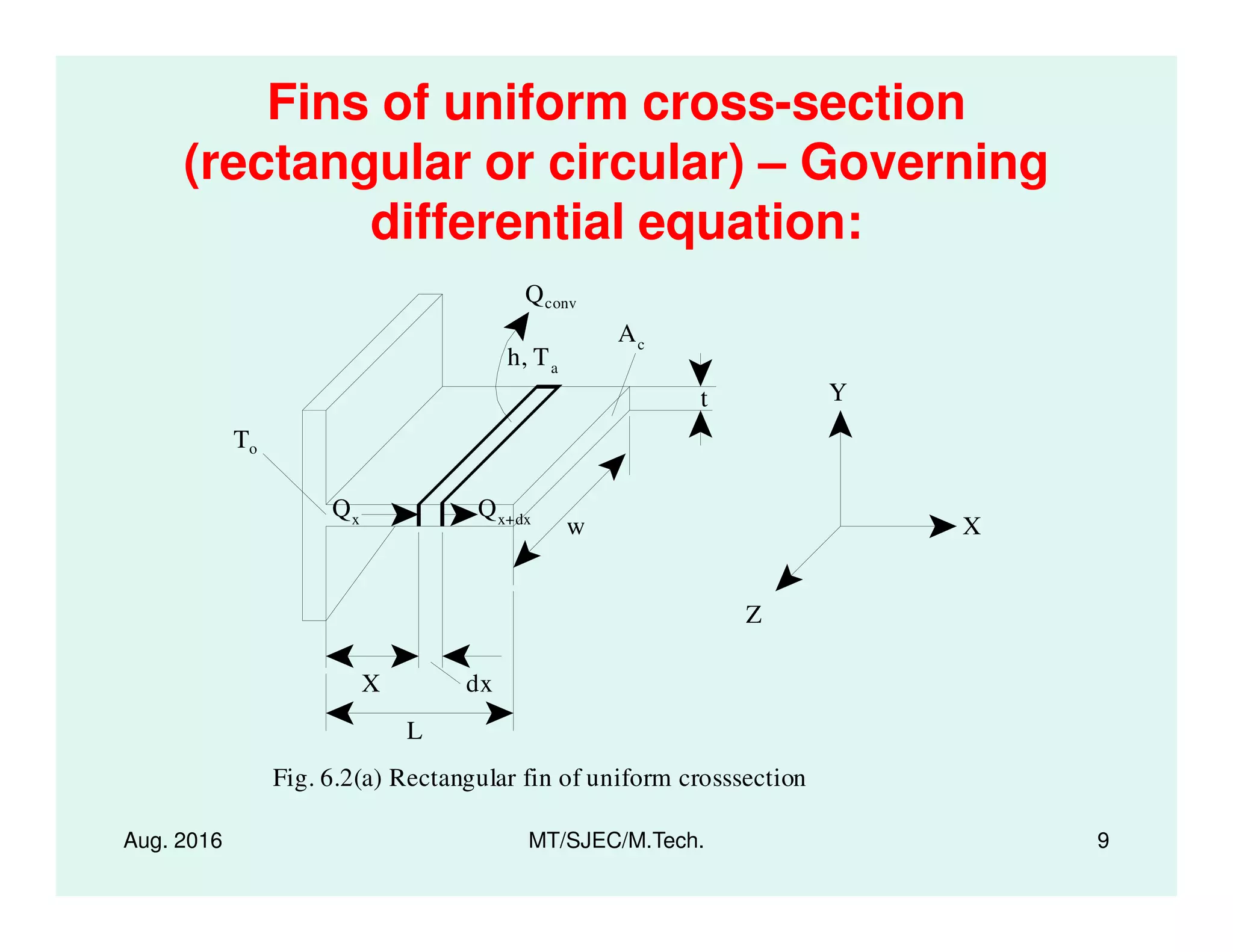
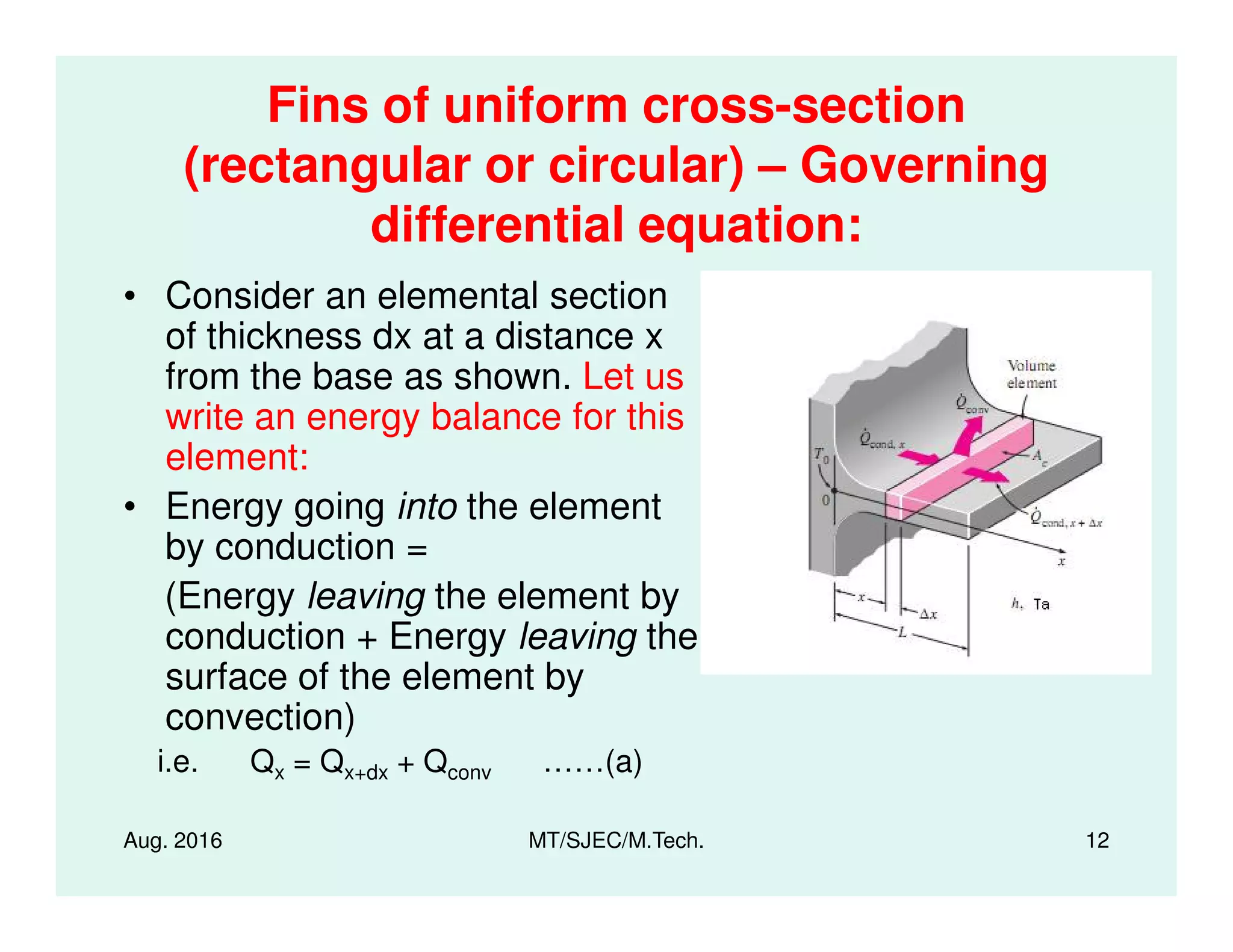
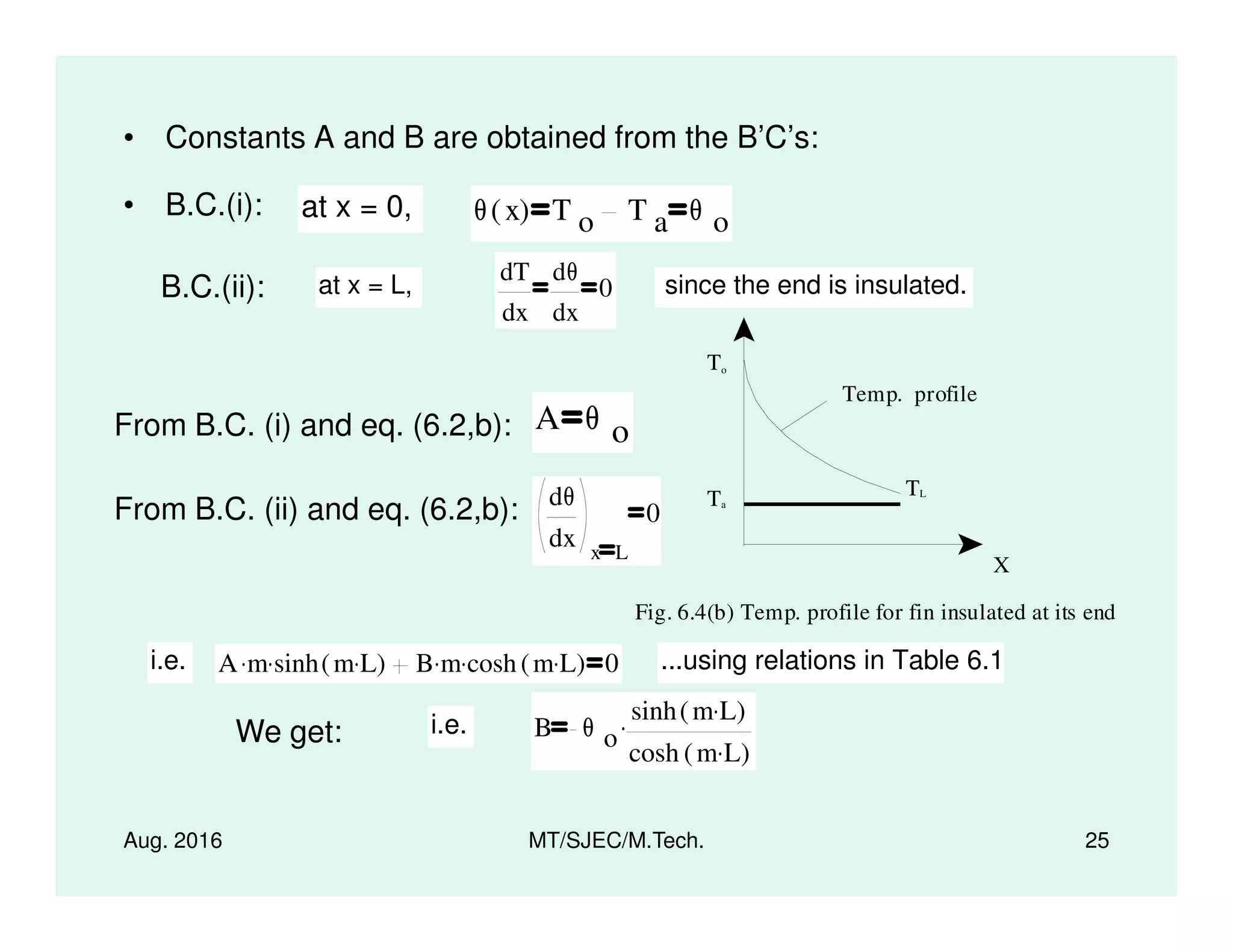
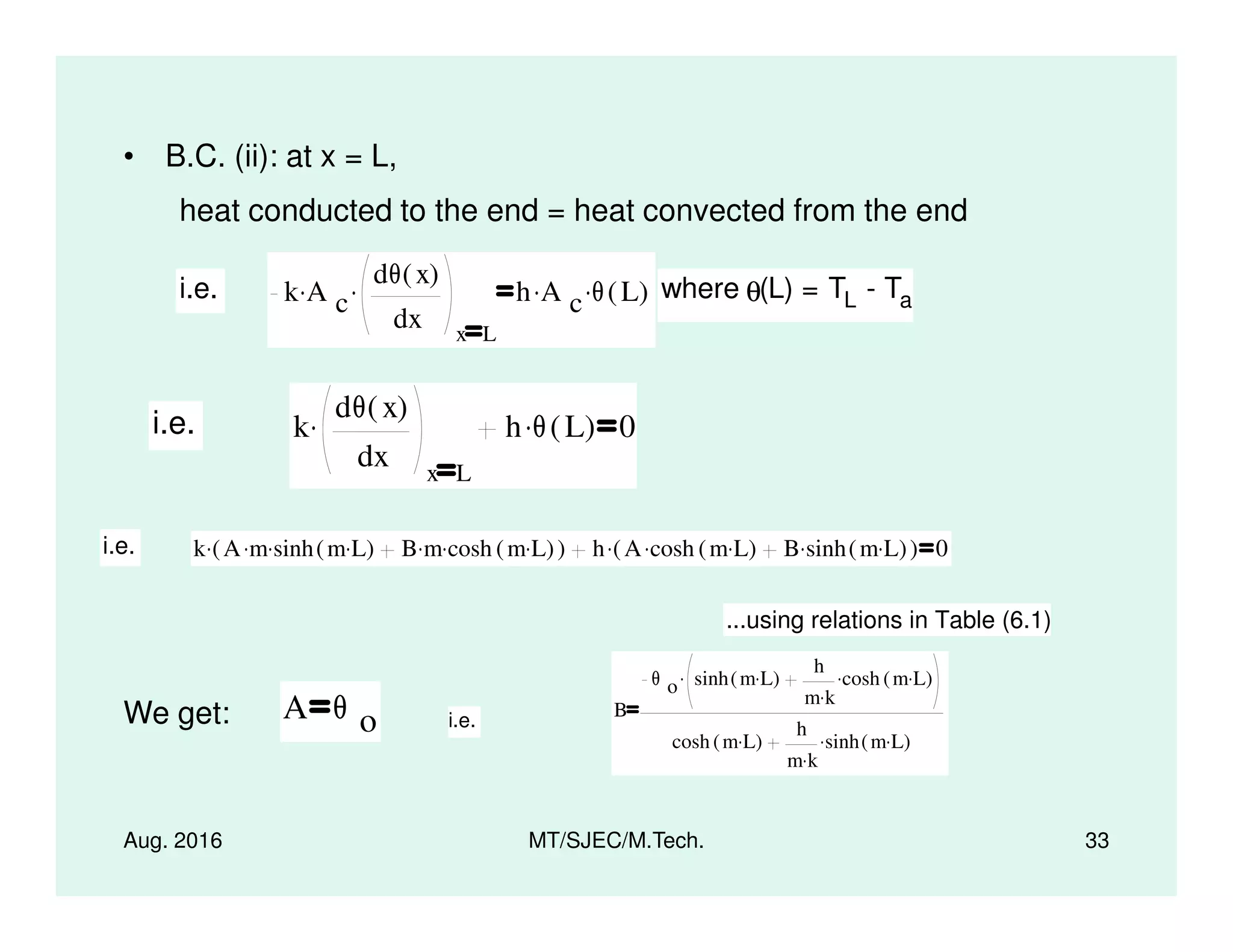
The document presents a series of lectures on heat transfer, focusing specifically on extended surfaces known as fins, developed by Dr. M. Thirumaleshwar for M.Tech. students. It covers key concepts, governing differential equations, and various performance metrics of fins, along with applications in several domains such as automotive and electronic cooling. Additionally, it includes methods for temperature distribution analysis and heat transfer calculations, as well as relevant references for further study.