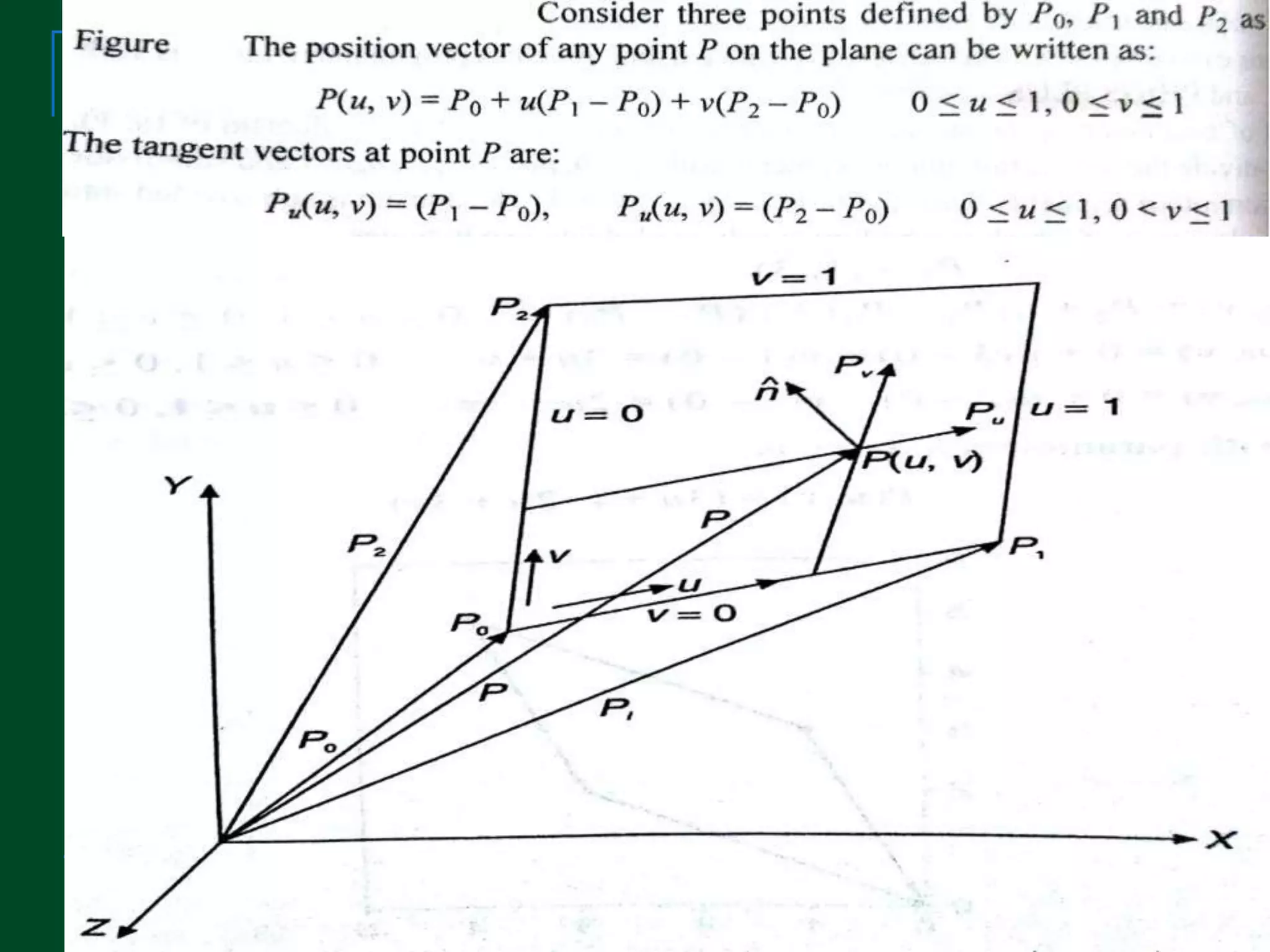
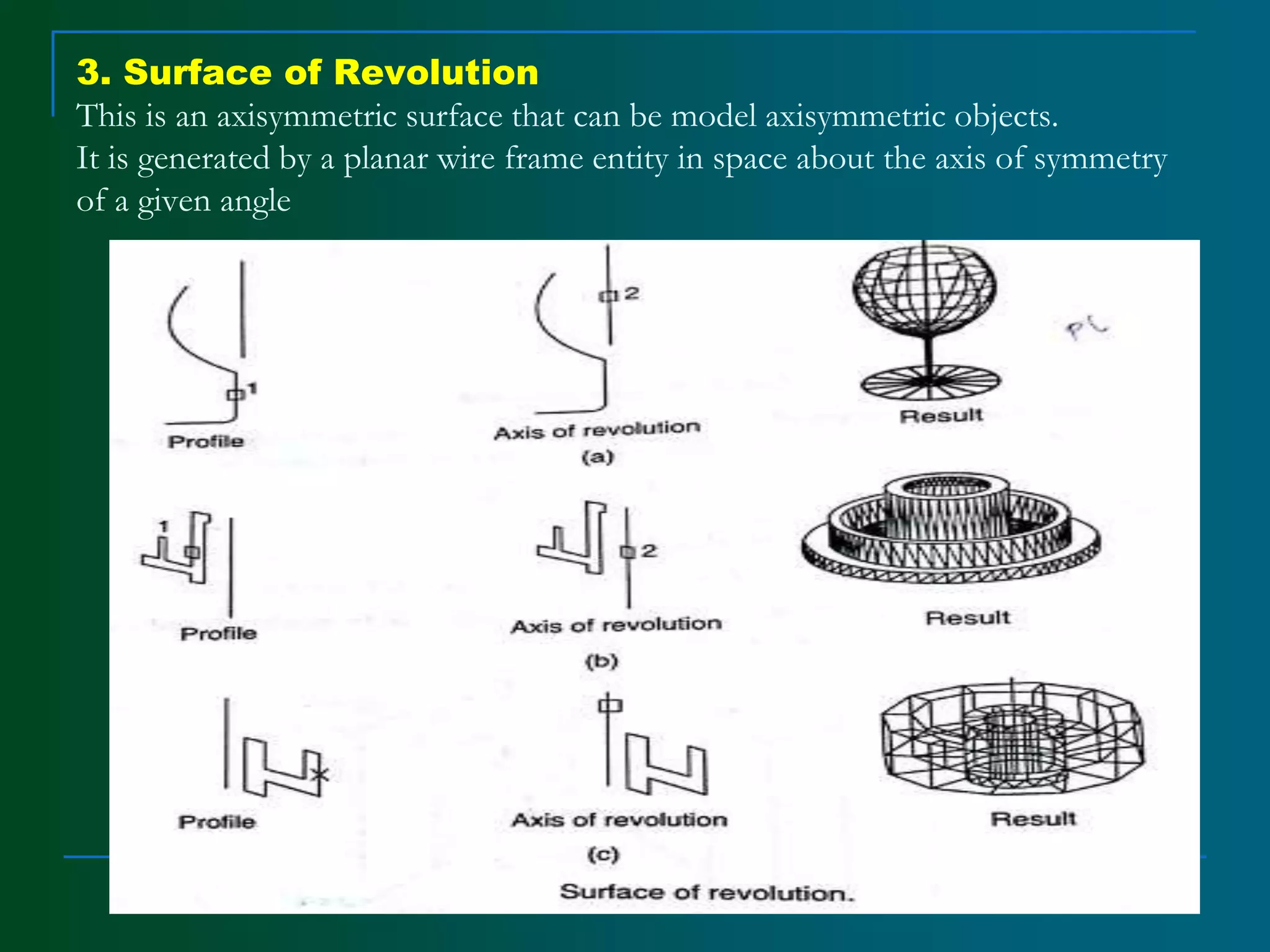
This document discusses different types of surface modelling techniques. Parametric surfaces and implicit surfaces are the two main types used in modelling systems. Parametric surfaces are defined by a set of coordinate functions, while implicit surfaces are defined by a polynomial equation. Common parametric surfaces include planes, ruled surfaces, surfaces of revolution, and B-splines. Multiple parametric surface patches can be joined to model more complex shapes. Surface modelling allows representing complex object geometries and is useful for mass properties calculation, interference detection, and finite element analysis.

1. Surface Modelling
Parametric Surfaces
■ Wire frame modelling are unable to represent complex surfaces
of objects like car , ship, airplane wing, castings but surface
model can used to represent the surface profile of these objects
■ surface model can be used for calculating mass properties ,
and interference between parts for generating view and finite
elements mesh and NC tool paths for continuous path
machining
■ This model used for fitting experimental data , discretised
solutions of differential equations, construction of pressure
surfaces , construction of stress distribution.
■ This surface of object is a more complete and less ambiguous
than the wire frame modeling

3. Surface Entities
■ 1.Analytic surfaces
plane , ruled surfaces , surface of
revolution and tabulated cylinder.
■ 2 Synthetic surfaces
Hermite bi- cubic surface , Bezier
surface and B – Spline surface

4. Surface Modeling
■ There are two types of surfaces that are
commonly used in modeling systems,
parametric and implicit.
■ Implicit Surface: It is defined by a polynomial
of three variables :f ( x ,y , z )=0
■ Example: (x-x0)2+(y-y0)2+(z-z0)2-r2=0
■ 8 X 2- X Y 2 + X Z 2 + Y 2 + Z 2 – 8 = 0
■ Surfaces which have polynomial (implicit)
forms are called algebraic surfaces

5. Parametric Surfaces
■ Parametric surfaces are defined by a set of three functions,
one for each coordinate
x=f(u,v), y=f(u,v), z=f(u,v)
■ Where u and v are in certain domain in the range of 0 and 1 .
■ Thus (u , v ) is a point in the square defined by (0,0)
(1,0) ,(0,1) and (1,1)in the uv – coordinate plane.

6. ■ Parametric surfaces :
f(u,v) = ( x(u,v), y(u,v), z(u,v) )
■ Assume both u and v are in the range of 0 and 1.

7. Parametric Surfaces
■ Parametric surfaces or more precisely parametric surface
patches are not used individually.
■ Many parametric surface patches are joined together side-by-
side to form a more complicated shape.
Patch

8. Parametric Surface Patch
■ Each patch is defined by control points net
(Control Polyhedron).

9. Parametric Surface Patch
■ A parametric surface patch can be considered as a union of
(infinite number) of curves.
■ Given a parametric surface f(u,v), if u is fixed to a value, and let v
vary, this generates a curve on the surface whose u coordinate is a
constant. This is the isoparametric curve in the v direction.
■ Similarly, fixing v to a value and letting u vary, we obtain an
isoparametric curve whose v direction is a constant.

10. Parametric Surface Patch
■ Point Q(u,v) on the patch is the tensor product
of parametric curves defined by the control
points.

11. Surface Patch
■ The effect of “lifting” one of he control points of
a patch.

12. Quadric surfaces in normal forms

17. Quadric surfaces in general form
■ It has ten co-efficients

18. Parametric representation of Analytic surfaces
p
1. Plane surface :
■ This is the simplest surface and requires three
non – coincidental points to define an infinite
plane
■ The plane surface can be used to generate cross –
sectional views by intersecting a surface with it.

21. 2. Ruled (lofted) surface: This is linear surface ,interpolates
linearly b/w two boundary curves that define the surface.
Boundary curves can be in the form of any wireframe entity

23. 3. Surface of Revolution
This is an axisymmetric surface that can be model axisymmetric objects.
It is generated by a planar wire frame entity in space about the axis of symmetry
of a given angle

24. Line AB is rotated abt the z- axis through an angle of 1800 generating
cylinder.
Any point on the surface is a function of two parameters U and ɵ
u describes the entity to be rotated and ɵ represent the angle of
rotation .In general form
P(u , v)= r (u) cos ɵ + r(u) sin ɵ + z(u ) n3

25. •4.Tabulated cylinder:
1.This is surface by translating a plane curve at a given distance
along a specified direction.
2.Plane of the curve is perpendicular to the axis of generated cylinder