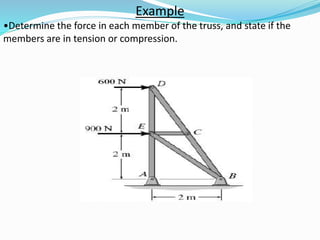
Trusses are structures composed of straight members connected at joints. They have three key characteristics: they only experience axial loads, loads are applied only at end points, and members are joined by pins. Trusses are used to support roofs and bridges. To analyze a truss, assumptions are made that loads act only at end points, member weight is ignored, and members experience only axial loads as either tension or compression. The method of joints and method of sections can be used to calculate the internal forces in each member and determine if each member is in tension or compression.

1. Trusses

2. What are Trusses?
In architecture and structural engineering, a truss
is a structure comprising one or more triangular units
constructed with straight members whose ends are
connected at joints referred to as nodes. External
forces and reactions to those forces are considered to
act only at the nodes and result in forces in the
members which are either tensile or compressive
forces. Moments (torques) are explicitly excluded
because, and only because, all the joints in a truss are
treated as revolutes (revolute joint).

3. Shortly, a truss has the following
three characteristics:
1-Axial loads only.
2-Loads are applied at end points
only.
3-Elements are joined by pins only.

4. See some pictures of trusses:

6. Planar trusses: planar trusses lie in a
single plane and are often used to
support roofs and bridges.
In roof trusses, the roof load is
transmitted to the truss at the joints by
means of a series of purlins.

7. Assumptions for design:
To design both the members and the connections of a
truss, it is first necessary to determine the force
developed in each member when the truss is
subjected to a given loading. In this regard, these
assumptions will be made:
1- Loads are applied at end points only.
2- Weight of the elements is neglected.
3- Elements are joined by pins only.
4- Axial loads only: if the force tends to elongate the
member, it is a tensile force; whereas if it tends to
shorten the member, it is a compressive force.

8. Truss problems
Some important notes:
•When a force (F) is applied at the center of a
member of the truss, it must be divided into two
equal forces (F1 & F2) where: F1= F2= F/2 and F1& F2
are applied at the ends of the member as shown in
the following figure:

9. •When a force (F) is applied along the member but
not at the center, it is divided as follows:

10. •We will assume all the internal forces to be in
tension then after solving the problem, the
positive forces are tension and the minus forces
are compression.
•It is required to calculate the internal forces in
each member of the truss and state if the
members are in tension or compression using
two methods:
•Joints or nodes method. b) Sections
method.

11. Special cases:
•Zero force members:
When you look to the truss you can determine them as follows:
•Four members each pair are on the same straight line:
The previous two special cases can be proved by applying equilibrium on the forces.

12. How to solve truss problems:
•Draw the free body diagram.
•Calculate the external forces and support reactions.
•For the method of nodes:
•Choose a node whose number of unknown forces
doesn’t exceed two then study its equilibrium using
static equilibrium equations to determine these
forces: ∑Fx=0 & ∑Fy=0 & ∑M=0
•Go to the next node and study its equilibrium using
the evaluated forces from the previous node then go
to the next node and so on.

13. •For the method of sections:
•Take an imaginary section to cut the truss into two
pieces in condition that the number of unknown
forces doesn’t exceed three.
•Apply equilibrium equations on one piece of the
truss
∑Fx=0 & ∑Fy=0 & ∑M=0
•After determining all the forces, the positive forces
are tension and the minus forces are compression.

14. Example
•Determine the force in each member of the truss, and state if the
members are in tension or compression.

15. solution

16. First, we should calculate reactions at A and B:
∑MA =0
(By ) (2) + (900) (2) + (600) (4) = 0
... By = -2100 N = 2100N
∑Fy =0
Ay - By = 0 Ay = By
Ay = -2100N = 2100 N
∑Fx = 0
Ax – Bx + 900+ 600 = 0 Ax – Bx = -1500 ---------- (1)

17. Node A:
Ax = 0
F1 = 2100 N (Tension)
By substituting in eqn 1, we get:
Bx =1500 N
Node D:
F6 + 600 = 0 F6 = -1341.6 N
F6 = 1341.6 N (compression)
F2 - (1341.6) = 0
F2 = 1200 N (Tension)

18. Node c:
CE is a zero force member, so F3 = 0 and F6 = F5 = 1341.6 N (compression)
Node E:
F4 sin45 = -900
F4 = -1272.8 N = 1272.8 (compression)

19. References :
1/ Engineering mechanics statics by
R. C. HIBBELER
2/ Lecture notes annotated by
Dr . Mohamed tawfik
Cairo university
Assistant Professor
Giza, Al Jizah, Egypt