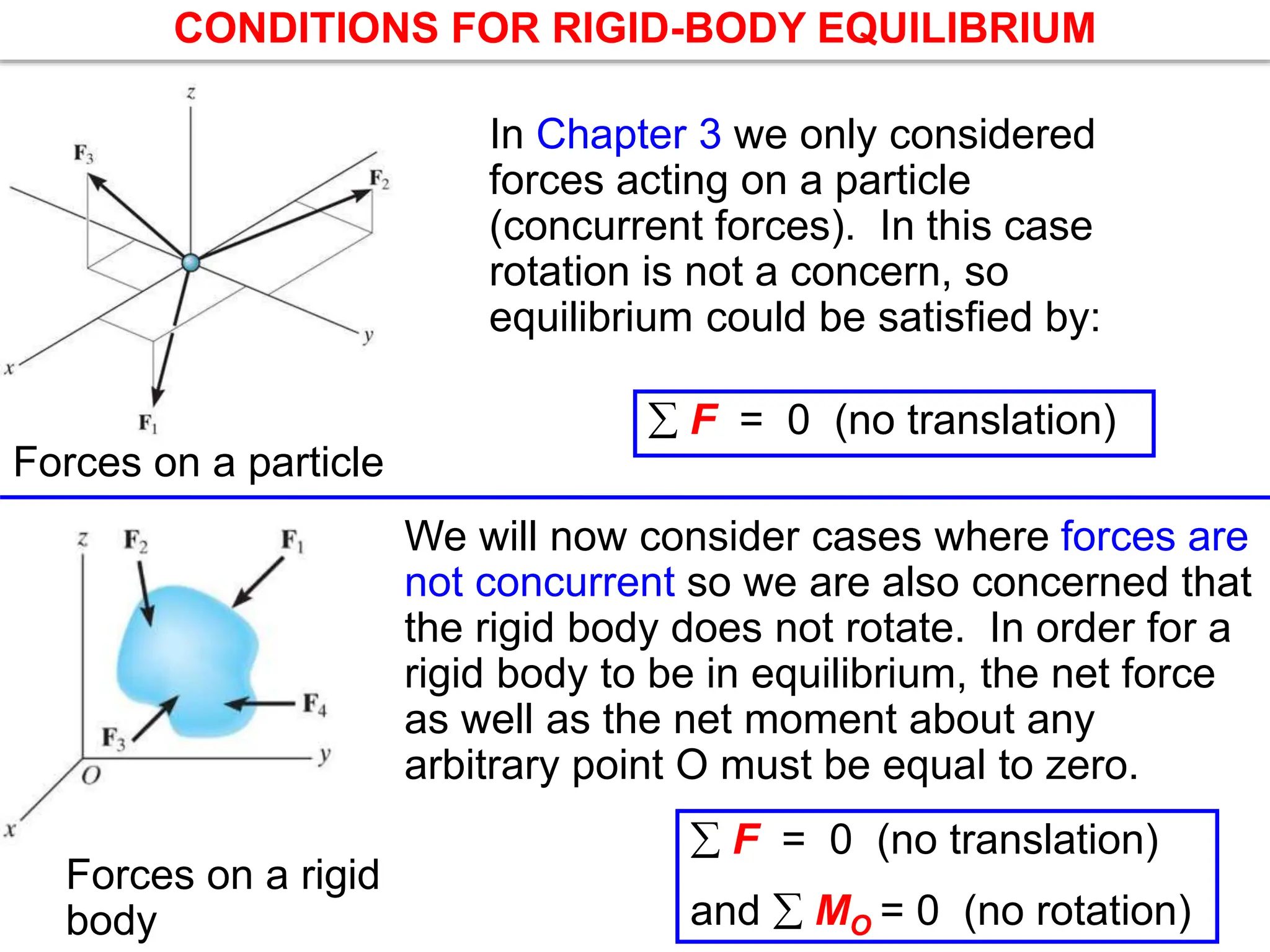
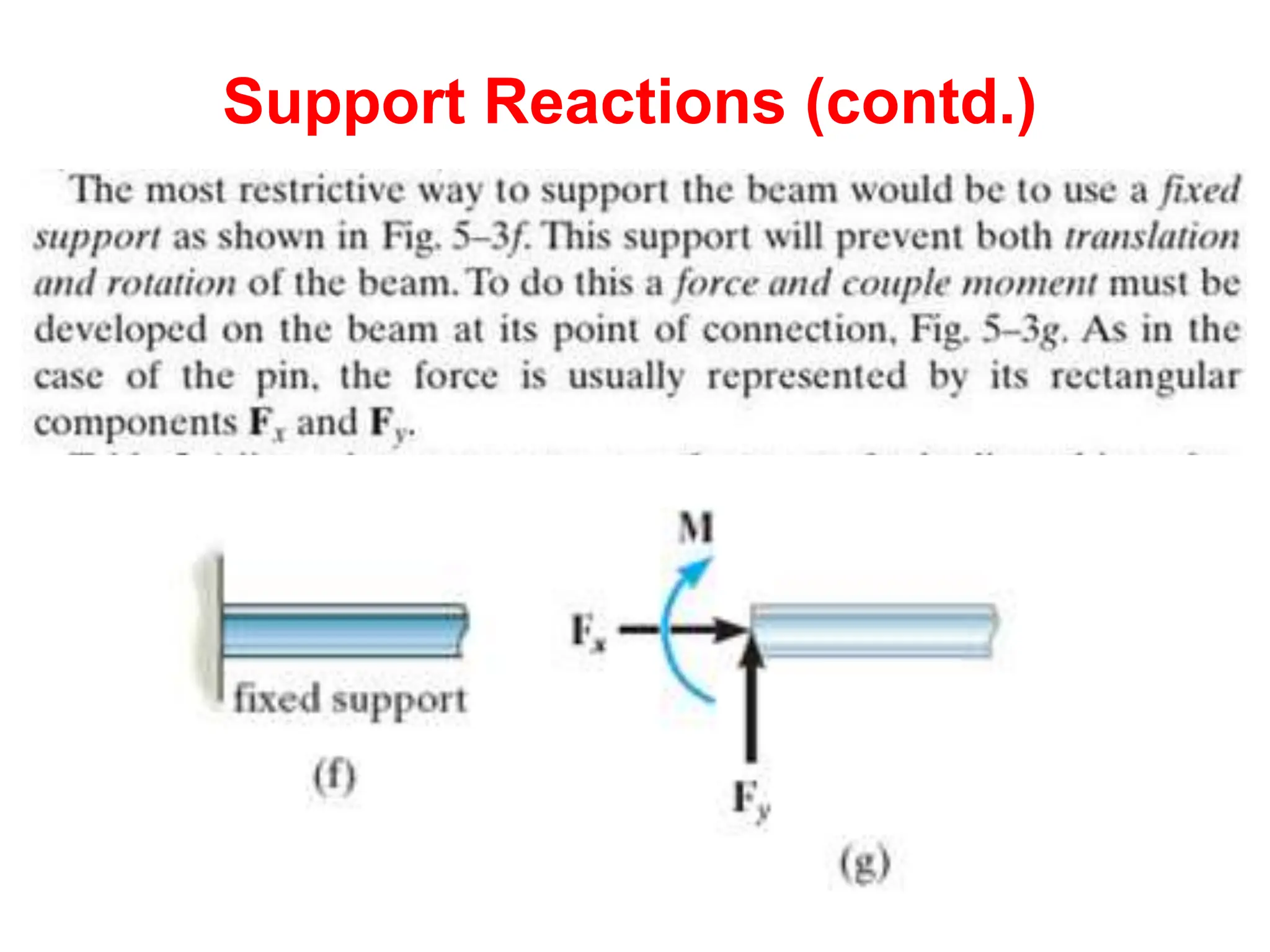
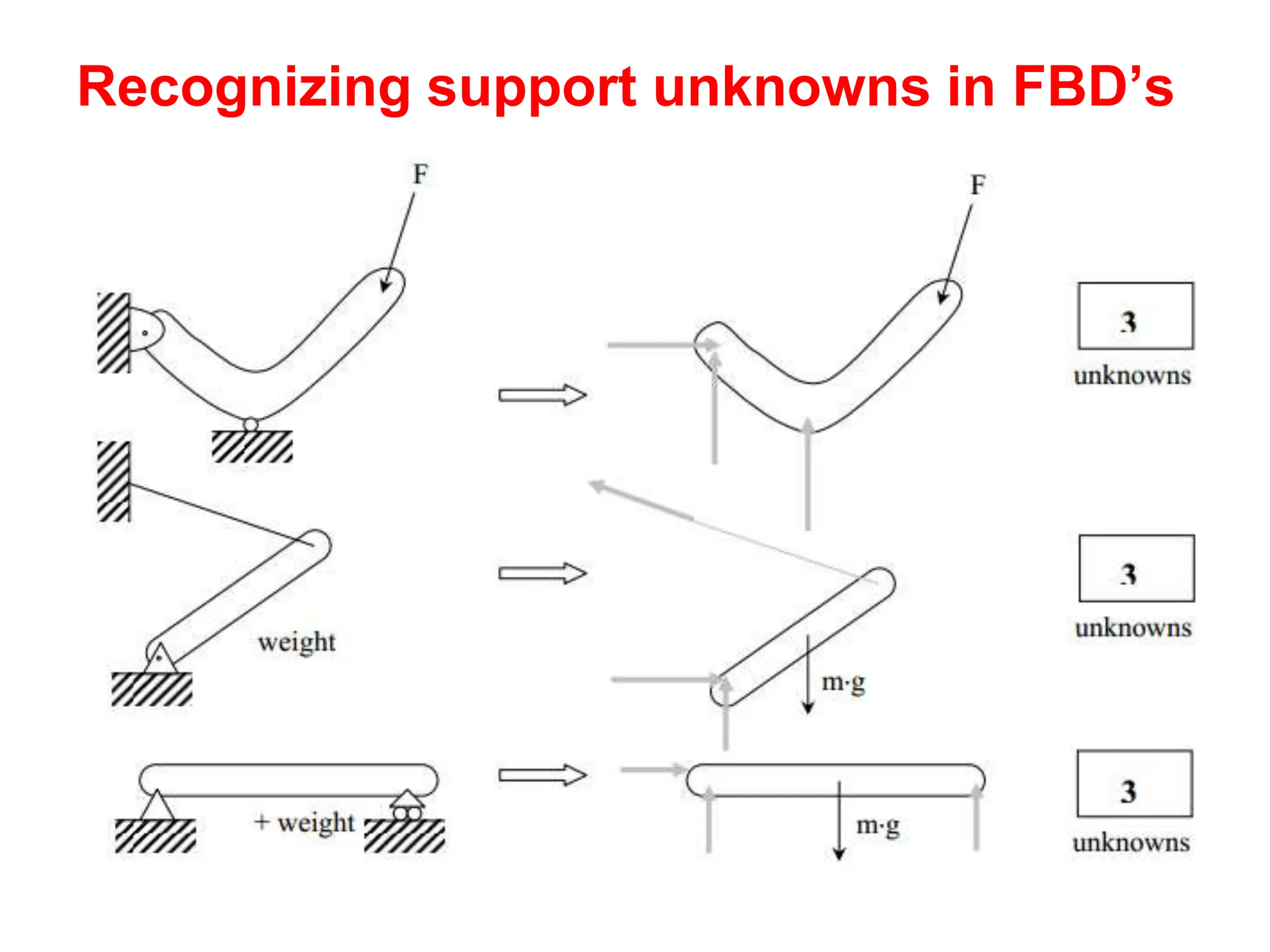
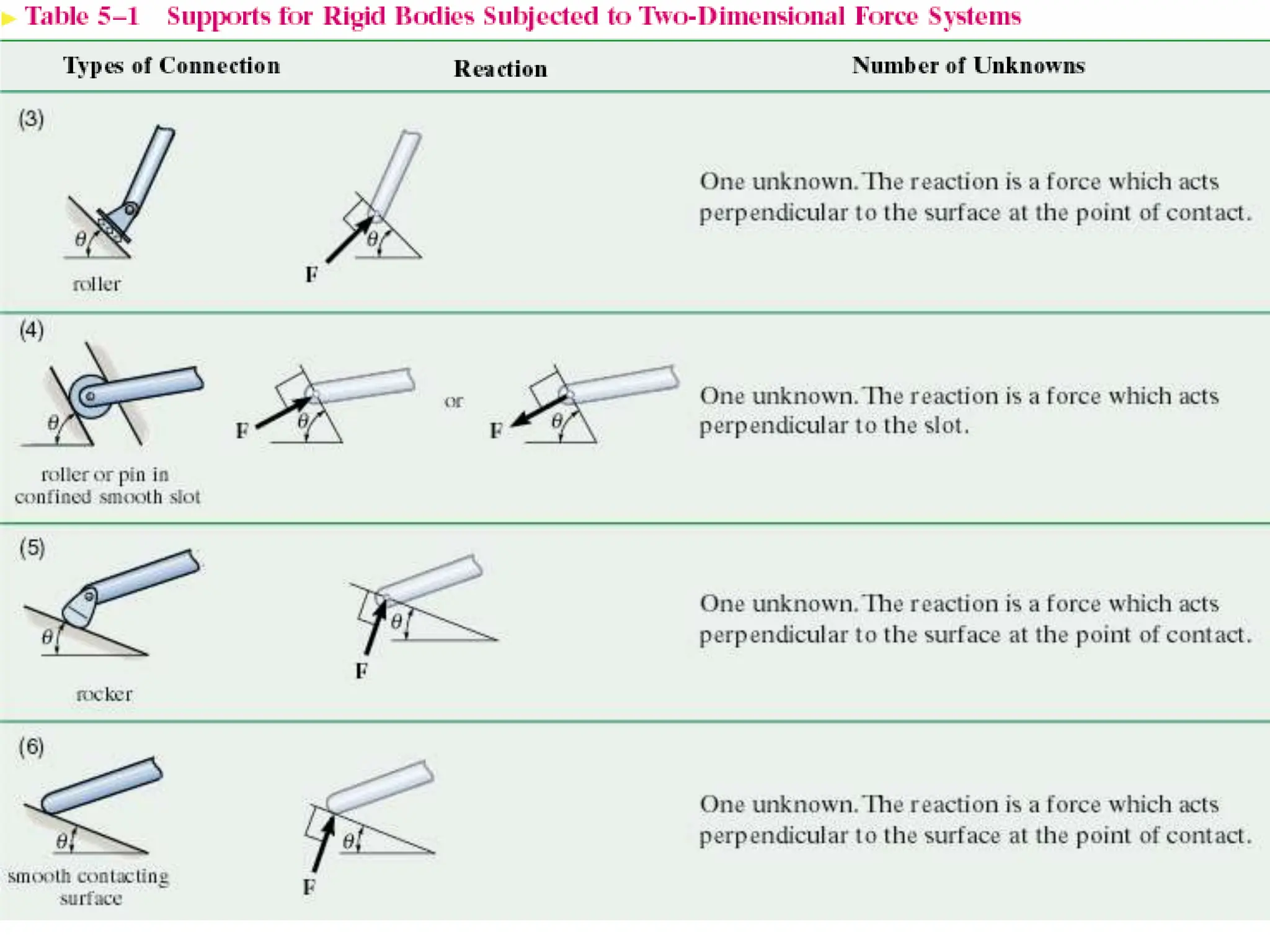
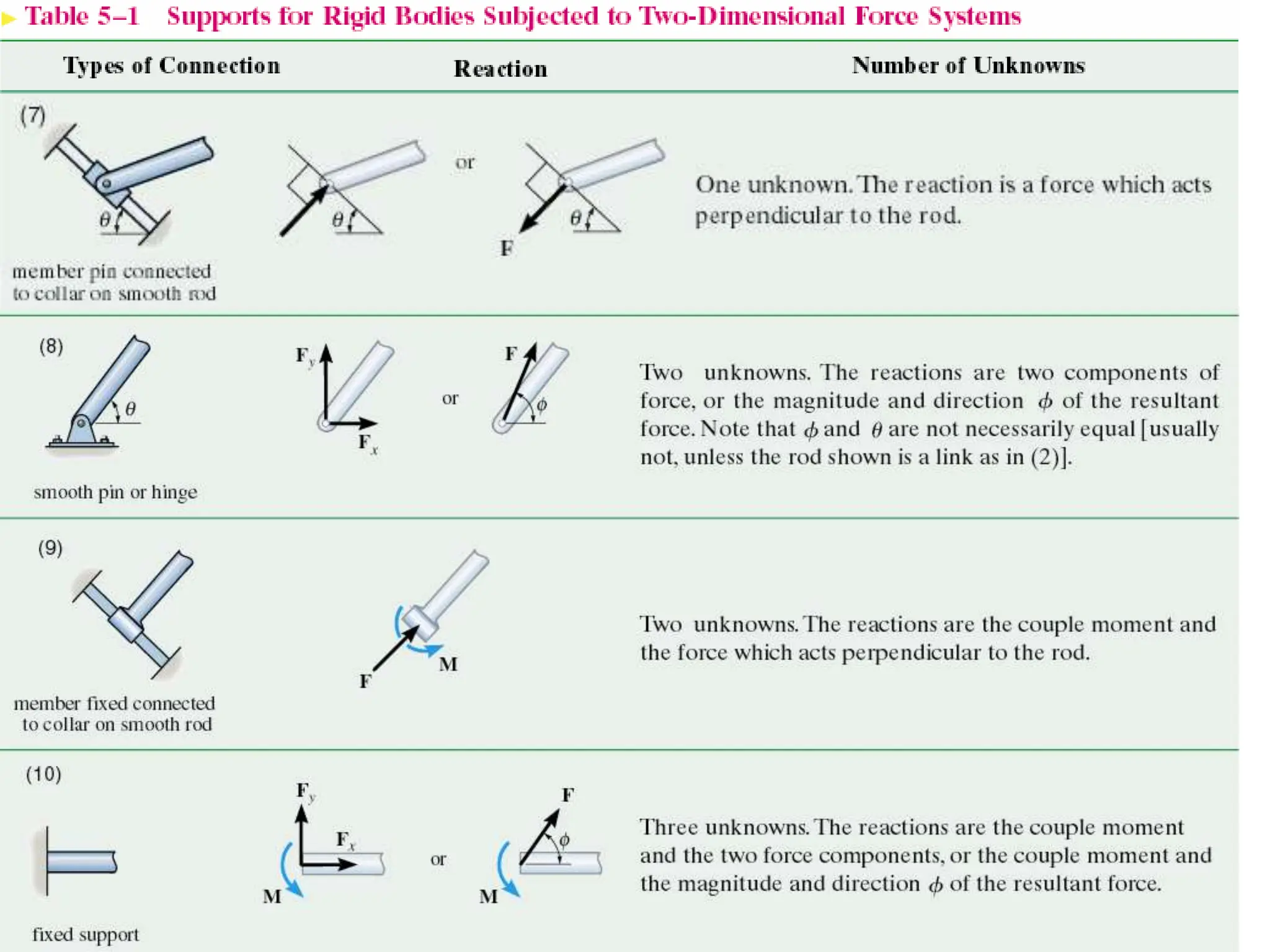
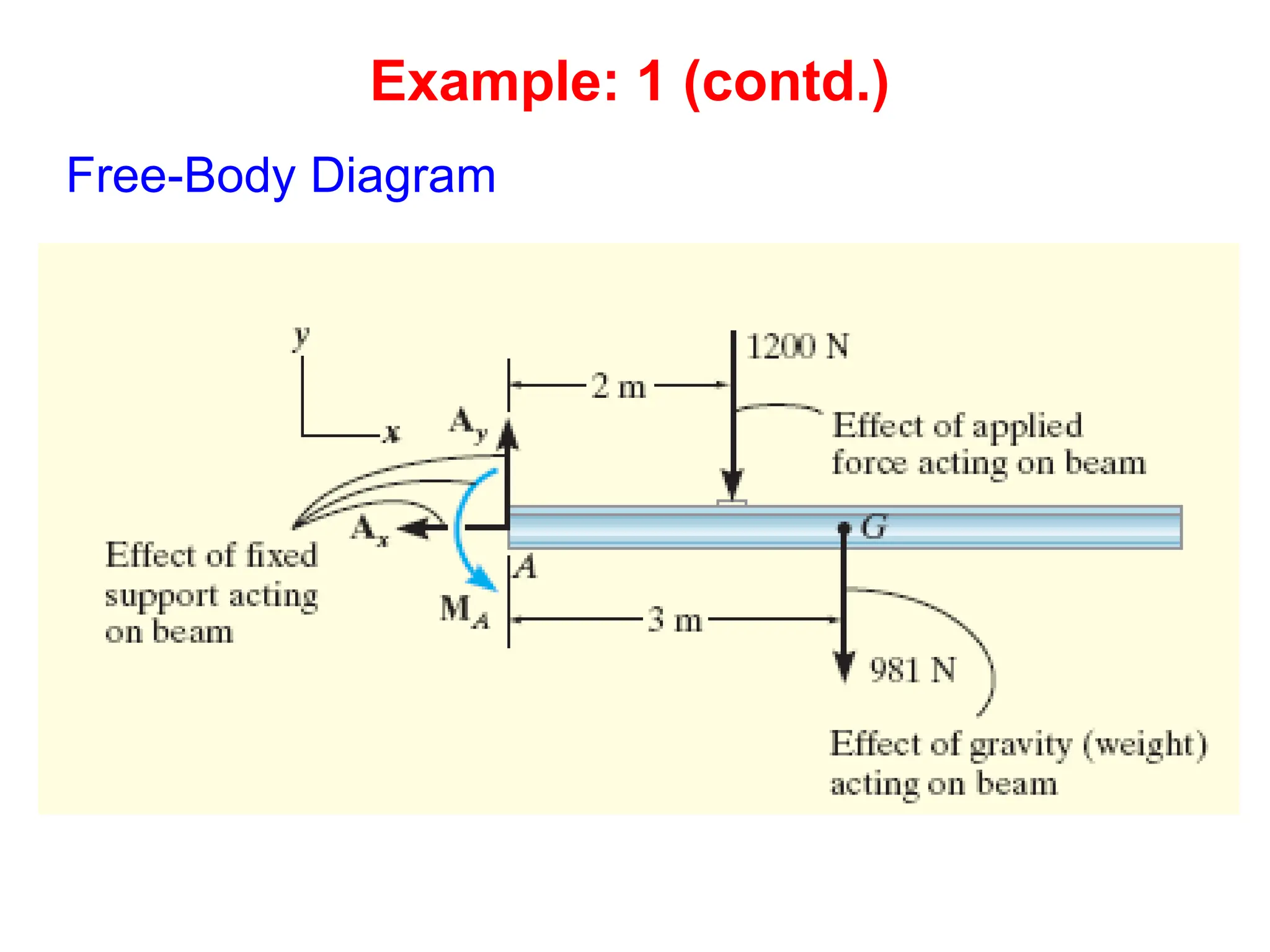
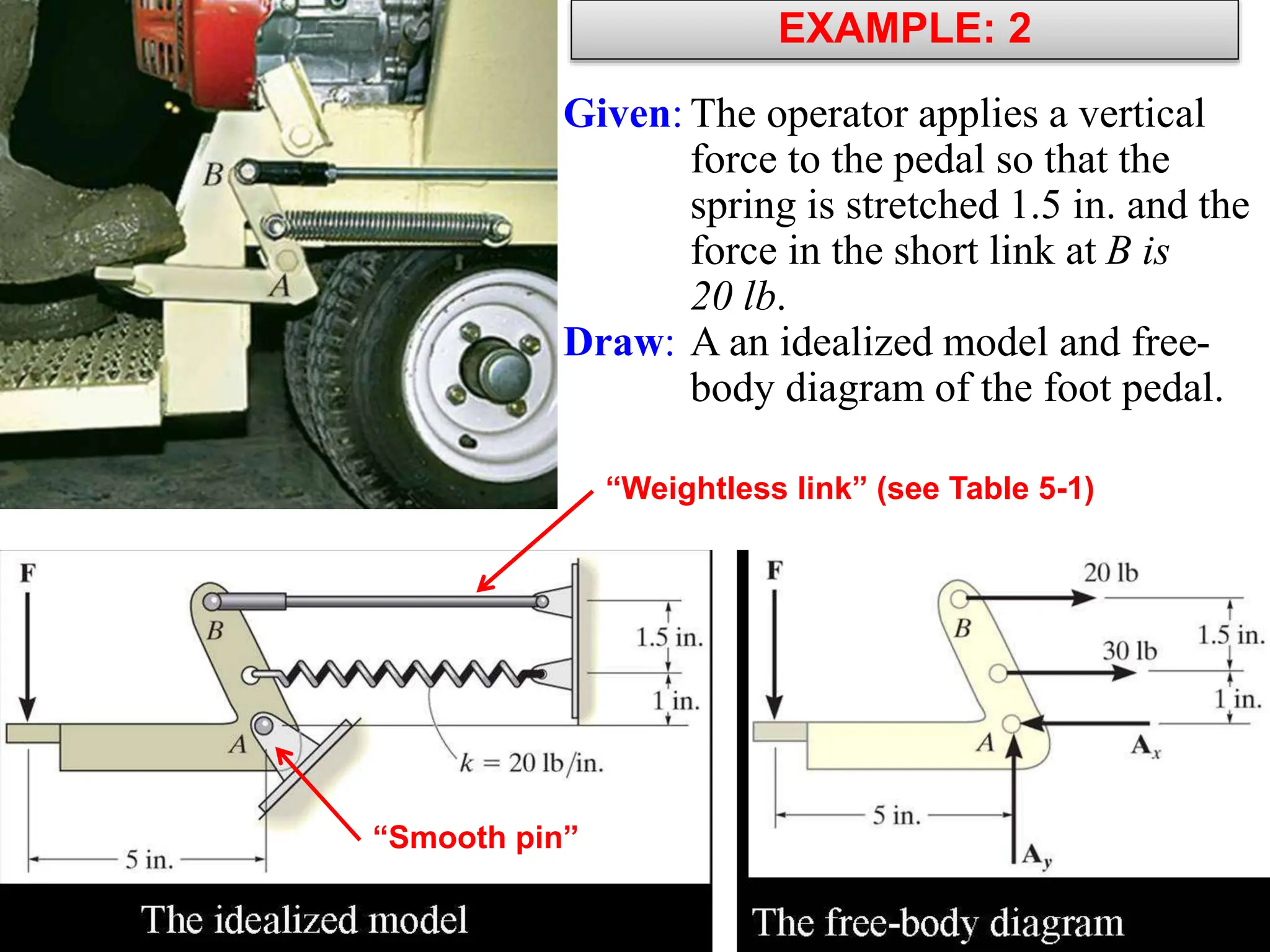
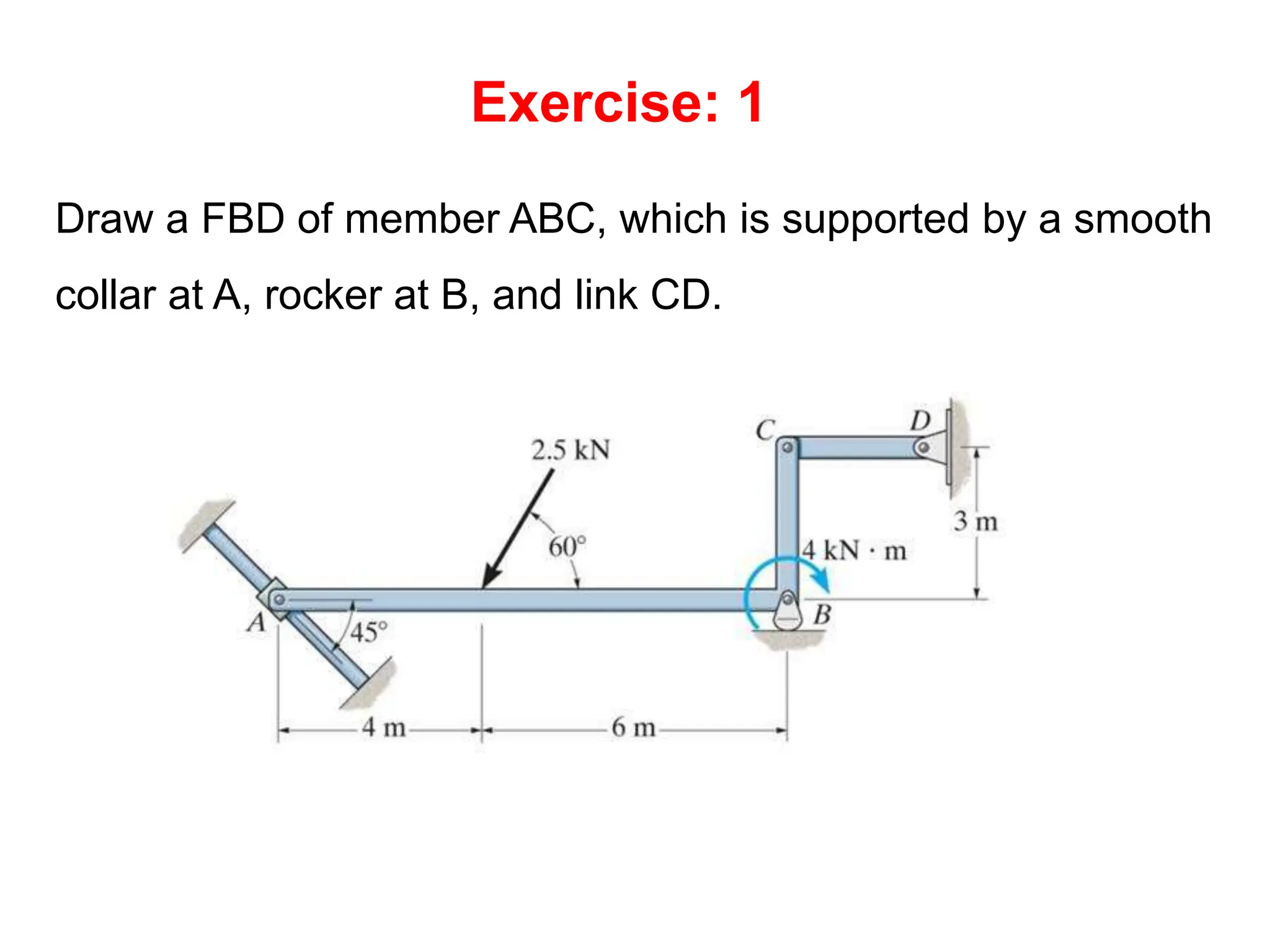
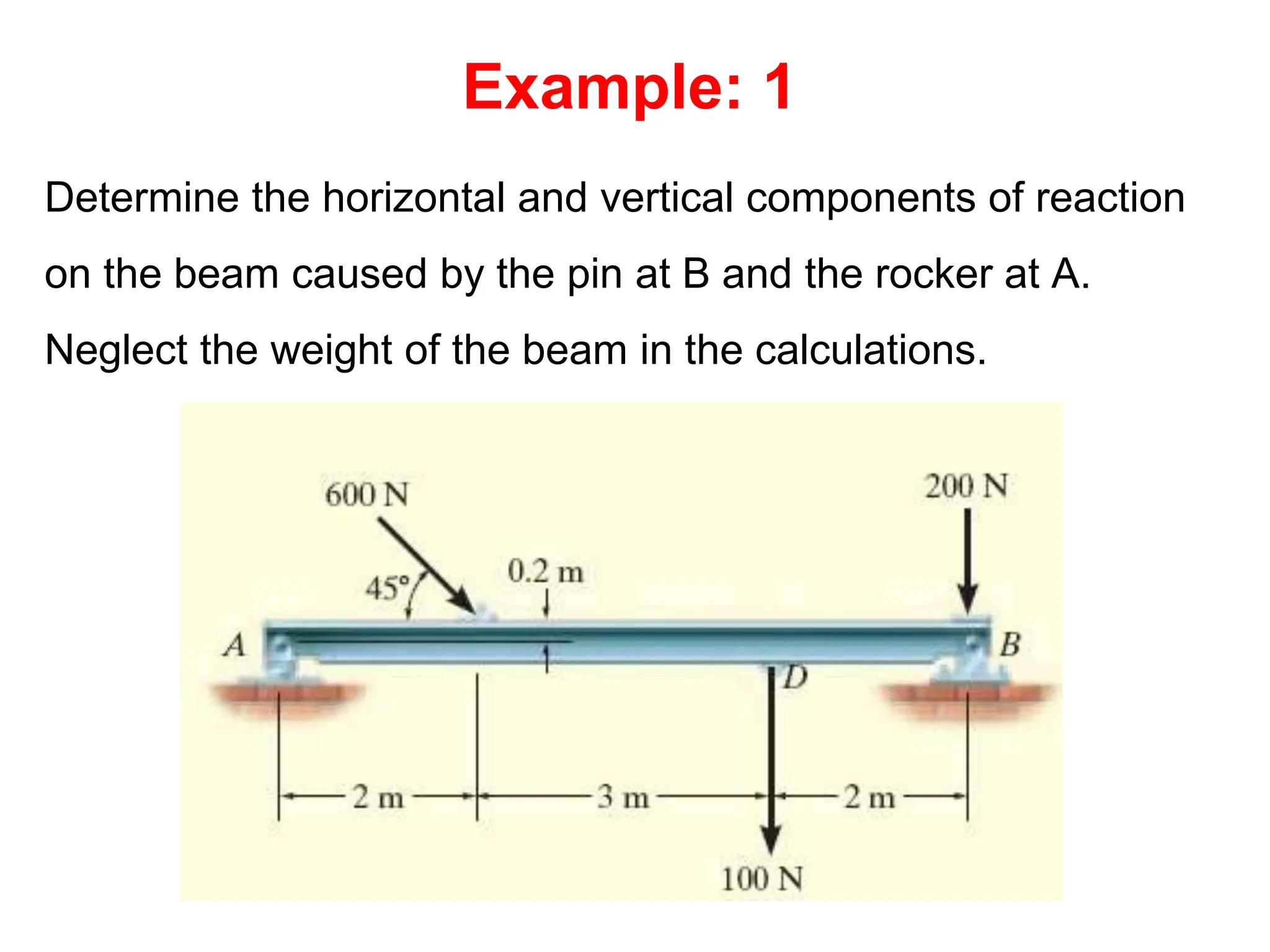
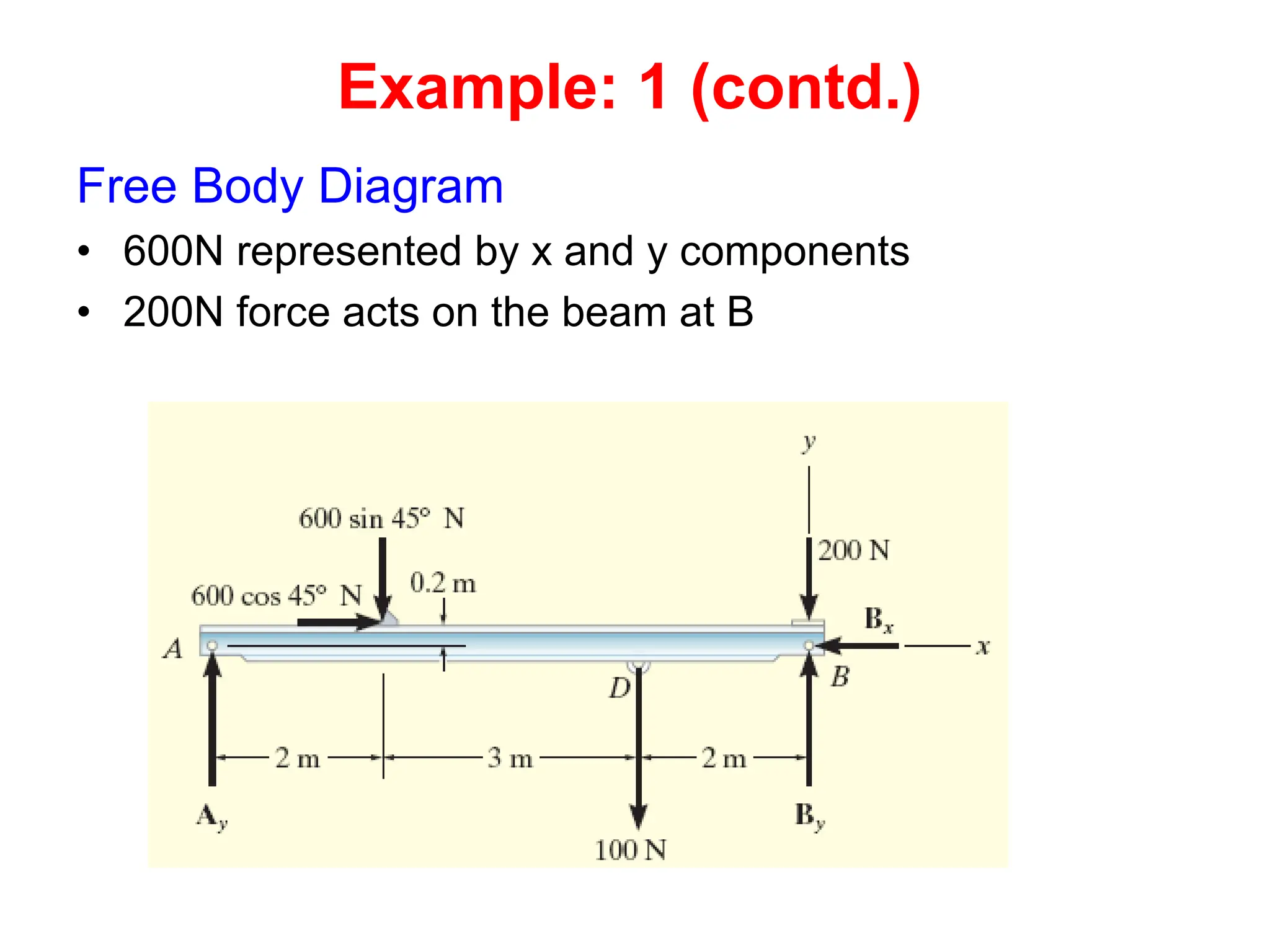
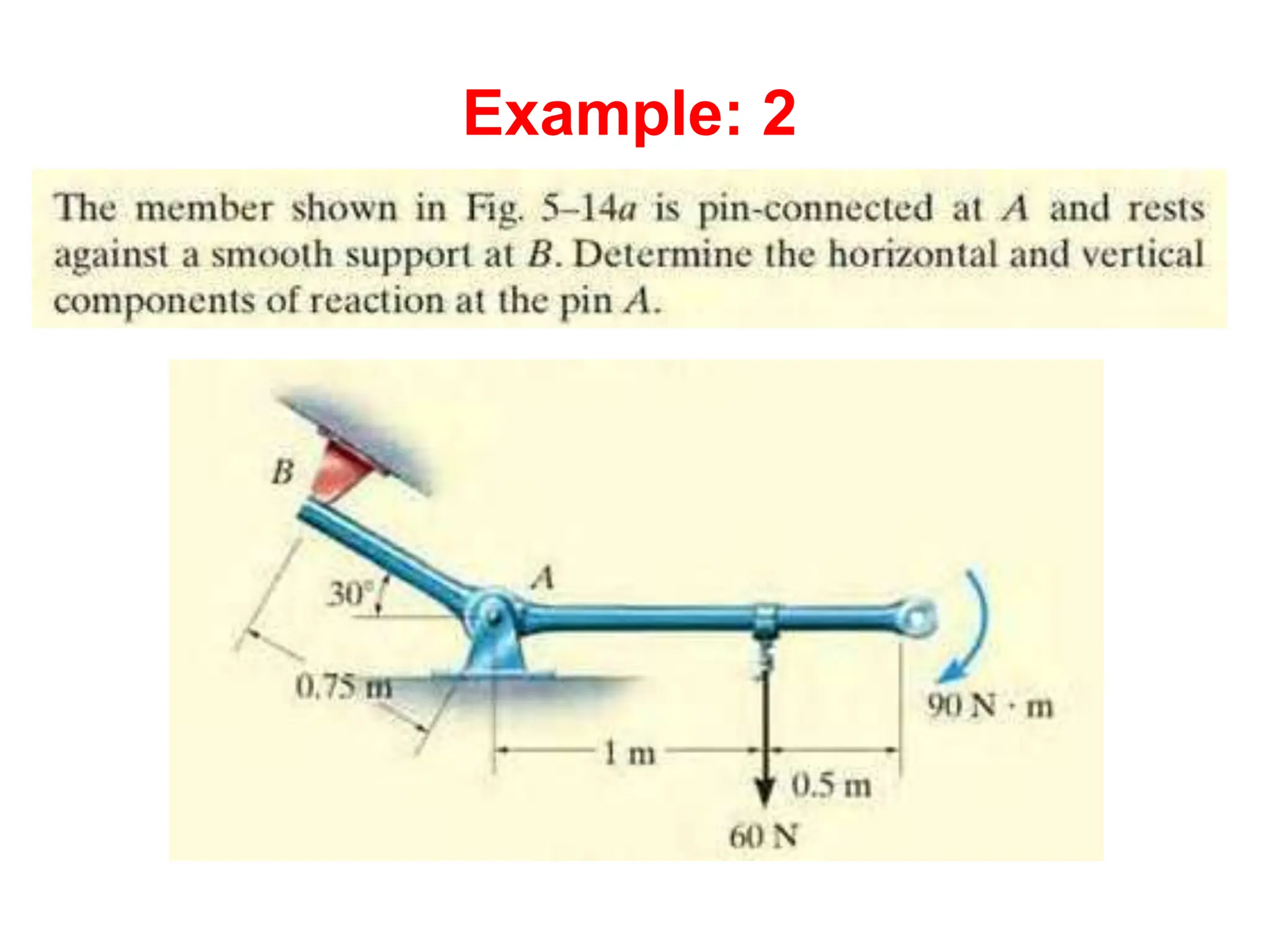
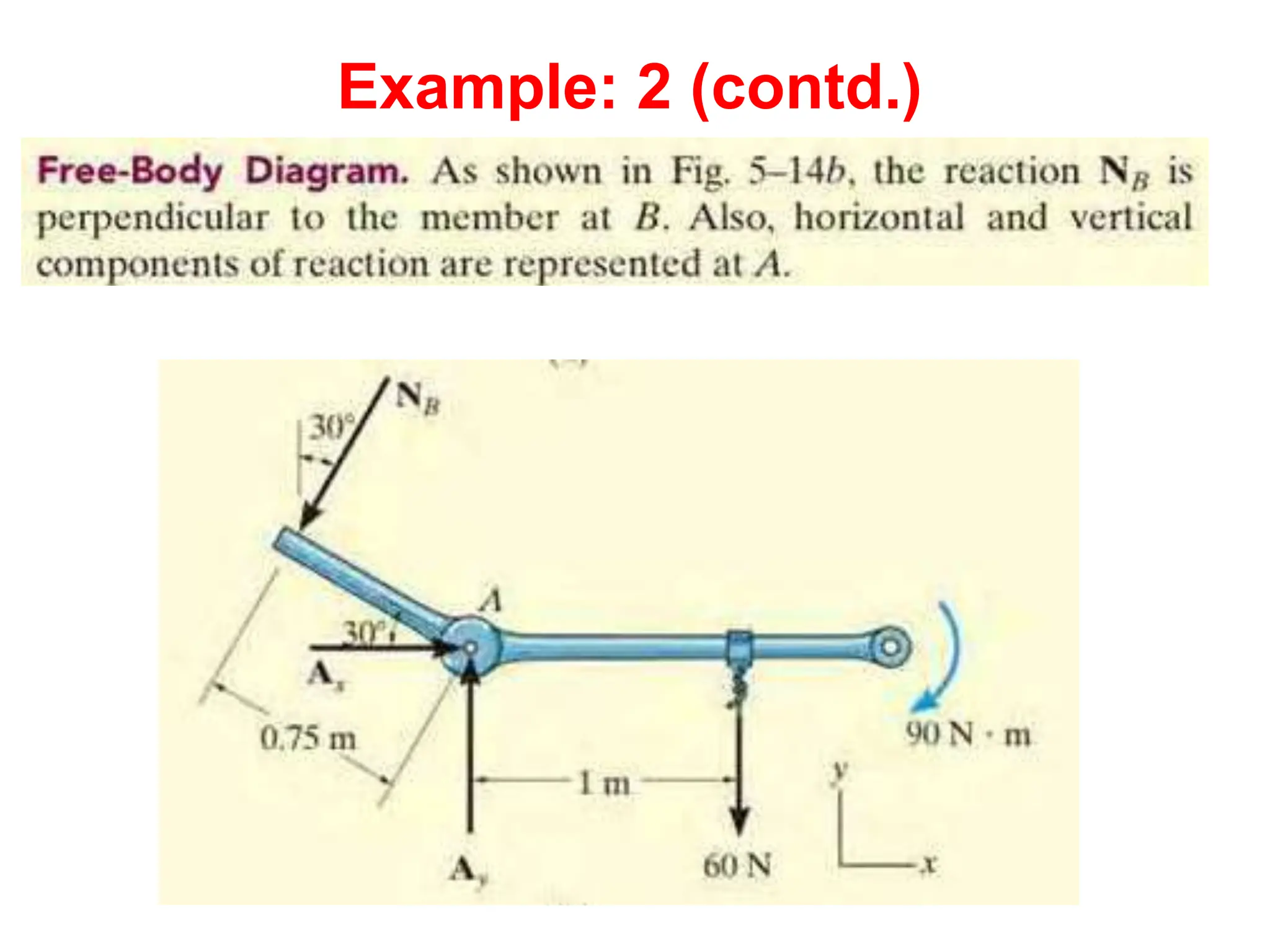
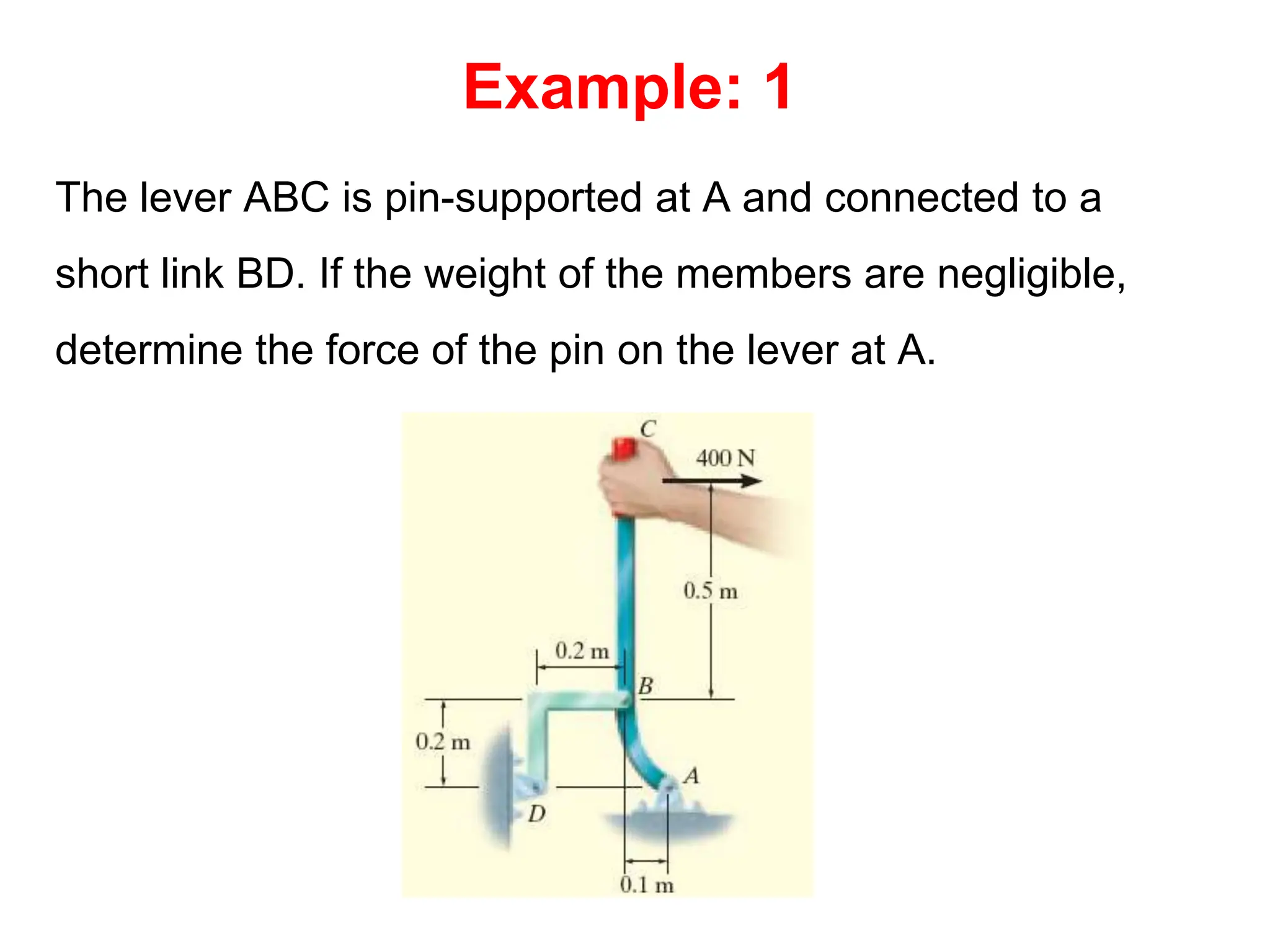
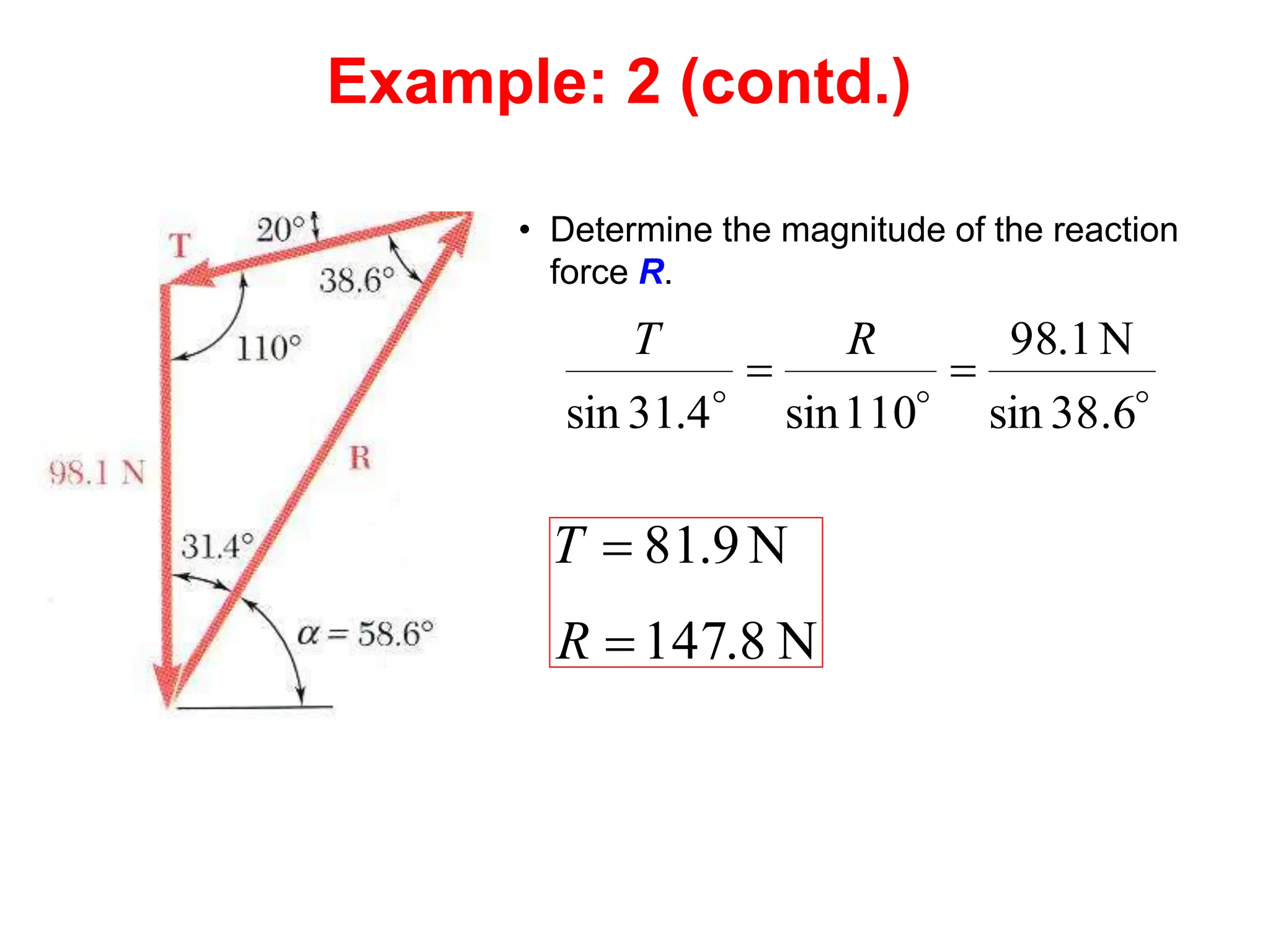
This document outlines the key concepts and objectives covered in the Engineering Statics course ME 1204. It discusses rigid bodies and the conditions required for rigid-body equilibrium. Namely, the net force and net moment about any point must equal zero. Free-body diagrams are introduced as a way to visualize all external forces and reactions acting on a body. The equations of equilibrium - the sum of forces in the x and y directions and the sum of moments about a point must equal zero - are provided to analyze rigid bodies in static equilibrium. Examples are given to demonstrate applying these concepts to solve equilibrium problems.

1. ME 1204: Engineering Statics
Dr. Faraz Junejo

2. Objectives
• Develop the equations of equilibrium for a rigid
body
• Concept of the free-body diagram for a rigid
body
• Solve rigid-body equilibrium problems using
the equations of equilibrium

3. Outline
1. Concept of Rigid Body
2. Conditions for Rigid Equilibrium
3. Free-Body Diagrams
4. Equations of Equilibrium

4. Rigid Body
 A rigid body can be considered as a combination of a
large number of particles in which all particles remain at
a fixed distance from one another, both before and after
applying a load.
 This model is important as material properties of any
body that is assumed to be rigid will not have to be
considered when studying the effects of forces acting on
the body.

5. Rigid Body (contd.)
 Statics deals primarily with the calculation of external
forces which act on rigid bodies in equilibrium.
 Determination of the internal deformations belongs to the
study of the mechanics of deformable bodies, which
normally follows statics in the curriculum i.e. Mechanics
or Strength of materials course.

6. CONDITIONS FOR RIGID-BODY EQUILIBRIUM
In Chapter 3 we only considered
forces acting on a particle
(concurrent forces). In this case
rotation is not a concern, so
equilibrium could be satisfied by:
Forces on a particle
We will now consider cases where forces are
not concurrent so we are also concerned that
the rigid body does not rotate. In order for a
rigid body to be in equilibrium, the net force
as well as the net moment about any
arbitrary point O must be equal to zero.
Forces on a rigid
body
 F = 0 (no translation)
and  MO = 0 (no rotation)
 F = 0 (no translation)

7. Conditions for Rigid-Body Equilibrium
• The equilibrium of a body is expressed as
  





0
0
O
O
R
R
M
M
F
F

8. Conditions for Rigid-Body Equilibrium
(contd.)
 Consider summing moments
about some other point, such
as point A, we require
 
 


 0
O
R
R
A M
F
r
M
  





0
0
O
O
R
R
M
M
F
F

9. Free Body Diagrams
Support Reactions
• If a support prevents the translation of a body
in a given direction, then a force is developed
on the body in that direction.
• If rotation is prevented, a couple moment is
exerted on the body.

10. Support Reactions (contd.)

11. Support Reactions (contd.)

12. Support Reactions (contd.)

13. Summary: Support Reactions
• A reaction is a force with known line of action, or a force
of unknown direction, or a moment.
• The line of action of the force or direction of the moment
is directly related to the motion that is prevented.

14. Recognizing support unknowns in FBD’s

15. Support Reactions in 2D (Table 5-1)
The 2D reactions shown below are the ones shown in Table 5-1 in
the text. As a general rule:
1) if a support prevents translation of a body in a given
direction, then a force is developed on the body in the opposite
direction.
2) if rotation is prevented, a couple moment is exerted on the
body in the opposite direction
memorize this table!

18. Free Body Diagrams (contd.)
Internal Forces
• External and internal forces can act on a rigid body
In summary:
• For FBD, internal forces act between adjacent particles which are
contained within the boundary of the FBD, are not represented
• Particles outside this boundary exert external forces on the
system

19. Internal Forces (contd.)

20. Free Body Diagrams (contd.)
Weight and Center of Gravity
• Each particle has a specified weight
• System can be represented by a single resultant force,
known as weight W of the body
• Location of the force application is known as the
center of gravity

21. Procedure for Drawing a FBD
1. Draw Outlined Shape
• Imagine body to be isolated or cut free from its
constraints
• Draw outline shape
2. Show All Forces and Couple Moments
• Identify all external forces and couple moments that
act on the body

22. 3. Identify Each Loading and Give Dimensions
• Indicate dimensions for calculation of forces
• Known forces and couple moments should be properly
labeled with their magnitudes and directions
Procedure for Drawing a FBD (contd.)

23. Example: 1
Draw the free-body diagram of the uniform beam. The
beam has a mass of 100kg.

24. Example: 1 (contd.)
Free-Body Diagram

25. Free-Body Diagram’s Description
• Support at A is a fixed wall, the wall exerts three reactions
on the beam. These three forces acting on the beam at A
denoted as Ax, Ay, Az, drawn in an arbitrary direction
• Unknown magnitudes of these vectors
• Assume sense of these vectors
• For uniform beam,
Weight, W = 100(9.81) = 981N
acting through beam’s center of gravity, 3m from A
Example: 1 (contd.)

26. EXAMPLE: 2
“Smooth pin”
“Weightless link” (see Table 5-1)
Given: The operator applies a vertical
force to the pedal so that the
spring is stretched 1.5 in. and the
force in the short link at B is
20 lb.
Draw: A an idealized model and free-
body diagram of the foot pedal.

27. Free-Body Diagram’s Description
Example: 2 (contd.)

28. Exercise: 1
Draw a FBD of member ABC, which is supported by a smooth
collar at A, rocker at B, and link CD.

29. Equations of Equilibrium
• For equilibrium of a rigid body in 2D,
∑Fx = 0; ∑Fy = 0; ∑MO = 0
• ∑Fx and ∑Fy represent sums of x and y components of
all the forces
• ∑MO represents the sum of the couple moments and
moments of the force components

30. Procedure for Analysis
Free-Body Diagram
• Force or couple moment having an unknown magnitude
but known line of action can be assumed
• Indicate the dimensions of the body necessary for
computing the moments of forces

31. Equations of Equilibrium
• Apply ∑MO = 0 about a point O, that lies at the
intersection of the lines of action of two unknown
forces.
• In this way, moments of these unknowns are zero
about O and a direct solution for the third unknown can
be obtained
Procedure for Analysis (contd.)

32. Equations of Equilibrium
• When applying the force equilibrium equations, orient
the x and y axes along the lines that will provide the
simplest resolution of the forces into their x and y
components
• Negative result implies scalar for a force or couple
moment magnitude is opposite to that was assumed on
the FBD
Procedure for Analysis (contd.)

33. Example: 1
Determine the horizontal and vertical components of reaction
on the beam caused by the pin at B and the rocker at A.
Neglect the weight of the beam in the calculations.

34. Free Body Diagram
• 600N represented by x and y components
• 200N force acts on the beam at B
Example: 1 (contd.)

35. Equations of Equilibrium
N
B
B
N
F x
x
x 424
0
45
cos
600
;
0 






 
N
B
B
N
N
N
N
F
N
A
m
A
m
N
m
N
m
N
M
y
y
y
y
y
B
405
0
200
100
45
sin
600
319
;
0
319
0
)
7
(
)
2
.
0
)(
45
cos
600
(
)
5
)(
45
sin
600
(
)
2
(
100
;
0




















Example: 1 (contd.)

36. Example: 2

37. Example: 2 (contd.)

38. Example: 2 (contd.)

39. Two- Force Members
• When a member is subject to no couple moments and
forces are applied at only two points on a member, the
member is called a two-force member.
• Only force magnitude must be determined

40. Two- Force Members (contd.)

41. EXAMPLE OF TWO-FORCE MEMBERS
In the cases above, members AB can be considered as two-
force members, provided that their weight is neglected.
This fact simplifies the equilibrium analysis of some rigid
bodies since the directions of the resultant forces at A and B
are thus known (along the line joining points A and B).

42. Three-Force Members
• When subjected to three forces, the forces are concurrent
or parallel

43. Example: 1
The lever ABC is pin-supported at A and connected to a
short link BD. If the weight of the members are negligible,
determine the force of the pin on the lever at A.

44. Example: 1 (contd.)
Free Body Diagrams
• BD is a two-force member
• Lever ABC is a three-force member
Equations of Equilibrium
Solving,
kN
F
kN
FA
32
.
1
07
.
1


0
45
sin
3
.
60
sin
;
0
0
400
45
cos
3
.
60
cos
;
0
3
.
60
4
.
0
7
.
0
tan 1




















 





F
F
F
N
F
F
F
A
y
A
x


45. A man raises a 10 kg joist, of
length 4 m, by pulling on a
rope.
Find the tension in the rope
and the reaction at A.
SOLUTION:
• Create a free-body diagram of the joist.
Note that the joist is a 3 force body
acted upon by the rope, its weight, and
the reaction at A.
• The three forces must be concurrent
for static equilibrium. Therefore, the
reaction R must pass through the
intersection of the lines of action of the
weight and rope forces. Determine the
direction of the reaction force R.
• Utilize a force triangle to determine
the magnitude of the reaction force R.
Example: 2

46. • Create a free-body diagram of the joist.
• Determine the direction of the reaction
force R.
 
 
 
636
.
1
414
.
1
313
.
2
tan
m
2.313
m
515
.
0
828
.
2
m
515
.
0
20
tan
m
414
.
1
)
20
45
cot(
m
414
.
1
m
828
.
2
45
cos
m
4
45
cos
2
1


















AE
CE
BD
BF
CE
CD
BD
AF
AE
CD
AB
AF


6
.
58


Example: 2 (contd.)

47. • Determine the magnitude of the reaction
force R.



38.6
sin
N
1
.
98
110
sin
4
.
31
sin


R
T
N
8
.
147
N
9
.
81


R
T
Example: 2 (contd.)

48. Exercises
 Engineering Mechanics - Statics, R.C. Hibbeler, 12th
Edition
• Q5.11 – Q5.24
• Q5.32 – Q5.37
• Q5.41 – Q5.45

49. QUIZ
1. If a support prevents translation of a body, then the
support exerts a ___________ on the body.
A) Couple moment
B) Force
C) Both A and B.
D) None of the above
2. Internal forces are _________ shown on the free body
diagram of a whole body.
A) Always
B) Often
C) Rarely
D) Never

50. QUIZ (contd.)
3. The beam and the cable (with a frictionless pulley at D)
support an 80 kg load at C. In a FBD of only the
beam, there are how many unknowns?
A) 2 forces and 1 couple moment
B) 3 forces and 1 couple moment
C) 3 forces
D) 4 forces

51. QUIZ (contd.)
4. Internal forces are not shown on a free-body diagram
because the internal forces are_____.
A) Equal to zero
B) Equal and opposite and they do not affect the
calculations
C) Negligibly small
D) Not important

52. QUIZ (contd.)
5. The three scalar equations  FX =  FY =  MO = 0,
are ____ equations of equilibrium in two dimensions.
A) Incorrect B) The only correct
C) The most commonly used D) Not sufficient
6. A rigid body is subjected to forces.
This body can be considered
as a ______ member.
A) Single-force B) Two-force
C) Three-force D) Six-force