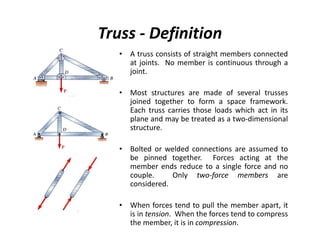
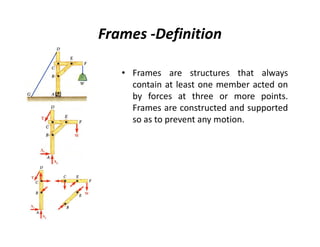
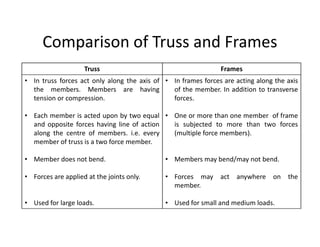
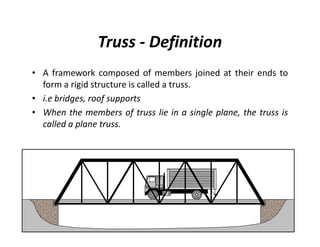
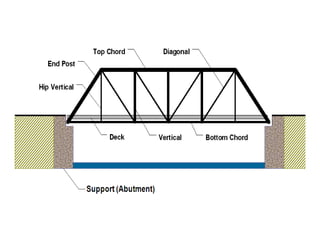
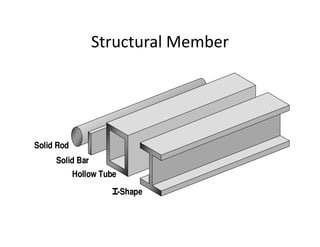
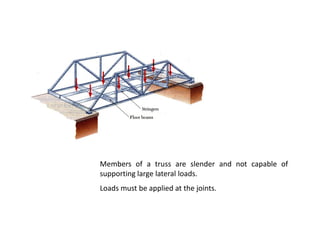
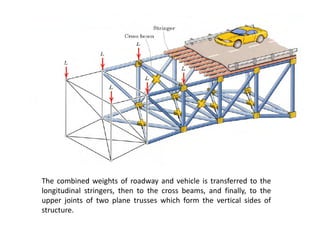
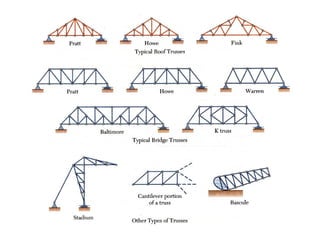
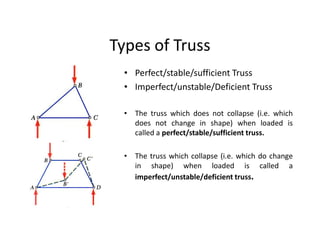
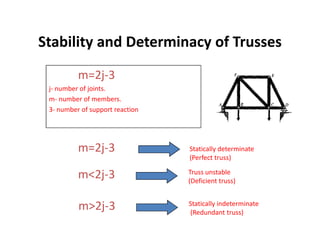
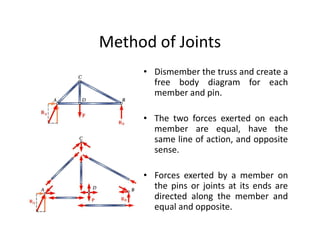
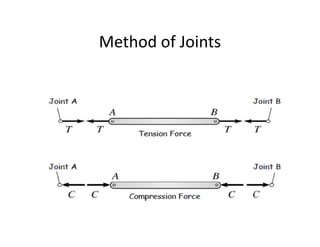
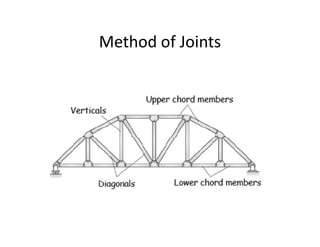
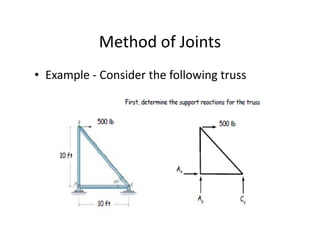
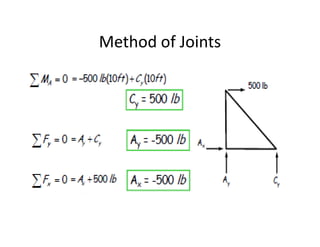
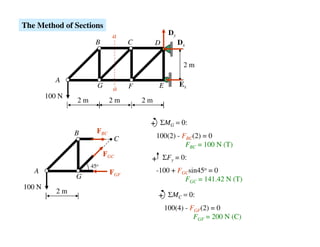
The document discusses frames and trusses, which are structures consisting of bars, rods, angles, and channels pinned or fastened together to support loads and transmit them to supports. Trusses contain only two-force members that experience either tension or compression, while frames can contain multi-force members and experience transverse forces as well. Common truss configurations include pinned, gusset plate, and bolted or welded joints. Trusses are analyzed using methods of joints or sections to determine member forces.

2. Trusses and Frames
• Frames and trusses are the structures consisting of bars, roads,
angle section, channel section etc. pinned/hinged/rivetted/welded
together to form a rigid structures.
• The function of the frame/truss is to support loads and transmit the
same to the support through the various members of the
frame/truss.
• Three categories of engineering structures are considered:
a) Frames: contain at least one multi-force member, i.e., member
acted upon by 3 or more forces.
b) Trusses: formed from two-force members, i.e., straight members
with end point connections
c) Machines: structures containing moving parts designed to
transmit and modify forces.

3. Truss - Definition
• A truss consists of straight members connected
at joints. No member is continuous through a
joint.
• Most structures are made of several trusses
joined together to form a space framework.
Each truss carries those loads which act in its
plane and may be treated as a two-dimensional
structure.
• Bolted or welded connections are assumed to
be pinned together. Forces acting at the
member ends reduce to a single force and no
couple. Only two-force members are
considered.
• When forces tend to pull the member apart, it
is in tension. When the forces tend to compress
the member, it is in compression.

4. Frames -Definition
• Frames are structures that always
contain at least one member acted on
by forces at three or more points.
Frames are constructed and supported
so as to prevent any motion.

5. Comparison of Truss and Frames
Truss Frames
• In truss forces act only along the axis of • In frames forces are acting along the axis
the members. Members are having of the member. In addition to transverse
tension or compression. forces.
• Each member is acted upon by two equal • One or more than one member of frame
and opposite forces having line of action is subjected to more than two forces
along the centre of members. i.e. every (multiple force members).
member of truss is a two force member.
• Member does not bend. • Members may bend/may not bend.
• Forces are applied at the joints only. • Forces may act anywhere on the
member.
• Used for large loads. • Used for small and medium loads.

6. Types of Truss Connections
Pinned Gusset Plate
Connection Connection

7. Truss - Definition
• A framework composed of members joined at their ends to
form a rigid structure is called a truss.
• i.e bridges, roof supports
• When the members of truss lie in a single plane, the truss is
called a plane truss.

9. Structural Member
Solid Rod
Solid Bar
Hollow Tube
-Shape

10. Members of a truss are slender and not capable of
supporting large lateral loads.
Loads must be applied at the joints.

11. The combined weights of roadway and vehicle is transferred to the
longitudinal stringers, then to the cross beams, and finally, to the
upper joints of two plane trusses which form the vertical sides of
structure.

13. Uses of truss
• Roof of factory shade.
• Ware house
• Railway platform
• Garage shed
• Transmission towers
• Crane truss
• Bridge Truss
• Sport Stadium Truss

20. Types of Truss
• Perfect/stable/sufficient Truss
• Imperfect/unstable/Deficient Truss
• The truss which does not collapse (i.e. which
does not change in shape) when loaded is
called a perfect/stable/sufficient truss.
• The truss which collapse (i.e. which do change
in shape) when loaded is called a
imperfect/unstable/deficient truss.

21. Stability and Determinacy of Trusses
m=2j-3
j- number of joints.
m- number of members.
3- number of support reaction
m=2j-3 Statically determinate
(Perfect truss)
m<2j-3 Truss unstable
(Deficient truss)
m>2j-3 Statically indeterminate
(Redundant truss)

22. Loads on Truss
• Weight of the roof
• Wind load acting on the roof
• Travelling loads of cars, trucks, trains etc. On the bridge
structure
• Weight of the structure it self. ( Generally Neglected)
• Reactions at the supports.

23. Internal Stresses in the Members
• Members of the truss transmit the load acting on it to the
support. In transmitting the loads, members are subjected to
either compressive stresses or tensile stresses.
• Member subjected to compression is called
a strut.
• Member subjected to tensile is called a Tie.

24. Assumptions for Analysis of Truss
• Truss joints are frictionless pin joints. They cannot resist
moments.
• Load are applied only at the joints.
• Truss members are straight and uniform in section.
• Each member of the truss is subjected to axial force only.
• The truss is assumed perfect.(i.e. m= 2j-3)
• Members of truss has negligible weight as compare to the
loads applied.
• Each member of the truss is two force member.
• The truss is rigid and does not change in shape.

25. Methods of analysis of Truss
1. Method of joints
2. Method of sections

26. Method of Joints
• If a truss is in equilibrium, then each of its joints must be in
equilibrium.
• The method of joints consists of satisfying the equilibrium
equations for forces acting on each joint.
Σ Fx = 0, Σ Fy = 0, Σ M = 0
• Methods of joint is most suited when forces in all the
members are required to be obtained.

27. Method of Joints
• Steps
• Decide whether a truss is perfect or not, using equation; m = 2j-3.
• Find support reactions for simply supported truss, using three conditions
of equilibrium.
– Considering entire truss as a single unit.
• Force acting at all the joints are coplanar concurrent and assumed to be in
static equilibrium and hence
– (i) apply (a) Σ H= 0 and (b) Σ V= 0 for the purpose of analysis.
– Or (ii) since the forces acting at the joints are in equilibrium, plot all
the forces in magnitude and direction to get either a closed force
triangle or closed force polygon .
• Each members of the truss is assumed to be in equilibrium hence apply
equal, opposite and collinear forces at the two ends along the centre line
of the member.
• Start the analysis only with a joint where there are only two unknowns.
Do not start the analysis with a joint where unknowns are more than two.
– Since, Σ H= 0 and (b) Σ V= 0 provide only two equations to solve the
unknowns.

28. Method of Joints
• Dismember the truss and create a
free body diagram for each
member and pin.
• The two forces exerted on each
member are equal, have the
same line of action, and opposite
sense.
• Forces exerted by a member on
the pins or joints at its ends are
directed along the member and
equal and opposite.

29. Method of Joints

30. Method of Joints

31. Method of Joints
• Example - Consider the following truss

32. Method of Joints

33. Method of Joints

35. Methods of Sections
• The method of joints is most effective when the forces in all
the members of a truss are to be determined.
• If however, the force is only one or a few members are
needed, then the method of sections is more efficient.

36. Methods of Sections
• In this method section is taken to
divide the truss into two parts,
cutting the truss along the members
in which the forces are required to
be found out.
• After cutting the truss into two parts
external forces are drawn on each
part of the truss and forces are also
drawn acting in the cut members.
• Apply the equilibrium condition:
• Fx = 0, Σ Fy = 0, Σ M = 0

37. Methods of Sections
• Cutting a truss care should be taken, not to cut more than
three members of the truss at one time in which the forces
are not known.

38. The Method of Sections
a Dy
B C D Dx
2m
A
G F E Ex
a
100 N
2m 2m 2m
+ ΣMG = 0:
B FBC
C 100(2) - FBC(2) = 0
FBC = 100 N (T)
FGC
+ ΣFy = 0:
45o
A FGF -100 + FGCsin45o = 0
G FGC = 141.42 N (T)
100 N
2m
+ ΣMC = 0:
100(4) - FGF(2) = 0
FGF = 200 N (C)

39. Any Question?

40. Thank you