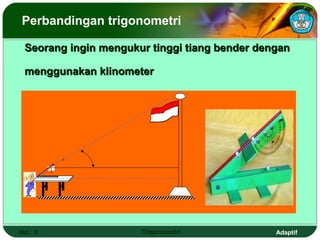
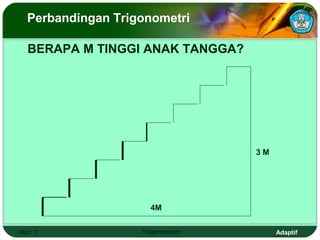
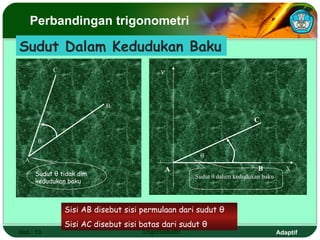
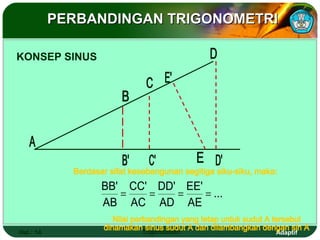
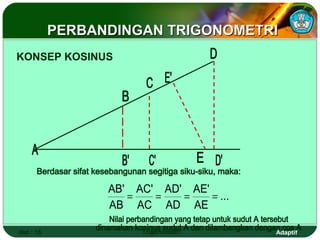
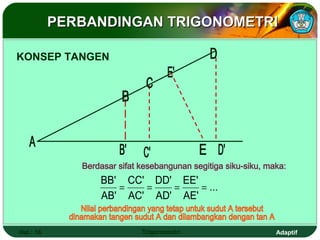
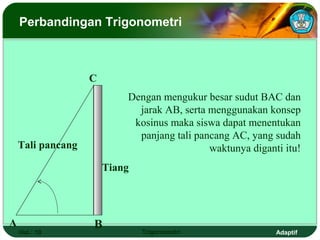
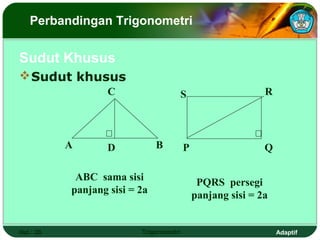
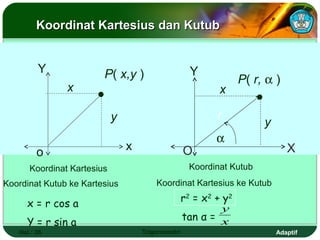
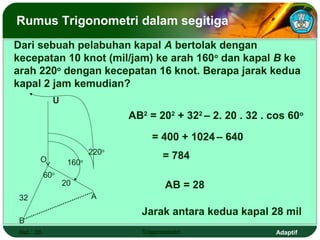
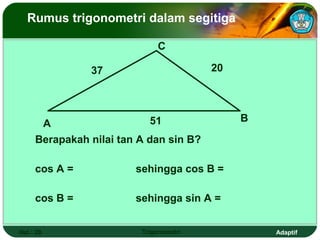
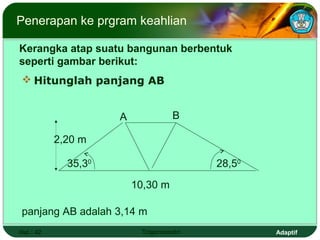
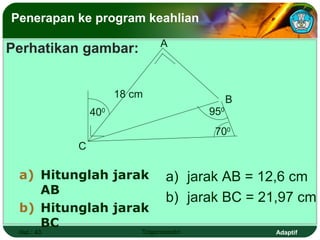
Dokumen ini adalah modul pembelajaran tentang perbandingan, fungsi, persamaan, dan identitas trigonometri yang terdiri dari beberapa bagian, termasuk penerapan trigonometri dalam masalah kejuruan, prasyarat pembelajaran, petunjuk penggunaan modul, dan peran guru. Modul ini bertujuan agar siswa dapat memahami konsep bilangan real dan menerapkan berbagai rumus trigonometri untuk menyelesaikan masalah. Selain penjelasan, modul ini dilengkapi dengan soal evaluasi untuk mengukur penguasaan kompetensi siswa.

1. Perbandingan ,fungsi, persamaan
dan
identitas trigonometri

2.  I. PENDAHULUAN
 I.I DESKRIPSI
 Modul siswa tentang bilangan real ini terdiri atas 4 baian prosesbpemelajaran yang meliputi :
 1. Menerapkan perbndingan trigonometri suatu sudut dalam menyelesaikan masalah kejuruan.
 2. Mengkonversi koordinat cartesius dan kutub, perbandingan penerapan dalam menyelesaikan
masalah kejuruan.
 3. Menerapkan aturan sinus dan cosinus dan menentukan luas segitiga dalam menyelesaikan
masalah kejuruan.
 4. Menerapkan rumus jumlah dan selisih dua sudut.
 5. Menyelesaikan persamaan trigonometri.
 Selain penjelasan materi, modul ini juga di lengkapi dengan soal evaluasi yng berbentuk “LKS”.
Soal evaluasi ini juga berguna sebagai tolak ukur, apakah seseorang siswa sudah menguasai
kompetensi ini atau belum. Jika siswa telah menguasai, maka siswa dapat melanjutkan ke
kompetensi berikutnya.
Hal.: 2 Isi dengan Judul Halaman Terkait Adaptif

3. I.2. PRASYARAT
 Kemampuan awal yang diperlukan untuk mempelajari modul
ini adalah peserta telah memahami operasi bilangan yang di
tunjukkan dengan garis bilangan atau operasi bilangan susun
ke bawah.
Hal.: 3 Isi dengan Judul Halaman Terkait Adaptif

4.  I.3. PETUNJUK PENGGUNAAN MODUL
 A. Penjelasan bagi siswa
 1. Pembelajaran yang dilaksanakan menggunakan sistem elf based learning
atau sistem pembelajaran mandiri. Diharapkan peserta didik dapat belajar
secara aktif dengan mengumpulkan berbagai sumber selain modul ini,
misalya melalui buku paket, LKS, majalah, media elektronik atau melalui
internet.
 2. Dalam modul ini dituntut tersedianya bahan ajar yang lengkap meliputi :
 - papan tulis
 - spidol dan penghapus papantulis
 - penggaris
 - alat tulis, yaitu: buku, pensil, karet penghapus, dan lain-lain.
 3. Setelah menyelesaikan modul ini, peserta didik dapat melanjutkan ke
modul selanjutnya yaitu modul ke-5
 4. Guru atau instruktur berperan sebagai fasilitator dan pengarah dalam
semua materi di modul ini, sehingga diharapkan dapat terjadi komunikasi
timbal balik yang efektif dalam mempercepat proses penguasaan
kompetensi peserta didik.
Hal.: 4 Isi dengan Judul Halaman Terkait Adaptif

5. B. PERAN GURU
 a. Membantu peserta didik dalam merencanakan proses belajar utamanya dalam materi-
materi yang relatif baru bagi peserta didik
 b. Membimbing peserta didik melalui tugas-tugas pelatihan yang dijelaskan dalam tahap
belajar
 c . Membantu peserta didik dalam memahami konsep yang terdapat pada modul ini dan
menjawab pertanyaan peserta didik dalam mengenal proses belajar dan pencapaian jenjang
pengetahuan peserta didik.
 d. Membantu peserta didik untuk menentukan dan mengakses sumber tambahan lain yang
diperlukan untuk belajar
 E .Mengorganisaikan kegiatan belajar kelompok yang diperlukan
 f. Melaksanakan penilaian
 g. Menjelaskan kepada peserta didik mengenai bagian yang perlu untuk dibenahi dan
merundingkan rencana pemelajaran selanjutnya
 h. Mencatat pencapaian kemajuan peserta didik
Hal.: 5 Isi dengan Judul Halaman Terkait Adaptif

6.  C. TUJUAN AKHIR
 Setelah mempelajari modul ini, peserta didik diharapkan
untuk dapat :
 1. Konsep bilangan real
 2. menghitung dan mengoperasikan bilangan real
 3. Menggunakan konsep perbandingan, skala, dan persen
untuk menyelesaikan msalah kejuruan
 4. menyederhanakan bilangan berpangkat dan bentuk
akar
 5. Menerapkan operasi pada bilangan berpangkat dan
bentuk akar
Hal.: 6 Isi dengan Judul Halaman Terkait Adaptif

7.  D.KOMPETENSI
 Kompetensi : Menerapkan konsep matriks
 Durasi Pembelajaran : 18 jam @ 45 menit
 Kondisi kerja
 Dalam melaksanakan kompetensi ini harus didukung
dengan tersedianya :
 Buku paket Matematika SMK bidang keahlian
teknologi dan industri
 Peralatan yang terkait dengan pelaksanaan
kompetensi ini
Hal.: 7 Isi dengan Judul Halaman Terkait Adaptif

8. Perbandingan trigonometri
Seorang ingin mengukur tinggi tiang bender dengan
menggunakan klinometer
α
Hal.: 2 Trigonometri Adaptif

9. Perbandingan Trigonometri
Pengalaman Belajar
 Seorang siswa program keahlian bangunan ingin
praktik membuat rangka atap rumah dengan
ketentuan ukuran seperti gambar berikut. Maka
panjang x adalah …
2m
xm
3
4 m
Hal.: 3 Trigonometri Adaptif

10. Perbandingan Trigonometrri
Pengalaman Belajar
 Puncak suatu menara dilihat dari tempat A dengan sudut
elevasi 300 dan dilihat dari B dengan sudut elevasi 45 0
seperti pada gambar. Apabila jarak A dan B adalah 20
meter, berapa tinggi menara tersebut?
300 450
B
A
20 m
Hal.: 4 Trigonometri Adaptif

11. APA yang terjadi ?
Perbandingan Trigonometri
Apabila ada beberapa guru memberi tugas pada
muridnya sbb:
“Segitiga siku-siku ABC mempunyai sisi-sisi
AC=4, BC=6 dan AB=8. Tentukan besar sudut
A.”
Hal.: 5 Trigonometri Adaptif

12. Sekilas ???
Perbandingan Trigonometri
 Tidak ada yang aneh dalam soal yang diberikan
oleh guru tersebut?
 Murid ya mencoba menghitung besar sudut A
dengan terlebih dahulu menghitung nilai Sinus A
 Guru merasa tak bersalah
Hal.: 6 Trigonometri Adaptif

13. Perbandingan Trigonometri
BERAPA M TINGGI ANAK TANGGA?
3M
4M
Hal.: 7 Trigonometri Adaptif

14. Perbandingan Trigonometri
Manakah bangun yang kelilingnya
terpanjang?
1) 2)
3) 4)
Hal.: 8 Trigonometri Adaptif

15. Perbandingan Trigonometri
Ruang Lingkup
1. Perbandingan Trigonometri suatu sudut
2. Sudut-sudut Istimewa ( Khusus )
3. Rumus-rumus Trigonometri
4. Koordinat Kartesius dan Kutub
5. Aturan Sinus, Kosinus dan Luas segitiga
6. Identitas Trigonometri
7. Persamaan Trigonometri
Hal.: 9 Trigonometri Adaptif

16. Perbandingan Trigonometri
SINUS
ADALAH PERBANDINGAN ANTARA
SISI DIDEPAN SUDUT DENGAN
HIPOTENUSA PADA SUATU
SEGITIGA SIKU-SIKU
C AC
Sin AOC =
OC
0 A
Hal.: 10 Trigonometri Adaptif

17. Perbandingan Trigonometri
 Cosinus adalah nilai perbandingan antara sisi disampaing
sudut dengan hipotenua suatu segitiga siku-siku
C
OA
Cos AOB =
OC
O A
Hal.: 11 Trigonometri Adaptif

18. Perbandingan Trigonometri
 Tangen adalah nilai perbandingan antara sisi
didepan sudut dengan sisi disamping sudut
C
AC
Tan AOC = OA
O A
Hal.: 12 Trigonometri Adaptif

19. Perbandingan trigonometri
Sudut Dalam Kedudukan Baku
C Y
B
C
θ
θ
A
A B X
Sudut θ tidak dlm Sudut θ dalam kedudukan baku
kedudukan baku
Sisi AB disebut sisi permulaan dari sudut θ
Sisi AC disebut sisi batas dari sudut θ
Hal.: 13 Trigonometri Adaptif

20. PERBANDINGAN TRIGONOMETRI
KONSEP SINUS
BB' CC' DD' EE'
= = = = ...
AB AC AD AE
Hal.: 14 Trigonometri Adaptif

21. PERBANDINGAN TRIGONOMETRI
KONSEP KOSINUS
AB' AC' AD' AE'
= = = = ...
AB AC AD AE
Hal.: 15 Trigonometri Adaptif

22. PERBANDINGAN TRIGONOMETRI
KONSEP TANGEN
BB' CC' DD' EE'
= = = = ...
AB' AC' AD' AE'
Hal.: 16 Trigonometri Adaptif

23. Perbandingan trigonometri
Diketahui segitiga ABC, siku-siku di C. Panjang sisi AB = 10
cm, sisi BC = 5 cm. B
Nilai cos A dan tan A berturut-turut adalah ....
10 5
A C
? didapat 5V3
Maka diperoleh : sin A = ½
Jadi : cos A = ½ V3
tan A = 1/3 V3
Hal.: 17 Trigonometri Adaptif

24. Perbandingan Trigonometri
Dikembangkan Soal
C Dengan mengukur panjang
tangga BC, dan mengukur besa
sudut ABC, dan menggunakan
Tangga konsep sinus, maka siswa
ditugasi untuk menentukan
ketinggian lantai II dari dasar
lantai.
A B
Hal.: 18 Trigonometri Adaptif

25. Perbandingan Trigonometri
C
Dengan mengukur besar sudut BAC dan
jarak AB, serta menggunakan konsep
kosinus maka siswa dapat menentukan
panjang tali pancang AC, yang sudah
Tali pancang waktunya diganti itu!
Tiang
A B
Hal.: 19 Trigonometri Adaptif

26. Perbandingan Trigonometri
Sudut Khusus
 Sudut khusus
C S R
A D B P Q
ABC sama sisi PQRS persegi
panjang sisi = 2a panjang sisi = 2a
Hal.: 20 Trigonometri Adaptif

27. Perbandingan Trigonometri
Dengan menggunakan gambar di atas,
tentukan nilai perbandingan :
α 0o 300 450 600 900
sin α …. …. …. …. ….
cosα …. …. …. …. ….
tgα …. …. …. …. ….
ctgα …. …. …. …. ….
sec α …. …. …. …. ….
cos ecα …. …. …. …. ….
Hal.: 21 Trigonometri Adaptif

28. Perbandibgan Trigonometri
Sudut Khusus
45o sin 45o = ½ V2
V2 1 cos 45o = ½ V2
tan 45o = 1
45 o
90o
1 sin 30o = ½
cos 30o = ½ V3
30o
tan 30o = 1/3 V3
2 V3
sin 60o = ½V3
90o cos 60o = ½
60
o
1 tan 60o = V3
Hal.: 22 Trigonometri Adaptif

29. Perbandingan Trigonometry
RUMUS-RUMUS TRIGONOMETRI
A. Relasi/Rumus Dasar Fungsi Trigonometri
1. a. Relasi Kebalikan:
1 1 1
csc α = sinα sec α = cos α cot α = tan α
sinα
b. Relasi Pembagian: tan α = cosα
cos α
cot α = sin α
c. Relasi “Pythagoras”:
sin2α + cos2α = 1 (dan variasinya)
tan2α + 1 = sec2α
1 + cot2α = csc2α
Hal.: 23 Trigonometri Adaptif

30. Perbandingan Trigonometri
Sudut Berelasi
2. Fungsi trigonometri sudut-sudut yang berelasi
a. sin(90 – α)o = cos αo cos(90 – α)o = sin αo
tan(90 – α)o = cot αo cot(90 – α)o = tan αo
sec(90 – α)o = csc αo csc(90 – α)o = sec αo
b. sin(180 – α)o = sin α0 sin(180 + α)o = –sin αo
cos(180 – α)o = –cos α0 cos(180 + α)o = –cos αo
tan(180 – α)o = –tan α0 tan(180 + α)o = tan αo
c. sin(360 – α)o = –sin α0 sin(–αo) = –sin αo
cos(360 – α)o = cos α0 cos(–αo) = cos αo
tan(360 – α)o = –tan α0 tan(–αo) = –tan αo
Bernilai
Sin All
”+”
Tan Cos
Hal.: 24 Trigonometri Adaptif

31. Perbandingan Trigonometri
Hal Khusus
1. Jika αo + βo + γo = 180o , maka:
sin(α + β)o = sin(180 – γ)o = sin γo
cos(α + β)o = cos(180 – γ)o = –cos γo
sin ½ (α + β)o = sin(90 – ½ γ)o = cos ½ γo
cos ½ (α + β)o = cos (90 – ½ γ)o = sin ½ γo
2. Jika αo + βo + γo = 270o, maka:
sin(α + β)o = sin(270 – γ)o = –cos γo
cos(α + β)o = cos(270 – γ)o = –sin γo
Hal.: 25 Trigonometri Adaptif

32. Koordinat Kartesius dan Kutub
Y P( x,y ) Y
P( r, α )
x x
• •
y r
y
α
o x O X
Koordinat Kartesius Koordinat Kutub
Koordinat Kutub ke Kartesius Koordinat Kartesius ke Kutub
r2 = x2 + y2
x = r cos a y
tan α = x
Y = r sin a
Hal.: 26 Trigonometri Adaptif

33. Rumus Trigonometri dalam Segitiga
1.Aturan (rumus) sinus dalam segitiga ABC:
a b c
= =
sin α sin β sin γ
2. Aturan (rumus) kosinus:
b2 + c 2 − a 2
a2 = b2 + c2 – 2bc cos α cos α =
2bc
b2 = a2 + c2 – 2ac cos β atau
c2 = a2 + b2 – 2ab cos γ c2 + a2 − b2
cos β =
2ca
cos γ = a2 + b2 − c2
2ab
Hal.: 27 Trigonometri Adaptif

34. Rumus Trigonometri dalam segitiga
Dari sebuah pelabuhan kapal A bertolak dengan
kecepatan 10 knot (mil/jam) ke arah 160o dan kapal B ke
arah 220o dengan kecepatan 16 knot. Berapa jarak kedua
kapal 2 jam kemudian?
U
AB2 = 202 + 322 – 2. 20 . 32 . cos 60o
= 400 + 1024 – 640
220o
O = 784
160o
60o
20 AB = 28
32 A
Jarak antara kedua kapal 28 mil
B
Hal.: 28 Trigonometri Adaptif

35. Rumus trigonometri dalam segitiga
C
37 20
51 B
A
Berapakah nilai tan A dan sin B?
cos A = sehingga cos B =
cos B = sehingga sin A =
Hal.: 29 Trigonometri Adaptif

36. RUMUS FUNGSI TRIGONOMETRI DUA SUDUT
1. Rumus jumlah Rumus selisih
 sin(α + β) = sin α cos β + cos α sin sin(α – β) = sin α cos β – cos α sin β

β  cos(α – β) = cos α cos β + sin α sin β
 cos(α + β) = cos α cos β – sin α sin
β
tan α + tan β tan α − tan β
tan(α + β ) = tan (α − β ) =
1 − tan α tan β 1 + tan α tan β
2. Rumus sudut rangkap Rumus setengah sudut
 Sin 2α = 2 sin α cos α  2 sin2 ½ α = 1 - cos α
 Cos 2α = cos2α – sin2α  2 cos2 ½ α = 1 + cos α
2 tan α 1 − cos α
tan 2α = tan 2 1 α =
1 − tan 2 α
2
1 + cos α
sin α
tan 1 α =
2
1 + cos α
Hal.: 30 Trigonometri Adaptif

37. RUMUS FUNGSI TRIGONOMETRI DUA SUDUT
3. Rumus sudut rangkap tiga
Sin 3α = 3 sin α – 4 sin3 α
Cos 3α = 4cos3α – 3 cos α
3 tan α − tan 3 α
tan 3α =
1 − 3 tan 2 α
Hal.: 31 Trigonometri Adaptif

38. Rumus Jumlah, Selisih, dan Hasil Kali
Fungsi Sinus/Kosinus
1. Hasil kali sinus dan kosinus
 2 sin α cos β = sin(α + β) + sin(α – β)
 2 cos α sin β = sin(α + β) – sin(α – β)
 2 cos α cos β = cos(α + β) – cos(α – β)
 –2 sin α sin β = cos(α + β) – cos(α – β)
atau 2 sin α sin β = cos(α – β) – cos(α + β)
2. Jumlah dan Selisih Fungsi Sinus/Kosinus
 sin A + sin B = 2 sin ½ (A + B) cos ½ (A – B)
 sin A – sin B = 2 cos ½ (A + B) sin ½ (A – B)
 cos A + cos B = 2 cos ½ (A + B) cos ½ (A – B)
 cos A – cos B = –2 sin ½ (A + B) sin ½ (A – B)
Hal.: 32 Trigonometri Adaptif

39. IDENTITAS TRIGONOMETRI
 Identitas adalah suatu kalimat terbuka yang
bernilai benar untuk setiap pengganti nilai
variabelnya, misal : sin2α + cos2α = 1
 Buktikan !
sin x 1 + cos x
2 csc x = +
1 + cos x sin x
sec4θ – sec2θ = tan4θ + tan2θ
Hal.: 33 Trigonometri Adaptif

40. IDENTITAS TRIGONOMETRI
sin x 1+ cos x
Bukti: 1+ cos x
+
sin x
sin 2 x +(1 +cos x ) 2
=
(1 +cos x ) sin x
sin 2 x +1 +2 cos x +cos 2 x
=
(1 +cos x ) sin x
2 + cos x
2
=
(1 + cos x ) sin x
2
=
sin x
= 2 csc x =ruas kanan (terbukti)
Hal.: 34 Trigonometri Adaptif

41. IDENTITAS TRIGONOMETRI
Bukti:
Alternatif I Dari ruas kiri lternatif II Dari ruas kanan
 Ruas kiri: Ruas kanan:
sec4θ – sec2θ tan 4θ + tan 2θ
= sec2θ(sec2θ – 1) = tan 2θ(tan 2θ + 1)
= sec 2θ x tan 2θ = (sec 2θ – 1) sec 2θ
= (1 + tan 2θ) x tan 2θ = sec 4θ – sec 2θ
= tan 2θ + tan 4θ = ruas kiri (terbukti)
= tan 4θ + tan 2θ
= ruas kanan (terbukti)
Hal.: 35 Trigonometri Adaptif

42. Persamaan Trigonometri Sederhana
Rumus I :
1). Jika sin x° = sin α°
maka: x = α + k. 360° atau
x = (180° − α) + k. 360° , k ∈ B
2). Jika cos x° = cos α°
maka : x = α + k. 360° atau
x = − α + k. 360°, k ∈ B
3). Jika tan x° = tan α°
maka : x = α + k. 180° k ∈ B
Hal.: 36 Trigonometri Adaptif

43. PERSAMAAN TRIGONOMETRI
Rumus II : Pada keadaan sama dengan nol
1). Jika sin x° = 0
maka: x = k.180° , k ∈ B
2). Jika cos x° = 0
maka: x = 90° + k.180° , k ∈ B
3). Jika tan x° = 0
maka: x = k.180° , k ∈ B
Hal.: 37 Trigonometri Adaptif

44. PERSAMAAN TRIGONOMETRI
Rumus III : Persamaan mengandung harga negatif
1). Jika sin x° = - sin α° = sin (-α)°
maka: x = - α + k. 360° atau
x = (180° + α) + k. 360° , k ∈ B
2). Jika cos x° = - cos α° = cos (180 + α )°
maka: x = 180 + α + k. 360° atau
x = - 180° - α + k. 360° , k ∈ B
3). Jika tan x° = - tan α° = tan (-α)°
maka: x = - α + k. 180° , k ∈ B
Hal.: 38 Trigonometri Adaptif

45. PERSAMAAN TRIGONOMETRI
Contoh Soal
 Tentukan himpunan penyelesaian persamaan trigonometri
berikut: Untuk 0 ≤ x < 360:
1
 a) sin x = sin 40
0 0
b) cos 2x = 0
2
Jawab:
 a) sin x0 = sin 400 ⇒ x = 40 + k.360 atau x = (180 – 40) + k.360
 untuk k = 0 → x = 40 k = 0 → k = 140
 Jadi himpunan penyelesaiannya adalah {40, 140}
 adalah {30, 150, 210, 330}
Hal.: 39 Trigonometri Adaptif

46. PERSAMAAN TRIGONOMETRI
1
 b) cos 2x = 0
2
cos 2x 0 = cos 60 0
maka 2x = 60 + k.360 atau 2x = -60 + k.360
x = 30 + k.1 80 x = -30 + k.180
 untuk k = 0 → x = 30 Untuk k = 1 → x = 2100
 k = 1 → x = 150 k = 2 → x = 330
 Jadi himpunan penyelesaiannya adalah
{30, 150, 210, 330}
Hal.: 40 Trigonometri Adaptif

47. PERSAMAAN TRIGONOMETRI
Soal :
1.Diketahui segitiga ABC, AC =25 cm, BC=40 cm,
dan panjang garis tinggi dari C,yaitu CD=24 cm.
Nilai cos A dan tan B berturut-turut adalah ....
2. Dua kapal meninggalkan suatu pelabuhan
secara bersamaan. Kapal pertama berlayar
dengan arah 030° dengan kecepatan 8
km/jam, sedangkan kapal kedua berlayar
dengan arah 090° dengan kecepatan 10
km/jam. Jarak kedua kapal itu setelah
berlayar 3 jam adalah ... km
Hal.: 41 Trigonometri Adaptif

48. Penerapan ke prgram keahlian
Kerangka atap suatu bangunan berbentuk
seperti gambar berikut:
 Hitunglah panjang AB
A B
2,20 m
35,30 28,50
10,30 m
panjang AB adalah 3,14 m
Hal.: 42 Trigonometri Adaptif

49. Penerapan ke program keahlian
A
Perhatikan gambar:
18 cm B
400 950
700
C
a) Hitunglah jarak a) jarak AB = 12,6 cm
AB
b) jarak BC = 21,97 cm
b) Hitunglah jarak
BC
Hal.: 43 Trigonometri Adaptif