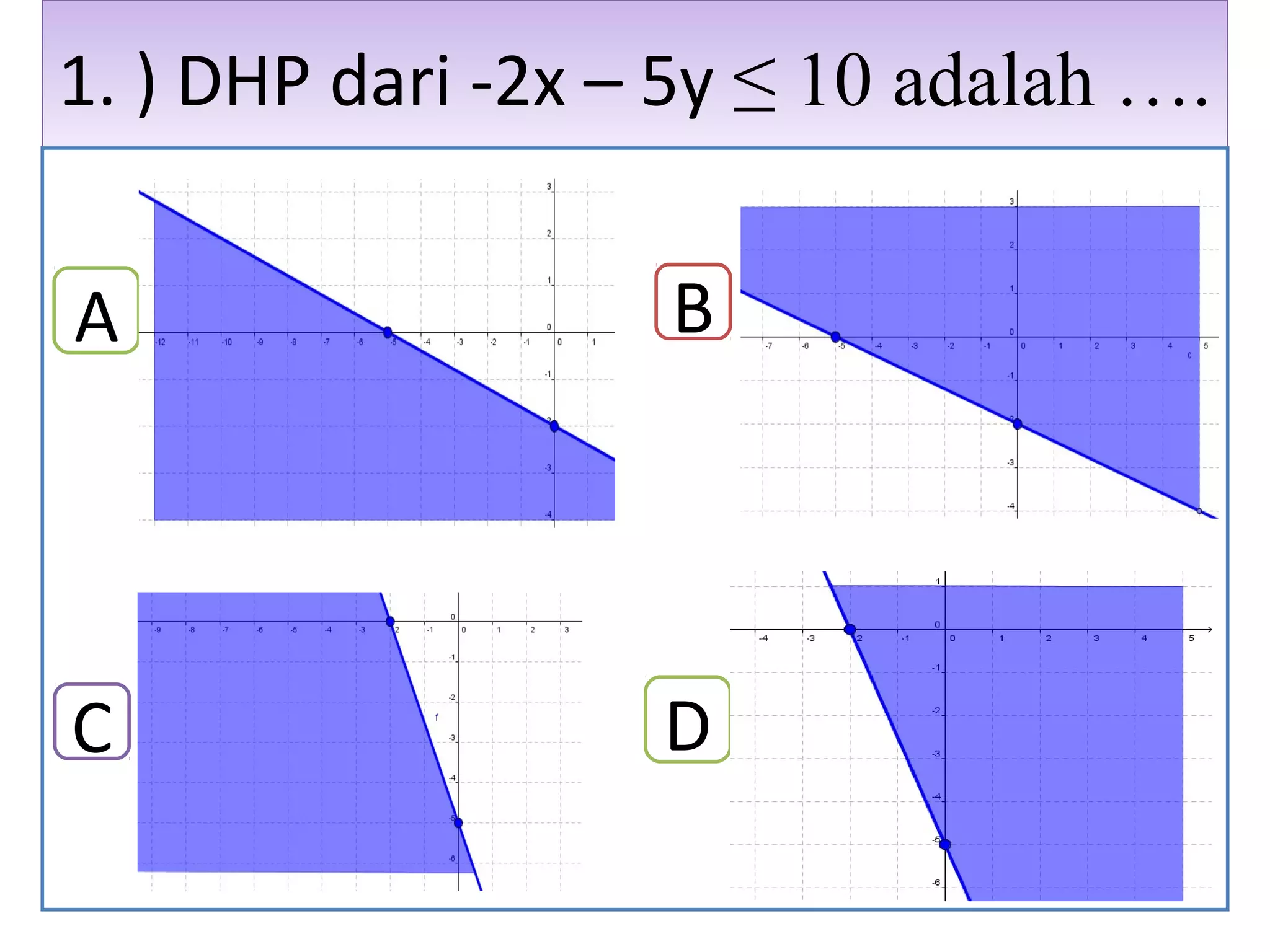
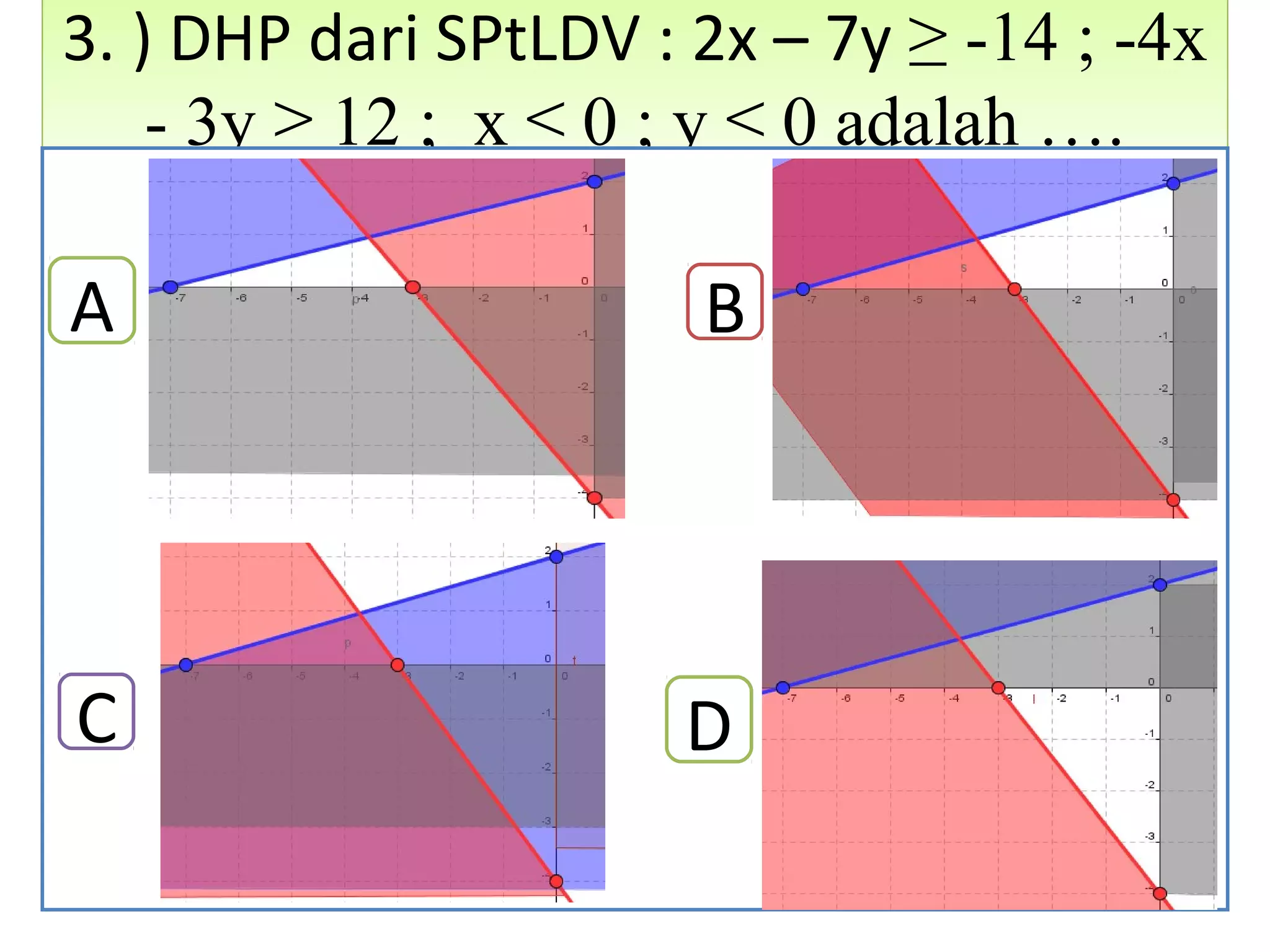
Dokumen ini membahas tentang sistem pertidaksamaan linear dua variabel (sptldv) dan langkah-langkah untuk melukis daerah himpunan penyelesaian (dhp). Terdapat penjelasan rinci mengenai cara menentukan titik potong dan melukis garis pembatas, serta memberikan contoh soal dan latihan. Selain itu, dokumentasi ini juga menyediakan kunci jawaban untuk latihan yang diberikan.

1. SISTEM PERTIDAKSAMAAN LINEAR
DUA VARIABEL (SPtLDV)
SISTEM PERTIDAKSAMAAN LINEAR
DUA VARIABEL (SPtLDV)
Oleh :
Santhi Rosalia Lestari
Magister Pendidikan Matematika
Universitas Sriwijaya
2016
Oleh :
Santhi Rosalia Lestari
Magister Pendidikan Matematika
Universitas Sriwijaya
2016
MATERIMATERI CONTOHCONTOH LATIHANLATIHAN

2. Melukis Daerah Himpunan
Penyelesaian (DHP)
Melukis Daerah Himpunan
Penyelesaian (DHP)
Kelas : X SMA
Kelompok : Matematika Peminatan
Ruang Lingkup : Aljabar
KI / KD : 3 / 3.2
Materi Pembelajaran : SPtLDV
Submateri : Melukis DHP dari
SPtLDV

3. Langkah-Langkah Melukis
Daerah Himpunan
Penyelesaian (DHP)
Langkah-Langkah Melukis
Daerah Himpunan
Penyelesaian (DHP)
1. Menentukan titik potong pada
tiap sumbu
2. Melukis garis pembatas
3. Menentukan DHP
Catatan :
Pada media pembelajaran ini, DHP
yang ditunjuk adalah daerah bersih.
1. Menentukan titik potong pada
tiap sumbu
2. Melukis garis pembatas
3. Menentukan DHP
Catatan :
Pada media pembelajaran ini, DHP
yang ditunjuk adalah daerah bersih.

4. 1. Menentukan titik potong
pada tiap sumbu
1. Menentukan titik potong
pada tiap sumbu
Untuk mendapatkan titik potong pada
sumbu x, substitusikan y = 0 ke persamaan
garis yang diketahui.
Dan untuk mendapatkan titik potong pada
sumbu y, substitusikan x = 0 ke persamaan
garis yang diketahui.
Untuk mendapatkan titik potong pada
sumbu x, substitusikan y = 0 ke persamaan
garis yang diketahui.
Dan untuk mendapatkan titik potong pada
sumbu y, substitusikan x = 0 ke persamaan
garis yang diketahui.

5. 2. Melukis garis pembatas2. Melukis garis pembatas
Hubungkan kedua titik potong pada
sumbu x dan sumbu y yang didapat (dari
langkah 1)
Hubungkan kedua titik potong pada
sumbu x dan sumbu y yang didapat (dari
langkah 1)

6. 3. Menentukan Daerah
Himpunan Penyelesaian (DHP)
3. Menentukan Daerah
Himpunan Penyelesaian (DHP)
Pada media ini, DHP adalah daerah bersih.
Maka, yang diarsir adalah yang BUKAN
daerah penyelesaian.
Jika pertidaksamaan mengandung ≥, maka
yang diarsir adalah daerah sebelah kiri
atau bawah. Dan jika pertidaksamaan
mengandung ≤, maka yang diarsir adalah
daerah sebelah kanan atau atas.
Pada media ini, DHP adalah daerah bersih.
Maka, yang diarsir adalah yang BUKAN
daerah penyelesaian.
Jika pertidaksamaan mengandung ≥, maka
yang diarsir adalah daerah sebelah kiri
atau bawah. Dan jika pertidaksamaan
mengandung ≤, maka yang diarsir adalah
daerah sebelah kanan atau atas.

7. ContohContoh
Lukislah DHP dari SPtLDV berikut :Lukislah DHP dari SPtLDV berikut :
0
0
1234
22
≥
≥
≤+
≤−
y
x
yx
xy

8. Melukis garis 2y – x = 2Melukis garis 2y – x = 2
Titik potong pada sumbu x, maka y = 0
2.0 – x = 2
- x = 2
x = -2 (-2,0)
Titik potong pada sumbu y, maka x = 0
2y – 0 = 2
2y = 2
y = 1 (0,1)

9. Melukis garis 2y – x = -2Melukis garis 2y – x = -2
22yy –– xx == --22

10. Melukis garis 4x + 3y = 12Melukis garis 4x + 3y = 12
Titik potong pada sumbu x, maka y = 0
4x + 3.0 = 12
4x = 12
x = 3 (3,0)
Titik potong pada sumbu y, maka x = 0
4.0 + 3y = 12
3y = 12
y = 4 (0,4)

11. Melukis garis 4x + 3y = 12Melukis garis 4x + 3y = 12
22yy –– xx == --22
4x+3y=12

12. Menentukan DHP dari :
2y – x ≥ -2 ; 4x + 3y ≤ 12 ; x ≥ 0 ; y ≥ 0
Menentukan DHP dari :
2y – x ≥ -2 ; 4x + 3y ≤ 12 ; x ≥ 0 ; y ≥ 0
2y – x = -2
4x+3y=12

13. Kita akan memulai untuk :Kita akan memulai untuk :
LATIHANLATIHAN

14. 1. ) DHP dari -2x – 5y ≤ 10 adalah ….1. ) DHP dari -2x – 5y ≤ 10 adalah ….
A B
C D

15. 2. ) DHP dari SPtLDV : x ≥ -3 ; y ≤ 1 adalah ….2. ) DHP dari SPtLDV : x ≥ -3 ; y ≤ 1 adalah ….
A B
C D

16. 3. ) DHP dari SPtLDV : 2x – 7y ≥ -14 ; -4x
- 3y ≥ 12 ; x ≤ 0 ; y ≤ 0 adalah ….
3. ) DHP dari SPtLDV : 2x – 7y ≥ -14 ; -4x
- 3y ≥ 12 ; x ≤ 0 ; y ≤ 0 adalah ….
A B
C D

17. 4. ) DHP dari SPtLDV : 3x + y ≥ 3; -3x +
5y ≤ -15 ; x ≤ 0 ; y ≥ 0 adalah ….
4. ) DHP dari SPtLDV : 3x + y ≥ 3; -3x +
5y ≤ -15 ; x ≤ 0 ; y ≥ 0 adalah ….
A B
C D

18. Klik untuk memeriksa hasil latihan
PERIKSAPERIKSA
Ulangi
Latihan
Ulangi
Latihan KUNCIKUNCI

19. Kunci jawaban latihan
1. B
2. A
3. D
4. C