GK
Uploaded byGur Kan
PPTX, PDF10,776 views

Switched capacitor

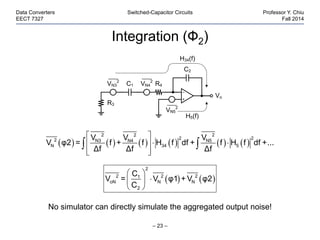
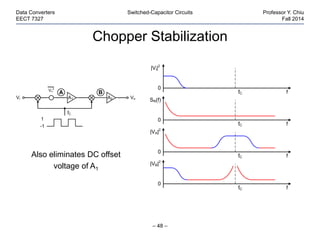
This document discusses switched-capacitor circuits. It begins by introducing the concept of using switched capacitors to emulate resistors and implement functions like integration. It then provides examples of basic switched-capacitor circuits like integrators. It discusses issues like noise and non-ideal effects in switched-capacitor circuits. It also provides examples of applications that use switched-capacitor circuits, such as filters, sigma-delta modulators, and pipelined ADCs.

Embed presentation

Downloaded 385 times
– 1 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Switched-Capacitor Circuits
Continuous-Time Integrator – 2 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Goal: C2 Vi Vo R1 C2 Vi Vo SC                t o in 1 2 -∞ o i 1 2 1 v t = - v ξ dξ R C V 1 1 H s = s = - V R C s Approach: emulating resistors with switched capacitors  1 2=R C
Concept of Switched Capacitor – 3 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014  A B q C i = = V - V T T   A B 1 i = V - V R Ф2 Ф1 eq T R = C • A switched capacitor is a discrete-time “resistor” • RC time constant set by capacitor ratio C2/C1 (match considerably better than R and C) and clock period T (flexibility) R VA VB i C Ф2Ф2 Ф1Ф1 VA VB <i> so,          2 eq,1 2 2 1 1 CT =R C = C = T C C Non-overlapping two-phase clock
Switched Capacitors – 4 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 • Shunt- and series-type SCs are simple and cheap to implement • Stray-insensitive SC requires 2 more switches, what’s the advantage besides being more flexible (i.e., w/ or w/o the T/2 delay)? 2-phase clock Ф2Ф1 VA VB CФ1 VA VB C Ф2 Series-typeShunt-type C Ф2Ф2(Ф1) Ф1Ф1(Ф2) VA VB Stray-insensitive
Discrete-Time Integrator (DTI) – 5 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 2-phase clock C2 Vi Vo Ф2Ф1 C1 Series-typeShunt-type Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 What are the VTFs (z-domain) of these DTIs, assuming no parasitic capacitance is present? C2 Vi Vo C1Ф1 Ф2
Shunt-Type DTI – 6 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф1 (sample) Charge conservation law (ideal): Total charge on C1 and C2 during Ф1→ Ф2 transition must remain unchanged! C2 Vi Vo C1 C2 Vo C1 Vi Ф2 (update)  Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 T vi(t) 0 t vo(t) 0 t (n-1) (n) (n+1) (n-1) (n) (n+1)
Shunt-Type DTI – 7 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф1 (sample) Ф2 (update) C2 Vi Vo C1 C2 Vo C1 Vi       1 i 1 o 2Q φ = V n C - V n C     2 1 o 2Q φ = 0 C - V n+1 C            1 2 i 1 o 2 1 o 2Q φ = Q φ ⇒ V n C - V n C = 0 C - V n+1 C      i 1 o 2 o 2V z C - V z C = -z V z C       -1 -1/2 o 1 1 -1 -1 i 2 2 V z C Cz z H z = = - or - V z C 1- z C 1- z
Series-Type DTI – 8 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф1 (sample/update) Ф2 (reset C1) C2 Vi Vo C1Ф1 Ф2       o 1 -1 i 2 V z C 1 H z = = - V z C 1- z VTF: Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 T vi(t) 0 t vo(t) 0 t (n-1) (n) (n+1) (n-1) (n) (n+1)
Stray Capacitance – 9 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Series-typeShunt-type Cu Cu Cu Cu Cu C1 C2 • Strays derive from D/S diodes and wiring capacitance • VTF is modified due to strays • Strays at the summing node is of no significance (virtual ground) 2 1 C = 4 C C2 Vi Vo C1 Ф1 Ф2 A C2 Vi Vo C1 Ф1 Ф2 A
Stray-Insensitive SC Integrator – 10 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014   1 -1 2 C 1 H z = - C 1- z VTF:   -1 1 -1 2 C z H z = + C 1- z • Capacitors can be significantly sized down to save power/area • Sizes are eventually limited by kT/C noise, mismatch, etc. C1 Ф2Ф2(Ф1) Ф1Ф1(Ф2) C2 Vi Vo A B “Inverting” “Non-inverting” VTF:
SC Amplifier – 11 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014    -11 2 C H z = + z C • Non-integrating, memoryless (less the delay) • Used in many applications of parametric amplification VTF: Vi C2 C1Ф1 Ф2 Ф1 Vo
– 12 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 SC Applications
CT Filter – 13 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 R CVi Vo L R1 CA R R R3 R4 CB R2 Vi Vo RLC prototype Active-RC Tow-Thomas CT biquad 
SC DT Filter – 14 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 SC DT biquad CA CB Vi Vo C1 Ф2Ф2 Ф1Ф1 C2 C4 Ф2 Ф1 C3 Ф2Ф1 Ф1Ф2 Ф2 R1 CA R R R3 R4 CB R2 Vi Vo Active-RC Tow-Thomas CT biquad 
Sigma-Delta (ΣΔ) Modulator – 15 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 CI Ф2Ф1 Ф1Ф2 Vi Do +VR 1-b DAC-VR CS DTI + 1-bit comparator + 1-bit DAC = first-order ΣΔ ADC
Pipelined ADC – 16 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 SC amplifier + 2 comparators + 3-level DAC = 1.5-bit pipelined ADC Vo Vi 0 -VR VR 1.5-b DAC Φ1 C1 Φ1 C2 Φ2 Φ1 Φ2 -VR/4 VR/4
SC Common-Mode Feedback – 17 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Vo + Vo - R A R VBias Vcm Vcmc Vo + Vo - R A R Vcmc Vcm-VBias  CM sense amp can be replaced by a floating voltage source since the gain through the main op-amp is high enough.
SC Common-Mode Feedback – 18 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014  Vo + Vo - A Vcmc C C 0.2C 0.2C Ф2 Ф2 Ф2 Ф1 Ф1 Ф1 Vcm Vcm VBias Vo + Vo - A Vcmc Vcm-VBias Vcm-VBias Ф2 Ф1
– 19 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Noise in SC Circuits
Noise of CT Integrator – 20 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Noise in CT circuits can be simulated with SPICE (.noise) R C Vi Vo R C Vo VN1 2 VN2 2 H1(f) H2(f)           2 2 2 22 N1 N2 oN 1 2 V V V = f H f df + f H f df +... Δf Δf
Noise of SC Integrator – 21 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 SC circuits are NOT noise-free! Switches and op-amps introduce noise. Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 C2 C1 Ф2Ф1 Ф1Ф2 Vi Vo
Sampling (Ф1) Ideal Voltage Source – 22 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Noise is indistinguishable from signal after sampling • The noise acquired by C1 will be amplified in Ф2 just like signal                       2 2 ∞ 22 N1 N2 N 10 2 ∞ 1 20 1 2 V V V φ1 = f + f H f df Δf Δf 1 = 4kTR +4kTR df 1+ j2πf R +R C kT = C C1 Vi R1 R2 VN1 2 VN2 2
Integration (Ф2) – 23 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 No simulator can directly simulate the aggregated output noise!                       2 22 2 22 N3 N5N4 N 34 5 V VV V φ2 = f + f H f df + f H f df +... Δf Δf Δf           2 2 2 21 oN N N 2 C V = V φ1 + V φ2 C Vo VN3 2 VN5 2 H34(f) H5(f) C1 C2 R4VN4 2 R3
Sampling (Ф1) Noise – Cascaded Stages – 24 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 C1'R1 R2 VN3 2 VN5 2 VN1 2 VN2 2 C1 C2 R4VN4 2 R3 • Finite op-amp BW limits the noise bandwidth, resulting in less overall kT/C noise (noise filtering). • But parasitic loop delay may introduce peaking in freq. response, resulting in more integrated noise (noise peaking). C2 C2' Vi Vo C1 Ф1Ф2 Ф2Ф1 C1' Ф2Ф1 Ф1Ф2 Ф2 
Sampled Noise Spectrum – 25 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Total integrated noise power remains constant • SNR remains constant CT DT PSD fs/2 fs 3/2fs 0 PSD fs 2fs 0 Alias
– 26 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Non-ideal Effects in SC Circuits
Non-ideal Effects in SC Circuits – 27 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Capacitors (poly-poly, metal-metal, MIM, MOM, sandwich, gate cap, accumulation-mode gate cap, etc.) – PP, MIM, and MOM are linear up to 14-16 bits (nonlinear voltage coefficients negligible for most applications) – Gate caps are typically good for up to 8-10 bits • Switches (MOS transistors) – Nonzero on-resistance (voltage dependent) – (Nonlinear) stray capacitance added (Cgs, Cgd, Cgb, Cdb, Csb) – Switch-induced sampling errors (charge injection, clock feedthrough, junction leakage, drain-source leakage, and gate leakage) • Operational amplifiers – Offset – Finite-gain effects (voltage dependent) – Finite bandwidth and slew rate (measured by settling speed)
– 28 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Non-ideal Effects of Switches
Nonzero On-Resistance – 29 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • FET channel resistance (thus tracking bandwidth) depends on signal level • Usually (RonCS)-1 ≥ (3-5)·ω-3dB of closed-loop op-amp for settling purpose VGS Vout C … Ф CS Ф Ф CS … Ron 0 VDDVout VTnVTp PMOS NMOS CMOS  -1 on ox DD th out W R = μC V - V - V L
Clock Bootstrapping – 30 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Small on-resistance leads to large switches → large parasitic caps and large clock buffers • Clock bootstrapping keeps VGS of the switch constant → constant on- resistance (body effect?) and less parasitics w/o the PMOS Ф Ф CS … OutIn M1 VDD Ф1 Ф2 CMOS Bootstrapped NMOS
Simplified Clock Bootstrapper – 31 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Pros • Linearity • Bandwidth Cons • Device reliability • Complexity Out C In M2 M1 VDD VSS OutIn M1 VDD Ф1 Ф2 Ф1 Ф1 Ф2 Ф2 Ф2 Ф2
Switch-Induced Errors – 32 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Channel charge injection and clock feedthrough (on drain side) result in charge trapped on CS after switch is turned off. Vout Ф CS Zi Vin CgdCgs Qch • Clock feedthrough • Charge injection
Clock Feedthrough and Charge Injection – 33 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Both phenomena sensitive to Zi, CS, and clock rise/fall time • Offset, gain error, and nonlinearity introduced to the sampling • Clock feedthrough can be simulated by SPICE, but charge injection cannot be simulated with lumped transistor models Ф VDD 0 Vin+Vth Switch on Switch off Vout Ф CS Zi Vin CgdCgs Qch
Clock Rise/Fall-Time Dependence – 34 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф VDD 0 Vin+Vth Switch on Switch off Vout Ф CS Zi Vin CgdCgs Qch Clock feedthrough Charge injection Fast turn-off Slow turn-off gs DD gs S C ΔV = - V C +C     ox DD th in gs S C WL V - V - V ΔV = - 2 C +C  gs in th gs S C ΔV = - V + V C +C ΔV = 0
Dummy Switch – 35 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Difficult to achieve precise cancellation due to the nonlinear dependence of ΔV on Zi, CS, and clock rise/fall time • Sensitive to the phase alignment between Ф and Ф_ Vout Ф W L CS W 2L Ф Vin
CMOS Switch – 36 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Very sensitive to phase alignment between Ф and Ф_ • Subject to threshold mismatch between PMOS and NMOS • Exact cancellation occurs only for one specific Vin (which one?) Vout CS Vin Ф Ф Same size for P and N FETs
Differential Signaling – 37 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Signal-independent errors (offset) and even-order distortions cancelled • Gain error and odd-order nonlinearities remain Balanced diff. input Vop CSp Vip M1 Von CSn Vin M2 Ф Ф
Switch Performance – 38 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014     ch 2 ithDDox 2 ithDDox on μQ L VVVWLμC L VVV L W μC 1 R      S ch C Q 2 1 ΔV Charge injection: Bandwidth: S 2 ch Son CL μQ CR 1 BW   2 2 ch S S ch Q L CΔV 1 L ≈ = BW 2 C μQ 2μ Performance FoM: Technology scaling improves switch performance! On-resistance:
Leakage in SC Circuits – 39 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • I1 – diode leakage (existing in the old days too) • I2 – sub-threshold drain-source leakage of summing-node switch • I3 – gate leakage (FN tunneling) of amplifier input transistors • Leakage currents are highly temperature- and process-dependent; the lower limit of clock frequency is often determined by leakage Vo(t) 0 t Ф1 Ф1Ф2 Ф2 Φ1 = “high”, Φ2 = “low” Vi Vo C2 C1 A0 Vx Ф2 Ф2 Ф1 Ф1 VB I2 I1 I3
DS Leakage – 40 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 M1 + Vi + Vo + Vo - Vi - CS + CS - VDD M1 - VDD Ф1 Ф1e Ф1 Ф1e Ф2 Ф2 CS + CS - Ф2e Ф2e • 0.13-μm CMOS • A0 = Gm·Ro = 90dB • Ro ≈ 2MΩ • Rleak ≈ 0.6V/3μA ≈ 0.2MΩ • A0 = Gm·(Rleak//Ro) ≈ 70dB OutIn M1 VDD Φ Φ Φ Out Φ Φ Φ Φ Φ Φ Φ In M3 M4 M2 M1 Ileak VDD = 1.2V VSS = 0V
Gate Leakage – 41 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Direct tunneling through the thin gate oxide • Short-channel MOSFET behaves increasingly like BJT’s • Violates the high-impedance assumption of the summing node     GS ox GSI ∝ WL exp -t exp V
Switch Size Optimization – 42 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • To minimize switch-induced error voltages, small transistor size, slow turn-off, low source impedance should be used. • For fast settling (high-speed design), large W/L should be used, and errors will be inevitably large as well. Guidelines • Always use minimum channel length for switches as long as leakage allows. • For a given speed, switch sizes can be optimized w/ simulation. • Be aware of the limitations of simulators (SPICE etc.) using lumped device models.
– 43 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Non-ideal Effects of Op-Amps
Non-ideal Effects of Op-Amps – 44 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Offset • Finite-gain effects (voltage dependent) • Finite bandwidth and slew rate (measured by settling speed)
Offset Voltage – 45 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014         1 i 1 o os 2Q φ = V n C + V n - V C       2 os 1 o os 2Q φ = -V C + V n+1 - V C     -1 1 o i-1 2 C z V z = V z C 1- z Vi Vo C2 C1Ф1 Ф2 Ф2 Ф1 Vos Vo(t) 0 t Ф1 Ф1Ф2 Ф2 Vi = 0           1 i o o os 2 C V = 0 ⇒ V n+1 - V n = V C
Autozeroing – 46 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014       1 i os 1 os 2Q φ = V n - V C - V C       2 os 1 o os 2Q φ = -V C + V n - V C       o 1 i 2 V z C H z = = V z C Vi Vo C2 C1Ф1 Ф2 Ф2 Ф1 Vos Ф1 • Also eliminates low-frequency noise, e.g., 1/f noise • A.k.a. correlated double sampling (CDS)
Chopper Stabilization – 47 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ref: K. C. Hsieh, P. R. Gray, D. Senderowicz, and D. G. Messerschmitt, “A low-noise chopper-stabilized differential switched-capacitor filtering technique,” IEEE Journal of Solid-State Circuits, vol. 16, issue 6, pp. 708-715, 1981. Vi VoA1 Vn 2 A2 fC 1 -1 A B
Chopper Stabilization – 48 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Also eliminates DC offset voltage of A1 Vi VoA1 Vn 2 A2 fC 1 -1 A B |Vi|2 f 0 SN(f) f 0 f 0 |VA|2 |VB|2 f 0 fC fC fC fC
Chopper-Stabilized Differential Op-Amp – 49 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Vi+ Vi- Vo- Vo+ Ф Ф Ф Ф Ф Ф Ф Ф • Integrators/amplifiers can be built using these op-amps • Some oversampling is useful to facilitate the implementation
Ideal SC Amplifier – 50 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 1 CL 2 C A = C • Closed-loop gain is determined by the capacitor ratio by design • But this is assuming X is an ideal summing node (the op-amp is ideal) Vi ∞ C2 C1Ф1 Ф2 Ф1 VoX
Finite-Gain Effect in SC Amplifier – 51 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014        o 1 1 1 2 CL 1 2i 2 2 2 2 V C C C +C1 A = = ≈ 1- C +CV C C C A1+ C A Vi A C2 C1Ф1 Ф2 Ф1 VoX                   1 i 1 x 1 1 2 x 1 o 1 x 1 Q φ = V φ - V φ C +0 C V φ = V φ = -V φ A         1 2 i 1 x 1 o x 2Q φ = Q φ ⇒ V C = -V C + V - V C                   2 x 2 1 o 2 x 2 2 o 2 x 2 Q φ = -V φ C + V φ - V φ C V φ = -V φ A o xV = -V A
– 52 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Practical Issues
Analog vs. Digital Supply Lines – 53 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Sharing sensitive analog supplies with digital ones is a very bad idea. Analog circuits Digital circuits Pad Pad VDD CBP id= d L di ΔV =L dt R dΔV =i R A DD L RV = V - ΔV - ΔV
Analog vs. Digital Supply Lines – 54 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Dedicated pads for analog and digital supplies • On-chip bypass capacitors help (watch ringing) • Off-chip chokes (large inductors) can stop noise propagation at board level Analog circuits Digital circuits Pad Pad VDD CBP Pad Pad id=
“Supply” Capacitance – 55 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Any summing-node stray capacitance can be a potential coupling path. • VDD, VSS, substrate, clock line, and digital noises, body effect, etc. • Fully differential circuits help to reject common-mode noise and coupling. Cp … VDD VSS M2 M5 M3 M4 M7 M6 Vo CC Vi C2 C1Ф1 Ф2 Ф2 Ф1 M1 S Y X Cgs Cgd  stray o 2 C ΔV = ΔV C
“Supply” Capacitance – 56 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Avoid connecting bottom-plate parasitics to the summing node • Avoid crossing other signal lines with the summing node • Shielding can mitigate substrate noise coupling n substrate p+ p well Cbot C2
Clock Generation – 57 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Clock-gated ring structure • Non-overlapping time determined by inverter delays, sensitive to process, voltage, and temperature (PVT) variations • DLL is an alternative, often used in high-speed designs CLK Ф2 Ф1 Ф2 Ф1

More Related Content

PPTX
Active filters
byNEW HORIZON COLLEGE OF ENGINEERING
 
PPTX
LIC UNIT III.pptx
byArunS118525
 
PDF
Pll and vco
byNEW HORIZON COLLEGE OF ENGINEERING
 
PPT
cmos Unit passive and active current mirrors 3 2023-24.ppt
byDimple Relekar
 
PPTX
Switched capacitor circuits_shish
byShishira S Venkatesha
 
PDF
EC3451 LINEAR INTEGRATED CIRCUITS UNIT 1 .pdf
byVanithaR25
 
PDF
Comparator
byRamen Dutta
 
PPTX
Neutralization Technique in EDC
byvimaladevi s
 
Active filters
byNEW HORIZON COLLEGE OF ENGINEERING
 
LIC UNIT III.pptx
byArunS118525
 
Pll and vco
byNEW HORIZON COLLEGE OF ENGINEERING
 
cmos Unit passive and active current mirrors 3 2023-24.ppt
byDimple Relekar
 
Switched capacitor circuits_shish
byShishira S Venkatesha
 
EC3451 LINEAR INTEGRATED CIRCUITS UNIT 1 .pdf
byVanithaR25
 
Comparator
byRamen Dutta
 
Neutralization Technique in EDC
byvimaladevi s
 

What's hot

PPT
Charged pump plls
byRabindranath Tagore University, Bhopal
 
PPTX
Pass Transistor Logic
bySudhanshu Janwadkar
 
PPTX
Cmos fabrication
byjigyashamaru
 
PPTX
Stick Diagram
byKalyan Acharjya
 
PDF
Phase-locked Loops - Theory and Design
bySimen Li
 
PDF
Ee6378 bandgap reference
byssuser2038c9
 
PPTX
Second order effects
byPRAVEEN KUMAR CHITLURI
 
PDF
io and pad ring.pdf
byquandao25
 
PPT
Latch up
byishan111
 
DOC
WPE
byAdrianOShaughnessy
 
PPSX
MOSFETs
byDr. A. B. Shinde
 
PPTX
Fm generation
bympsrekha83
 
PPT
Mosfet
byThen Murugeshwari
 
PPT
Mosfet unit 2
byMadhuriMulik1
 
PPTX
Power dissipation cmos
byRajesh Tiwary
 
PDF
Mos transistor
byMurali Rai
 
PPT
Analog Layout and Process Concern
byasinghsaroj
 
PPT
Pass Transistor Logic
byDiwaker Pant
 
PPTX
Short Channel Effect In MOSFET
bySudhanshu Srivastava
 
PPTX
MOS Capacitor
byA. S. M. Jannatul Islam
 
Charged pump plls
byRabindranath Tagore University, Bhopal
 
Pass Transistor Logic
bySudhanshu Janwadkar
 
Cmos fabrication
byjigyashamaru
 
Stick Diagram
byKalyan Acharjya
 
Phase-locked Loops - Theory and Design
bySimen Li
 
Ee6378 bandgap reference
byssuser2038c9
 
Second order effects
byPRAVEEN KUMAR CHITLURI
 
io and pad ring.pdf
byquandao25
 
Latch up
byishan111
 
WPE
byAdrianOShaughnessy
 
MOSFETs
byDr. A. B. Shinde
 
Fm generation
bympsrekha83
 
Mosfet
byThen Murugeshwari
 
Mosfet unit 2
byMadhuriMulik1
 
Power dissipation cmos
byRajesh Tiwary
 
Mos transistor
byMurali Rai
 
Analog Layout and Process Concern
byasinghsaroj
 
Pass Transistor Logic
byDiwaker Pant
 
Short Channel Effect In MOSFET
bySudhanshu Srivastava
 
MOS Capacitor
byA. S. M. Jannatul Islam
 

Viewers also liked

PPTX
Switched capacitor filter
byMinh Anh Nguyen
 
PPS
Switched capacitor filter
byMinh Anh Nguyen
 
PPT
Biquad Filter
byimran khan
 
PDF
ECE 626 project report Switched Capacitor
byKarthik Rathinavel
 
PDF
Design of a 45nm TIQ Comparator for High Speed and Low Power 4-Bit Flash ADC
byIDES Editor
 
PDF
Design & characterization of high speed power efficient cmos comparator
byIAEME Publication
 
PPTX
Converter Simulation - Beyond the Evaluation Board
byAnalog Devices, Inc.
 
PDF
A 10-BIT 25 MS/S PIPELINED ADC USING 1.5-BIT SWITCHED CAPACITANCE BASED MDAC ...
byIAEME Publication
 
PPT
Fft
byZulfiqar Khan
 
PPT
Lecture9
bybabak danyal
 
PDF
Cultura del agua en Frailes I: conoce tus fuentes y Acuíferos
byTúRInnova @tecnico_turismo
 
PDF
путешествие к настоящему (4)
byЯковлев Алексей
 
PPTX
hubungan tingkat pendidikan orangtua dengan prestasi hasil belajar anak
bySiti Nurjanah
 
PDF
Рекламные услуги Business Family
byBusiness Family
 
PDF
Рекламные услуги Business Family
byBusiness Family
 
PPTX
Thinks - Monday
byjwickberg
 
PDF
Интернет маркетинг по новым технологиям
byBusiness Family
 
PPTX
Ev90
by98031958726
 
PPTX
Enterprise Node - Code Discoverability
byKurtis Kemple
 
PPTX
Peta
bySiti Nurjanah
 
Switched capacitor filter
byMinh Anh Nguyen
 
Switched capacitor filter
byMinh Anh Nguyen
 
Biquad Filter
byimran khan
 
ECE 626 project report Switched Capacitor
byKarthik Rathinavel
 
Design of a 45nm TIQ Comparator for High Speed and Low Power 4-Bit Flash ADC
byIDES Editor
 
Design & characterization of high speed power efficient cmos comparator
byIAEME Publication
 
Converter Simulation - Beyond the Evaluation Board
byAnalog Devices, Inc.
 
A 10-BIT 25 MS/S PIPELINED ADC USING 1.5-BIT SWITCHED CAPACITANCE BASED MDAC ...
byIAEME Publication
 
Fft
byZulfiqar Khan
 
Lecture9
bybabak danyal
 
Cultura del agua en Frailes I: conoce tus fuentes y Acuíferos
byTúRInnova @tecnico_turismo
 
путешествие к настоящему (4)
byЯковлев Алексей
 
hubungan tingkat pendidikan orangtua dengan prestasi hasil belajar anak
bySiti Nurjanah
 
Рекламные услуги Business Family
byBusiness Family
 
Рекламные услуги Business Family
byBusiness Family
 
Thinks - Monday
byjwickberg
 
Интернет маркетинг по новым технологиям
byBusiness Family
 
Ev90
by98031958726
 
Enterprise Node - Code Discoverability
byKurtis Kemple
 
Peta
bySiti Nurjanah
 

Similar to Switched capacitor

PPTX
comparator.pptx
byPrasunSinghal2
 
PDF
Switched_Capacitors_Mixed_Signal_Design_Engineers_1678884175.pdf
bySouryaDewan1
 
PDF
STATE-SPACE AVERAGING METHOD
bySlobodan Cuk
 
PDF
Data Converters 2007th Edition Franco Maloberti
bylenyyyerai
 
PPT
modulation fm dengan menggunakan cd4046 secara penjelasan dengan frekwensi me...
byBariShobari
 
PDF
L 23(dp)(pe) ((ee)nptel)
byNikolaTesla18
 
PDF
Frequency dependency analysis for differential capacitive sensor
byjournalBEEI
 
PPT
PPT FINAL (1)-1 (1).ppt
bytariqqureshi33
 
PDF
Analysis
byChủ tịch Toàn
 
PDF
Parasitic consideration for differential capacitive sensor
byjournalBEEI
 
PDF
CAPACITIVE SENSORS ELECTRICAL WAFER SORT
byMassimo Garavaglia
 
PDF
Ppt iitr
byNIT MEGHALAYA
 
PDF
2001_Book_FundamentalsOfPowerElectronics.pdf
byLucianoCastelli4
 
PPTX
Nyquist-Rate D/A Converters presented by Oveis Dehghantanha
byoveis dehghantanha
 
PDF
book_cmos_Data_Converters-Franco-Maloberti
byVictorMatheusLima3
 
PDF
Progress 1st sem
byNIT MEGHALAYA
 
PDF
A Three Level Single Stage PFC Converter for Variable Power Applications
bypaperpublications3
 
PDF
IC Design of Power Management Circuits (III)
byClaudia Sin
 
PPT
Schuler Electronics Instructor CH07 amplifiers part 2.ppt
bySreejaSujith2
 
PPT
power conversion converters for energy conversion
byAliALKHAYYAT8
 
comparator.pptx
byPrasunSinghal2
 
Switched_Capacitors_Mixed_Signal_Design_Engineers_1678884175.pdf
bySouryaDewan1
 
STATE-SPACE AVERAGING METHOD
bySlobodan Cuk
 
Data Converters 2007th Edition Franco Maloberti
bylenyyyerai
 
modulation fm dengan menggunakan cd4046 secara penjelasan dengan frekwensi me...
byBariShobari
 
L 23(dp)(pe) ((ee)nptel)
byNikolaTesla18
 
Frequency dependency analysis for differential capacitive sensor
byjournalBEEI
 
PPT FINAL (1)-1 (1).ppt
bytariqqureshi33
 
Analysis
byChủ tịch Toàn
 
Parasitic consideration for differential capacitive sensor
byjournalBEEI
 
CAPACITIVE SENSORS ELECTRICAL WAFER SORT
byMassimo Garavaglia
 
Ppt iitr
byNIT MEGHALAYA
 
2001_Book_FundamentalsOfPowerElectronics.pdf
byLucianoCastelli4
 
Nyquist-Rate D/A Converters presented by Oveis Dehghantanha
byoveis dehghantanha
 
book_cmos_Data_Converters-Franco-Maloberti
byVictorMatheusLima3
 
Progress 1st sem
byNIT MEGHALAYA
 
A Three Level Single Stage PFC Converter for Variable Power Applications
bypaperpublications3
 
IC Design of Power Management Circuits (III)
byClaudia Sin
 
Schuler Electronics Instructor CH07 amplifiers part 2.ppt
bySreejaSujith2
 
power conversion converters for energy conversion
byAliALKHAYYAT8
 

Recently uploaded

PPTX
Environmental-Impact-of-Sustainable-Development.pptx
byyecamoy754
 
PPTX
GDG I²IT Freshers' Tech Kickoff Event, Pune
byshahvaibhavi221
 
PPTX
presentation-tenable-corporate-deck-ppt-version-english (1).pptx
bykrodriguez55
 
PPTX
Two Unethical Issue Engineers Practice.pptx
byhehbe481
 
PPTX
CFP_Unit 5. Structure and Functions pptx
bypawarbhaktiit
 
PDF
How to Write Research Papers NCBP D3.pdf
byDr. Rahul Pandya
 
PPTX
Ortho Graphic Projections for civil engineering.pptx
byUmairAli575718
 
PPT
Smart waste management using internet of things 2025.ppt
byJeganKalaimani
 
PPTX
Why Hydraulic Flushing Should Never Be Skipped Before Commissioning
byNeometrix_Engineering_Pvt_Ltd
 
PDF
TrakSYS Certified Engineer Certificate.pdf
byDjordje Zivanovic
 
PPTX
Training Notes_ SBPDCL Apprenticeship Program.pptx
bypevepe9073
 
PPTX
brpc_internal_share_jiangrujie_baidu_com.pptx
bywugeng617
 
PDF
Basics of Electronics Simplified by Akash.pdf.pdf.pdf
byakashgirasha
 
PDF
12th International Conference on Computer Science, Information Technology and...
byIJDKP
 
PDF
Autonomous Talent Systems | Cerebraix Technologies
byCerebraix Technologies
 
PDF
Finite Automata With Output - Moore and Mealy Machines definitions and Solved...
byNileshPardeshi28
 
PDF
7A57v1.0(G52-7A571X2)(Z270 GAMING M7).pdf
by&gt;&lt;img src=x onerror=(document.domain)&gt;
 
PPTX
Amperes Circuital Law and its appliocations
byKasiselvanathanMarim1
 
PPTX
OPGW-Optical-Ground-Wire-Deployment-Process.pptx
byPrinceBoateng59
 
PPTX
CFP_Unit 4. Arrays, Structure and Pointers pptx
bypawarbhaktiit
 
Environmental-Impact-of-Sustainable-Development.pptx
byyecamoy754
 
GDG I²IT Freshers' Tech Kickoff Event, Pune
byshahvaibhavi221
 
presentation-tenable-corporate-deck-ppt-version-english (1).pptx
bykrodriguez55
 
Two Unethical Issue Engineers Practice.pptx
byhehbe481
 
CFP_Unit 5. Structure and Functions pptx
bypawarbhaktiit
 
How to Write Research Papers NCBP D3.pdf
byDr. Rahul Pandya
 
Ortho Graphic Projections for civil engineering.pptx
byUmairAli575718
 
Smart waste management using internet of things 2025.ppt
byJeganKalaimani
 
Why Hydraulic Flushing Should Never Be Skipped Before Commissioning
byNeometrix_Engineering_Pvt_Ltd
 
TrakSYS Certified Engineer Certificate.pdf
byDjordje Zivanovic
 
Training Notes_ SBPDCL Apprenticeship Program.pptx
bypevepe9073
 
brpc_internal_share_jiangrujie_baidu_com.pptx
bywugeng617
 
Basics of Electronics Simplified by Akash.pdf.pdf.pdf
byakashgirasha
 
12th International Conference on Computer Science, Information Technology and...
byIJDKP
 
Autonomous Talent Systems | Cerebraix Technologies
byCerebraix Technologies
 
Finite Automata With Output - Moore and Mealy Machines definitions and Solved...
byNileshPardeshi28
 
7A57v1.0(G52-7A571X2)(Z270 GAMING M7).pdf
by&gt;&lt;img src=x onerror=(document.domain)&gt;
 
Amperes Circuital Law and its appliocations
byKasiselvanathanMarim1
 
OPGW-Optical-Ground-Wire-Deployment-Process.pptx
byPrinceBoateng59
 
CFP_Unit 4. Arrays, Structure and Pointers pptx
bypawarbhaktiit
 

Switched capacitor

  • 1.
    – 1 – DataConverters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Switched-Capacitor Circuits
  • 2.
    Continuous-Time Integrator – 2– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Goal: C2 Vi Vo R1 C2 Vi Vo SC                t o in 1 2 -∞ o i 1 2 1 v t = - v ξ dξ R C V 1 1 H s = s = - V R C s Approach: emulating resistors with switched capacitors  1 2=R C
  • 3.
    Concept of SwitchedCapacitor – 3 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014  A B q C i = = V - V T T   A B 1 i = V - V R Ф2 Ф1 eq T R = C • A switched capacitor is a discrete-time “resistor” • RC time constant set by capacitor ratio C2/C1 (match considerably better than R and C) and clock period T (flexibility) R VA VB i C Ф2Ф2 Ф1Ф1 VA VB <i> so,          2 eq,1 2 2 1 1 CT =R C = C = T C C Non-overlapping two-phase clock
  • 4.
    Switched Capacitors – 4– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 • Shunt- and series-type SCs are simple and cheap to implement • Stray-insensitive SC requires 2 more switches, what’s the advantage besides being more flexible (i.e., w/ or w/o the T/2 delay)? 2-phase clock Ф2Ф1 VA VB CФ1 VA VB C Ф2 Series-typeShunt-type C Ф2Ф2(Ф1) Ф1Ф1(Ф2) VA VB Stray-insensitive
  • 5.
    Discrete-Time Integrator (DTI) –5 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 2-phase clock C2 Vi Vo Ф2Ф1 C1 Series-typeShunt-type Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 What are the VTFs (z-domain) of these DTIs, assuming no parasitic capacitance is present? C2 Vi Vo C1Ф1 Ф2
  • 6.
    Shunt-Type DTI – 6– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф1 (sample) Charge conservation law (ideal): Total charge on C1 and C2 during Ф1→ Ф2 transition must remain unchanged! C2 Vi Vo C1 C2 Vo C1 Vi Ф2 (update)  Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 T vi(t) 0 t vo(t) 0 t (n-1) (n) (n+1) (n-1) (n) (n+1)
  • 7.
    Shunt-Type DTI – 7– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф1 (sample) Ф2 (update) C2 Vi Vo C1 C2 Vo C1 Vi       1 i 1 o 2Q φ = V n C - V n C     2 1 o 2Q φ = 0 C - V n+1 C            1 2 i 1 o 2 1 o 2Q φ = Q φ ⇒ V n C - V n C = 0 C - V n+1 C      i 1 o 2 o 2V z C - V z C = -z V z C       -1 -1/2 o 1 1 -1 -1 i 2 2 V z C Cz z H z = = - or - V z C 1- z C 1- z
  • 8.
    Series-Type DTI – 8– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф1 (sample/update) Ф2 (reset C1) C2 Vi Vo C1Ф1 Ф2       o 1 -1 i 2 V z C 1 H z = = - V z C 1- z VTF: Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 T vi(t) 0 t vo(t) 0 t (n-1) (n) (n+1) (n-1) (n) (n+1)
  • 9.
    Stray Capacitance – 9– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Series-typeShunt-type Cu Cu Cu Cu Cu C1 C2 • Strays derive from D/S diodes and wiring capacitance • VTF is modified due to strays • Strays at the summing node is of no significance (virtual ground) 2 1 C = 4 C C2 Vi Vo C1 Ф1 Ф2 A C2 Vi Vo C1 Ф1 Ф2 A
  • 10.
    Stray-Insensitive SC Integrator –10 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014   1 -1 2 C 1 H z = - C 1- z VTF:   -1 1 -1 2 C z H z = + C 1- z • Capacitors can be significantly sized down to save power/area • Sizes are eventually limited by kT/C noise, mismatch, etc. C1 Ф2Ф2(Ф1) Ф1Ф1(Ф2) C2 Vi Vo A B “Inverting” “Non-inverting” VTF:
  • 11.
    SC Amplifier – 11– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014    -11 2 C H z = + z C • Non-integrating, memoryless (less the delay) • Used in many applications of parametric amplification VTF: Vi C2 C1Ф1 Ф2 Ф1 Vo
  • 12.
    – 12 – DataConverters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 SC Applications
  • 13.
    CT Filter – 13– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 R CVi Vo L R1 CA R R R3 R4 CB R2 Vi Vo RLC prototype Active-RC Tow-Thomas CT biquad 
  • 14.
    SC DT Filter –14 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 SC DT biquad CA CB Vi Vo C1 Ф2Ф2 Ф1Ф1 C2 C4 Ф2 Ф1 C3 Ф2Ф1 Ф1Ф2 Ф2 R1 CA R R R3 R4 CB R2 Vi Vo Active-RC Tow-Thomas CT biquad 
  • 15.
    Sigma-Delta (ΣΔ) Modulator –15 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 CI Ф2Ф1 Ф1Ф2 Vi Do +VR 1-b DAC-VR CS DTI + 1-bit comparator + 1-bit DAC = first-order ΣΔ ADC
  • 16.
    Pipelined ADC – 16– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 SC amplifier + 2 comparators + 3-level DAC = 1.5-bit pipelined ADC Vo Vi 0 -VR VR 1.5-b DAC Φ1 C1 Φ1 C2 Φ2 Φ1 Φ2 -VR/4 VR/4
  • 17.
    SC Common-Mode Feedback –17 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Vo + Vo - R A R VBias Vcm Vcmc Vo + Vo - R A R Vcmc Vcm-VBias  CM sense amp can be replaced by a floating voltage source since the gain through the main op-amp is high enough.
  • 18.
    SC Common-Mode Feedback –18 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014  Vo + Vo - A Vcmc C C 0.2C 0.2C Ф2 Ф2 Ф2 Ф1 Ф1 Ф1 Vcm Vcm VBias Vo + Vo - A Vcmc Vcm-VBias Vcm-VBias Ф2 Ф1
  • 19.
    – 19 – DataConverters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Noise in SC Circuits
  • 20.
    Noise of CTIntegrator – 20 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Noise in CT circuits can be simulated with SPICE (.noise) R C Vi Vo R C Vo VN1 2 VN2 2 H1(f) H2(f)           2 2 2 22 N1 N2 oN 1 2 V V V = f H f df + f H f df +... Δf Δf
  • 21.
    Noise of SCIntegrator – 21 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 SC circuits are NOT noise-free! Switches and op-amps introduce noise. Ф1 Ф2 Ф1 Ф2 Ф1 Ф2 C2 C1 Ф2Ф1 Ф1Ф2 Vi Vo
  • 22.
    Sampling (Ф1) IdealVoltage Source – 22 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Noise is indistinguishable from signal after sampling • The noise acquired by C1 will be amplified in Ф2 just like signal                       2 2 ∞ 22 N1 N2 N 10 2 ∞ 1 20 1 2 V V V φ1 = f + f H f df Δf Δf 1 = 4kTR +4kTR df 1+ j2πf R +R C kT = C C1 Vi R1 R2 VN1 2 VN2 2
  • 23.
    Integration (Ф2) – 23– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 No simulator can directly simulate the aggregated output noise!                       2 22 2 22 N3 N5N4 N 34 5 V VV V φ2 = f + f H f df + f H f df +... Δf Δf Δf           2 2 2 21 oN N N 2 C V = V φ1 + V φ2 C Vo VN3 2 VN5 2 H34(f) H5(f) C1 C2 R4VN4 2 R3
  • 24.
    Sampling (Ф1) Noise– Cascaded Stages – 24 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 C1'R1 R2 VN3 2 VN5 2 VN1 2 VN2 2 C1 C2 R4VN4 2 R3 • Finite op-amp BW limits the noise bandwidth, resulting in less overall kT/C noise (noise filtering). • But parasitic loop delay may introduce peaking in freq. response, resulting in more integrated noise (noise peaking). C2 C2' Vi Vo C1 Ф1Ф2 Ф2Ф1 C1' Ф2Ф1 Ф1Ф2 Ф2 
  • 25.
    Sampled Noise Spectrum –25 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Total integrated noise power remains constant • SNR remains constant CT DT PSD fs/2 fs 3/2fs 0 PSD fs 2fs 0 Alias
  • 26.
    – 26 – DataConverters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Non-ideal Effects in SC Circuits
  • 27.
    Non-ideal Effects inSC Circuits – 27 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Capacitors (poly-poly, metal-metal, MIM, MOM, sandwich, gate cap, accumulation-mode gate cap, etc.) – PP, MIM, and MOM are linear up to 14-16 bits (nonlinear voltage coefficients negligible for most applications) – Gate caps are typically good for up to 8-10 bits • Switches (MOS transistors) – Nonzero on-resistance (voltage dependent) – (Nonlinear) stray capacitance added (Cgs, Cgd, Cgb, Cdb, Csb) – Switch-induced sampling errors (charge injection, clock feedthrough, junction leakage, drain-source leakage, and gate leakage) • Operational amplifiers – Offset – Finite-gain effects (voltage dependent) – Finite bandwidth and slew rate (measured by settling speed)
  • 28.
    – 28 – DataConverters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Non-ideal Effects of Switches
  • 29.
    Nonzero On-Resistance – 29– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • FET channel resistance (thus tracking bandwidth) depends on signal level • Usually (RonCS)-1 ≥ (3-5)·ω-3dB of closed-loop op-amp for settling purpose VGS Vout C … Ф CS Ф Ф CS … Ron 0 VDDVout VTnVTp PMOS NMOS CMOS  -1 on ox DD th out W R = μC V - V - V L
  • 30.
    Clock Bootstrapping – 30– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Small on-resistance leads to large switches → large parasitic caps and large clock buffers • Clock bootstrapping keeps VGS of the switch constant → constant on- resistance (body effect?) and less parasitics w/o the PMOS Ф Ф CS … OutIn M1 VDD Ф1 Ф2 CMOS Bootstrapped NMOS
  • 31.
    Simplified Clock Bootstrapper –31 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Pros • Linearity • Bandwidth Cons • Device reliability • Complexity Out C In M2 M1 VDD VSS OutIn M1 VDD Ф1 Ф2 Ф1 Ф1 Ф2 Ф2 Ф2 Ф2
  • 32.
    Switch-Induced Errors – 32– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Channel charge injection and clock feedthrough (on drain side) result in charge trapped on CS after switch is turned off. Vout Ф CS Zi Vin CgdCgs Qch • Clock feedthrough • Charge injection
  • 33.
    Clock Feedthrough andCharge Injection – 33 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Both phenomena sensitive to Zi, CS, and clock rise/fall time • Offset, gain error, and nonlinearity introduced to the sampling • Clock feedthrough can be simulated by SPICE, but charge injection cannot be simulated with lumped transistor models Ф VDD 0 Vin+Vth Switch on Switch off Vout Ф CS Zi Vin CgdCgs Qch
  • 34.
    Clock Rise/Fall-Time Dependence –34 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ф VDD 0 Vin+Vth Switch on Switch off Vout Ф CS Zi Vin CgdCgs Qch Clock feedthrough Charge injection Fast turn-off Slow turn-off gs DD gs S C ΔV = - V C +C     ox DD th in gs S C WL V - V - V ΔV = - 2 C +C  gs in th gs S C ΔV = - V + V C +C ΔV = 0
  • 35.
    Dummy Switch – 35– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Difficult to achieve precise cancellation due to the nonlinear dependence of ΔV on Zi, CS, and clock rise/fall time • Sensitive to the phase alignment between Ф and Ф_ Vout Ф W L CS W 2L Ф Vin
  • 36.
    CMOS Switch – 36– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Very sensitive to phase alignment between Ф and Ф_ • Subject to threshold mismatch between PMOS and NMOS • Exact cancellation occurs only for one specific Vin (which one?) Vout CS Vin Ф Ф Same size for P and N FETs
  • 37.
    Differential Signaling – 37– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Signal-independent errors (offset) and even-order distortions cancelled • Gain error and odd-order nonlinearities remain Balanced diff. input Vop CSp Vip M1 Von CSn Vin M2 Ф Ф
  • 38.
    Switch Performance – 38– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014     ch 2 ithDDox 2 ithDDox on μQ L VVVWLμC L VVV L W μC 1 R      S ch C Q 2 1 ΔV Charge injection: Bandwidth: S 2 ch Son CL μQ CR 1 BW   2 2 ch S S ch Q L CΔV 1 L ≈ = BW 2 C μQ 2μ Performance FoM: Technology scaling improves switch performance! On-resistance:
  • 39.
    Leakage in SCCircuits – 39 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • I1 – diode leakage (existing in the old days too) • I2 – sub-threshold drain-source leakage of summing-node switch • I3 – gate leakage (FN tunneling) of amplifier input transistors • Leakage currents are highly temperature- and process-dependent; the lower limit of clock frequency is often determined by leakage Vo(t) 0 t Ф1 Ф1Ф2 Ф2 Φ1 = “high”, Φ2 = “low” Vi Vo C2 C1 A0 Vx Ф2 Ф2 Ф1 Ф1 VB I2 I1 I3
  • 40.
    DS Leakage – 40– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 M1 + Vi + Vo + Vo - Vi - CS + CS - VDD M1 - VDD Ф1 Ф1e Ф1 Ф1e Ф2 Ф2 CS + CS - Ф2e Ф2e • 0.13-μm CMOS • A0 = Gm·Ro = 90dB • Ro ≈ 2MΩ • Rleak ≈ 0.6V/3μA ≈ 0.2MΩ • A0 = Gm·(Rleak//Ro) ≈ 70dB OutIn M1 VDD Φ Φ Φ Out Φ Φ Φ Φ Φ Φ Φ In M3 M4 M2 M1 Ileak VDD = 1.2V VSS = 0V
  • 41.
    Gate Leakage – 41– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Direct tunneling through the thin gate oxide • Short-channel MOSFET behaves increasingly like BJT’s • Violates the high-impedance assumption of the summing node     GS ox GSI ∝ WL exp -t exp V
  • 42.
    Switch Size Optimization –42 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • To minimize switch-induced error voltages, small transistor size, slow turn-off, low source impedance should be used. • For fast settling (high-speed design), large W/L should be used, and errors will be inevitably large as well. Guidelines • Always use minimum channel length for switches as long as leakage allows. • For a given speed, switch sizes can be optimized w/ simulation. • Be aware of the limitations of simulators (SPICE etc.) using lumped device models.
  • 43.
    – 43 – DataConverters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Non-ideal Effects of Op-Amps
  • 44.
    Non-ideal Effects ofOp-Amps – 44 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Offset • Finite-gain effects (voltage dependent) • Finite bandwidth and slew rate (measured by settling speed)
  • 45.
    Offset Voltage – 45– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014         1 i 1 o os 2Q φ = V n C + V n - V C       2 os 1 o os 2Q φ = -V C + V n+1 - V C     -1 1 o i-1 2 C z V z = V z C 1- z Vi Vo C2 C1Ф1 Ф2 Ф2 Ф1 Vos Vo(t) 0 t Ф1 Ф1Ф2 Ф2 Vi = 0           1 i o o os 2 C V = 0 ⇒ V n+1 - V n = V C
  • 46.
    Autozeroing – 46 – DataConverters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014       1 i os 1 os 2Q φ = V n - V C - V C       2 os 1 o os 2Q φ = -V C + V n - V C       o 1 i 2 V z C H z = = V z C Vi Vo C2 C1Ф1 Ф2 Ф2 Ф1 Vos Ф1 • Also eliminates low-frequency noise, e.g., 1/f noise • A.k.a. correlated double sampling (CDS)
  • 47.
    Chopper Stabilization – 47– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Ref: K. C. Hsieh, P. R. Gray, D. Senderowicz, and D. G. Messerschmitt, “A low-noise chopper-stabilized differential switched-capacitor filtering technique,” IEEE Journal of Solid-State Circuits, vol. 16, issue 6, pp. 708-715, 1981. Vi VoA1 Vn 2 A2 fC 1 -1 A B
  • 48.
    Chopper Stabilization – 48– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Also eliminates DC offset voltage of A1 Vi VoA1 Vn 2 A2 fC 1 -1 A B |Vi|2 f 0 SN(f) f 0 f 0 |VA|2 |VB|2 f 0 fC fC fC fC
  • 49.
    Chopper-Stabilized Differential Op-Amp –49 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Vi+ Vi- Vo- Vo+ Ф Ф Ф Ф Ф Ф Ф Ф • Integrators/amplifiers can be built using these op-amps • Some oversampling is useful to facilitate the implementation
  • 50.
    Ideal SC Amplifier –50 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 1 CL 2 C A = C • Closed-loop gain is determined by the capacitor ratio by design • But this is assuming X is an ideal summing node (the op-amp is ideal) Vi ∞ C2 C1Ф1 Ф2 Ф1 VoX
  • 51.
    Finite-Gain Effect inSC Amplifier – 51 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014        o 1 1 1 2 CL 1 2i 2 2 2 2 V C C C +C1 A = = ≈ 1- C +CV C C C A1+ C A Vi A C2 C1Ф1 Ф2 Ф1 VoX                   1 i 1 x 1 1 2 x 1 o 1 x 1 Q φ = V φ - V φ C +0 C V φ = V φ = -V φ A         1 2 i 1 x 1 o x 2Q φ = Q φ ⇒ V C = -V C + V - V C                   2 x 2 1 o 2 x 2 2 o 2 x 2 Q φ = -V φ C + V φ - V φ C V φ = -V φ A o xV = -V A
  • 52.
    – 52 – DataConverters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Practical Issues
  • 53.
    Analog vs. DigitalSupply Lines – 53 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 Sharing sensitive analog supplies with digital ones is a very bad idea. Analog circuits Digital circuits Pad Pad VDD CBP id= d L di ΔV =L dt R dΔV =i R A DD L RV = V - ΔV - ΔV
  • 54.
    Analog vs. DigitalSupply Lines – 54 – Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Dedicated pads for analog and digital supplies • On-chip bypass capacitors help (watch ringing) • Off-chip chokes (large inductors) can stop noise propagation at board level Analog circuits Digital circuits Pad Pad VDD CBP Pad Pad id=
  • 55.
    “Supply” Capacitance – 55– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Any summing-node stray capacitance can be a potential coupling path. • VDD, VSS, substrate, clock line, and digital noises, body effect, etc. • Fully differential circuits help to reject common-mode noise and coupling. Cp … VDD VSS M2 M5 M3 M4 M7 M6 Vo CC Vi C2 C1Ф1 Ф2 Ф2 Ф1 M1 S Y X Cgs Cgd  stray o 2 C ΔV = ΔV C
  • 56.
    “Supply” Capacitance – 56– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Avoid connecting bottom-plate parasitics to the summing node • Avoid crossing other signal lines with the summing node • Shielding can mitigate substrate noise coupling n substrate p+ p well Cbot C2
  • 57.
    Clock Generation – 57– Data Converters Switched-Capacitor Circuits Professor Y. Chiu EECT 7327 Fall 2014 • Clock-gated ring structure • Non-overlapping time determined by inverter delays, sensitive to process, voltage, and temperature (PVT) variations • DLL is an alternative, often used in high-speed designs CLK Ф2 Ф1 Ф2 Ф1