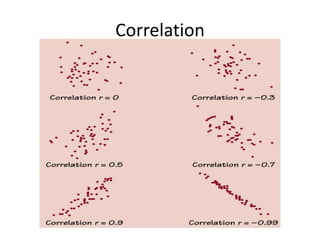
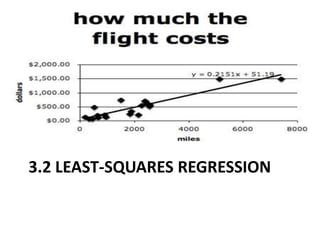
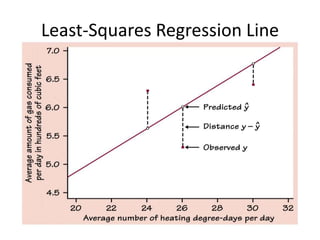
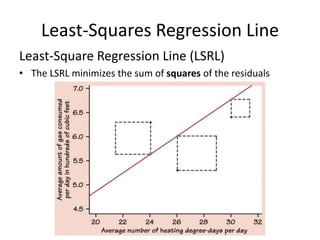
This chapter discusses examining relationships between two quantitative variables using scatterplots and correlation. Scatterplots show the relationship between an explanatory and response variable by plotting each data point. Correlation measures the strength and direction of the linear relationship between two variables on a scale of -1 to 1. The least squares regression line fits a straight line to minimize the residuals, or vertical distances between the data points and the line. It is used to model and make predictions about the relationship between two variables.

1. Chapter 3
Examining Relationships
Examining Relationships

2. 3.1 SCATTERPLOTS AND
CORRELATION

3. Basics
• Up until now, we have been concerned with
“one-variable data”
• We are about to view the relationship
between two-variables.
• Do two variables have to be related?

4. Variables
• Response Variable
– This is the variable that is measured in a study
– The “outcome” of studies
– We can think of it as our “dependant variable”
–(y)

5. Variables
• Explanatory variable
– May (or may not) influence or change the
response variable
– We often would like to show that different values
of explanatory will affect the response
– “independent variable”
–(x)

6. Variables
• More often than not, explanatory v. response
is just a vocabulary choice.
• Just because we are calling a variable the
“response variable” does not mean that the
corresponding “explanatory variable” causes
change!
• We are content right now to just examine if a
relationship exists between the two variables

7. Scatterplots
• Shows the relationship between two quantitative
variables
• Each data pair is represented by a point
• x- coordinate is the value of the explanatory
variable
• y-coordinate is the value of the response variable
• Be sure to label and scale both axes!!
• Quickly automated using the TI!

8. Scatterplots on the TI-84
• [stat], [1] (Edit)
• Enter the explanatory variables in “L1”
• Enter the response variables in “L2”
– Make sure your L1 and L2 correspond
• [2nd], [Y=] (STATPLOT), [1]
– You can define a number of plots from here
• Turn “ON” the plot
• Choose the scatterplot (first icon)
• Xlist: “L1”
• Ylist: “L2”
• [zoom], [9] (zoomstat)
– I recommend starting with this zoom. Examine and take note of the
window!

9. Scatterplots on the TI89
• From the “apps” choose the “stat/list”
• Enter the explanatory variables in “list1”
• Enter the response variables in “list2”
• [F2] (plots),[F1] (define)
• Plot Type: “scatter”
• x: “list1”
• y: “list2”
• [ENTER]
• (Zoomdata)

10. Interpreting a Scatterplot
Use the following list when asked to comment on a
scatterplot/relationship between 2 variables.
1. Direction/Association: is the slope positive or
negative?
2. Form:
1. Linear or nonlinear? If nonlinear, what is the relationship
(more on this later)
2. Are there any clusters? How many?
3. Strength of relationship: strong, moderate, weak?
4. Outliers? Outliers are either outliers in the x-direction,
y-direction, or both

11. Categorical data
• We can add categorical information to a
scatterplot by using multiple marker types
• Example: all marks that represent dogs are a
box, all marks that represent cats are circles
• Sometimes differing patterns will appear
when categorical information is added!

12. 3.1 A
• P173 #1, 4, 5, 7, 9

13. Correlation
• One way to measure the strength of a linear
relationship is to calculate it with variable “r”
• The variable r measures both the strength and
the direction of the relationship
• r is known as the “correlation coefficient” and
measures the quantity “correlation”
• You should not use the word “correlation”
unless you mean r.

14. Correlation
1 xi x yi y
r
n 1 sx sy
• The above formula is quite time consuming!
• We will compute r on a small set of data.
• Thankfully, we can compute r using our TI
(more on this later)
• No.

15. Correlation
• r = 0 indicates “no linear relationship”
• r = 1 indicates “perfect line with positive
slope”
• r = -1 indicates “perfect line with negative
slope”
• Remember -1 < r < 1

16. Correlation

17. Cautions
• Correlation requires both variables to be
quantitative
• Correlation does not described curved
relationships
• Correlation is not resistant- outliers have a
strong effect on r
• Correlation is not a complete summary of
2-variable data

18. Assignment 3.1B
• P188 #13, 16, 19, 20, 23, 24

19. 3.2 LEAST-SQUARES REGRESSION

20. Regression Line
Regression Line
• A line (linear equation) that describes the
relationship between two variables
• Naturally, just calling a line a “regression line”
does not mean that it does an accurate job
describing a relationship!
• If you had done this in an algebra class, you
probably just “eyeballed” a relationship or found
the equation of a line that connected two points
in the scatter.

21. Regression Line
• Regression lines in statistics are a bit “backwards”
from what you learned in algebra!
• a = y-intercept
– This is the predicted value of the response variable
when the exp. var. is zero.
• b = slope
– This is the average amount the resp. var. changes for
every change of one unit in the expl. var.
• You will be asked to interpret both the values of
‘a’ and ‘b’

22. Extrapolation and Interpolation
Interpolation
- Use the regression line to predict values of the
resp var for a expl var within the data range.
Extrapolation
- Use the regression line to predict values of the
resp var for a expl var outside the data range.
- As you might suspect, interpolation good,
extrapolation bad
- OK, not really. You need to use results obtained from
extrapolation with great caution.

23. Least-Squares Regression Line
Least-Square Regression Line (LSRL)
• A good regression line should minimize the
vertical distance between an actual y value of
a point in the scatter and the corresponding y-
value on the regression line.
• This distance (yactual – ypredicted) is known as a
residual.

24. Least-Squares Regression Line

25. Least-Squares Regression Line
Least-Square Regression Line (LSRL)
• The LSRL minimizes the sum of squares of the residuals

26. Least-Squares Regression Line
Computation of the LSRL
1) Obtain xbar, ybar, r, sx and sy
2) Compute ‘b’
3) Compute ‘a’
4) Give the equation of the LSRL
The regression line always goes through (xbar, ybar)
sy
b r
sx
a y bx (this is from y a bx )

27. Least-Squares Regression Line
• The equation of your line should be as follows
 a bx
y
or
resp var a b expl var
• It’s called “y hat”
• In stats, “hats” indicate predicted values
• The example below is an example of the second
notation.
(fat gain) = 3.505 – 0.00344 x (NEA change)

28. Reading a printout

29. Reading a printout
As part of the “great compromise of
1998,” you will be required to
interpret a printout like the one
above

30. Reading a printout
This is the value of ‘a.’ Look for the
line that says constant
a = 1.0891

31. Reading a printout
This is the value of ‘b.’ It is the
coefficient of the line with the
explanatory variable
b = 0.1889

32. Reading a printout
The LSRL for this printout is:
(Gas Used) = 1.08921 + 0.1889 (degree-days)

33. Assignment 3.2A
• P204 #29, 32, 33, 36, 38

34. LSRL on the TI83/84
1. Input data in L1 and L2
2. From home, *stat+, “CALC,” *8+ (LinReg a+bx)
3. On the home screen enter the variable list:
“LinReg L1, L2, Y1”
(this will copy and paste the LSRL into Y1)
AMAZING! It computes “r” for you, too!
4. [zoom], [9] (zoomstat)
Take a good look at your LSRL!

35. LSRL on the TI89
1. On the “stat list” app, input data in “list1” and
“list2”
2. [F4] (calc)
3. Choose LinReg a+bx
4. Select “list1” and for the expl var and list2 resp
var
5. Select “y1” for “store list”
6. [ENTER] and behold the magic!
7. *F2+, “zoom data”

36. Residuals
• (This is where the analysis begins)
• Recall that the residual of a point is y – yhat
(yactual - ypredicted).
• Luckily when you compute an LSRL, your
calculator will automatically compute the
residuals and place them in a list called
“RESID”
– Keep scrolling to the right

37. Residual Plots
• A residual plot is a type of scatter plot where
the x-coordinate is the expl var of an
observation and the y-coordinate is the
residual of the observation.
• Scatter plot of “expl var” vs. “resid”

38. Residual Plots
To create a residual plot on your TI,
1. Create a LSRL for your data
2. Choose a scatterplot from the [stat plot]
menu,
3. Set “Xlist: L1”
4. Set “Ylist: RESID” (*2nd+ ,*stat+,”NAMES”)
5. Turn off all other plots and graphs
6. [ZOOM], [9]

39. Residual Plots
• Residual plots tell us whether a linear model
was a good choice for our data.
• We want the residual plot to look like an
unstructured scatter of points
• The presence of a curve or any other pattern
indicate that the linear model might not be
the best choice.

40. Residual Plots
• A “fan-shaped” pattern (vuvuzela?) indicates
that the linear model only works well for
larger or smaller values of x
• Residuals should be small in value
– Standard deviation of residuals should be small
2
y 
y
s
n 2

41. Assn 3.2B
• P 212 #34, 35, 37, 39, 41

42. Coefficient of determination
• The value of r2 is known as the coefficient of
determination.
2 2
y y y 
y
r2 2
y y
or popularly(?)
2 SST SSE
r
SST

43. Coefficient of determination
• You may often see r2 abbreviated as “R-sq”
• SST = sum of the squares of residuals using the
regression y = ybar.
• SSE = sum of the squares of the residuals
using the LSRL.
• r2 gives us the percentage difference of the
areas of the two regressions
– You can think of the regression y = ybar as the most
basic regression line possible.

44. Coefficient of determination
• Interpretation
• r2 given tells us “(r2) percent of the variation in
(reponse variable) can be explained with a
LSRL relating (response variable) and
(explanatory variable)”
• Fill in the blanks.
• “60.6% of the variation in fat gain is explained
by the least-square regression line relating fat
gain and nonexcercise activity.”

45. Facts about LSRL
• The distinction between expl var and resp var
is essential.
– You will get a different LSRL if you switch variables
• Correlation is closely related to the slope
• The LSRL always passes through (xbar, ybar)
• r2 is the fraction of variation in y that is
explained with a LSRL regression of y on x.

46. 3.3 CORRELATION AND
REGRESSION WISDOM

47. Cautions!
• Correlation and Regression are only useful if
the data shows a linear pattern
• Extrapolation often produces unreliable
predictions
• Correlation is not resistant
– Outliers will affect your regressions!

48. Outliers and Influential Points
• Regression outliers fall outside the overall
pattern of the other observations
– These can be outliers in the x and/or y direction
• Influential points greatly affect the regression
with their inclusion/exclusion
– These are often outliers in the x direction.

49. Lurkers
• Often an unaccounted variable will affect both
the “explanatory” and “response”
– In this scenario, both the “explanatory” and
“response” are actually responding to a third variable!
• EX. When the #of Methodist ministers in New
England increased from 1860-1915, the #of
barrels of imported Cuban rum also increased
with a r = 0.999! Would we say that the #of
Methodist ministers causes an increase in import
of Cuban rum?

50. Remember
• Association does not imply causation!

51. Chapter 3 REV
• P 228 #46, 55, 62, 70, 77, 80, 83, 84