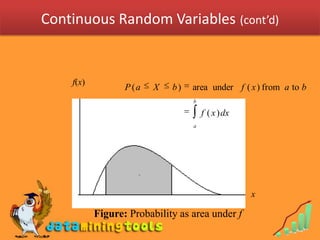
1. Continuous random variables are defined over intervals rather than discrete points. The probability that a continuous random variable takes on a value in an interval from a to b is given by an integral of the probability density function f(x) over that interval. 2. The probability density function f(x) defines the probabilities of intervals of the continuous random variable rather than individual points. It has the properties that it is always nonnegative and its integral over all values is 1. 3. The cumulative distribution function F(x) gives the probability that the random variable takes on a value less than or equal to x. It is defined as the integral of the probability density function from negative infinity to x.

1. 1.7 Continuous Random Variables

2. Continuous Random Variables Suppose we are interested in the probability that a given random variable will take on a value on the interval from a to b where a and b are constants with a  b. First, we divide the interval from a to b into n equal subintervals of width x containing respectively the points x1, x2, … , xn. Suppose that the probability that the random variable will take on a value in subinterval containing xi is given by f(xi)x. Then the probability that the random variable will take on a value in the interval from a to b is given by

3. Continuous Random Variables(cont’d) If f is an integrable function defined for all values of the random variable, the probability that the value of the random variables falls between a and b is defined by letting x  0 as Note: The value of f(x) does not give the probability that the corresponding random variable takes on the values x; in the continuous case, probabilities are given by integrals not by the values f(x).

4. Continuous Random Variables(cont’d) f(x) P(a  X  b) a b x Figure: Probability as area under f

5. Continuous Random Variables(cont’d) The probability that a random variable takes on value x, i.e. Thus, in the continuous case probabilities associated with individual points are always zero. Consequently,

6. Continuous Random Variables(cont’d) The function f is called probability density function or simply probability density. Characteristics of the probability density function f : 1. for all x. 2. F(x) represents the probability that a random variable with probability density f(x) takes on a value less than or equal to x and the corresponding function F is called the cumulative distribution function or simply distribution function of the random variable X.

7. Continuous Random Variables(cont’d) Thus, for any value x, F (x) = P(X  x) is the area under the probability density function over the interval - to x. Mathematically, The probability that the random variable will take on a value on the interval from a to b is given by P(a  X  b) = F (b) - F (a)

8. Continuous Random Variables(cont’d) According to the fundamental theorem of integral calculus it follows that wherever this derivative exists. F is non-decreasing function, F(-) = 0 and F() = 1. kth moment about the origin

9. Continuous Random Variables(cont’d) Mean of a probability density: kth moment about the mean:

10. Continuous Random Variables(cont’d) Variance of a probability density  is referred to as the standard deviation