1. The document defines discrete random variables as random variables that can take on a finite or countable number of values. It provides an example of a discrete random variable being the number of heads from 4 coin tosses. 2. It introduces the probability mass function (pmf) as a function that gives the probability of a discrete random variable taking on a particular value. The pmf must be greater than or equal to 0 and sum to 1. 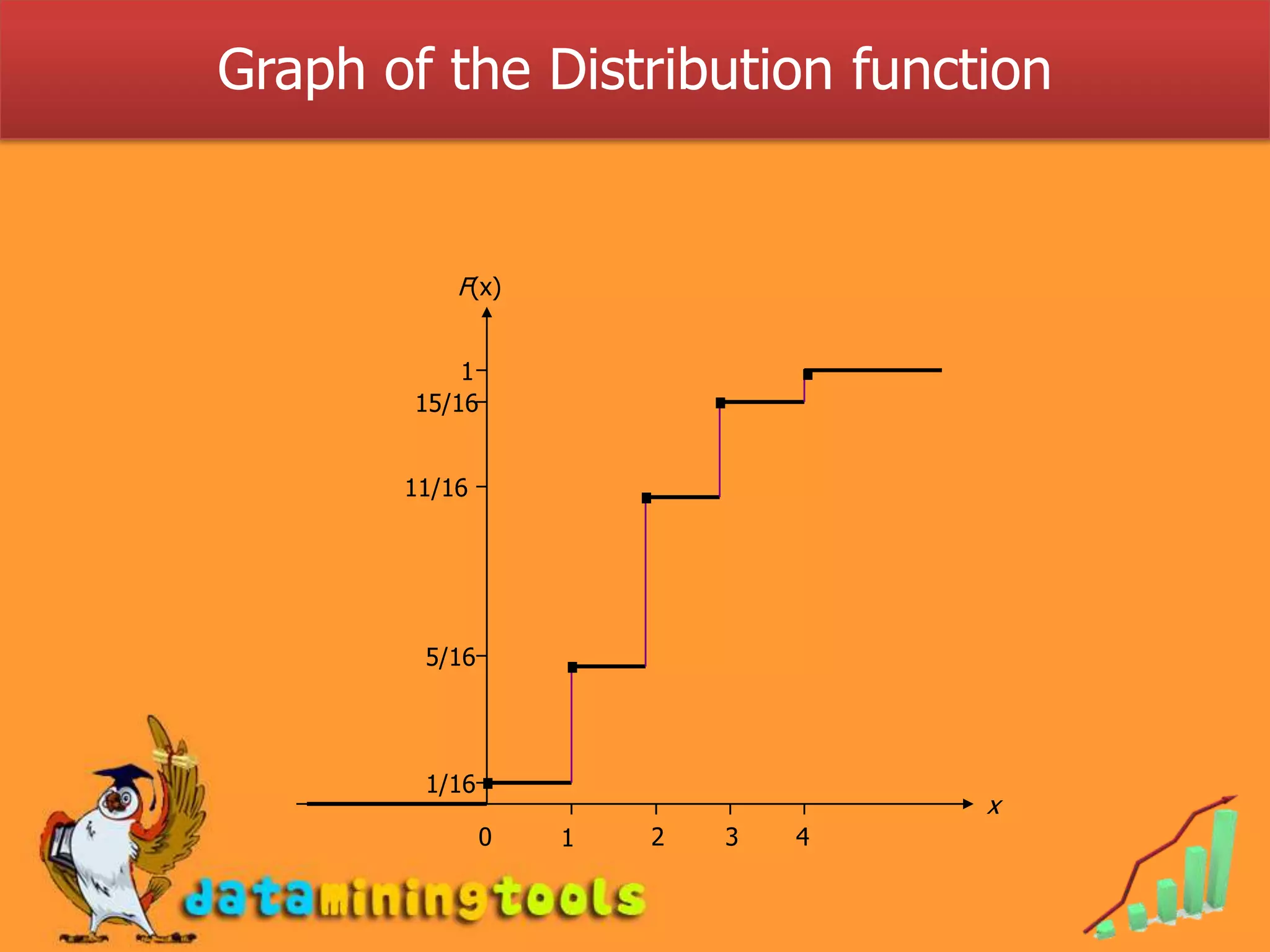3. The cumulative distribution function (CDF) of a discrete random variable is defined as the sum of the probabilities of the random variable being less than or equal to a particular value. The CDF ranges from 0 to 1 and increases monotonically.

1. 1.4 Discrete Random Variables and Probability Distributions

2. Random VariablesDefinition: A random variable X on a sample space S is a rule that assigns a numerical value to each outcome of S or in other words a function from S into the set R of real numbers.X : S  Rx : value of random variable XRX : The set of numbers assigned by random variable X, i.e. range space.

3. Random Variables Classifications of Random Variables According to the number of values which they can assume, i.e. number of elements in Rx.Discrete Random Variables: Random variables which can take on only a finite number, or a countable infinity of values, i.e. Rx is finite or countable infinity.Continuous Random Variables: When the range space Rx is a continuum of numbers. For example an interval or the union of the intervals.

4. Random Variables Example: Consider the experiment consisting of 4 tosses of a coin then sample space isS = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTTH, TTHH, THTH, HTHT, THHT, TTTH, TTHT, THTT, HTTT, TTTT}Let X assign to each (sample) point in S the total number of heads that occurs. Then X is a random variable with range space RX = {0, 1, 2, 3, 4} Since range space is finite, X is a discrete random variable

5. Random Variables Example: A point P is chosen at random in a circle C with radius r. Let X be the distance of the point from the center of the circle. Then X is a (continuous) random variables with RX = [0, r]PCrXO

6. Probability DistributionsIf X is discrete random variable, the function given by f(x) = P[X = x] for each x within the range of X is called the probability mass function (pmf) of X.To express the probability mass function, we give a table that exhibits the correspondence between the values of random variable and the associated probabilities

7. Probability Distributions Ex: In the experiment consisting of four tosses of a coin, assume that all 16 outcomes are equally likely then probability mass function for the total number of heads is

8. Probability Distributions A function can serve as the probability mass function of a discrete random variable X if and only if its value, f(x), satisfy the conditions1. f(x)  0 for all value of x. 2.Example: Check whether the following can define probability distributions

9. Probability Distributions Ans: (a) Yes, (b) No, (c) Yes, (d) No

10. Distribution FunctionIf X is a discrete random variable, the function given bywhere f(t) is the value of the probability mass functionof X at t, is called the distribution function or thecumulative distribution function (cdf) of X.

11. ExampleDistribution function of the total number of heads obtained in four tosses of a balanced coinWe know that f(0) = 1/16, f(1) = 4/16, f(2) = 6/16, f(3) = 4/16, f(4) = 1/16. It follows thatF(0) = f(0) = 1/16 F(1) = f(0) + f(1) = 5/16F(2) = f(0) + f(1) + f(2) =11/16F(3) = f(0) + f(1) + f(2) + f(3) = 15/16F(4) = f(0) + f(1) + f(2) + f(3) + f (4) = 1

12. The distribution function is given by

13. F(x)..115/16.11/16.5/16.1/16x23401Graph of the Distribution function

14. Distribution Function The distribution function is defined not only for the values taken on by the given random variable, but for all real number. We can write F(1.7) = 5/16 and F(100) = 1, although the probability of getting “at most 1.7 heads” or “at most 100 heads” in four tosses of a balanced coin may not be of any real significance.

15. Distribution Function The values F(x) of the distribution function of a discrete random variable X satisfy the conditionsF(-) = 0 and F() = 1; that is, it ranges from 0 to 1.If a < b, then F(a)  F(b) for any real numbers a and b. Hence it is non-decreasing.If the range of a random variable X consists of the values x1 f (xi) = F(xi) - F(xi-1) for i = 2, 3, …, n. That is, f (xi) is the size of the jump in the graph,