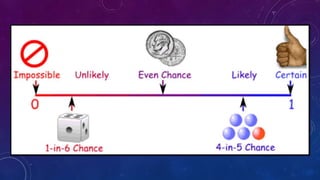
Probability is the chance that something will happen or the likelihood of an event. It is measured by the number of favorable outcomes divided by the total number of possible outcomes. Some key contributors to the development of probability include Buffon, Kerrich, and Pearson who performed coin toss experiments to determine experimental probabilities. Probability is used in various real-life domains like weather forecasting, insurance policies, sports strategies, and medical decisions.

1. PROBABILITY
SLIDE PRESENTATION MADE BY :
SANIKA RAHUL SAVDEKAR

2. “A pinch of probability is
worth a pound of
perhaps.”
- James Thurber

3. Probability is the chance that something will
happen, how likely is that some event will happen.
Sometimes we measure probability in numbers like
10%. Sometimes we use words such as impossible,
unlikely, possible, even chance, likely, certain.
For example: ‘It is likely to rain today.’
‘ I will certainly fail my math test.’

5. HISTORY:
Though it is not known who exactly discovered probability, the following three scientists have
contributed a major part to what we know of probability today-
- The eighteenth century French naturalist Comte de Buffon tossed a coin 4040 times and got
2048 heads. The experimental probability of getting heads in this case was 2048/4040
- J.E. Kerrich from Britain, recorded 5067 heads in 10,000 tosses of a coin. The experimental
probability of getting a head in this case, was 5067/10000= 0.5067
- Statistician Karl Pearson spent some more time, making twenty four thousand tosses of a coin.
He got 12012 heads, and thus, the experimental probability of a head obtained by him was
0.5005.

6. Random Experiment:
In an experiment where all possible outcomes are known and
in advance if the exact outcome cannot be predicted, is called
a random experiment.
Trial:
By a trial, we mean performing a random experiment.
For example; throwing a die or tossing a coin etc.

7. Sample Space:
The total number of outcomes forms a set called Sample Space. n(S) gives total
number of elements in the Sample Space.
Let’s consider few examples:
1. Tossing a coin : Sample space = { H , T }, n(S) = 2
2. Throwing a dice : Sample Space = {1, 2, 3 , 4 , 5 , 6}, n(S) = 6
3. Tossing two coins : Sample Space = { HH, HT, TH, TT}
4. Throwing two dice together = { (1, 1) , (1, 2) , (1, 3) , (1, 4) , (1, 5) , (1, 6)
(2, 1) , (2, 2) , ………..
:
:
:
(6, 1) , ………………………………………., (6, 6)}, n(S) = 36

8. Event:
In probability theory, an event is a set of outcomes of
an experiment (a subset of the sample space) to
which a probability is assigned. Event can be denoted
by any uppercase alphabet.

9. Probability of any event A is given by:
P(A) =
𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑓𝑎𝑣𝑜𝑢𝑟𝑎𝑏𝑙𝑒 𝑜𝑢𝑡𝑐𝑜𝑚𝑒𝑠
𝑇𝑜𝑡𝑎𝑙 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑂𝑢𝑡𝑐𝑜𝑚𝑒𝑠

10. REAL-LIFE PROBABILITY EXAMPLES

11. WEATHER- FORECASTING
• Should we go on a picnic? Is the weather right for travelling? Are the rains going to fare me
well?
All these are questions that probability decides for us.
• If we're looking for the chance it will rain, this will be the number of days in our database that
it rained divided by the total number of similar days in our database. If our meteorologist has
data for 100 days with similar weather conditions (the sample space and therefore the
denominator of our fraction), and on 70 of these days it rained (a favorable outcome), the
probability of rain on the next similar day is 70/100 or 70%.
Since a 50% probability means that an event is as likely to occur as not, 70%, which is greater
than 50%, means that it is more likely to rain than not. But what is the probability that it
won't rain? Remember that because the favorable outcomes represent all the possible ways
that an event can occur, the sum of the various probabilities must equal 1 or 100%, so 100% -
70% = 30%, and the probability that it won't rain is 30%.

12. INSURANCE/ POLICIES
• Probability plays an important role in analyzing insurance policies to determine which plans
are best for you or your family and what deductible amounts you need.
• When choosing a car insurance policy, you use probability to determine how likely it is that
you'll need to file a claim.
• For example, if 12 out of every 100 drivers - or 12 percent of drivers - in your community
have had a ram into electric poles over the past year, you'll likely want to consider
comprehensive - not just liability - insurance on your car. You might also consider a lower
deductible if average car repairs after a electric-pole-related incident and you don't have out-
of-pocket funds to cover those expenses.

13. SPORTS STRATEGIES
• Athletes and coaches use probability to determine the best sports strategies for games and
competitions.
• A baseball coach evaluates a player's batting average when placing him in the lineup. For
example, a player with a 200 batting average means he's gotten a base hit two out of every 10
at bats. A player with a 400 batting average is even more likely to get a hit -- four base hits out
of every 10 at bats.
• If a high-school football kicker makes nine out of 15 field goal attempts from over 40 yards
during the season, he has a 60 percent chance of scoring on his next field goal attempt from
that distance. The equation is:
9 / 15 = 0.60 or 60 percent

14. MEDICAL DECISIONS
• Getting a surgery today, do you think I’ll make it out alive?
• When a patient is advised to undergo surgery, they often want to know the success rate of the
operation which is nothing but a probability rate. Based on the same the patient takes a
decision whether or not to go ahead with the same.
• For example, when a patient with heart issues is asked to get a stent, he/she will ask for the
success rate of the same procedure. Let us take the total amount of stent surgeries performed
by this particular surgeon to be 100. Out of these, 68 have been successful so far whereas 32
have resulted in mishaps. This means that there is a 68/100 = 17/25 chance of you surviving
the operation. However, there is also a 32/100 = 8/25 chance of dying. Thus, probability often
decides our medical actions.

15. The theory of probability is the only
mathematical tool available to help map the
unknown and uncontrollable. It is fortunate
that this tool, though tricky, is extraordinarily
powerful and convenient.
-Benoit Mandelbrot
THANK YOU.

16. BIBLIOGRAPHY
• http://www.ehow.com/list_7719506_real-life-probability-examples.html
• http://mathforum.org/dr.math/faq/faq.prob.world.html
• http://itfeature.com/tag/real-life-examples-probability
• http://www.math-only-math.com/probability.html
• www.Wikipedia.org/probability
• www.meritnation.org/probability