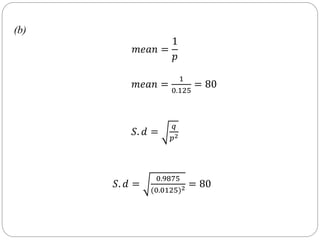
1. A geometric experiment involves independent trials with two possible outcomes (success/failure), where the probability of success (p) is constant across trials. 2. The geometric random variable (X) represents the number of trials until the first success. It has a geometric distribution where P(X=x) = p(1-p)^(x-1). 3. Examples are provided to illustrate calculating the probability of success on a given trial (x), as well as the mean and standard deviation, for geometric distributions with different probabilities of success (p).

1. NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS
GEOMETRIC PROBABILITY
DISTRIBUTION

2. Geometric Experiment:
A Geometric experiment is a random experiment that has
the following properties:
1-Each trial can result in just two possible outcomes. We
call one of these outcomes a success and the other, a
failure.
2-The probability of success, denoted by p, is the same on
every trial.
3-The trials are independent; that is, the outcome on one
trial does not affect the outcome on other trials.
4- number of independent trials until the first success.

3. Geometric Random Variable:
In a geometric experiment, define the discrete random
variable X as the number of independent trials until the
first success.
Geometric Distribution:
We say that X has a geometric distribution and write
X∼g(p)
𝑃 𝑋 = 𝑥 = 𝑝𝑞 𝑥−1 , for x = 1, 2, 3, …….
where p is the probability of success in a single trial.

4. Example-1
The probability of a defective steel rod is 0.01. Steel rods
are selected at random. Find the probability that the first
defect occurs on the ninth steel rod.
Solution:
P = 0.01
q = 1- 0.01 = 0.99
x = 9
𝑃 𝑋 = 𝑥 = 𝑝𝑞 𝑥−1
𝑃 𝑋 = 9 = (0.01)(0.99)9−1
𝑃 𝑋 = 9 = 0.0092

5. Example-2
The lifetime risk of developing lung cancer is about 1.25%.
(a) What is the probability of that you ask ten people before one
says he or she has lung cancer?
(b) Find the (i) mean and (ii) standard deviation.
Solution:
(a) P = 0.0125
q = 1- 0.01 = 0.9875
x=10
𝑃 𝑋 = 𝑥 = 𝑝𝑞 𝑥−1
𝑃 𝑋 = 10 = (0.0125)(0.9875)10−1
𝑃 𝑋 = 𝑥 = 0.0112

6. (b)
𝑚𝑒𝑎𝑛 =
1
𝑝
𝑚𝑒𝑎𝑛 =
1
0.125
= 80
𝑆. 𝑑 =
𝑞
𝑝2
𝑆. 𝑑 =
0.9875
(0.0125)2 = 80

7. Example-3
The literacy rate for a nation measures the proportion of people age 15
and over who can read and write. The literacy rate for women in
Pakistan is 45%. Let X= the number of Pakistani women you ask until
one says that she is literate.
(a) What is the probability distribution of X?
(b) What is the probability that you ask five women before one
says she is literate?
Solution
(a) X∼g(0.45)
(b) P = 0.45 ; q = 1- 0.45 = 0.55 ; x = 5
𝑃 𝑋 = 𝑥 = 𝑝𝑞 𝑥−1
𝑃 𝑋 = 5 = (0.45)(0.55)5−1
𝑃 𝑋 = 𝑥 = 0.0412

8. Example-4
If the probability that a target is destroyed on any one shot
is 0.75, What is the probability that it would be destroyed
on 3rd attempt.
Solution:
P = 0.75
q = 1- 0.75 = 0.25
x = 3
𝑃 𝑋 = 𝑥 = 𝑝𝑞 𝑥−1
𝑃 𝑋 = 3 = (0.75)(0.25)3−1
𝑃 𝑋 = 3 = 0.0469