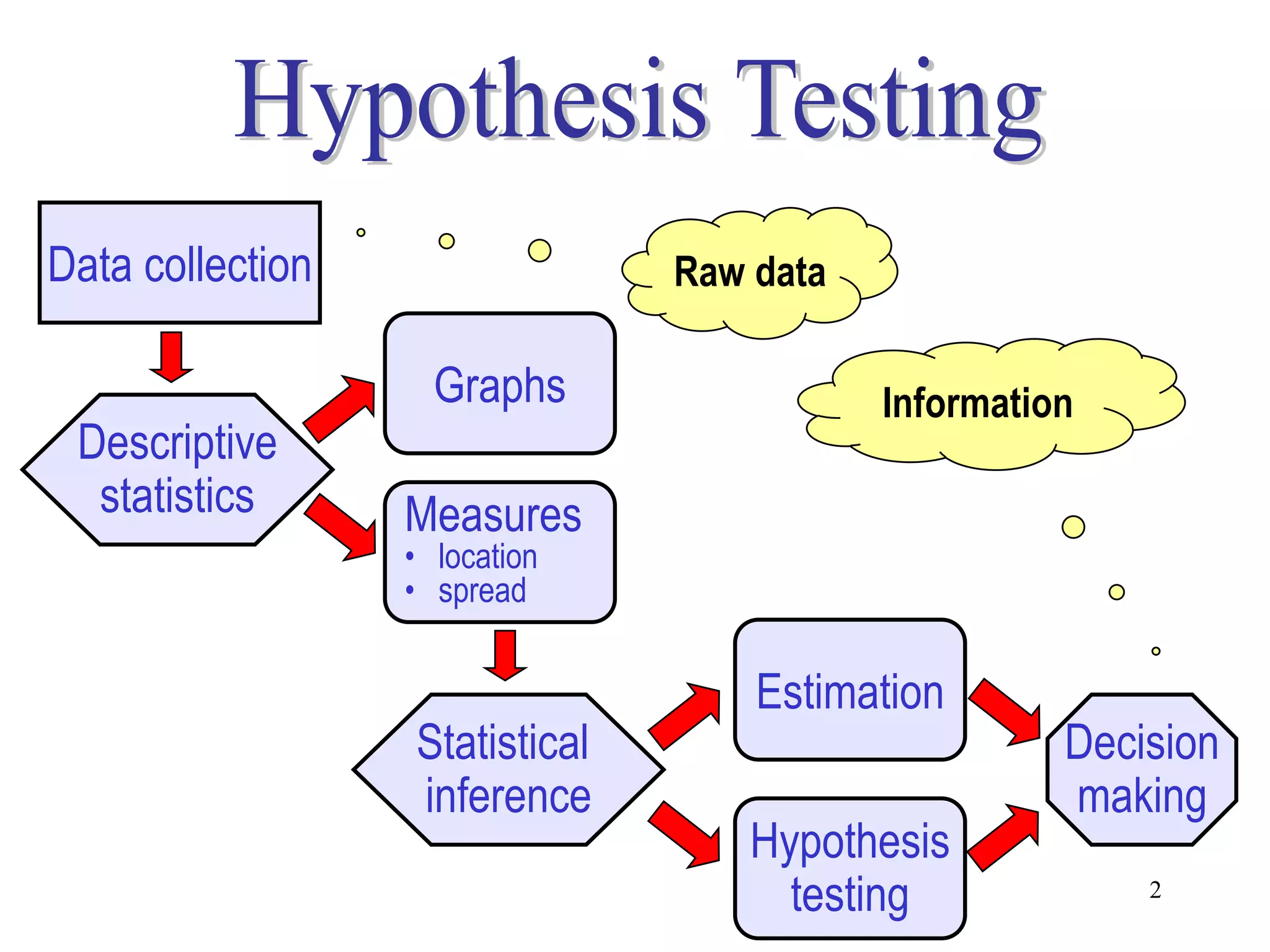
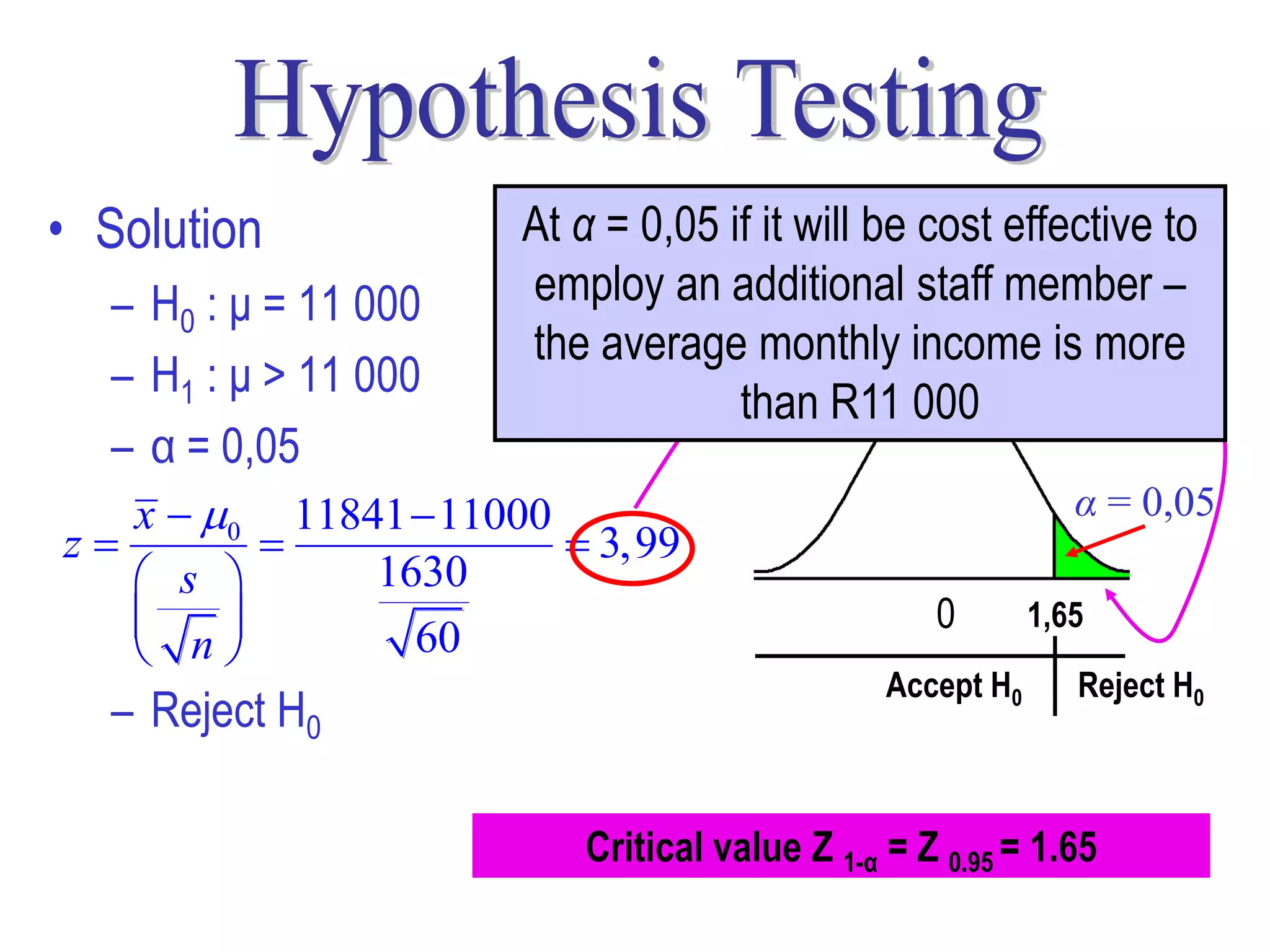
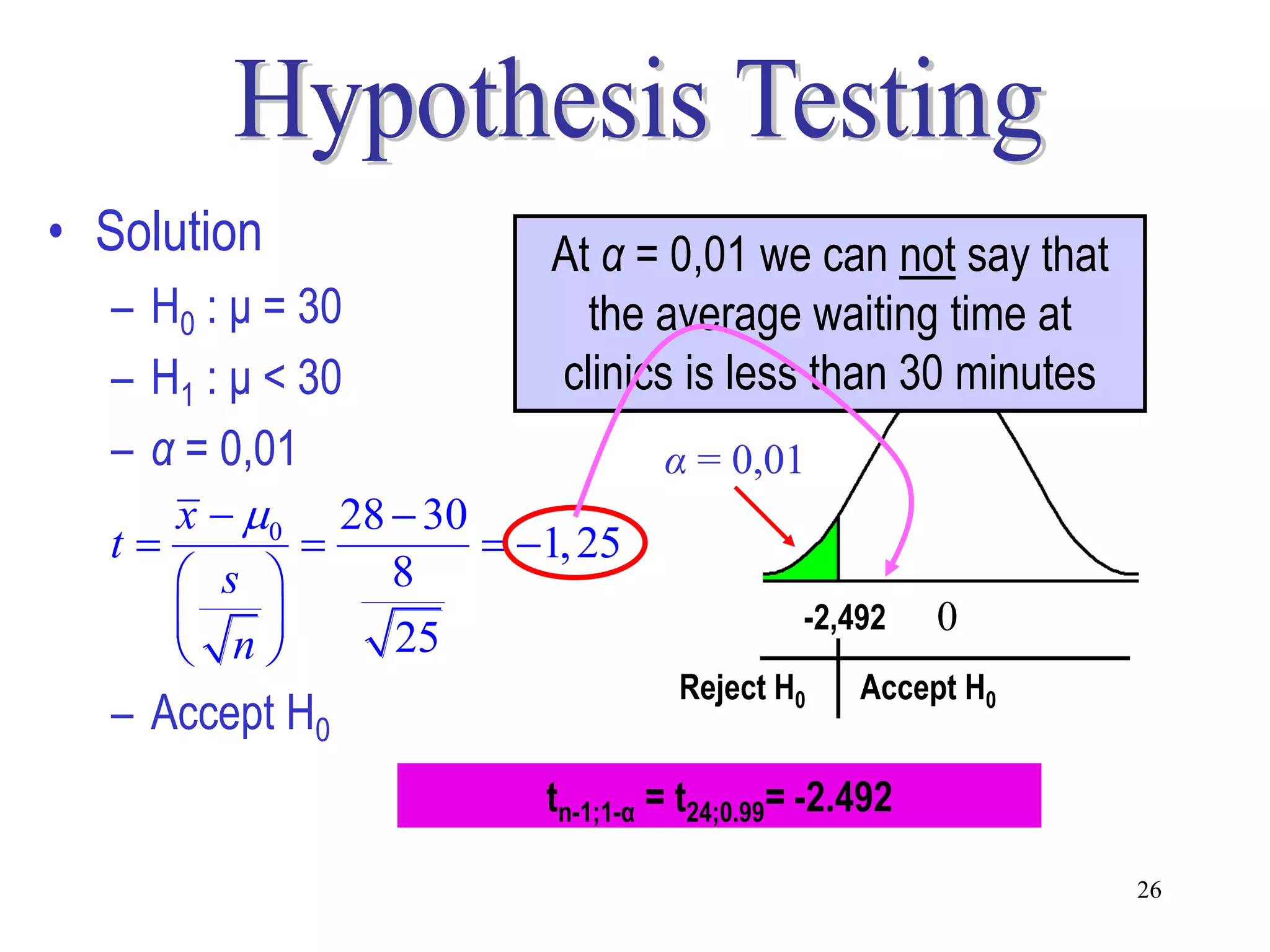
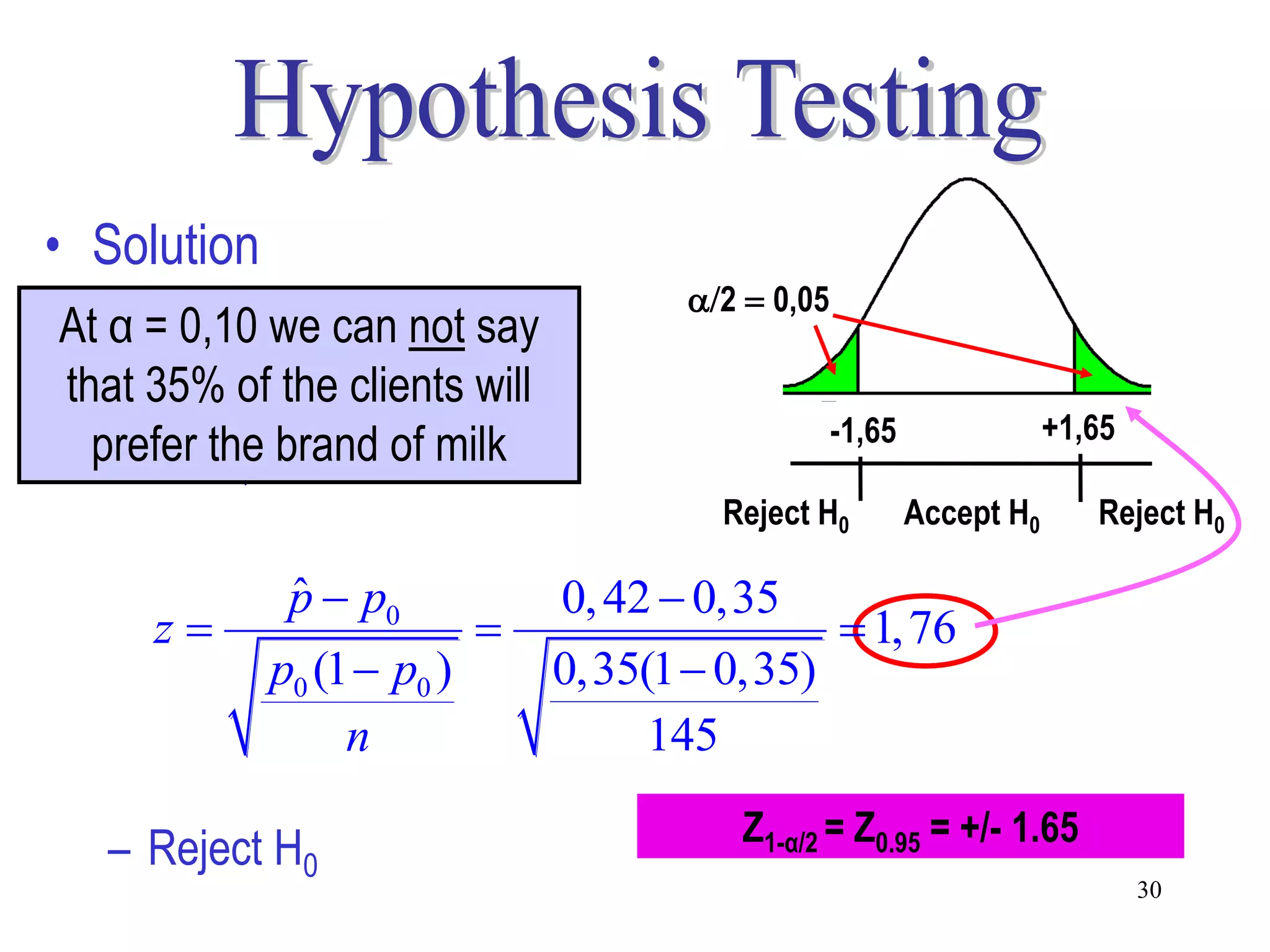
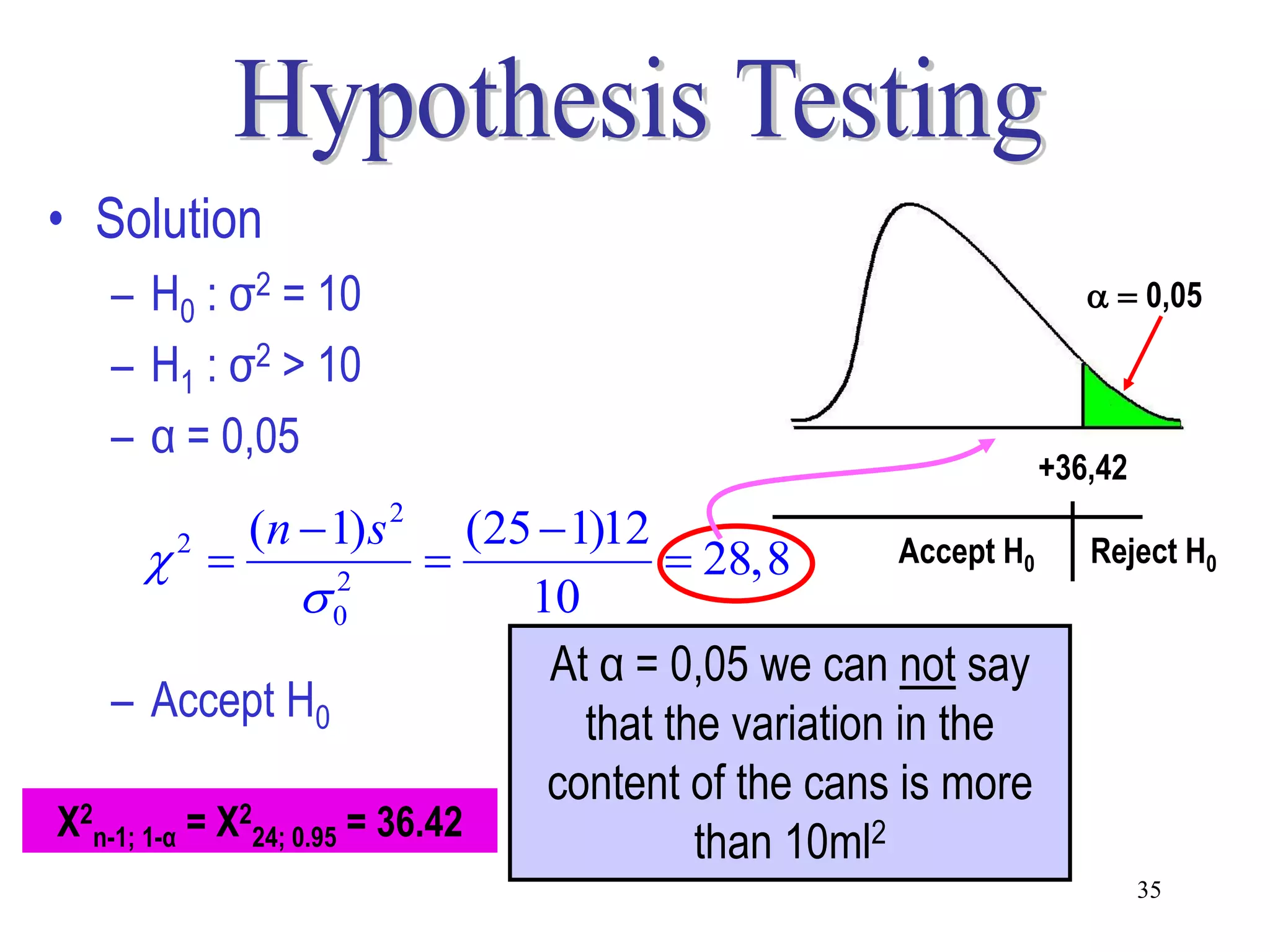
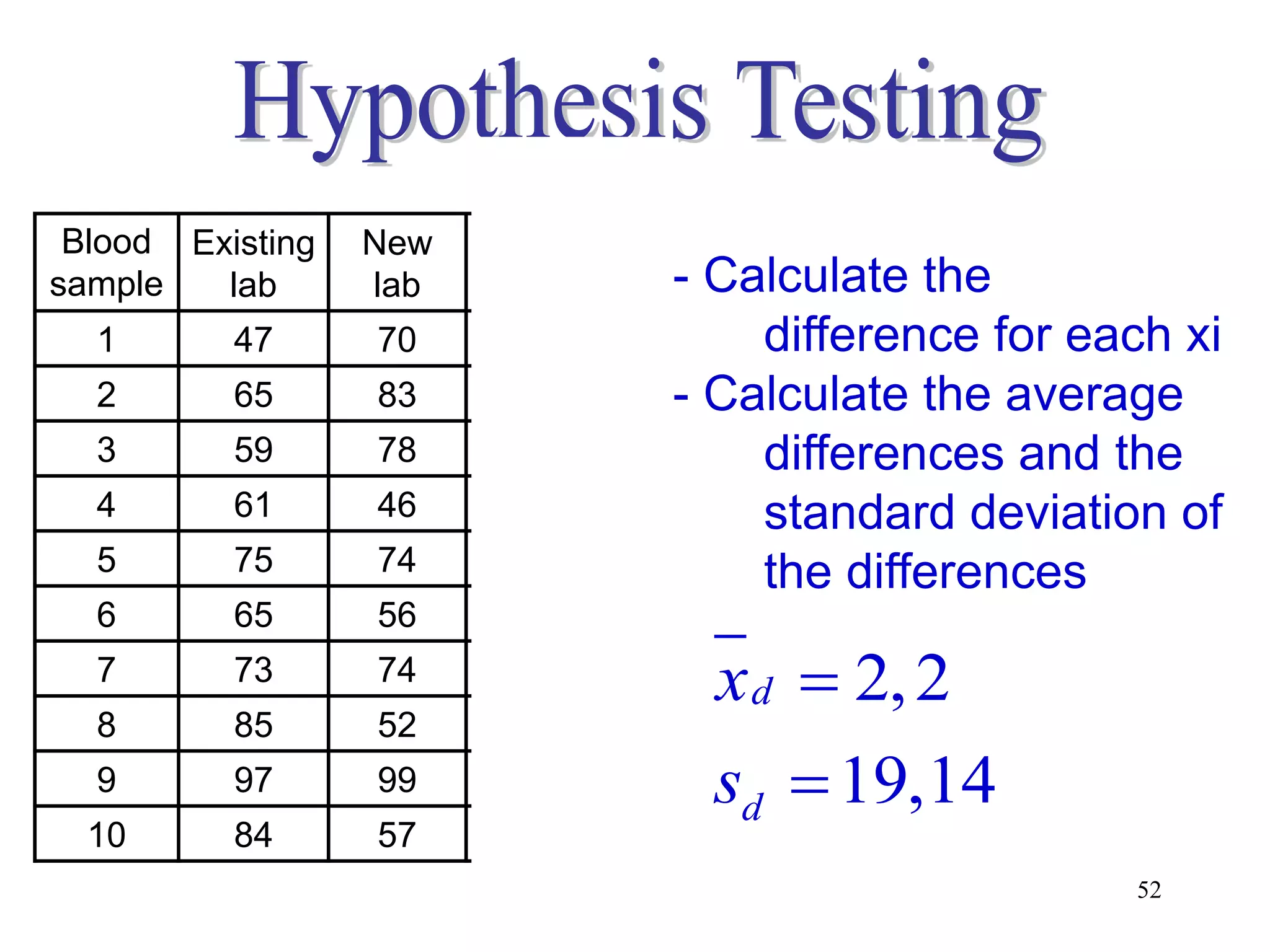
This document discusses hypothesis testing, which is a statistical procedure used to make inferences about populations based on sample data. It involves 6 steps: 1) stating the null and alternative hypotheses, 2) stating the significance level, 3) calculating the test statistic, 4) determining the critical value, 5) making a decision to reject or fail to reject the null hypothesis, and 6) drawing a conclusion. The key concepts covered are the null and alternative hypotheses, types of errors, significance levels, test statistics, critical values, and decision rules for one-tailed and two-tailed hypothesis tests concerning population means and proportions. Examples are provided to illustrate the application of hypothesis testing.

1. 1

2. Data collection Raw data
Graphs Information
Descriptive
statistics Measures
• location
• spread
Estimation
Statistical Decision
inference making
Hypothesis
testing 2

3. • Hypothesis testing is a procedure for
making inferences about a population
• A hypothesis test gives the opportunity
to test whether a change has occurred
or a real difference exists

4. • A hypothesis is a statement or claim that
something is true
H0 always contains = sign
– Null hypothesis H0
• No effect or no difference
• Must be declared true/false
– Alternative hypothesis H1
• True if H0 found to be false
– If H0 is false – reject H0 and accept H1
– If H0 is true – accept H0 and reject H1

5. • State the null and alternative hypotheses that would be used to test each
of the following statements:-
• A manufacturer claims that the average life of a transistor is at least 1000
hours (h)
H0: µ = 1000
H1: µ > 1000
• A pharmaceutical firm maintains that the average time for a certain drug
to take effect is 15 mins
H0: µ = 15
H1: µ ≠ 15
• The mean starting salary of graduates is higher than R50000 per annum
H0: µ = 50000
H1: µ > 50000

6. • Hypothesis testing consists of 6 steps:
1. State the hypothesis
2. State the value of α
3. Calculate the test statistic
4. Determine the critical value
5. Make a decision
6. Draw conclusion
6

7. Hypothesis Testing Step 1 One/Two populations
State the hypothesis Two tailed
H0: parameter = ?
H1: parameter ≠ ?
Ho – Null hypothesis
Right tailed
H1 – Alternative Hypothesis H0: parameter = ?
H1: parameter > ?
Left tailed
H0: parameter = ?
H1: parameter < ? 7

8. Hypothesis Testing Step 2
State the value of α Decision Actual situation
H0 is true H0 is false
Do not Correct
reject H0 decision
Correct
Reject H0
decision
8

9. Hypothesis Testing Step 2
State the value of α Decision Actual situation
H0 is true H0 is false
Two types of errors:
Do not Correct Type II error =
reject H0 decision 
Type I error Correct
Reject H0
= decision
α - Probability of Type I error
Level of significance
1%, 5%, 10%
Determine critical value/s 9

10. LEVEL OF SIGNIFICANCE
• Probability (α) of committing a type I
error is called the LEVEL OF
SIGNIFICANCE
• α is specified before the test is
performed
• You can control the Type I error by
deciding, before the test is performed,
what risk level you are willing to take in
rejecting H0 when it is in fact true
• Researchers usually select α levels of
0.05 or smaller
10

11. Hypothesis Testing Step 3
Calculate value of test statistic
There are different test statistics for testing:
• Single population
– Mean, proportion, variance
• Difference between two population
– Means, proportions, variances
11

12. REJECTION AND NON-REJECTION REGIONS
• To decide whether H0 will be rejected or not , a
value, called the TEST STATISTIC has to be
calculated by using certain sample results
• Distribution of test statistic often follows a normal
or t distribution.
• Distribution can be divided into 2 regions:-
– A region of rejection
– A region of non- rejection
12

13. Hypothesis Testing Step 4
Determine the critical value/values
Right tailed Two tailed Left tailed
H1: parameter > ? H1: parameter ≠ ? H1: parameter < ?
H0 H0 H0
α α/2 α/2 α
- Critical value – from tables 13

14. Hypothesis Testing Step 5
Make decision
Right tailed Two tailed Left tailed
H1: parameter > ? H1: parameter ≠ ? H1: parameter < ?
H0
H0 H0
α α/2 α/2 α
Accept Rej Rej Accept Rej Rej Accept
H0 H0 H0 H0 H0 H0 H0
14

15. Hypothesis Testing Step 6
Draw conclusion
Accept H0
?
H0
Reject H0
?? ?
Test statistic 15

16. STEPS OF A HYPOTHESIS TEST
Step 1 • State the null and alternative hypotheses
Step 2 • State the values of α
Step 3 • Calculate the value of the test statistic
Step 4 • Determine the critical value
Step 5 • Make a decision using decision rule or graph
Step 6 • Draw a conclusion
16

17. Concept Questions
• 1 – 12 page 261 textbook
17

18. Hypothesis test for Population Mean, n ≥ 30
- population need not be normally distributed
- sample will be approximately normal
Testing H0: μ = μ0 for n ≥ 30
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
H1: μ ≠ μ0 |z| ≥ Z1- α/2 x  0
z
H1: μ > μ0 z ≥ Z1- α  s 
 
H1: μ < μ0 z ≤ -Z1- α  n 18
Use σ if known

19. • Example
– It will be cost effective to employee an additional staff
member at a well known take away restaurant if the
average sales for a day is more than R11 000 per day.
– A sample of 60 days were selected and the average sales
for the 60 days were R11 841 with a standard deviation of
R1 630.
– Test if it will be cost effective to employ an additional staff
member.
– Assume a normal distributed population. Use α = 0,05.

20. • Solution
– The population of interest is the daily sales
– We want to show that the average sales is more than
R11 000 per day.
– H1 : μ > 11 000
– The null hypothesis must specify a single value of the
parameter 
– H0 : μ = 11 000
– Need to test if R11 841( x ) is significant more than
R11 000(μ)

21. • Solution At α = 0,05 if it will be cost effective to
– H0 : μ = 11 000 employ an additional staff member –
the average monthly income is more
– H1 : μ > 11 000
than R11 000
– α = 0,05
x  0 11841  11000 α = 0,05
z   3,99
– s  1630
  0 z1-α
1,65
 n 60
Accept H0 Reject H0
– Reject H0
Critical value Z 1-α = Z 0.95 = 1.65

22. • Hypothesis test for Population Mean, n < 30
– If σ is unknown we use s to estimate σ
– We need to replace the normal distribution with the
t-distribution with (n - 1) degrees of freedom
Testing H0: μ = μ0 for n < 30
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
H1: μ ≠ μ0 |t| ≥ tn - 1;1- α/2 x  0
t
H1: μ > μ0 t ≥ tn-1;1- α  s 
 
 n
H1: μ < μ0 t ≤ -tn-1;1- α 22

23. Concept Questions
Questions 13 – 19, page 267, textbook
23

24. • Example
– Health care is a major issue world wide. One of the
concerns is the waiting time for patients at clinics.
– Government claims that patients will wait less than 30
minutes on average to see a doctor.
– A random sample of 25 patients revealed that their average
waiting time was 28 minutes with a standard deviation of 8
minutes.
– On a 1% level of significance can we say that the claim
from government is correct?
24

25. • Solution
– The population of interest is the waiting time at clinics
– Want to test the claim that the waiting time is less than 30
minutes
– H1 : μ < 30
– The null hypothesis must specify a single value of the
parameter 
– H0 : μ = 30
– Need to test if 28( x ) is significant less than 30(μ)
25

26. • Solution At α = 0,01 we can not say that
– H0 : μ = 30 the average waiting time at
– H1 : μ < 30 clinics is less than 30 minutes
– α = 0,01 α = 0,01
x  0 28  30
t   1, 25
–  s  8
  -t1-α
-2,492 0
 n 25
Reject H0 Accept H0
– Accept H0
tn-1;1-α = t24;0.99= -2.492
26

27. • Hypothesis testing for Population proportion
number of successes x
– Sample proportion p =
ˆ =
sample size n
– Proportion always between 0 and 1
Testing H0: p = p0 for n ≥ 30
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
H1: p ≠ p0 |z| ≥ Z1- α/2 p  p0
ˆ
z
H1: p > p0 z ≥ Z1- α p0 (1  p0 )
H1: p < p0 z ≤ -Z1- α n 27

28. • Example
– A market research company investigates the claim of a
supplier that 35% of potential buyers are preferring their
brand of milk
– A survey was done in several supermarkets and it was
found that 61 of the 145 shoppers indicated that they will
buy the specific brand of milk
– Assist the research company with the claim of the supplier
on a 10% level of significance.
28

29. • Solution
– The population of interest is the proportion of buyers
– Want to test the claim that the proportion is 35% = 0,35
– H0 : p = 0,35
– The alternative hypothesis must specify that the proportion
is not 35%
– H1 : p ≠ 0,35
– Sample proportion p = number of successes = x  61  0, 42
ˆ
sample size n 145
– Need to test if 0,42 p  is significant different from 0,35(p)
ˆ
29

30. • Solution
/2  0,05
At – = 0 : p = 0,35 not say
α H 0,10 we can
that 35%p ≠the clients will
– H1 : of 0,35 -z-1,65 z1-/2
1-/2 +1,65
prefer the brand of milk
– α = 0,10
Reject H0 Accept H0 Reject H0
p  p0
ˆ 0, 42  0,35
z   1, 76
p0 (1  p0 ) 0,35(1  0,35)
n 145
Z1-α/2 = Z0.95 = +/- 1.65
– Reject H0
30

31. • Hypothesis testing for Population Variance
– Draw conclusions about variability in population
– Χ2 –distribution with (n - 1) degrees of freedom
Testing H0: σ2 = σ20
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
Χ2 ≤ Χ2n-1;α/2 or
H1: σ2 ≠ σ20 (n  1) s 2
Χ2 ≥ Χ2n-1;1- α/2 2 
H1: σ2 > σ20 Χ2 ≥ Χ2n-1;1- α  02
H1: σ2 < σ20 Χ2 ≤ Χ2n-1;α 31

32. Concept Questions
• Questions 20 – 24 page 272
32

33. • Example
– The variation in the content of a 340ml can of beer should
not be more than 10ml2.
– To test the validity of this, 25 cans of beers revealed a
variance of 12ml2.
– On a 5% level of significance can we say the variation in
the content of the cans is too large?
33

34. • Solution
– The population of interest is the variation in content
– Want to test the claim that the variance is more than 10ml2
– H1 : σ2 > 10
– The null hypothesis must specify that the variance is 10ml2
– H0 : σ2 = 10
– Need to test if 12(s2) is significant more than 10(σ2)
34

35. • Solution
– H0 : σ2 = 10   0,05
– H1 : σ2 > 10
– α = 0,05 Χ2n – 1; 1-α
+36,42
(n  1) s 2
(25  1)12
 
2
  28,8 Accept H0 Reject H0
 02 10
At α = 0,05 we can not say
– Accept H0 that the variation in the
content of the cans is more
Χ n-1; 1-α = Χ 24; 0.95 = 36.42
2 2
than 10ml2
35

36. • Hypothesis tests for comparing two
Populations Drawn from different
– Difference between two means
samples, samples
have no relation
• Independent samples
– Large samples
– Small samples Samples are
• Dependent samples related
– Difference between two proportions
– Difference between two variances 36

37. • Hypothesis tests for comparing two Populations
– H0: Population 1 parameter = Population 2 parameter
– H1: Population 1 parameter ≠ Population 2 parameter
– H1: Population 1 parameter > Population 2 parameter
– H1: Population 1 parameter < Population 2 parameter
μ1 / σ21 / p1 μ2 / σ22 / p2

38. Difference between two Population Means,
independent samples, n1 ≥ 30 and n2 ≥ 30
Testing H0: μ1 = μ2 for n1 ≥ 30 and n2 ≥ 30
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
H1: μ1 ≠ μ2 |z| ≥ Z1- α/2 x1  x2
z
H1: μ1 > μ2 z ≥ Z1- α s12 s2
2

H1: μ1 < μ2 z ≤ -Z1- α n1 n2
38
Use σ12 and σ22 if known

39. Example
A leading television manufacturer purchases
cathode ray tubes from 2 businesses (A and B). A
random sample of 36 cathode ray tubes from
business A showed a mean lifetime of 7.2 years
and a std dev of 0.8 years, while a random sample
of 40 cathode ray tubes from business B showed a
mean lifetime of 6.7 years and a std dev of 0.7 yrs.
Test at a 1% significance level whether the mean
lifetime of the cathode ray tubes from business A is
longer than the mean lifetime of business B
39

40. Answer
Company A: n1 = 36, x1 = 7,2 and s1 = 0,8.
Company B: n2 = 40, x 2 = 6,7 and s2 = 0,7.
H0: 1 = 2

H1: 1 > 2

 = 0,01
x1  x 2
z=
s12 s2
2

n1 n 2
7,2  6,7
=
0,8 0,7
2 2
 
36 40
0,5
=
0,1733
 = 2,8852
Z1 = Z0,99 = 2,33

Therefore, reject H0.
There is enough evidence to say that the mean lifetime of the tubes from Company A is longer
than that of Company B.
40

41. Difference between two Population Means, independent
samples, n1 < 30 and n2 < 30
Testing H0: μ1 = μ2 for n1 < 30 and n2 < 30
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
x1  x2
H1: μ1 ≠ μ2 |t| ≥ tn1 + n2 – 2 ; 1- α/2 t with
1 2
sp 
n1 n2
H1: μ1 > μ2 t ≥ tn1 + n2 – 2 ; 1- α
sp 
 n1  1 s12   n2  1 s22
H1: μ1 < μ2 t ≤ -tn1 + n2 – 2 ;1- α n1  n2  2
41

42. Difference between two Population Means, dependent
samples – pairs of observations
Observation
1 2 3 ---------- n
Sample 1 X11 X12 X13 - - - - - - - - - - X1n
Sample 2 X21 X22 X23 - - - - - - - - - - X2n
d1 d2 d3 dn
Difference (d)
(X11 - X21) (X12 - X22) (X13 – X23) (X1n - X2n)
d  d 
2
1
2
 1
d   d and sd  n
n n 1 42

43. Difference between two Population Means, dependent
samples
Testing H0: μ1 = μ2
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
H1: μ1 ≠ μ2 |t| ≥ tn – 1 ; 1- α/2 d
t
H1: μ1 > μ2 t ≥ tn – 1 ; 1- α  sd 
 
 n
H1: μ1 < μ2 t ≤ -tn – 1 ;1- α
43

44. Concept Questions
Questions 25 – 29 p 283, textbook
44

45. Difference between two Population Proportions, large
independent samples
Testing H0: p1 = p2 for n1 ≥ 30 and n2 ≥ 30
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
H1: p1 ≠ p2 |z| ≥ Z1- α/2 p1  p2
ˆ ˆ
z
1 1
p(1  p)   
ˆ ˆ
H1: p1 > p2 z ≥ Z1- α  n1 n2 
n1 p1  n2 p2
ˆ ˆ
H1: p1 < p2 z ≤ -Z1- α where p 
ˆ 45
n1  n2

46. Difference between two Population Variances, large
independent samples
Testing H0: σ21 = σ22
Alternative Decision rule:
Test statistic
hypothesis Reject H0 if
H1: σ21 ≠ σ22 F ≥ Fn1-1 ; n2-1 ; α/2 s12
F 2
H1: σ21 > σ22 F ≥ Fn1-1 ; n2-1 ; α s2
Assume population 1 has the larger
46
variance. Thus always: s21 > s22

47. • Example
• There is a belief that people staying in Cape Town
travel less than people staying in Johannesburg.
– Random samples of 43 people in Cape Town and 39
in Johannesburg were drawn.
– For each person the distance travelled during
October were recorded.
– Test the belief on a 5% level of significance
47

48. • Solution
– The population of interest is the km travelled
– Samples are large and independent
– We want to show that Cape Town travel less than
Johannesburg
– H1 : μ1 < μ2
– The null hypothesis must specify a single value of the
parameter 
– H0 : μ1 = μ2
48

49. The belief that people staying in
• From the data: Cape Town travel less than people
–
Cape Town Johanesburg in Johannesburg is not true
staying
x1 = 604 x 2 = 633a 5% level of significance
on
n1 = 43 n 2 = 39
s1 = 64 s 2 = 103 -1,65 0
Reject H0 Accept H0
– H0: μ1 = μ2
– H1: μ1 < μ2
– z  x1  x2  604  633  1,51
2 2 2 2
s1 s2 64 103
 
n1 n2 43 39
– Accept H0 49

50. Example
• Pathological laboratories have a problem with time it takes a
blood sample to be analyzed. They hope by introducing some
new equipment, the time taken will be reduced.
– Blood samples for 10 different types of test were analyzed by
the traditional laboratories and by the newly equipped
laboratories.
– The time, in minutes, were captured for each test.
– Did the time reduce? α = 0,01
50

51. • Solution
– The population of interest is the test times
– The samples are dependent
– We want to show that new times is less than the old times
– H1 : μ1 > μ2
– The null hypothesis must specify a single value of the
parameter
– H0 : μ1 = μ2
51

52. Blood Existing New
Difference - Calculate the
sample lab lab
1 47 70 -23 difference for each xi
2 65 83 -18 - Calculate the average
3 59 78 -19 differences and the
4 61 46 15 standard deviation of
5 75 74 1 the differences
6 65 56 9
7 73 74 -1
x d  2, 2
8 85 52 33
9 97 99 -2 sd  19,14
10 84 57 27
52

53. - The hypotheses test for this
problem is
H0: 1 = 2
H1: 1 > 2 α =0,10
- The statistic is 0 1,383
t0.90,9
d
t Accept H0 Reject H0
 sd 
 
 n
2, 2 Using α = 0,10, introducing
 some new equipment the
19,14 10 time taken did not reduce.
53
 0, 36

54. • Example
– A clothing manufacturer introduced two new swim suit ranges
on the market.
– Of the 266 clients asked if they will wear range A, 85 indicated
they will.
– Of the 192 clients asked if they will wear range B, 50 indicated
they will.
– Can we say there is a difference in the preferences of the two
ranges. Use α = 0,05.
54

55. • Solution
– The population of interest is the proportion of clients who
will wear the clothing
– We want to determine if the proportion of range A differ form
the proportion of range B
– H1: p1 ≠ p2
– The null hypothesis must specify a single value of the
parameter
– H0: p1 = p2
55

56. • From the data:
– Range A : p1  266  0,32
ˆ 85
Range B: p2  192  0, 26
ˆ 50
266(0,32)  192(0, 26)
– p
ˆ  0, 29
266  192 +1,96
-1,96
– H0: p1 = p2 Reject H0 Accept H0 Reject H0
– H1: p1 ≠ p2
– p1  p2
ˆ ˆ 0,32  0, 26
z   1,93
1 1
p(1  p)   
ˆ ˆ 
0, 29(1  0, 29) 266  192
1 1

 n1 n2 
– Accept H0 There is no difference in the preferences
of the two ranges if α = 0,05. 56

57. • Example Remember:
– An important measure to determine 1 has the largerin the
Population service delivery variance.
banking sector is the variability in the service 2times.
Thus always: s21 > s 2
– An experiment was conducted to compare the service times of
two bank tellers.
– The results from the experiment:
• Teller A: nA = 18 and s2A = 4,03
• Teller B: nB = 26 and s2B = 9,49
– Can we say that the variance in service time of teller A is less
than that variance of teller B on a 5% level of significance.
– We will then test if the variance in service time of teller B is
more that the variation of teller A: s2B > s2A 57

58. • Solution
– The population of interest is the variation in the service time
of the two bank tellers.
– We want to determine if the variation of teller B is more than
the variation of teller A.
– H1: S21 > S22
– The null hypothesis must specify a single value of the
parameter
– H0: S21 = S22
58

59. • From the data:
– The results from the experiment:
• Teller A: nA = 18 and s2A = 4,03
• Teller B: nB = 26 and s2B = 9,49 F26-1;18-1;0,05 = 2,18
Accept H0 Reject H0
– H0: 1 = S22
S2
– H1: S21 > S22
S 2
9, 49 Variation of teller B is more
F 1
2
 2,35 than the variation of teller A
S 4, 03
2
on a 5% level of
– Reject H0 significance.
59

60. Concept Questions
• Questions 30 -31, p 289, textbook
60

61. HOMEWORK
• Self review test, p289
• Izmivo
• Revision test
• Supplementary Questions p292 – 298
61