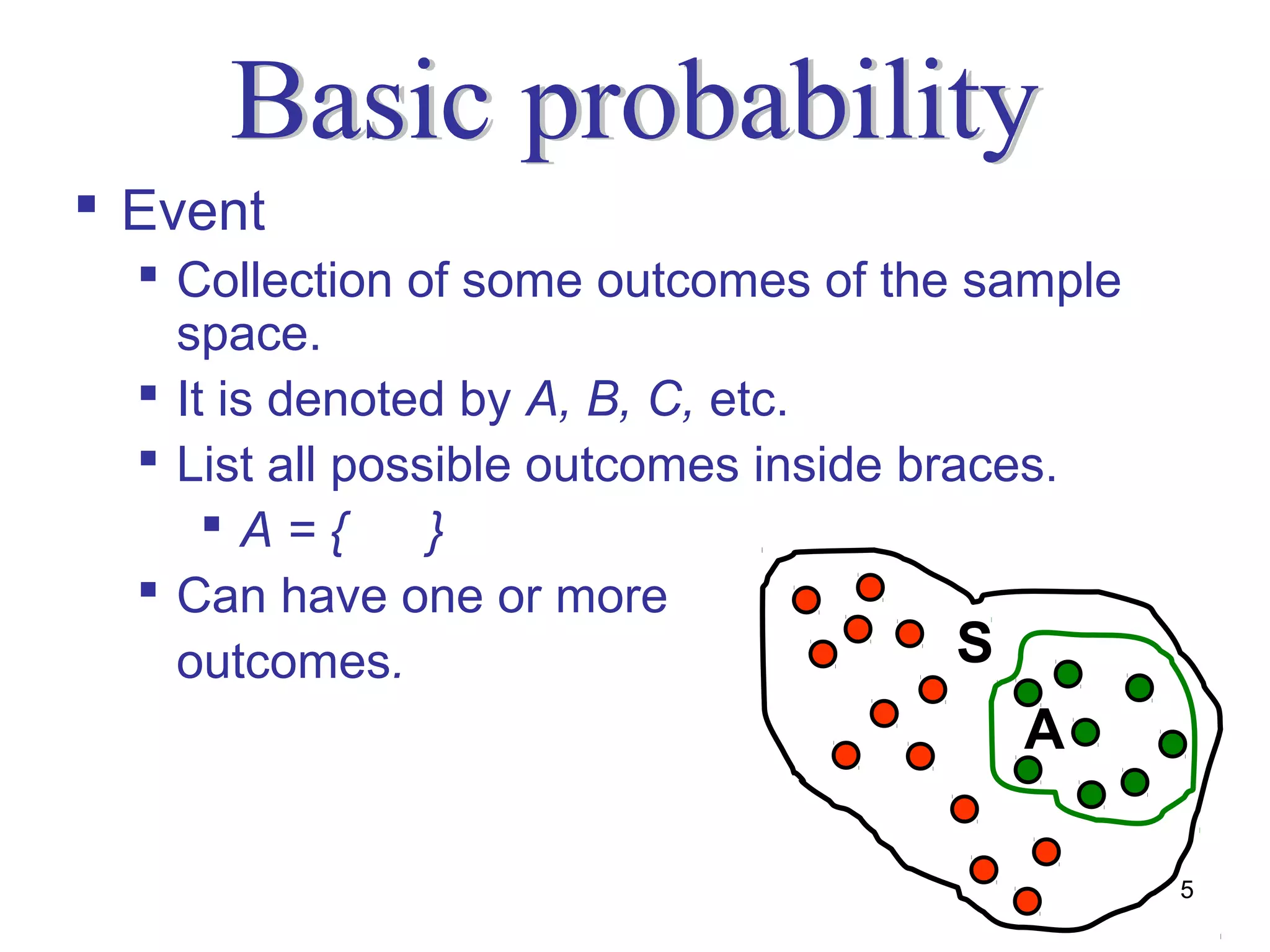
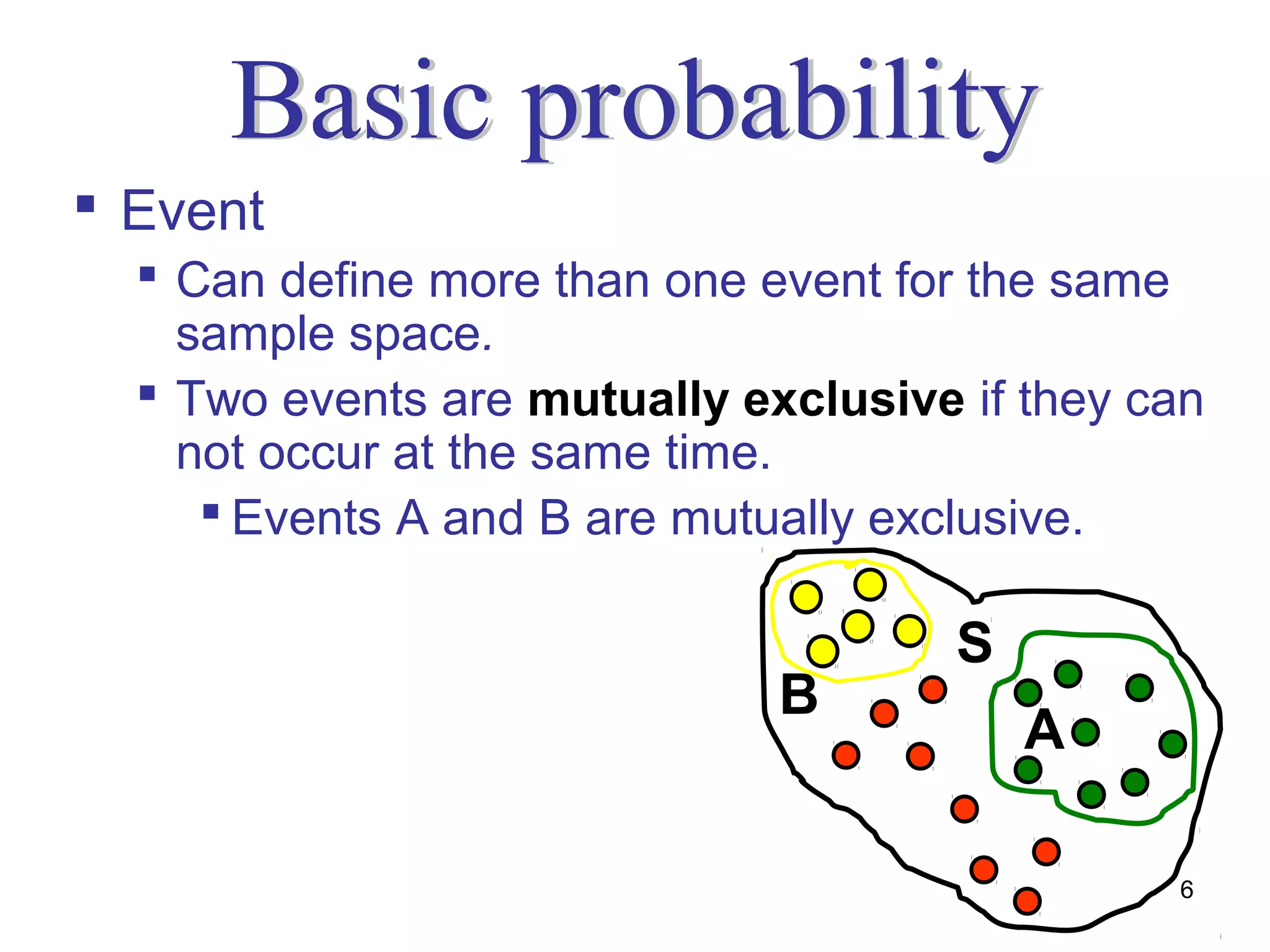
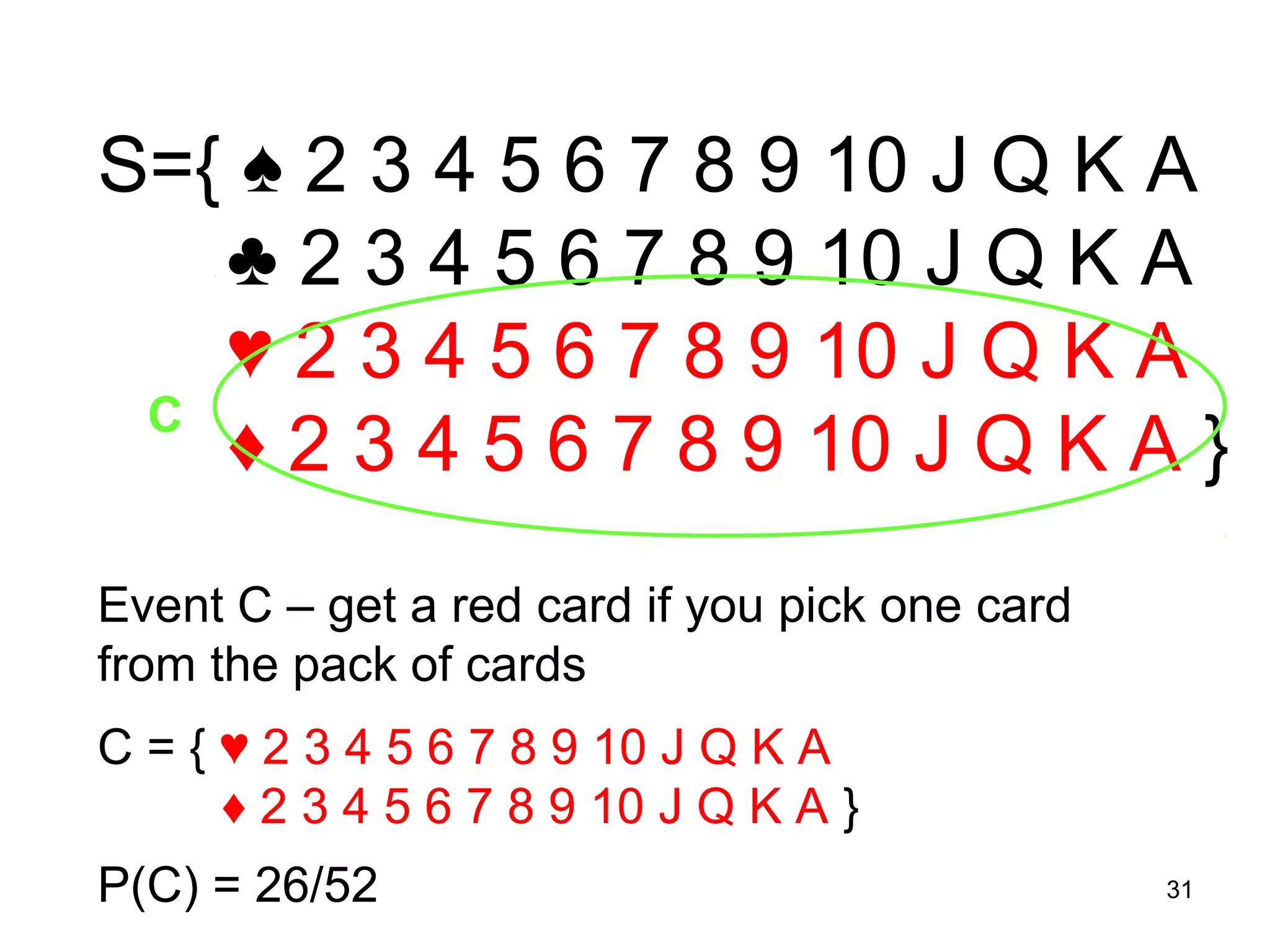
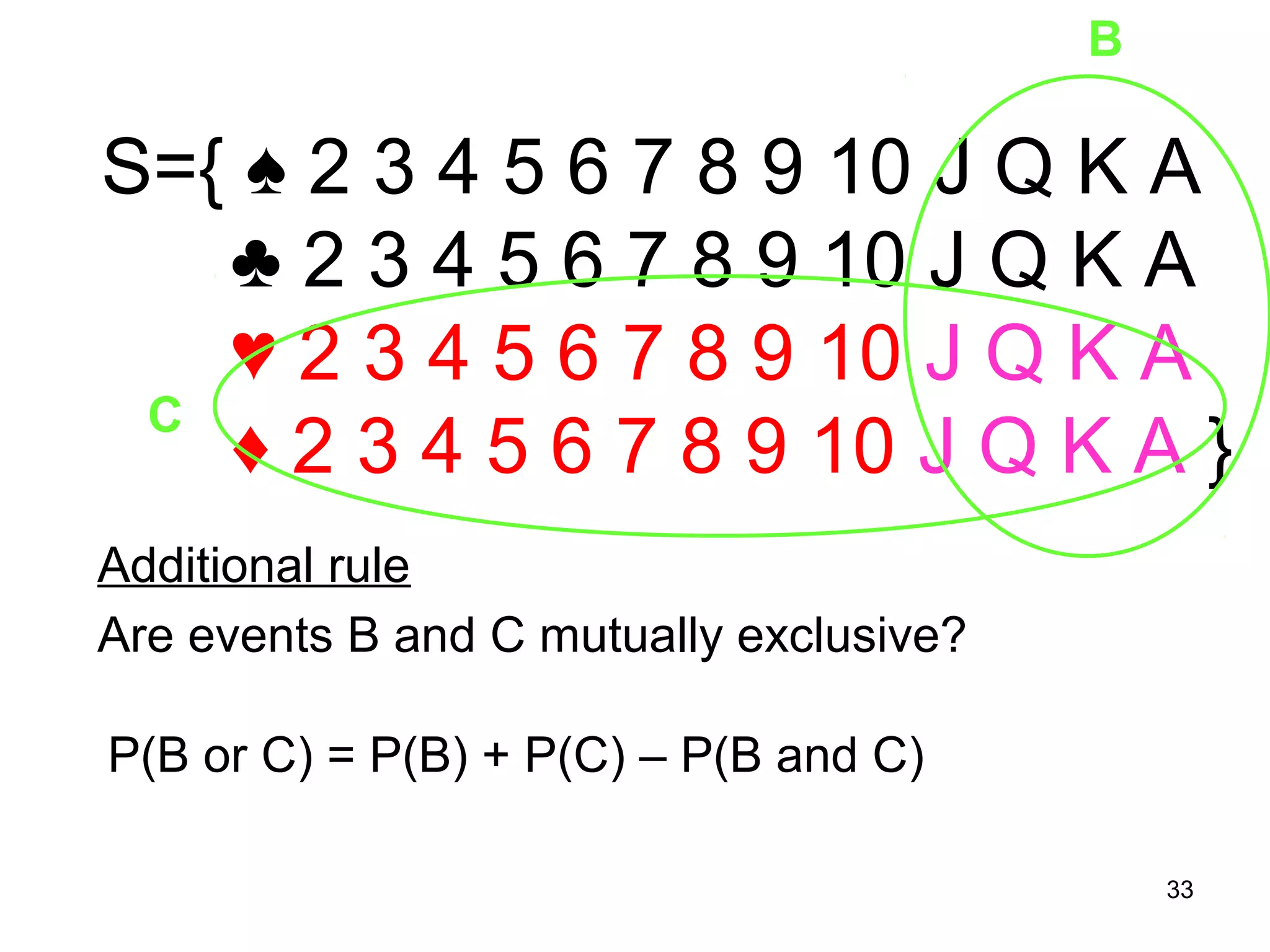
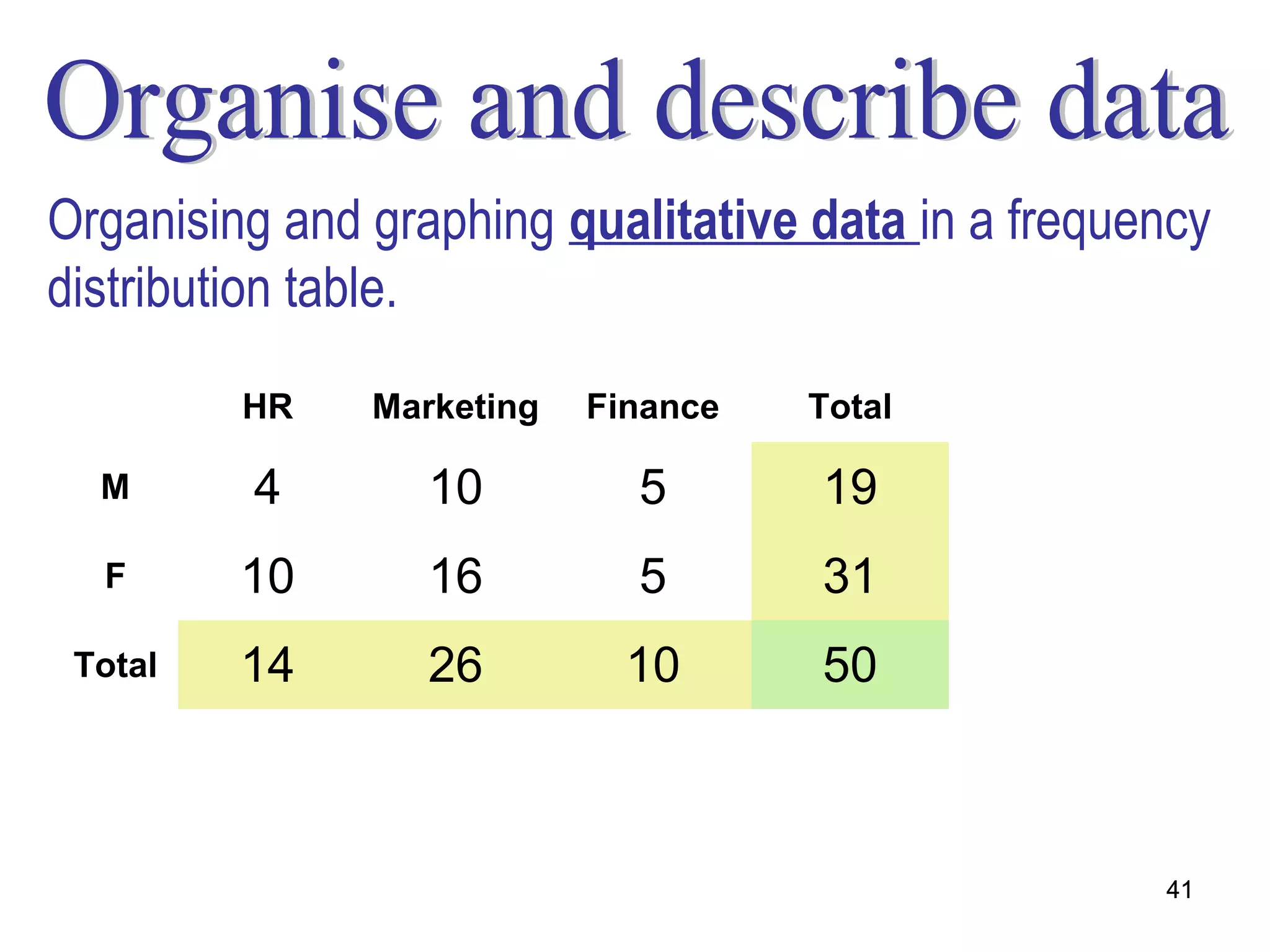
The document defines probability as a numerical value between 0 and 1 used to express the likelihood of an event occurring. It explains the different approaches to probability including relative frequency, classic, and subjective. Examples are provided to illustrate concepts such as sample space, events, mutually exclusive and non-mutually exclusive events, conditional probability, independent events, and counting rules for probability calculations.

2.  What is probability?
 Probability is a numerical value used to
express the chance that a specific event
will occur.
 Probability is always in the interval 0 to 1
and can be expressed as percentages.
 The greater the chance that an event will
occur, the closer the probability is to 1.
 The smaller the chance that an event will
occur, the closer the probability is to 0.
 Probabilities is needed to make
generalisations about the population based
2
on a sample drawn from the population.

3.  Experiment
 Process that results in obtaining observations
from an experimental unit.
 Experimental unit is the object on which the
observations are made.
 Results of experiment are called outcomes.
 Stochastic experiment
 The results are a definite set of two or more
possible outcomes.
 The outcome can not be determined in advance.
 Can be repeated under stable conditions.
3

4.  Sample space
 Collection of all possible outcomes of an
experiment.
 It is denoted by S.
 List all possible outcomes inside braces.
S={ }
S
4

5.  Event
 Collection of some outcomes of the sample
space.
 It is denoted by A, B, C, etc.
 List all possible outcomes inside braces.
A={ }
 Can have one or more
outcomes. S
A
5

6.  Event
 Can define more than one event for the same
sample space.
 Two events are mutually exclusive if they can
not occur at the same time.
 Events A and B are mutually exclusive.
S
B
A
6

7.  Event
 Can define more than one event for the same
sample space.
 Two events are non mutually exclusive if they
can occur at the same time.
 Events A and C are non mutually exclusive.
 Probability of an event
 Probability of Event A.
S
 P(A) A
C 7

8.  Properties of probability:
 0 ≤ P(A) ≤ 1
 P(B) = 0
 B impossible event
 P(C) = 1
 C certain event
 P(S) = 1
 Compliment of Event A:
 P(Ā) = 1 – P(A)
 Events A and B mutually exclusive.
 P(A or B) = P(A) + P(B)
8

9. Three approaches to probability
 1. Relative frequency approach
 The probabilities of the outcomes differ.
 Counting the number of times that an event
occurs when performing an experiment a
large number of times.
number of times event A occurred
P(event A) =
number of times the experiment was repeated
f
P ( A) =
n
9

10. Three approaches to probability
 Relative frequency approach
 Example
 In a group of 20 tourists staying in a hotel,
nine prefer to pay cash for their
accommodation.
 The probability that a tourist will pay cash
for accommodation is:
f 9
P ( A) = = = 0, 45
n 20
10

11. Three approaches to probability
 2. Classic approach
The outcomes all have the same probabilities.
Not necessary to performing an experiment a
number of outcomes of experiment favourable to the event
P(eventA) =
total number of outcomes of experiment
f
P ( A) =
n
11

12. Three approaches to probability
 Classic approach
 Example
 Chance to get an uneven number on a dice:
 S = {1; 2; 3; 4; 5; 6}
 F = {1; 3; 5}
1 1 1 3
P( F ) = + + = = 0,5
6 6 6 6
12

13. Three approaches to probability
 3. Subjective approach
 The probabilities assigned to the outcomes of
the experiment is subjective to the person who
performs the experiment.
13

14.  The word “or” in probability is an indication of
addition
 P(A or B)
 The word “and” in probability is an indication of
multiplication
 P(A and B)
14

15. Addition rules for calculating probabilities
 Events are mutually exclusive when they
have no outcomes in common.
 For mutually exclusive events:
 P(A or B)
= P(A) + P(B)
= 4/21 + 3/21
= 7/21
B
Events A and B A
are mutually S
exclusive 15

16. Addition rules for calculating probabilities
 Events are mutually exclusive when they
have no outcomes in common
 If events are not mutually exclusive
 P(C or D) = P(C) + P(D) – P(C and D)
 P(C and = 5/21 + 5/21 – 2/21 = 8/21
D)
 Outcomes are included in C and D.
Events C and D are
not mutually
exclusive S
16

17. Conditional probability
 Need to know the probability of an event
given another event has already occurred
 The two events must be dependent.
 Probability of A, given B has occurred:
P ( A and B )
 P(A|B) = , P(B) ≠ 0
P( B)
 Multiplication rule: The outcome of one event
affects the probability of the
 P(A and B) = P (B)P(A|B)
 Probability of B, given A has occurred: event.
occurrence of another
P ( A and B )
 P(B|A) = , P(A) ≠ 0 17
P( A)

18. Conditional probability
 Need to know the probability of an event
given another event has already occurred.
 If sampling without replacement takes place.
 The events are considered dependent.
 Example – Three students need to pick a
biscuit from a plate with 10 biscuits.
 1st student can pick any of the 10 biscuits.
 2nd student has only 9 biscuits to pick from.
 3rd student has only 8 biscuits to pick from.
 The probability to pick the 1st biscuit is 1/10, the 2nd
is 1/9 and the 3rd is 1/8. 18

19. Independent Events
 Events are statistically independent if the
outcome of one event does not affect the
probability of occurrence of another event.
P(A|B) = P(A)
P(B|A) = P(B)
Multiplication rule for dependent events:
 P(A and B) = P(B)P(A|B)
Multiplication rule for independent events:
 P(A and B) = P(A)P(B)
19

20. Counting rules
 Multi-step experiments
 The number of outcomes for ‘k’ trails each with the
same ‘n’ possible outcomes.
 The number of outcomes in S = nk.
 Example
 How many ways can 10 multiple choice question
with 4 possible answers be answered:
 410 = 1 048 576 ways
20

21. Counting rules
 Multi-step experiments
 The number of outcomes for ‘j’ trails each with a
different number of ‘n’ outcomes.
 The number of outcomes in S = n1 x n2 … X nj
 Example
 Need to order a meal where you can pick ‘1’
burger from ‘8’, ’1’ cool drink from ’10’, ‘1’ ice
cream from ‘5’.
 Number of possible orders: 8×10×5 = 400
21

22. Counting rules
 The factorial
 The number of ways in which ‘r’ objects can be
arranged in a row, without replacement.
 r! = r×(r – 1)×(r – 2)× …×3×2×1
 Note r! = 0! = 1
 Example
 Six athletes compete in a race. The number of
order arrangements for completing the race.
 6! = 720 different ways
22

23. Counting rules
 Combination
 Select r objects without replacement from a larger
set of n objects, order of selection not important.
 n!
n Cr =
r !(n − r )!
 Example
 Six lotto numbers should be selected form a
possible 49 – order of selection not important.
 C = C = 49!
n r 49 6 = 13 983 816
6!(49 − 6)!
23

24. Counting rules
 Permutation
 Select r objects without replacement from a larger
set of n objects, order of selection is important.
 n!
nP =
r
(n − r )!
 Example
 Six athletes in a race, how many ways to
compete for the gold, silver and bronze medals.
 6!
n Pr = 6 P3 = = 120
(6 − 3)!
24

25. Additional examples
25

26. Experiment: Draw a card from a play pack of cards
Experimental unit: Play pack of cards
Outcome of experiment: Any card from the pack
Sample space:
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
52 Cards in the pack 26

27. A
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Event - some outcomes of the sample space
Event A – get a ‘4’ if you pick one card from the
pack of cards
A = {♠4 ♣4 ♥4 ♦4}
P(A) = 4/52 27

28. B
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Event - some outcomes of the sample space
Event B – get a picture card if you pick one card
from the pack of cards
B = {♠JQKA ♣ JQKA ♥ JQKA ♦ JQKA}
P(B) = 16/52 28

29. B
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Complement of an event
Event B – get a picture card if you pick one card
from the pack of cards
What is the probability not to get a picture card?
P( B) = 1 – P(B) = 1 – 16/52 = 36/52 29

30. B
A
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Additional rule
Are events A and B mutually exclusive?
P(A or B) = P(A) + P(B) = 4/52 + 16/52 = 20/52
30

31. S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
C
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Event C – get a red card if you pick one card
from the pack of cards
C = { ♥ 2 3 4 5 6 7 8 9 10 J Q K A
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
P(C) = 26/52 31

32. B
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
C
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Additional rule
Are events B and C mutually exclusive?
32

33. B
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
C
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Additional rule
Are events B and C mutually exclusive?
P(B or C) = P(B) + P(C) – P(B and C)
= 16/52 + 26/52 – 8/52 = 34/52
33

34. B
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
C
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Conditional rule
What is the probability to get a red card if the
card must be a picture card?
8
P (C and B ) 52 = 8
P(C | B ) = =
P( B) 16 16 34
52

35. A
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
C
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Conditional rule
What is the probability to get a ‘4’ if the card
must be a red card?
2
P( A and C ) 52 = 2
P( A | C ) = =
P(C ) 26 26
52 35

36. A
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
C ♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Conditional rule
Sampling with replacement takes place
If we pick two cards, what is the probability that the
first one is red and the second one is ‘4’
We know: P(C) = 26/52 and P(A|C) = 2/26
2
P( A and C ) = P (C ) × P ( A | C ) = 26 ×2 = 36
52 26 52

37. A B
S={ ♠ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♥ 2 3 4 5 6 7 8 9 10 J Q K A
♦ 2 3 4 5 6 7 8 9 10 J Q K A }
Conditional rule
Sampling without replacement takes place
If we pick two cards, what is the probability that the
first one is a picture card and the second one is ‘4’
P(B) = 16/52 and P(A|B) = 4/51
64
P( B and A) = P ( B ) × P ( A | B ) = 16 ×4 = 37
52 51 2652

38. Independent events
A soccer team is playing two matches on a specific
day.
•The chance of winning the first match is:
•P(1st) = ½
•The chance of winning the second match is:
•P(2nd) = ½
•Will the outcome of the first match influence the
outcome of the second match?
•The chance of winning both matches is:
•P(1st and 2nd) = P(1st) x P(2nd |1st)
•P(1st and 2nd) = P(1st) x P(2nd) = ½ X ½ = ¼ 38

39. In chapter 2 we looked at an example to organise
qualitative data into a frequency distribution table.
39

40. Organising and graphing qualitative data in a
frequency distribution table.
Example:
The data below shows the gender of 50 employees and the
department in which they work at ABC Ltd.
HR – Human resources
Emp. no. Gender Dept. Emp. no. Gender Mark. – Marketing
Dept …..
1 M HR 6 M Fin. – Finance
Fin. …..
M – Male2 F Mark. 7 M Mark. …..
F – Female
3 M Fin. 8 M Fin. …..
4 F HR 9 F HR …..
5 F Fin. 10 F Fin. ….. 40

41. Organising and graphing qualitative data in a frequency
distribution table.
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
41

42. If one employee is chosen from the 50 employees, what is
the probability that the employee will be male?
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
P(M) = 19/50
42

43. If one employee is chosen from the 50 employees, what is
the probability that the employee will be from the
Marketing department?
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
P(Mark) = 26/50
43

44. If one employee is chosen from the 50 employees, what is
the probability that the employee will be from the
Marketing or Finance departments?
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
Are the marketing
P(Mark or Fin) = 26/50 + 10/50 = 36/50
and finance
departments 44
mutually exclusive?

45. If one employee is chosen from the 50 employees, what is
the probability that the employee will be Female and
from the Finance department?
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
Are female and the
P(F and Fin) = 5/50
finance department
mutually exclusive?
45

46. If one employee is chosen from the 50 employees, what is
the probability that the employee will be Female or from
the Finance department?
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
Are female and the
P(F or Fin) = 31/50 + 10/50 – 5/50 = 36/50
finance department
mutually exclusive?
46

47. If one employee is chosen from the 50 employees, what is
the probability that the employee will be from the
Marketing and Finance departments?
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
Are the marketing
P(F and Fin) = 0
and finance
departments 47
mutually exclusive?

48. If one employee is chosen from the 50 employees, what is
the probability that the employee will not be from the HR
department?
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
P(HR ) = 1 - P(HR) = 1 - 14/50 = 36/50
48

49. If one employee is chosen from the 50 employees, what is
the probability that the employee will female if she is
from the HR department?
HR Marketing Finance Total
M 4 10 5 19
F 10 16 5 31
Total 14 26 10 50
P(F|HR) = P(F and HR)/P(HR)
= 10/50 / 14/50 = 10/14 49