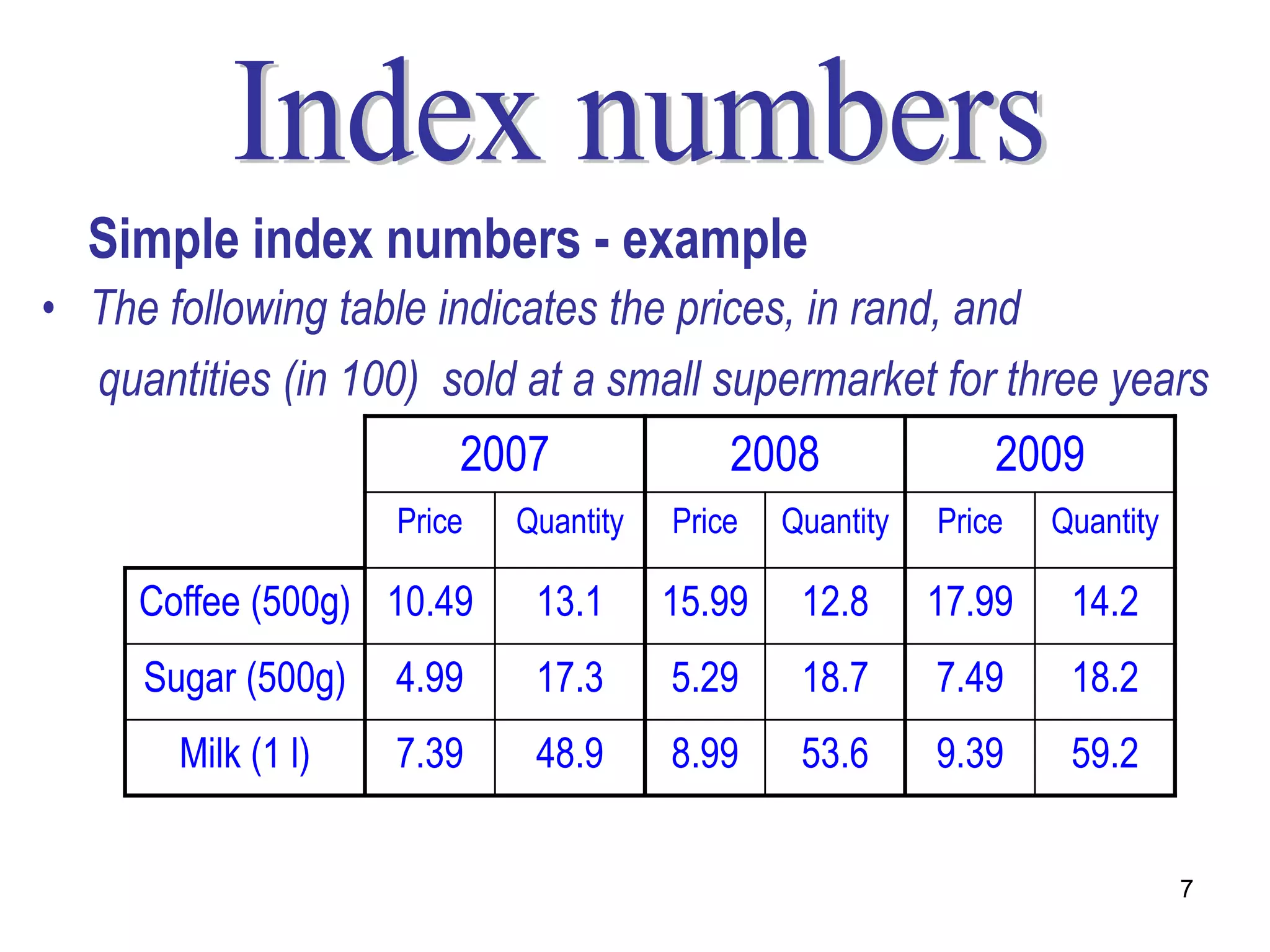
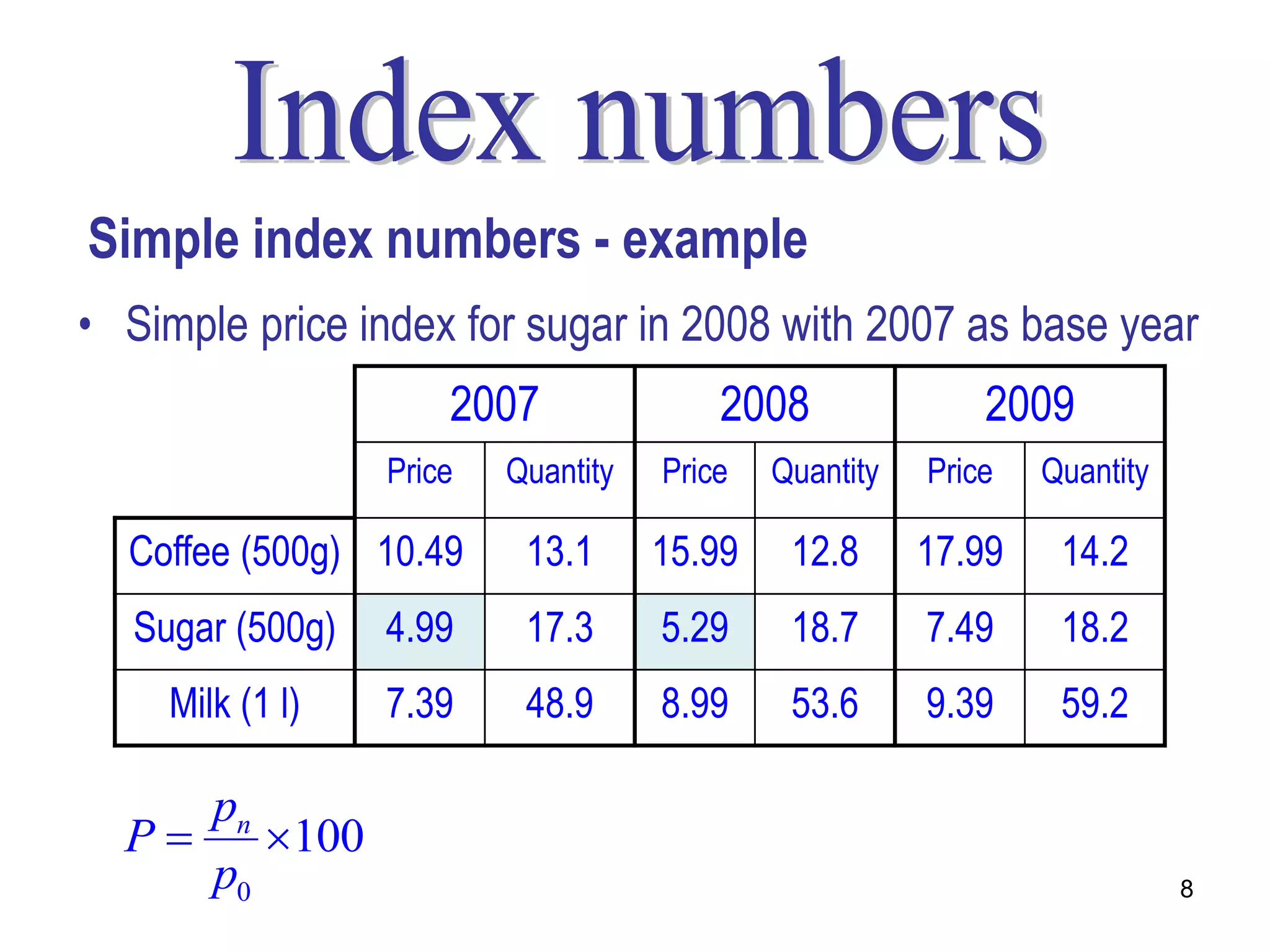
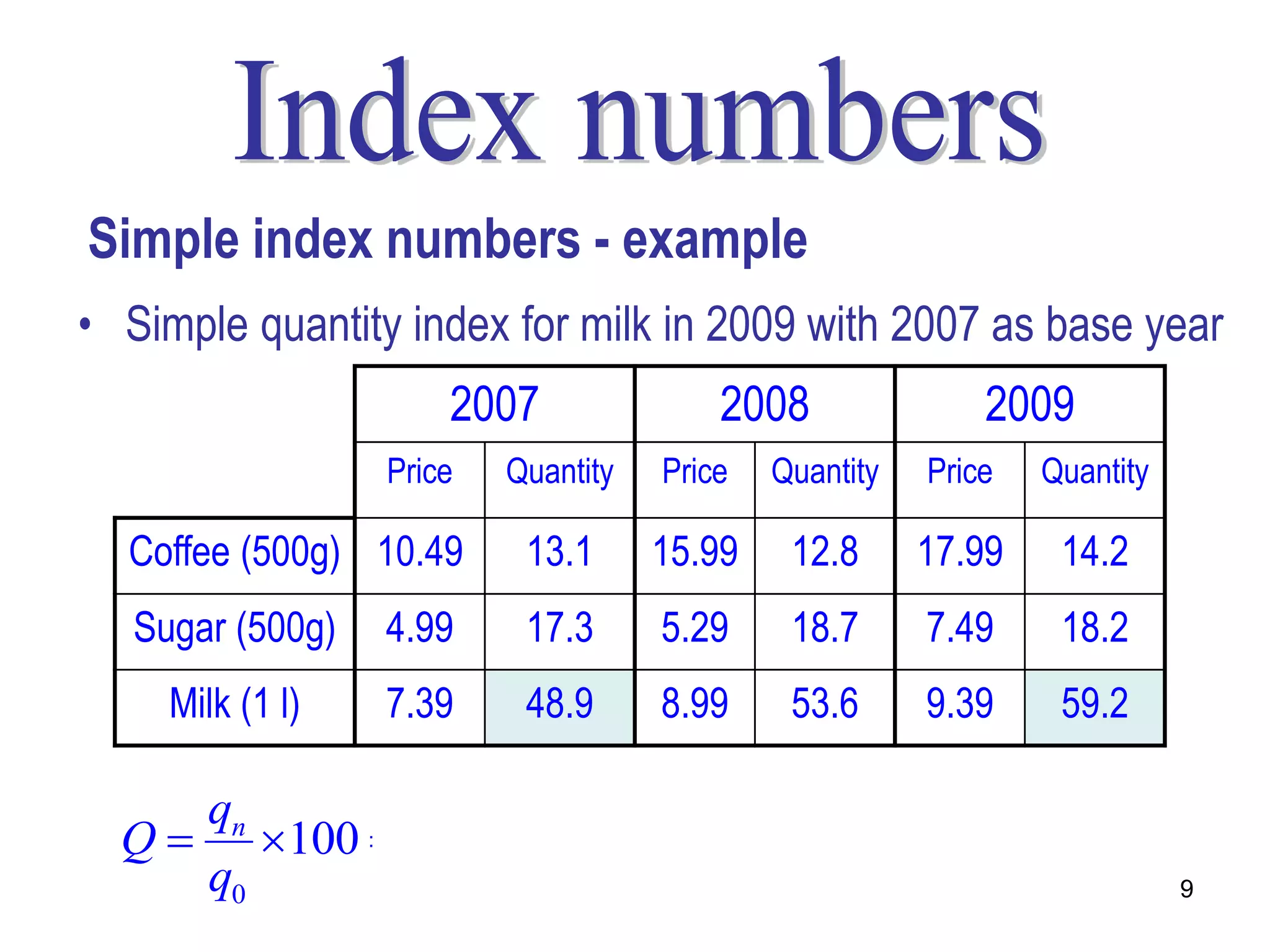
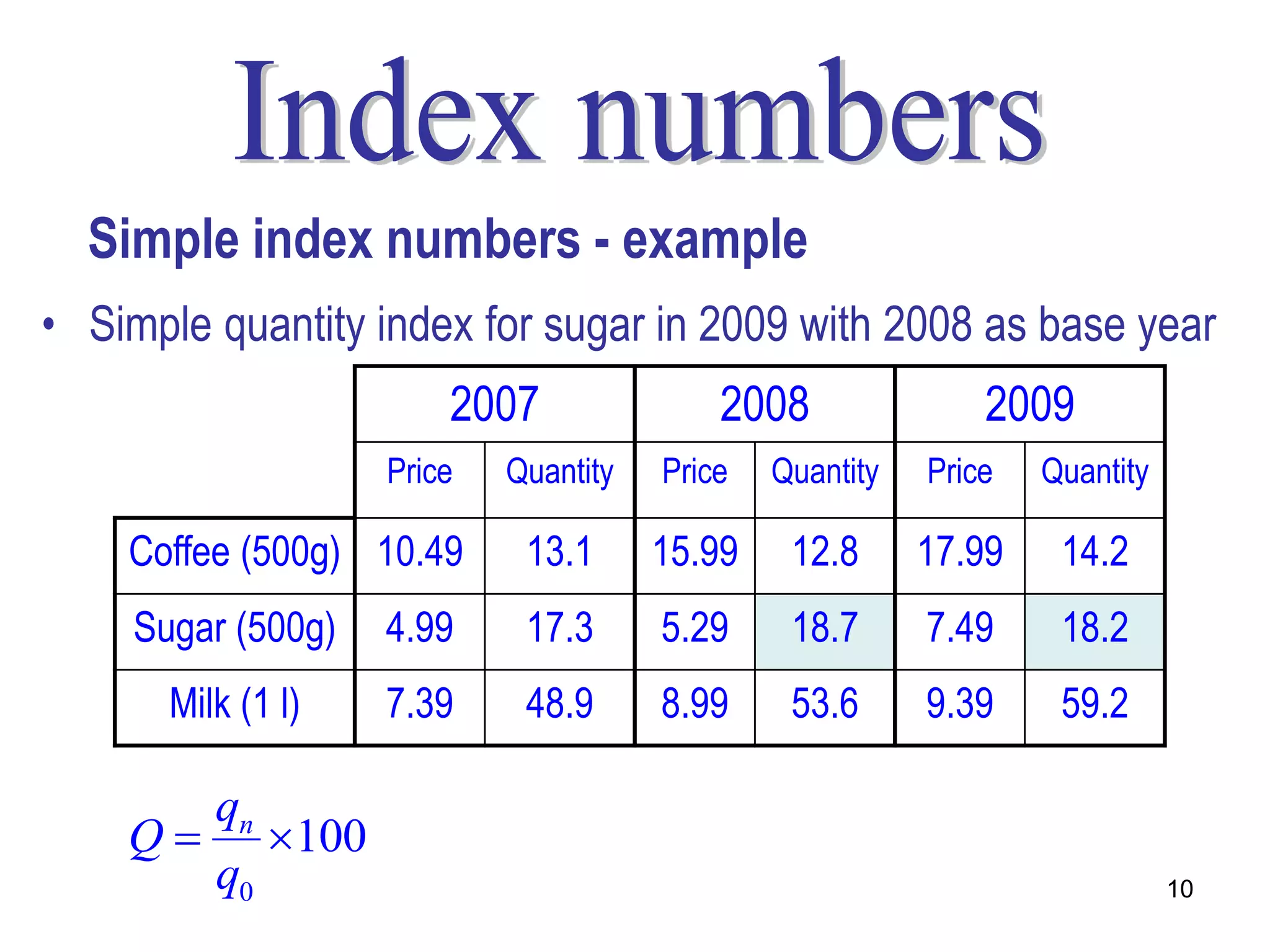
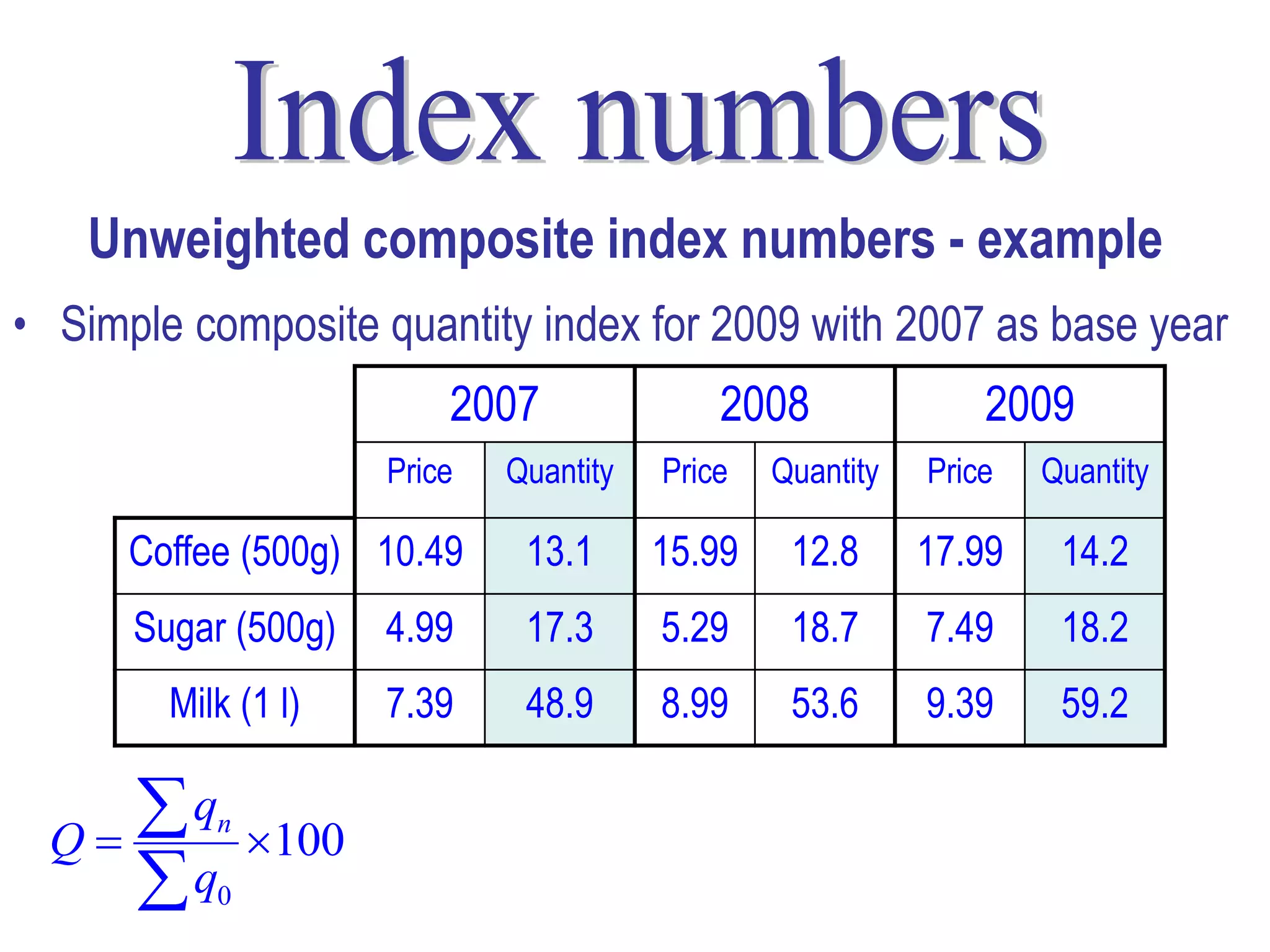
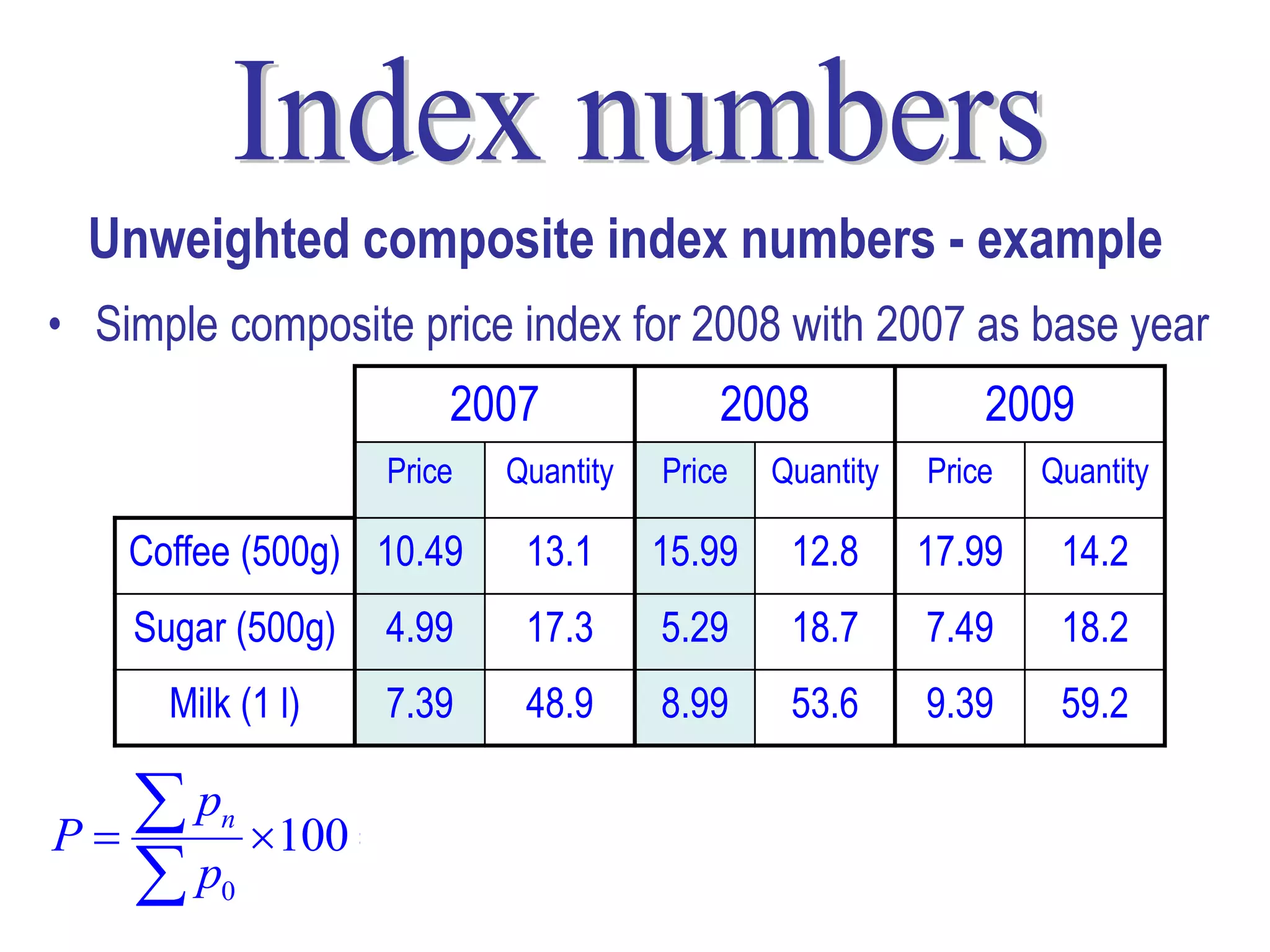
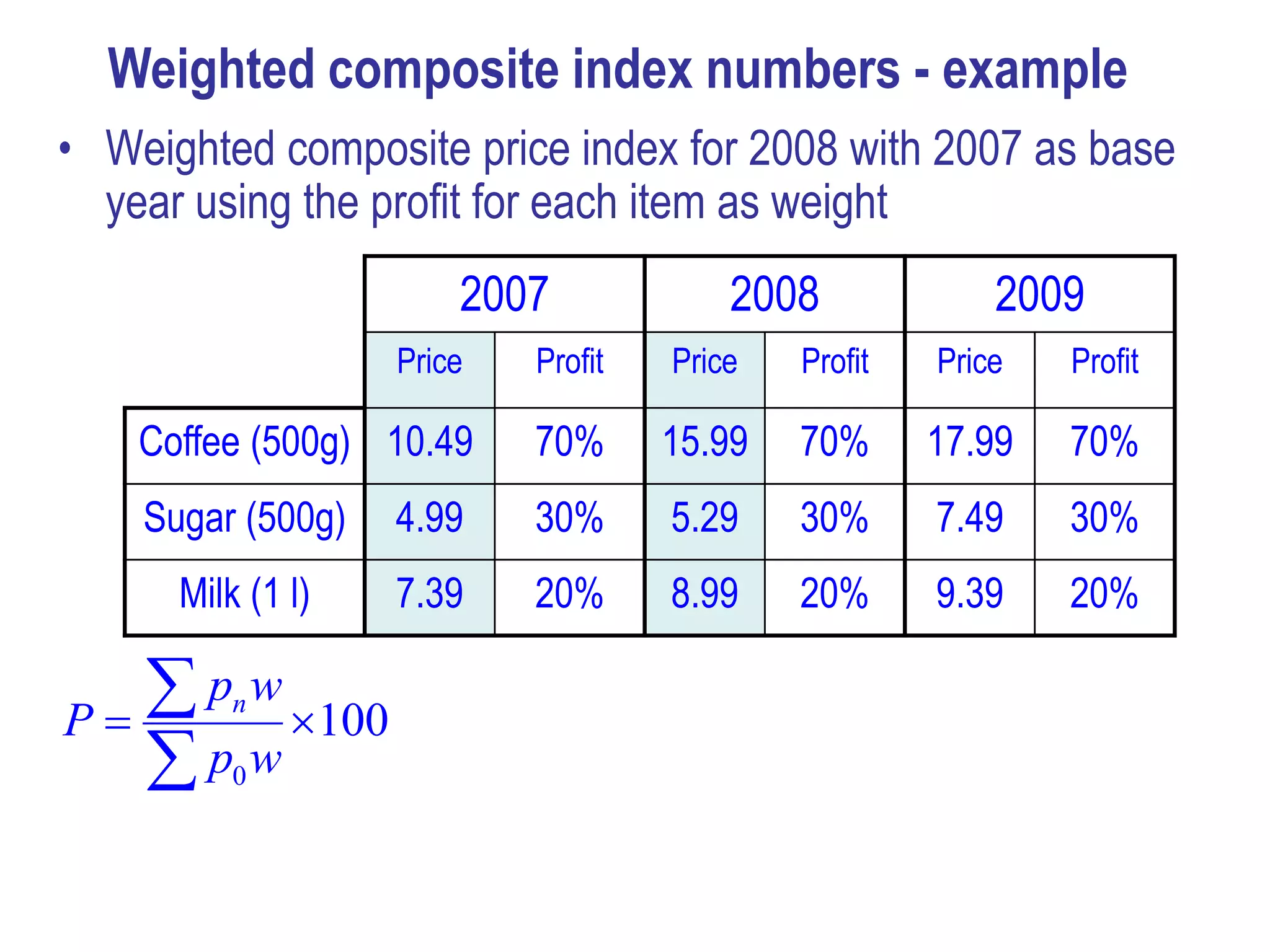
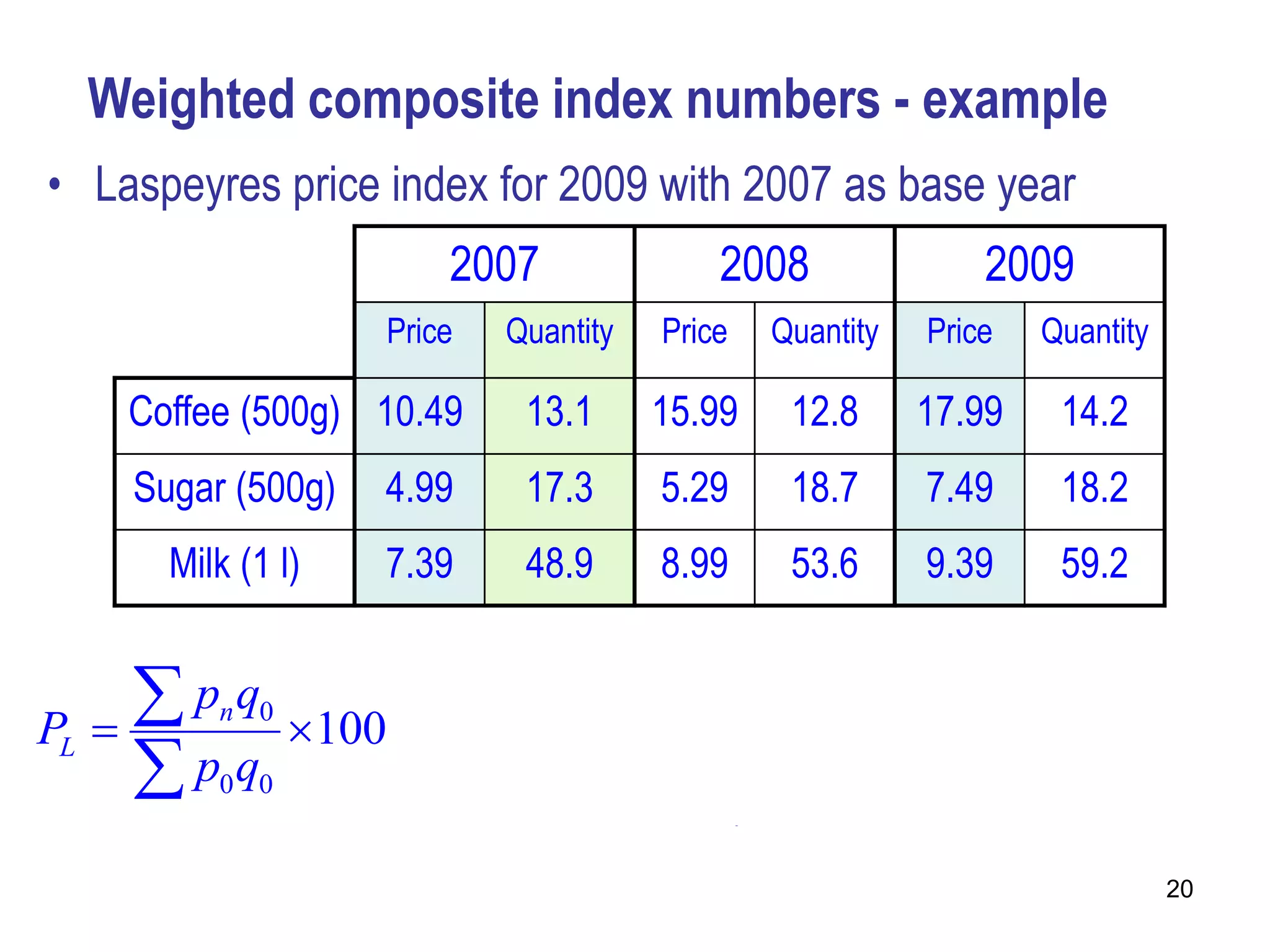
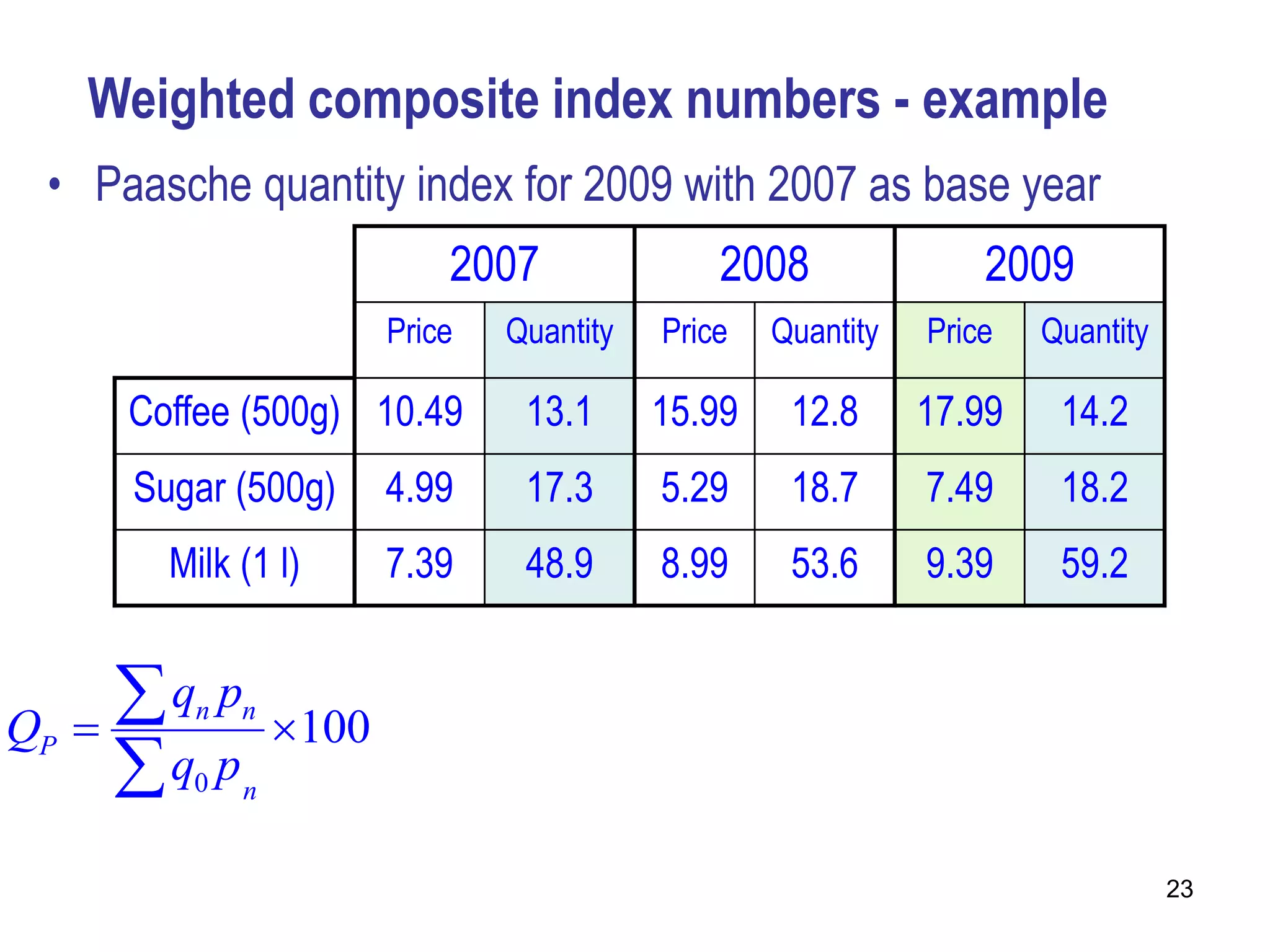
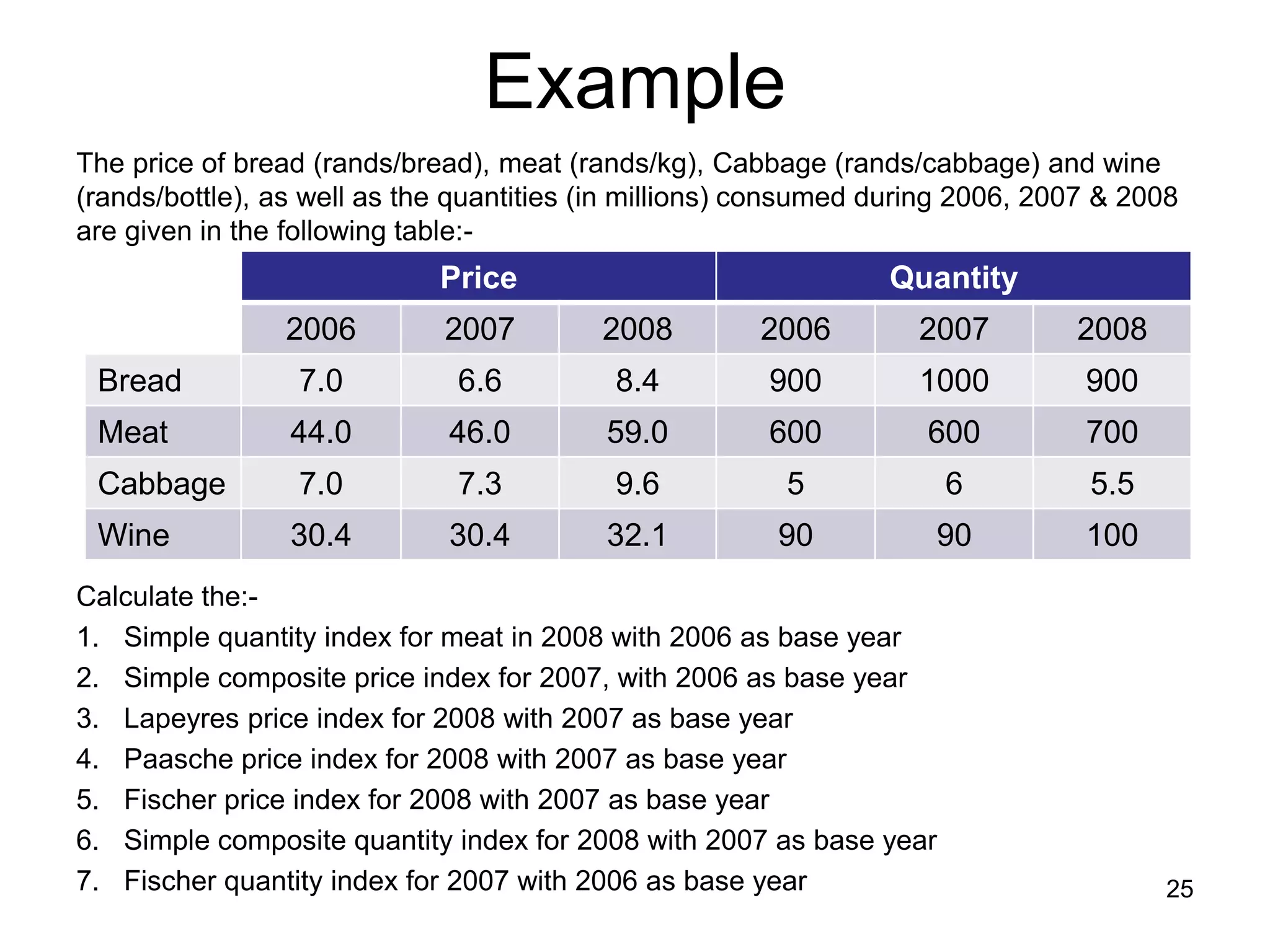
Here are the calculations for the indexes requested: 1. Simple quantity index for meat in 2008 with 2006 as base year Qn = 700 Q0 = 600 Index = Qn/Q0 * 100 = 700/600 * 100 = 116.67 2. Simple composite price index for 2007 with 2006 as base year ΣPn/ΣP0 * 100 = (6.6 + 46 + 7.3 + 30.4)/(7 + 44 + 7 + 30.4) * 100 = 103.57 3. Laspeyres price index for 2008 with 2007 as base year ΣPnQ0/ΣP0Q0 * 100 = (8.4

1. 1

2. • On the economic and business front many concepts
can be measured directly
• When it is not possible, need to introduce an
associated quantity to represent it
• Referred to as an index number
• Examples of index numbers
– Production Price Index
– Consumer Price Index
– JSE Mining, Industrial, Gold, All Share, Bond indices
– Business Confidence Index 2

3. What is an index number?
• A measure that summarises the change in the level of
activity, price or quantity, of a single item or a basket of
related items from one time period to another
• Expressing the value of an item in the period for which the
index is calculated as a ratio of its value in the base period
• Index is a percentage value
Period of reference
relative to which an
index is calculated 3

4. What is an index number?
• Index number = Value in period of interest × 100
Value in base period
• When the value exceeds 100, indicates an increase in the
level of activity
• When the value is less than 100, indicates a decrease in
the level of activity
Say: Index = 108.4
• Activity can indicate a change in price or quantity
Say: Index = 98.6
There was a:
– Price index There was a:
108.4 – 100 = 8.4%
– Quantity index 100 – 98.6 = 1.4%
increase
decrease 4

5. What is an index number?
• Price indices - P
– Price of the item in the period of interest – pn
– Price of the item in the base period – p0
• Quantity indices - Q
– Quantity of the item in the period of interest – qn
– Quantity of the item in the base period – q0
5

6. Simple index numbers
• Simple price index indicates the change in price of a
single item from the base period to the period under
consideration
pn
P 100
p0
• Simple quantity index indicates the change in quantity of a
single item from the base period to the period under
consideration
qn
Q  100
q0 6

7. Simple index numbers - example
• The following table indicates the prices, in rand, and
quantities (in 100) sold at a small supermarket for three years
2007 2008 2009
Price Quantity Price Quantity Price Quantity
Coffee (500g) 10.49 13.1 15.99 12.8 17.99 14.2
Sugar (500g) 4.99 17.3 5.29 18.7 7.49 18.2
Milk (1 l) 7.39 48.9 8.99 53.6 9.39 59.2
7

8. Simple index numbers - example
• Simple price index for sugar in 2008 with 2007 as base year
2007 2008 2009
Price Quantity Price Quantity Price Quantity
Coffee (500g) 10.49 13.1 15.99 12.8 17.99 14.2
Sugar (500g) 4.99 17.3 5.29 18.7 7.49 18.2
Milk (1 l) 7.39 48.9 8.99 53.6 9.39 59.2
pn 5.29
P 100  100  106.01 6.01 % increase
p0 4.99 8

9. Simple index numbers - example
• Simple quantity index for milk in 2009 with 2007 as base year
2007 2008 2009
Price Quantity Price Quantity Price Quantity
Coffee (500g) 10.49 13.1 15.99 12.8 17.99 14.2
Sugar (500g) 4.99 17.3 5.29 18.7 7.49 18.2
Milk (1 l) 7.39 48.9 8.99 53.6 9.39 59.2
qn 59.2
Q  100  100  121.06  21.06 % increase
q0 48.9 9

10. Simple index numbers - example
• Simple quantity index for sugar in 2009 with 2008 as base year
2007 2008 2009
Price Quantity Price Quantity Price Quantity
Coffee (500g) 10.49 13.1 15.99 12.8 17.99 14.2
Sugar (500g) 4.99 17.3 5.29 18.7 7.49 18.2
Milk (1 l) 7.39 48.9 8.99 53.6 9.39 59.2
qn 18.2
Q  100  100  97.3 2.7 % decrease
q0 18.7 10

11. Concept Questions
• 1 – 6, p418, textbook
11

12. Composite index numbers
• Composite index reflect the average change in activity of
a basket of items from the base period to the period
under consideration
– Unweighted composite indices – all items in the
basket is considered to be of the same importance
– Weighted composite indices – each item in the basket
is weighted according to its relative importance
12

13. Unweighted composite index numbers
• Simple composite price index
P
p n
100
p 0
• Simple composite quantity index
Q
q n
100
q 0
13

14. Unweighted composite index numbers - example
• Simple composite quantity index for 2009 with 2007 as base year
2007 2008 2009
Price Quantity Price Quantity Price Quantity
Coffee (500g) 10.49 13.1 15.99 12.8 17.99 14.2
Sugar (500g) 4.99 17.3 5.29 18.7 7.49 18.2
Milk (1 l) 7.39 48.9 8.99 53.6 9.39 59.2
Q
q n
100 
14.2  18.2  59.2
100  115.5 15.5 % inc
q 0 13.1  17.3  48.9 14

15. Unweighted composite index numbers - example
• Simple composite price index for 2008 with 2007 as base year
2007 2008 2009
Price Quantity Price Quantity Price Quantity
Coffee (500g) 10.49 13.1 15.99 12.8 17.99 14.2
Sugar (500g) 4.99 17.3 5.29 18.7 7.49 18.2
Milk (1 l) 7.39 48.9 8.99 53.6 9.39 59.2
P
p n
100 
15.99  5.29  8.99
100  132.4  32.4 % inc
p 0 10.49  4.99  7.39 15

16. Weighted composite index numbers
• Weighted composite price index
P
 p w 100
n
p w 0
• Weighted composite quantity index
Q
 q w 100
n
q w 0
Where: w = weight assigned to each item in the basket
16

17. Weighted composite index numbers - example
• Weighted composite price index for 2008 with 2007 as base
year using the profit for each item as weight
2007 2008 2009
Price Profit Price Profit Price Profit
Coffee (500g) 10.49 70% 15.99 70% 17.99 70%
Sugar (500g) 4.99 30% 5.29 30% 7.49 30%
Milk (1 l) 7.39 20% 8.99 20% 9.39 20%
P
 p w 100
n
p w 0
15.99(.7)  5.29(.3)  8.99(.2)
 100  141.3 41.3 % inc
10.49(.7)  4.99(.3)  7.39(.2) 17

18. Weighted composite index numbers
- Laspeyres approach
• The base period values will be assigned as weights to
the items in the basket
Price index:
• Laspeyres price index weight is the quantity
PL 
 pn q0 100
in the base period
p q0 0
• Laspeyres quantity index Quantity index:
weight is the price
QL 
q pn 0
100 in the base period
q p0 0 18

19. Weighted composite index numbers
- Laspeyres approach
• Advantage is that indices calculated for different period
using the same basket of items may be compared
directly as long as the base period remains unchanged
• Disadvantage is that it over estimates increases in the
prices as times goes by – it is necessary to adjust the
base period from time to time
19

20. Weighted composite index numbers - example
• Laspeyres price index for 2009 with 2007 as base year
2007 2008 2009
Price Quantity Price Quantity Price Quantity
Coffee (500g) 10.49 13.1 15.99 12.8 17.99 14.2
Sugar (500g) 4.99 17.3 5.29 18.7 7.49 18.2
Milk (1 l) 7.39 48.9 8.99 53.6 9.39 59.2
PL 
p qn 0
100 
17.99(13.1)  7.49(17.3)  9.39(48.9)
100
p q0 0 10.49(13.1)  4.99(17.3)  7.39(48.9)
 140.9  40.9 % inc
20

21. Weighted composite index numbers
- Paasche approach
• The consumed current period values will be assigned as
weights to the items in the basket
• Paasche price index Price index:
weight is the quantity
PP 
p q
n n
100 in the current period
p q
0 n
• Paasche quantity index Quantity index:
weight is the price
QP 
q p
n n
100 in the current period
q p
0 n 21

22. Weighted composite index numbers
- Paasche approach
• Advantage is that indices calculated for different period
using the same basket of items may be compared
directly as long as the base period remains unchanged
• Disadvantage is that it over estimates increases in the
prices as times goes by – it is necessary to adjust the
base period from time to time
22

23. Weighted composite index numbers - example
• Paasche quantity index for 2009 with 2007 as base year
2007 2008 2009
Price Quantity Price Quantity Price Quantity
Coffee (500g) 10.49 13.1 15.99 12.8 17.99 14.2
Sugar (500g) 4.99 17.3 5.29 18.7 7.49 18.2
Milk (1 l) 7.39 48.9 8.99 53.6 9.39 59.2
QP 
q pn n
100 
14.2(17.99)  18.2(7.49)  59.2(9.39)
100
q p
0 n
13.1(17.99)  17.3(7.49)  48.9(9.39)
 114.9 14.9 % inc
23

24. Weighted composite index numbers
- Fischer approach
• Fischer price index
PF  PL  PP
• Fischer quantity index
QF  QL  QP
• May only be used if the indices for Laspeyres and Paasche
have the same base period 24

25. Example
The price of bread (rands/bread), meat (rands/kg), Cabbage (rands/cabbage) and wine
(rands/bottle), as well as the quantities (in millions) consumed during 2006, 2007 & 2008
are given in the following table:-
Price Quantity
2006 2007 2008 2006 2007 2008
Bread 7.0 6.6 8.4 900 1000 900
Meat 44.0 46.0 59.0 600 600 700
Cabbage 7.0 7.3 9.6 5 6 5.5
Wine 30.4 30.4 32.1 90 90 100
Calculate the:-
1. Simple quantity index for meat in 2008 with 2006 as base year
2. Simple composite price index for 2007, with 2006 as base year
3. Lapeyres price index for 2008 with 2007 as base year
4. Paasche price index for 2008 with 2007 as base year
5. Fischer price index for 2008 with 2007 as base year
6. Simple composite quantity index for 2008 with 2007 as base year
7. Fischer quantity index for 2007 with 2006 as base year 25

26. EXAMPLE ANSWER
1. 1) Q =
 q  100 = 700  100 = 116.67
n
q 0 600
2) P=
 p  100 = 90.3  100 = 102.15
n
p 0 88.4
3) PL =
 p q  100 = 46146.6  100 = 124.79
n 0
p q 0 036979.8
4) PP =
 p q  100 = 52122.8  100 = 126.45
n n
p q 0 41220.15
n
5) PF = PL  PP = (124.79)(126.45) = 125.62
6) Q =
 q  100 = 1705.5  100 = 100.56
n
q 0 1696
7) QL =
 q p  100 = 36178  100 = 101.99
n 0
q p 0 35471
0
QP =
 q p  100 = 36979.8  100 = 101.84
n n
q p 036312.5
n
26
QF = QL  QP = (101.99)(101.84) = 101.92

27. The index series
• Collection of indices for the same item or basket of items
constructed for a number of consecutive periods using
the same base period
• The base period will be the period = 100
27

28. The index series - example
• Construct an index series for the monthly electricity
usage for a household – use June as base month
Month April May June July August
Useage (kw) 680 754 820 835 798
82.9 92.0 100 101.8 97.3
qnn
q 100  680 100  82.9  17.1% dec
754
Q
Q  100  100  92.0  8 % dec
q00
q 820
820
28

29. Important indices – Consumer price index
• Composite price index of a representative basket of consumer goods
and services
• Serves as a measure of relative change in the prices of services and
goods consumed in SA
• Stats SA publish the CPI monthly
• Price information in the index refers to the first 7 days of that month
• Published in the second half of the next month
• Info used to determine the CPI is obtained from a survey in each of
12 urban areas for each of 3 income groups and contains almost 600
items in 17 categories
29

30. Important indices – Consumer price index
• A weight is assigned to each item in the basket according to their
relative importance
p0 q0
w
 p0 q0
  w pn
p0
CPI 
w
30

31. Important indices – Consumer price index
• CPI is used to determine the inflation rate
• Deflate other value series
• Adjust prices, wages, salaries and other variables for changes in the
inflation rate
• It is available quickly
• A disadvantage is that it is based on a household with on average 1.6
children, takes only certain good and services into account, includes
indirect taxes but excluded direct taxes
• Can use consecutive CPI’s as a time series to make forecasts on
future values and trends
31

32. EXAMPLES OF IMPORTANT INDICES
• JSE all share index
• JSE gold index
• CPI- consumer price index – used to calculate
inflation rate and cost of living
• Inflation rate
• PPI – Production price index
• Business confidence index
• New car sales index
32

33. Statistics SA
• Look at www.stassa.gov.za
33

34. Example
• Activity 1, p197 Module Manual
34

35. Example
• Activity 2, p199 Module Manual
35

36. Classwork/Homework
• Revision exercises 1,2,3 p 200 module
manual
36