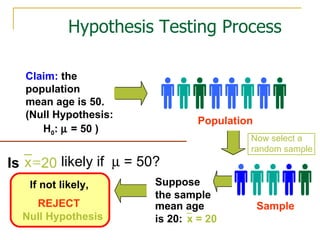
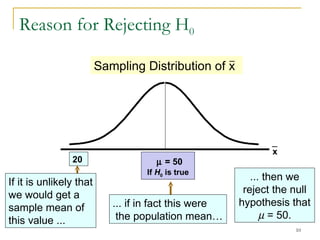
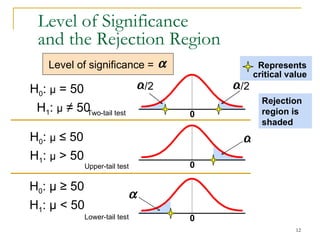
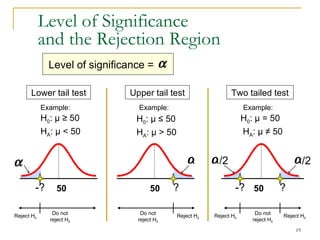
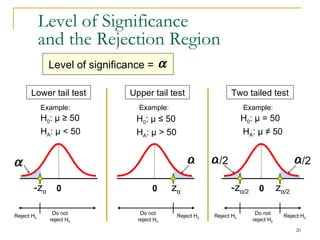
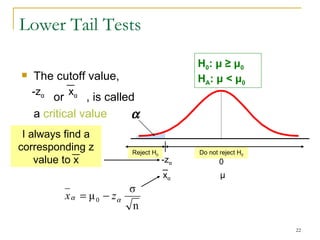
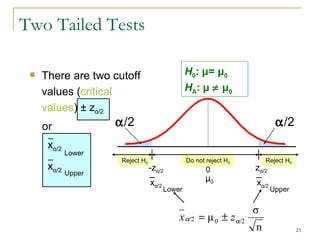
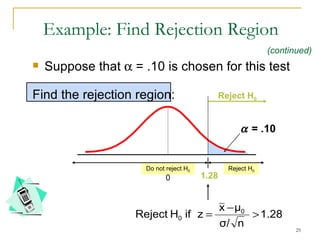
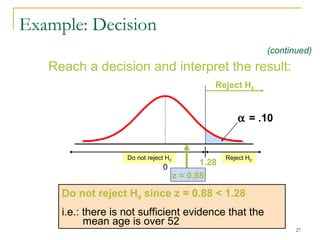
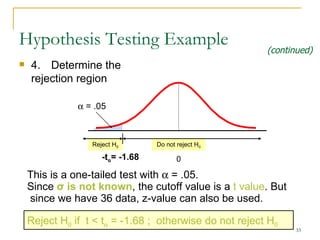
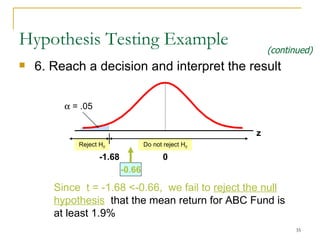
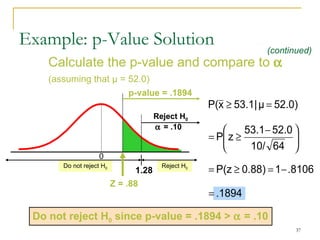
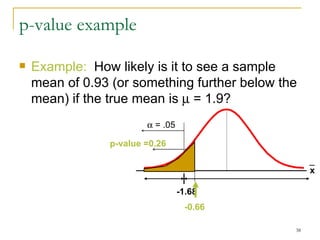
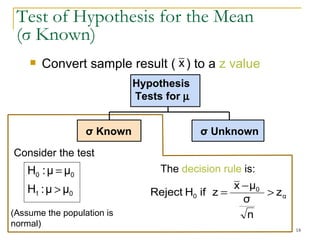
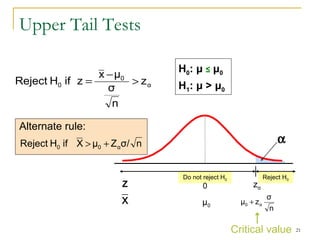
This document provides an introduction to hypothesis testing, including: 1. Defining hypotheses as claims about population parameters and the distinction between the null and alternative hypotheses. 2. Explaining the hypothesis testing process, including specifying the significance level, determining the rejection region, calculating test statistics, and making a decision. 3. Providing examples of one-sample z-tests and t-tests for the mean when the population standard deviation is known and unknown. 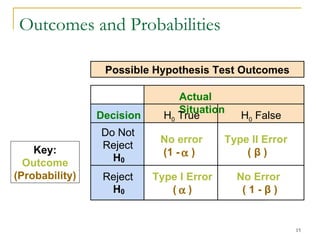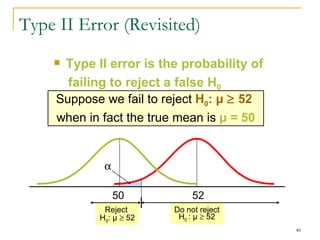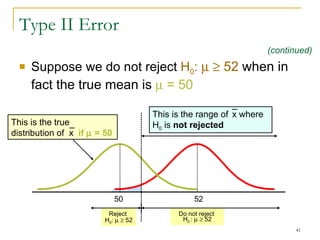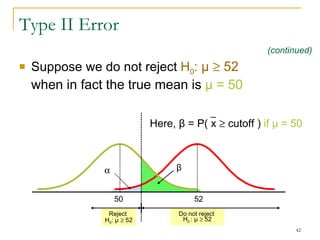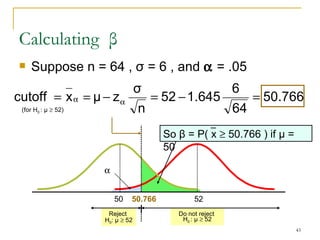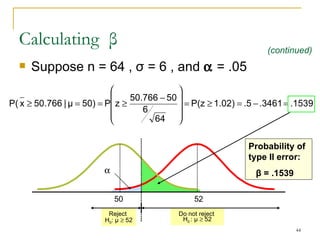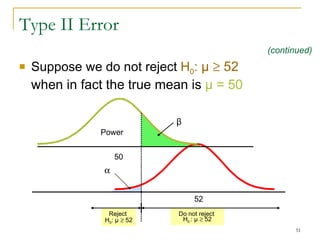4. Discussing type I and type II errors and how significance levels influence the probability of each.

1. Introduction to Hypothesis Testing Istanbul Bilgi University FEC 512 Financial Econometrics-I Asst. Prof. Dr. Orhan Erdem

9. Population Claim: the population mean age is 50. (Null Hypothesis: REJECT Suppose the sample mean age is 20: x = 20 Sample Null Hypothesis 20 likely if  = 50?  Is Hypothesis Testing Process If not likely, Now select a random sample H 0 :  = 50 ) x

10. Reason for Rejecting H 0 Sampling Distribution of x  = 50 If H 0 is true If it is unlikely that we would get a sample mean of this value ... ... then we reject the null hypothesis that  = 50. 20 ... if in fact this were the population mean… x

12. Level of Significance and the Rejection Region H 0 : μ ≥ 50 H 1 : μ < 50 0 H 0 : μ ≤ 50 H 1 : μ > 50   Represents critical value Lower-tail test Level of significance =  0 Upper-tail test Two-tail test Rejection region is shaded /2 0  /2  H 0 : μ = 50 H 1 : μ ≠ 50

15. Outcomes and Probabilities Actual Situation Decision Do Not Reject H 0 No error (1 - )  Type II Error ( β ) Reject H 0 Type I Error ( )  Possible Hypothesis Test Outcomes H 0 False H 0 True Key: Outcome (Probability) No Error ( 1 - β )

19. Level of Significance and the Rejection Region H 0 : μ ≥ 50 H A : μ < 50 50 H 0 : μ ≤ 50 H A : μ > 50 H 0 : μ = 50 H A : μ ≠ 50   /2 Lower tail test Level of significance =  50 /2  Upper tail test Two tailed test 5 0  - ? ? - ? ? Reject H 0 Reject H 0 Reject H 0 Reject H 0 Do not reject H 0 Do not reject H 0 Do not reject H 0 Example: Example: Example:

20. Level of Significance and the Rejection Region H 0 : μ ≥ 50 H A : μ < 50 0 H 0 : μ ≤ 50 H A : μ > 50 H 0 : μ = 50 H A : μ ≠ 50   /2 Lower tail test Level of significance =  0 /2  Upper tail test Two tailed test 0  -z α z α -z α /2 z α /2 Reject H 0 Reject H 0 Reject H 0 Reject H 0 Do not reject H 0 Do not reject H 0 Do not reject H 0 Example: Example: Example:

21. Upper Tail Tests Reject H 0 Do not reject H 0  z α 0 μ 0 H 0 : μ ≤ μ 0 H 1 : μ > μ 0 Critical value Z Alternate rule:

28. Calculating the Test Statistic  Known Large Samples  Unknown Hypothesis Tests for  Small Samples The test statistic is: But is sometimes approximated using a z: (continued)

29. Calculating the Test Statistic  Known Large Samples  Unknown Hypothesis Tests for  Small Samples The test statistic is: (The population must be approximately normal) (continued)