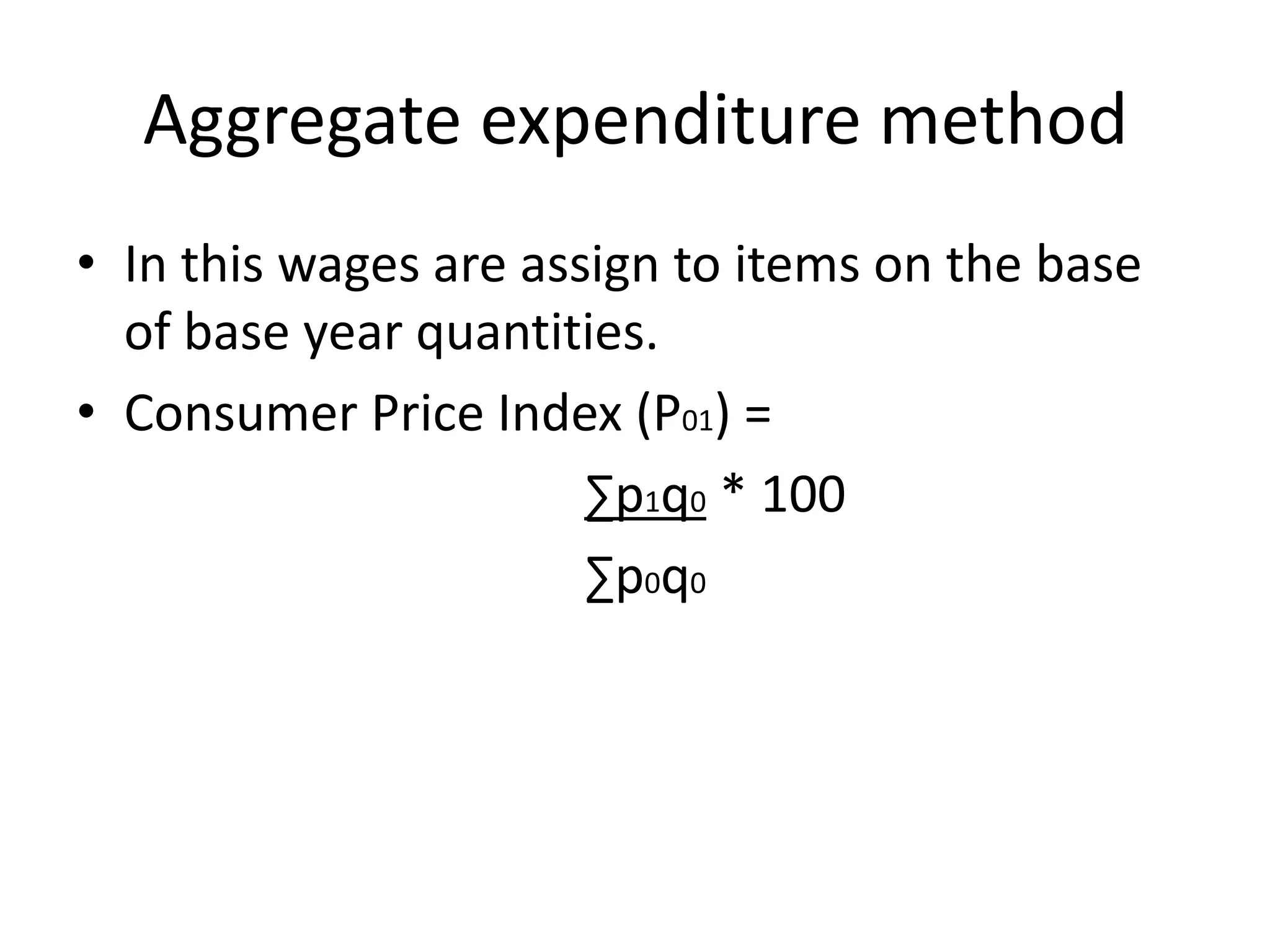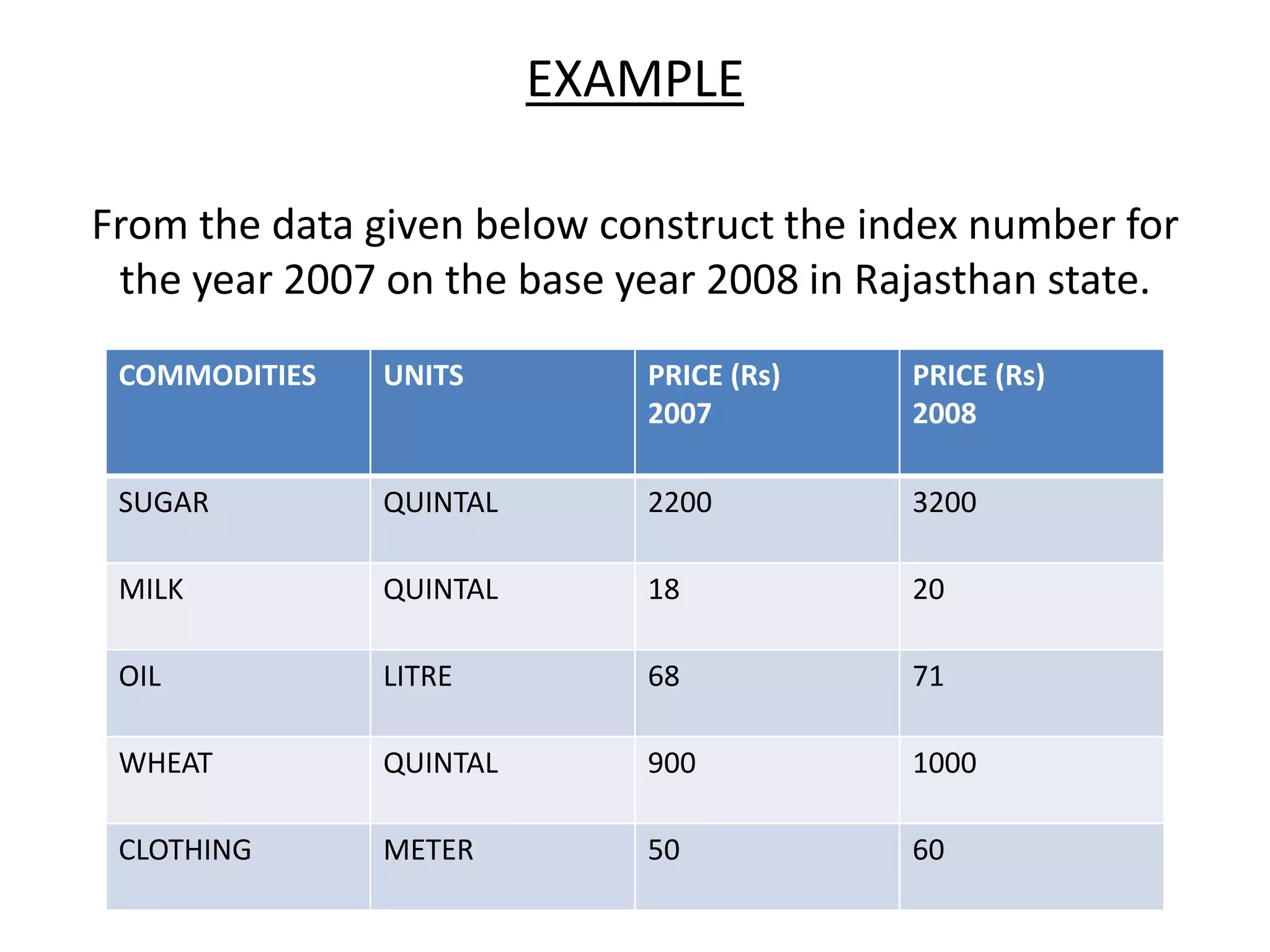
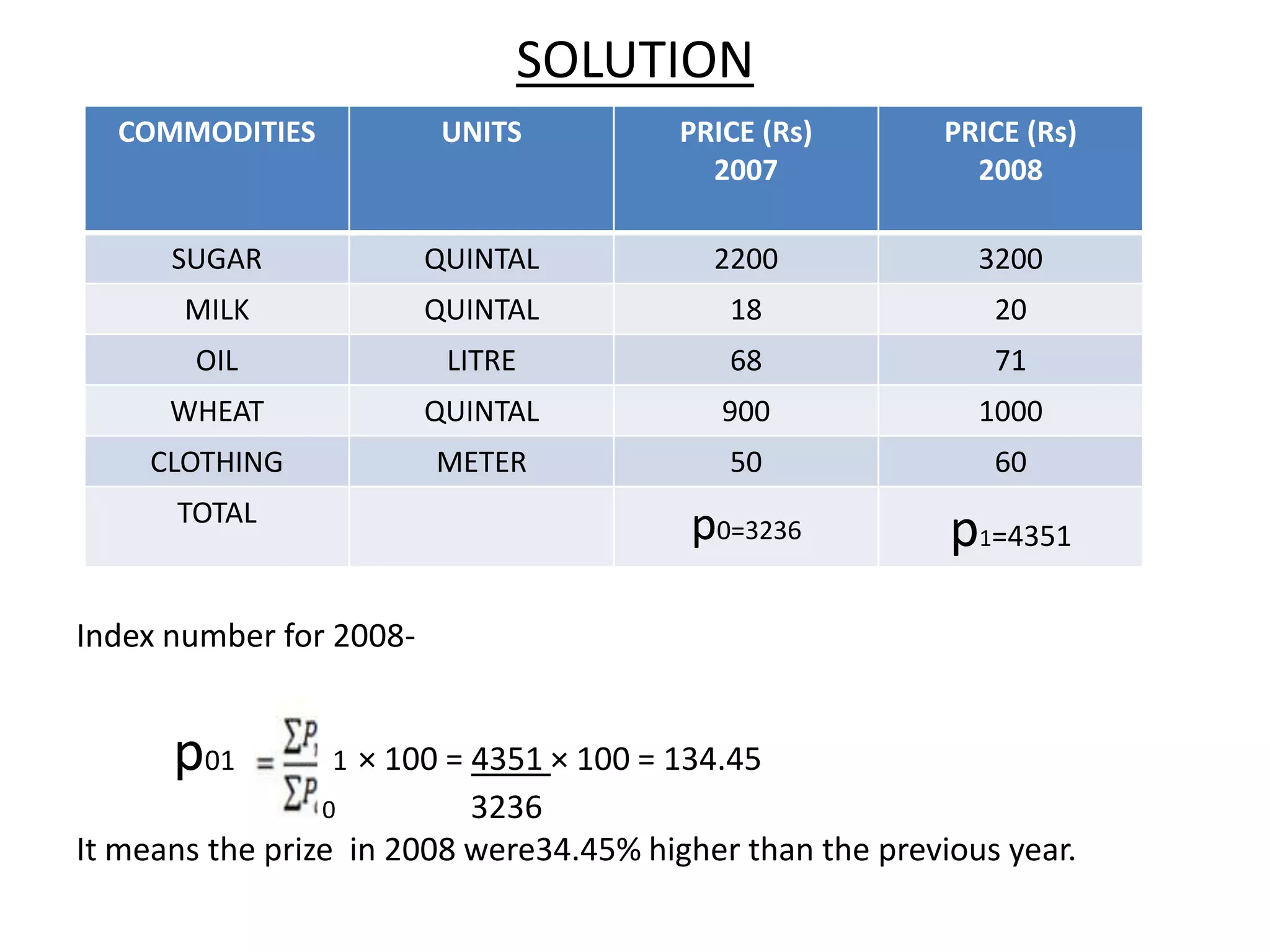
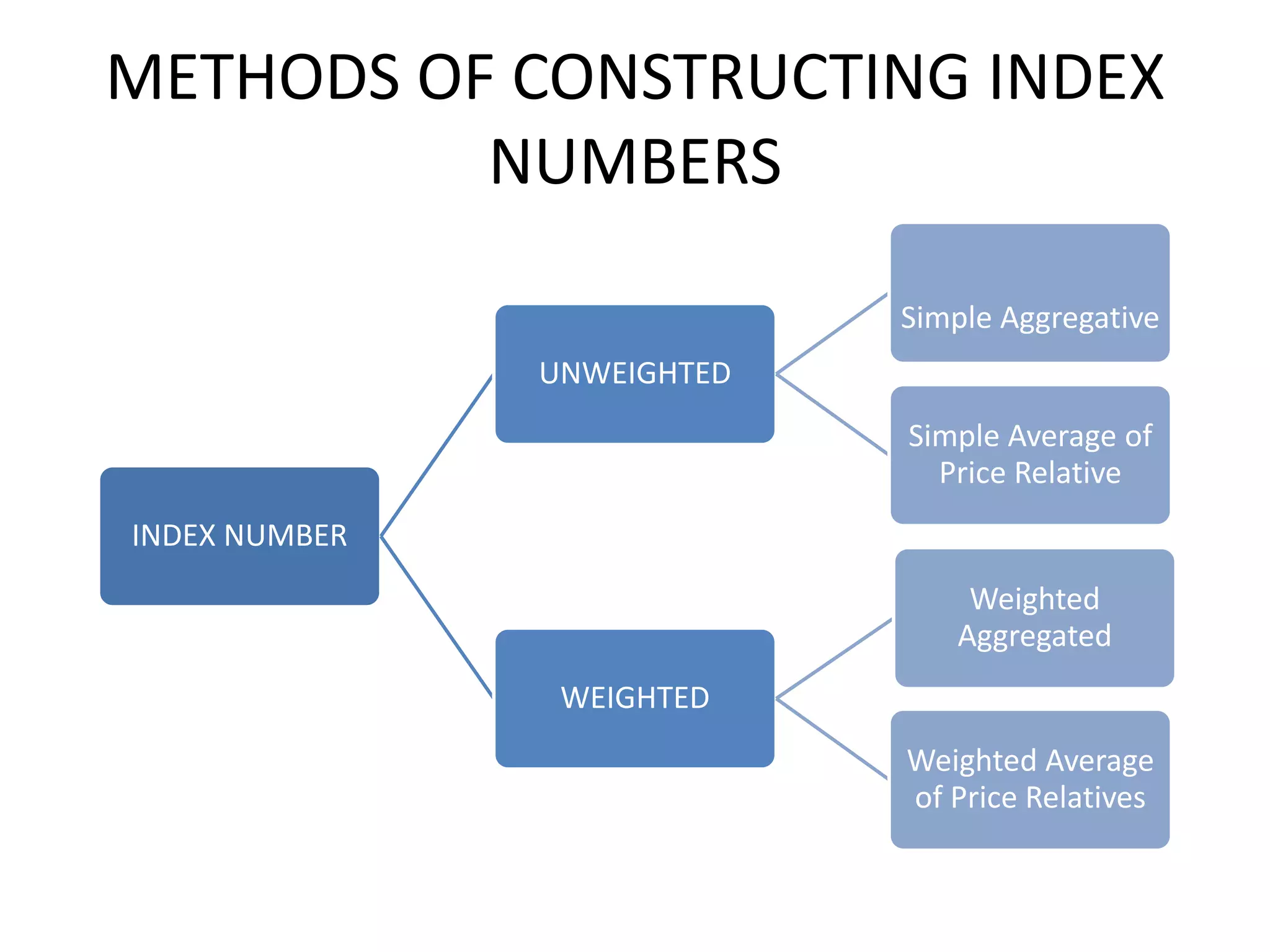
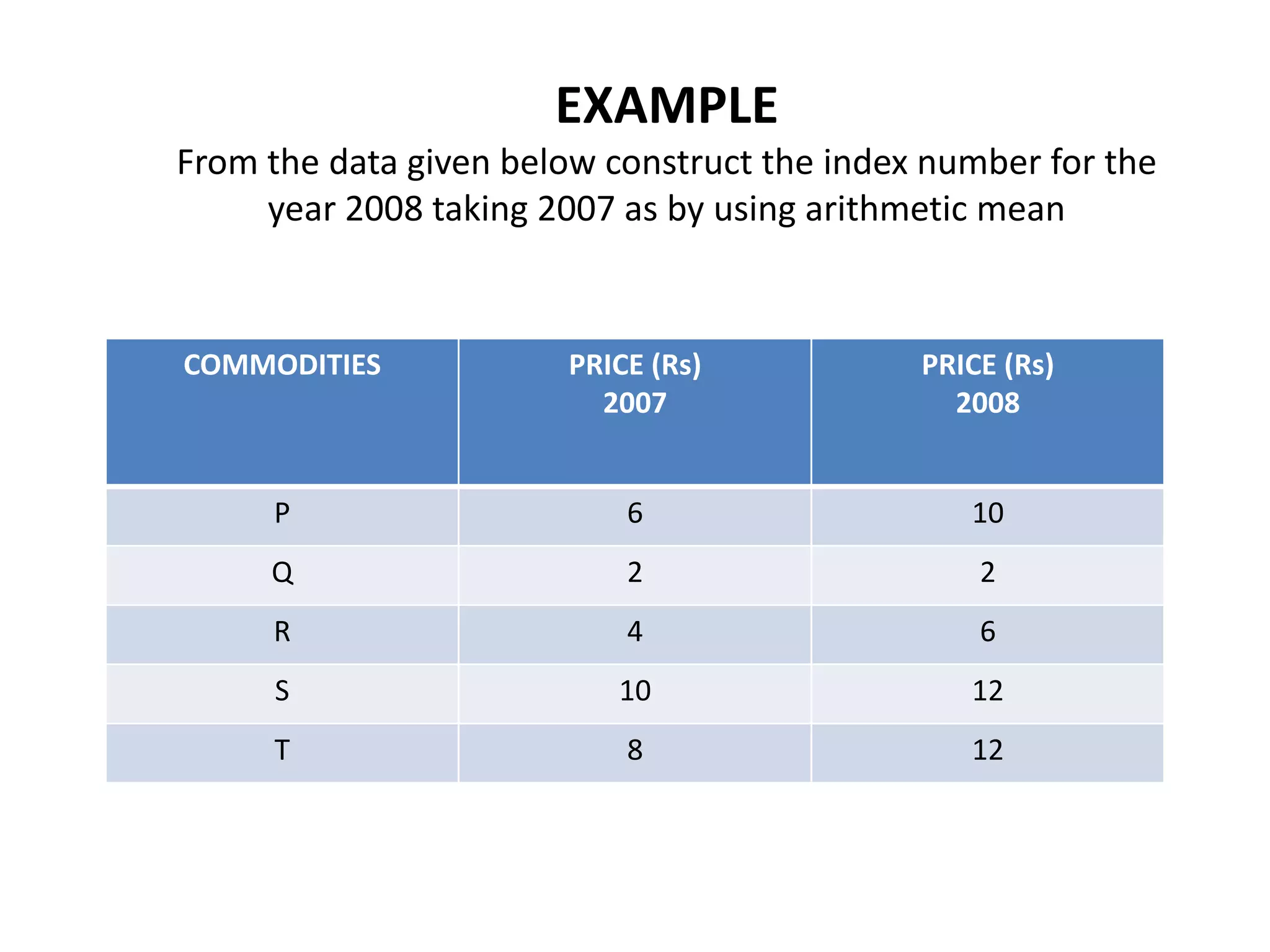
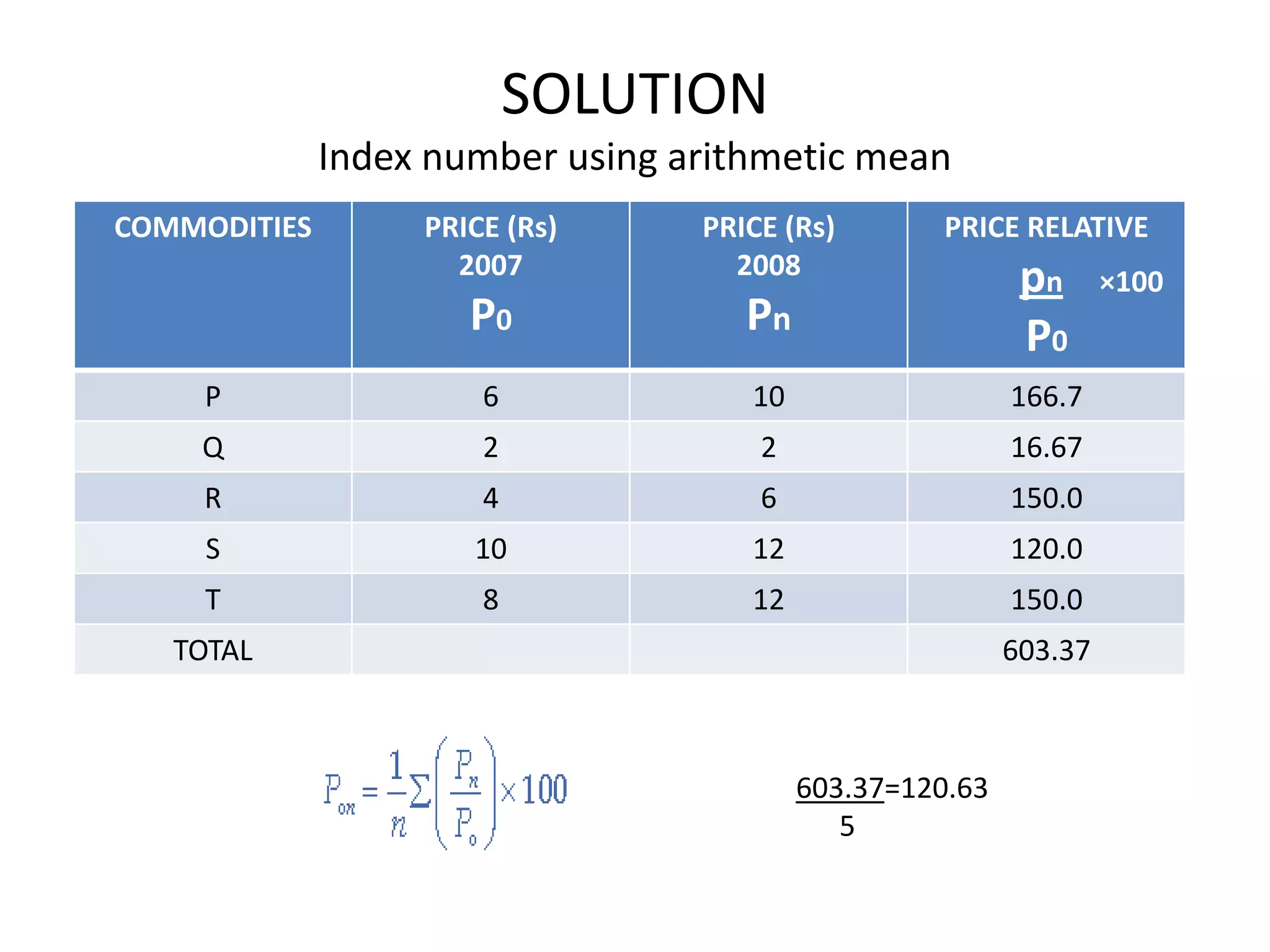
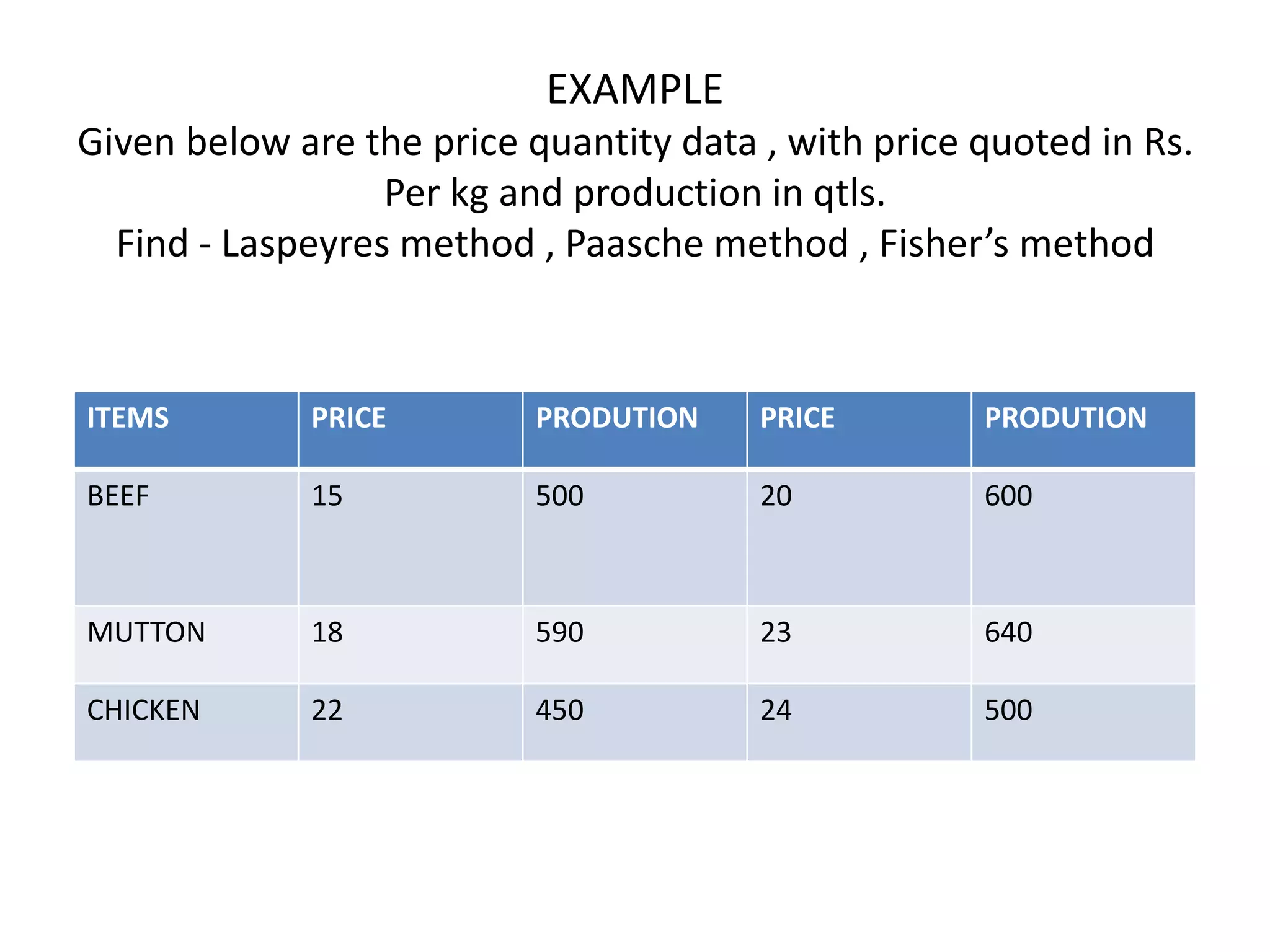
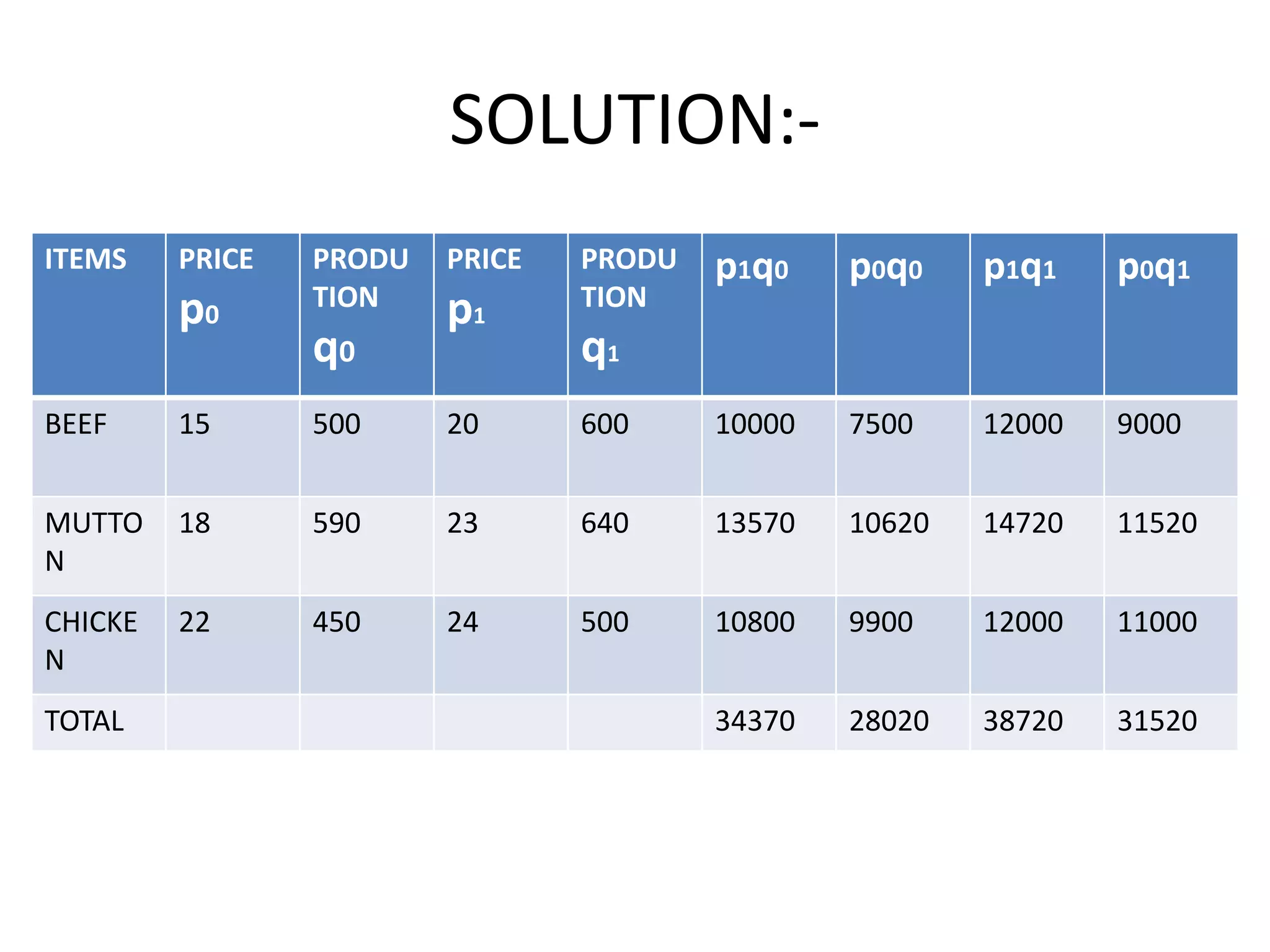
The document provides information on index numbers including: 1) Index numbers measure relative changes in variables like prices, quantities, or values over time by calculating the ratio of current to base values. 2) There are different types of index numbers such as price indexes, quantity indexes, and composite indexes. Methods for constructing indexes include simple aggregative, weighted aggregated, Laspeyres, Paasche, and Fisher's methods. 3) Index numbers have various uses including framing economic policies, revealing trends, and deflating monetary values. Problems in constructing indexes include choosing the base period, averages, commodities, and collecting data.

1. INDEX NUMBER

2. INDEX NUMBER
SUBMITTED TO:- SUBMITTED BY:-
Dr. RENUKA SHARMA ABHISHEK BANSAL
AMAN KASHYAP
TARUN KUMAR
GOURAV CHABBRA

3. INTRODUCTION
•An index number measure the relative
change in price, quantity, value, or some
other item of interest from one time period to
another.
•A simple index number measure the relative
change in one or more than one variable

4. WHAT IS AN INDEX NUMBER
•An index number measure how much a variable
changes over time.
•We calculate the index number by finding the
ratio of the current value to a base value.

5. DEFINITION
“Index numbers are quantitative measures of
growth of prices, production, inventory and
other quantities of economic interest.”

6. CHARACTERISTICS OF INDEX NUMBERS
• Index numbers are specialized averages.
• Index numbers measure the change in the
level of a phenomenon.
• Index number measure the effect of changes
over a period of time.

7. USES OF INDEX NUMBERS
• To framing suitable policies.
• They reveal trends and tendencies.
• Index numbers are very useful in deflating.

8. PROBLEMS RELATED TO INDEX
NUMBERS
• Choice of the base period.
• Choice of an average.
• Choice of index.
• Selection of commodities.
• Data collection.

9. CLASSIFICATION OF INDEX NUMBER
PRICE QUANTITY
INDEX INDEX
VALUE COMPOSITE
INDEX INDEX

10. METHODS OF CONSTRUCTING INDEX
NUMBERS
Simple Aggregative
UNWEIGHTED
Simple Average of
Price Relative
INDEX NUMBER
Weighted
Aggregated
WEIGHTED
Weighted Average
of Price Relatives

11. SIMPLE AGGREGATIVE METHOD
IT consists in expressing the aggregate price of all
commodities in the current year as a percentage of the
year.

12. EXAMPLE
From the data given below construct the index number for
the year 2007 on the base year 2008 in Rajasthan state.
COMMODITIES UNITS PRICE (Rs) PRICE (Rs)
2007 2008
SUGAR QUINTAL 2200 3200
MILK QUINTAL 18 20
OIL LITRE 68 71
WHEAT QUINTAL 900 1000
CLOTHING METER 50 60

13. SOLUTION
COMMODITIES UNITS PRICE (Rs) PRICE (Rs)
2007 2008
SUGAR QUINTAL 2200 3200
MILK QUINTAL 18 20
OIL LITRE 68 71
WHEAT QUINTAL 900 1000
CLOTHING METER 50 60
TOTAL
p0=3236 p1=4351
Index number for 2008-
p01 1 × 100 = 4351 × 100 = 134.45
0 3236
It means the prize in 2008 were34.45% higher than the previous year.

14. SIMPLE AVERAGE OF RELATIVE METHOD
The current year price is expressed as a price relative of the base year
price. These price relatives are then averaged to get the index number .
The average used could be arithmetic mean, geometric mean.
Where n is number of item
When geometric mean is used

15. EXAMPLE
From the data given below construct the index number for the
year 2008 taking 2007 as by using arithmetic mean
COMMODITIES PRICE (Rs) PRICE (Rs)
2007 2008
P 6 10
Q 2 2
R 4 6
S 10 12
T 8 12

16. SOLUTION
Index number using arithmetic mean
COMMODITIES PRICE (Rs) PRICE (Rs) PRICE RELATIVE
2007 2008
pn ×100
P0 Pn P0
P 6 10 166.7
Q 2 2 16.67
R 4 6 150.0
S 10 12 120.0
T 8 12 150.0
TOTAL 603.37
603.37=120.63
5

17. WEIGHTED INDEX NUMBERS
• These are those index number in which rational weights are assigned to
various chains in an explicit fashion .
• Weighted aggregative index numbers.
These index numbers are the simple aggrigative type with the
fundamental diffrence that weights are assigned to the various items
included in the index.
 Laspeyres method
 Paasche method
 Fisher’s method
 Marshall-edgeworth method
 Kelly’s method

18. LASPEYRES METHOD
This method was devised by Laspeyres in 1871. In this method the
weights are determined by quantities in the base.
× 100
PAASCHE METHOD
This method was devised by a German statistician Paasche in 1874.
The weights of current year are used as a base year in constructing
the Paasche’s Index number.
× 100

19. FISHER’S METHOD
Fisher’s method Index number is Geometric mean of the laspeyre’s
and paasche’s Index numbers.
× 100
MARSHALL-EDGEWORTH METHOD
In the index the numerator consists of an aggregate of the current
years price multiplied by the weights of both the base year as well
as the current year.
× 100

20. Kelly’s method
Kelly thinks that a ratio of aggregates with selected weights gives
the base index number
q
q
q refers to the quantities of the which is selected as the base. It may
be any year, either base, year or current year

21. EXAMPLE
Given below are the price quantity data , with price quoted in Rs.
Per kg and production in qtls.
Find - Laspeyres method , Paasche method , Fisher’s method
ITEMS PRICE PRODUTION PRICE PRODUTION
BEEF 15 500 20 600
MUTTON 18 590 23 640
CHICKEN 22 450 24 500

22. SOLUTION:-
ITEMS PRICE PRODU PRICE PRODU p1q0 p0q0 p1q1 p0q1
TION TION
p0 p1
q0 q1
BEEF 15 500 20 600 10000 7500 12000 9000
MUTTO 18 590 23 640 13570 10620 14720 11520
N
CHICKE 22 450 24 500 10800 9900 12000 11000
N
TOTAL 34370 28020 38720 31520

23. Laspeyres method
× 100 34370 × 100 = 122.66
28020
Paasche method
× 100 38720 × 100 = 122.84
31520
Fisher’s method
× 100 = 122.69

24. TEST FOR PERFECTION
1. Time reversal test:- P01 * P10 = 1
2. Factor reversal test:-
P10*Q01= ∑p1q1
∑p0q0
1. Circular test:- P01*P12*P20=1

25. CHAIN BASE INDEX NUMBERS
• Chain base index numbers are those numbers
in which the year immediately preceding the
one is taken as base year.

26. • Link Relatives= Current Year’s Price * 100
Previous Year Price
• Chain Base Index=
Link Relative Of Current Year * Chain Index Of Prev. Year
100

27. Conversion Of Chain Index To
Fixed Base Index
• Current Year FBI=
Current Year’s CBI * Previous Year’s FBI
100

28. BASE SHIFTING
• One of the frequent operation necessary in
the use of index number in changing the base
of an index. It is needed in 2 reasons:-
1. When present base year has become rather
old.
2. When some series are to be compared with
other whose base years are different.

29. SPLICING
• Splicing is a process by which new series of
indices is tied with old index series or old
series of indices is tied with new index series.

30. DEFLATING
• It refers to the correction for price changes in
money wages or money income series.
• REAL WAGE= Money Wage * 100
Price Index
• Real Wage Index No.= Index Of Money Wage
Price Index

31. CONSUMER PRICE INDEX
• It is those numbers which measure the effects
on living conditions of different classes of
consumer for any change in the level of prices
over a period of time.

32. METHODS FOR CONSTRUCTING
CONSUMER PRICE INDEX
1. Aggregate Expenditure Method
2. Family Budget Method

33. Aggregate expenditure method
• In this wages are assign to items on the base
of base year quantities.
• Consumer Price Index (P01) =
∑p1q0 * 100
∑p0q0

34. Family budget method
• In this method weights are assign on the basis
of percentage expenditure on item.
• Consumer price index =
∑ PW
∑W
*W = p0q0

35. THANK YOU