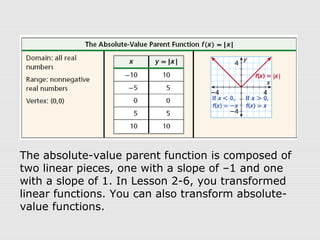
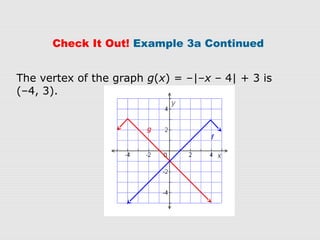
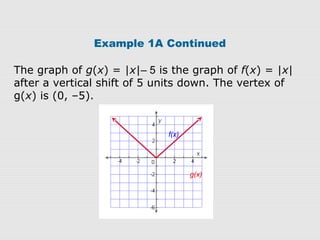
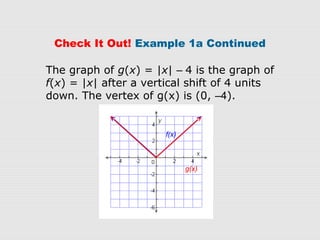
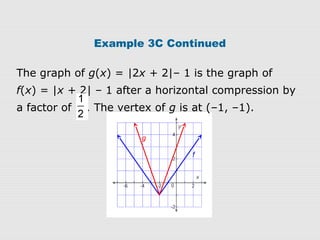
1. Absolute-value functions can be transformed through translations, reflections, stretches, and compressions. Translations move the graph up/down or left/right and change the vertex. Reflections flip the graph across an axis. Stretches and compressions make the graph wider/narrower or taller/shorter. 2. Examples show how to write the rule for a transformed absolute-value function g(x) based on an original function f(x). The transformations can be vertical/horizontal shifts, reflections, or vertical/horizontal stretches/compressions. 3. Graphs confirm that the transformations are applied as expected to f(x), resulting in the graph of g(x) with the

1. Absolute-Value Functions
Warm up
Lesson
Homework

2. Warm Up
Evaluate each expression for f(4) and f(-3).
1. f(x) = –|x + 1|
2. f(x) = 2|x| – 1
3. f(x) = |x + 1| + 2
–5; –2
7; 5
7; 4
Let g(x) be the indicated transformation of
f(x). Write the rule for g(x).
4. f(x) = –2x + 5; vertical translation 6 units down
g(x) = –2x – 1
g(x) = 2x + 8
5. f(x) = x + 2; vertical stretch by a factor of 4

3. Graph and transform absolute-value
functions.
Your Goal Today is…

4. absolute-value function
Vocabulary

5. An absolute-value function is a function whose rule
contains an absolute-value expression. The graph of
the parent absolute-value function f(x) = |x| has a V
shape with a minimum point or vertex at (0, 0).

6. The absolute-value parent function is composed of
two linear pieces, one with a slope of –1 and one
with a slope of 1. In Lesson 2-6, you transformed
linear functions. You can also transform absolute-
value functions.

7. The general forms for translations are
Vertical:
g(x) = f(x) + k
Horizontal:
g(x) = f(x – h)
Remember!

8. Example 1A: Translating Absolute-Value Functions
Perform the transformation on f(x) = |x|.
Then graph the transformed function g(x).
5 units down
Substitute.
The graph of g(x) = |x| – 5 is the graph of f(x) = |x|
after a vertical shift of 5 units down. The vertex of
g(x) is (0, –5).
f(x) = |x|
g(x) = f(x) + k
g(x) = |x| – 5

9. Example 1A Continued
The graph of g(x) = |x|– 5 is the graph of f(x) = |x|
after a vertical shift of 5 units down. The vertex of
g(x) is (0, –5).
f(x)
g(x)

10. Example 1B: Translating Absolute-Value Functions
Perform the transformation on f(x) = |x|.
Then graph the transformed function g(x).
1 unit left
Substitute.
f(x) = |x|
g(x) = f(x – h )
g(x) = |x – (–1)| = |x + 1|

11. Example 1B Continued
f(x)
g(x)
The graph of g(x) = |x + 1| is the graph of
f(x) = |x| after a horizontal shift of 1 unit
left. The vertex of g(x) is (–1, 0).

12. 4 units down
Substitute.
f(x) = |x|
g(x) = f(x) + k
g(x) = |x| – 4
Write In Your Notes! Example 1a
Let g(x) be the indicated transformation of
f(x) = |x|. Write the rule for g(x) and graph
the function.

13. f(x)
g(x)
Check It Out! Example 1a Continued
The graph of g(x) = |x| – 4 is the graph of
f(x) = |x| after a vertical shift of 4 units
down. The vertex of g(x) is (0, –4).

14. Perform the transformation on f(x) = |x|.
Then graph the transformed function g(x).
2 units right
Substitute.
f(x) = |x|
g(x) = f(x – h)
g(x) = |x – 2| = |x – 2|
Write In Your Notes! Example 1b

15. f(x)
g(x)
Check It Out! Example 1b Continued
The graph of g(x) = |x – 2| is the graph of
f(x) = |x| after a horizontal shift of 2 units right.
The vertex of g(x) is (2, 0).

16. Because the entire graph moves when shifted,
the shift from f(x) = |x| determines the vertex
of an absolute-value graph.

17. Example 2: Translations of an Absolute-Value
Function
Translate f(x) = |x| so that the vertex is at
(–1, –3). Then graph.
g(x) = |x – h| + k
g(x) = |x – (–1)| + (–3) Substitute.
g(x) = |x + 1| – 3

18. Example 2 Continued
The graph confirms
that the vertex is (–
1, –3).
f(x)
The graph of g(x) = |x + 1| – 3 is the graph of
f(x) = |x| after a vertical shift down 3 units and
a horizontal shift left 1 unit.
g(x)

19. Write In Your Notes! Example 2
Translate f(x) = |x| so that the vertex is at
(4, –2). Then graph.
g(x) = |x – h| + k
g(x) = |x – 4| + (–2) Substitute.
g(x) = |x – 4| – 2

20. The graph confirms
that the vertex is
(4, –2).
Check It Out! Example 2 Continued
g(x)
The graph of g(x) = |x – 4| – 2 is the graph of
f(x) = |x| after a vertical down shift 2 units and
a horizontal shift right 4 units.
f(x)

21. Reflection across x-axis: g(x) = –f(x)
Reflection across y-axis: g(x) = f(–x)
Remember!
Absolute-value functions can also be stretched,
compressed, and reflected.
Vertical stretch and compression : g(x) = af(x)
Horizontal stretch and compression: g(x) = f
Remember!

22. Example 3A: Transforming Absolute-Value Functions
Perform the transformation. Then graph.
g(x) = f(–x)
g(x) = |(–x) – 2| + 3
Take the opposite of the input value.
Reflect the graph. f(x) =|x – 2| + 3 across the
y-axis.

23. g f
Example 3A Continued
The vertex of the graph g(x) = |–x – 2| + 3 is
(–2, 3).

24. g(x) = af(x)
g(x) = 2(|x| – 1) Multiply the entire function by 2.
Example 3B: Transforming Absolute-Value Functions
Stretch the graph. f(x) = |x| – 1 vertically by a
factor of 2.
g(x) = 2|x| – 2

25. Example 3B Continued
The graph of g(x) = 2|x| – 2 is the graph of
f(x) = |x| – 1 after a vertical stretch by a factor of 2.
The vertex of g is at (0, –2).
f(x) g(x)

26. Example 3C: Transforming Absolute-Value Functions
Compress the graph of f(x) = |x + 2| – 1
horizontally by a factor of .
g(x) = |2x + 2| – 1 Simplify.
Substitute for b.

27. f
The graph of g(x) = |2x + 2|– 1 is the graph of
f(x) = |x + 2| – 1 after a horizontal compression by
a factor of . The vertex of g is at (–1, –1).
Example 3C Continued
g

28. Perform the transformation. Then graph.
g(x) = f(–x)
g(x) = –|–x – 4| + 3
Take the opposite of the input value.
Reflect the graph. f(x) = –|x – 4| + 3 across the
y-axis.
Write In Your Notes! Example 3a
g(x) = –|(–x) – 4| + 3

29. The vertex of the graph g(x) = –|–x – 4| + 3 is
(–4, 3).
Check It Out! Example 3a Continued
f
g

30. Compress the graph of f(x) = |x| + 1 vertically
by a factor of .
Simplify.
Write In Your Notes! Example 3b
g(x) = a(|x| + 1)
g(x) = (|x| + 1)
g(x) = (|x| + )
Multiply the entire function by .

31. Check It Out! Example 3b Continued
f(x)
g(x)
The graph of g(x) = |x| + is the graph of
g(x) = |x| + 1 after a vertical compression by a
factor of . The vertex of g is at ( 0, ).

32. Substitute 2 for b.
Stretch the graph. f(x) = |4x| – 3 horizontally
by a factor of 2.
g(x) = |2x| – 3
Write In Your Notes! Example 3c
Simplify.
g(x) = f( x)
g(x) = | (4x)| – 3

33. Check It Out! Example 3c Continued
g
The graph of g(x) = |2x| – 3 the graph of
f(x) = |4x| – 3 after a horizontal stretch by a factor
of 2. The vertex of g is at (0, –3).
f