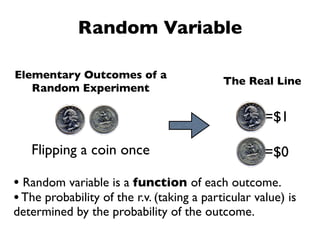
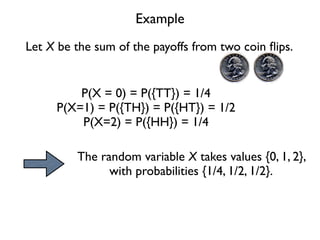
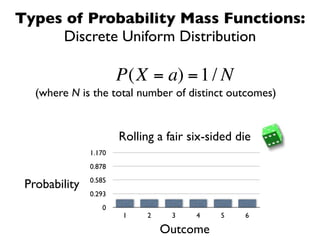
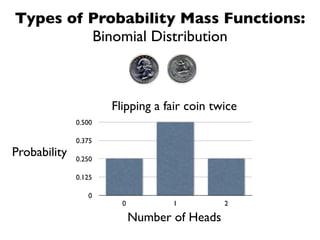
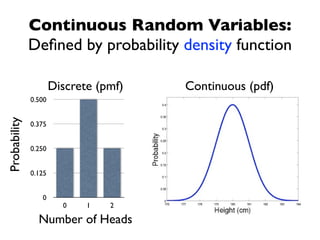
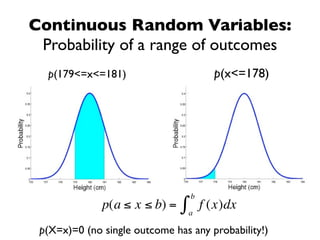
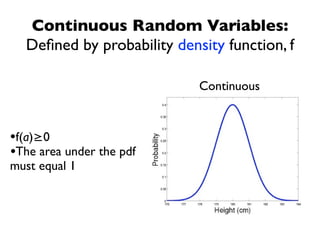
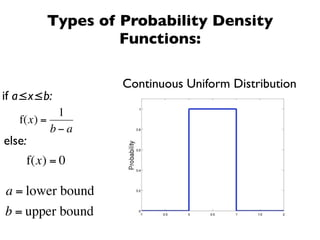
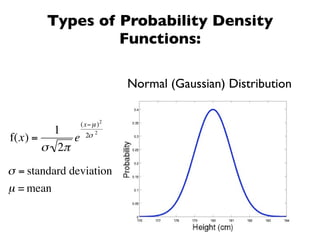
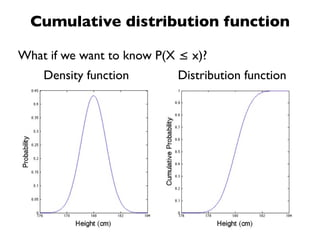
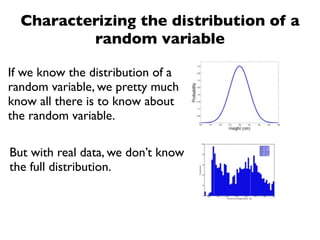
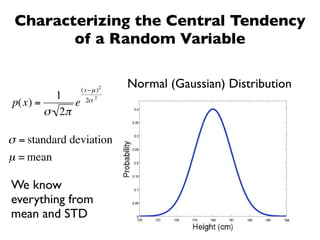
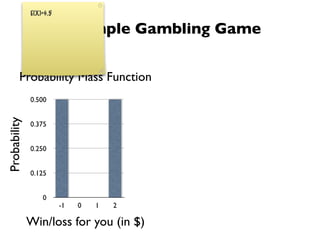
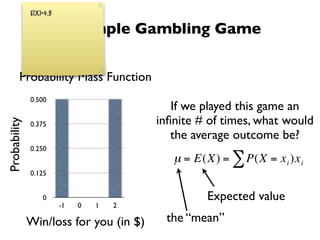
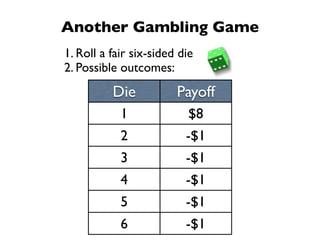
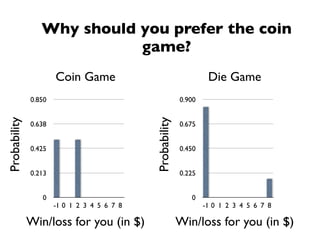
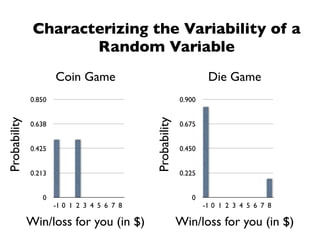
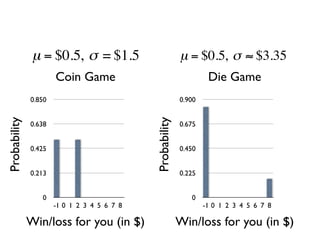
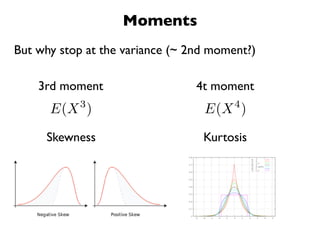
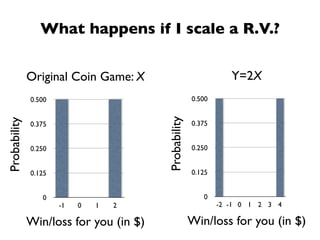
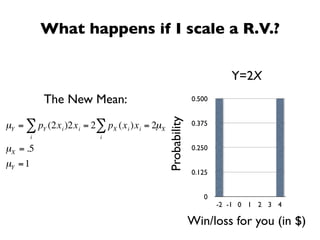
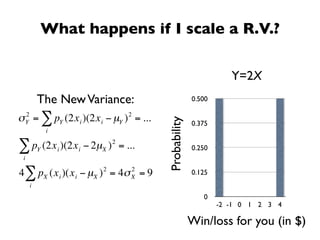
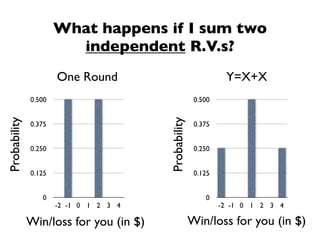
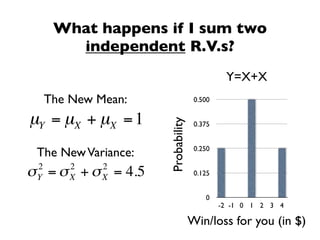
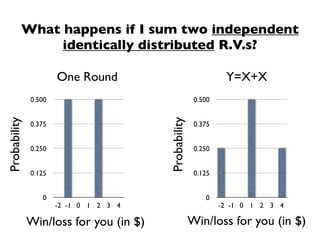
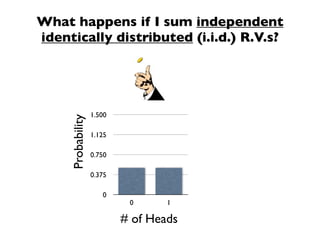
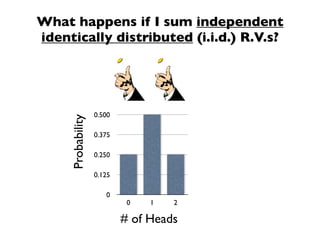
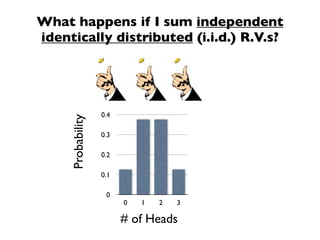
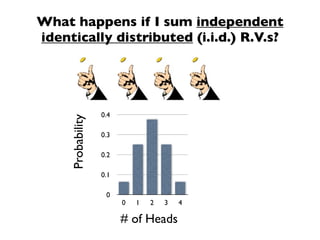
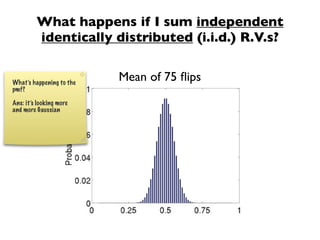
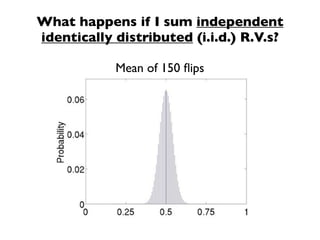
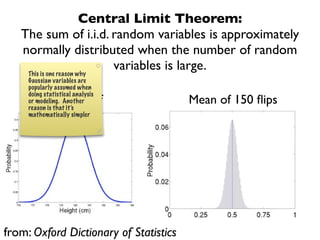
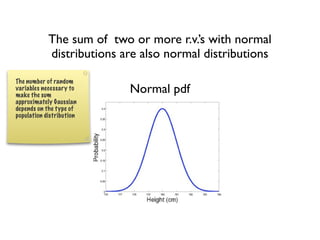
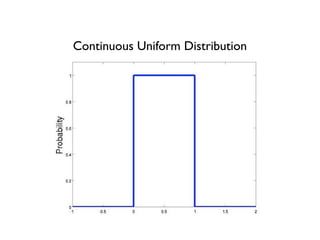
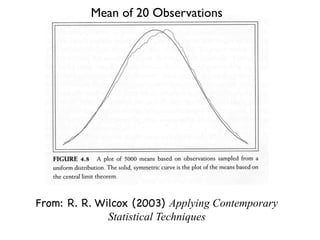
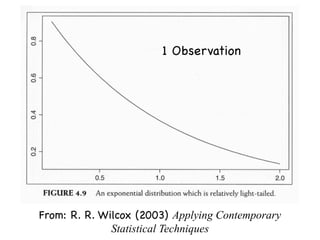
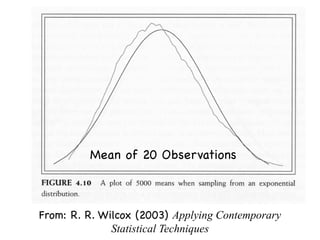
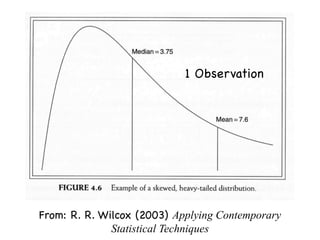
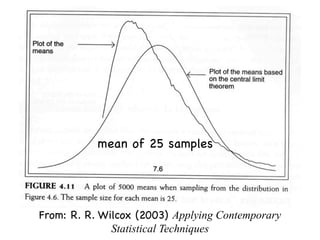
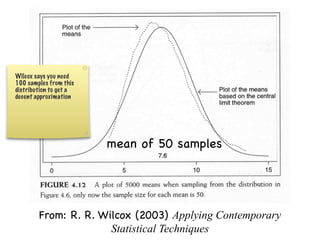
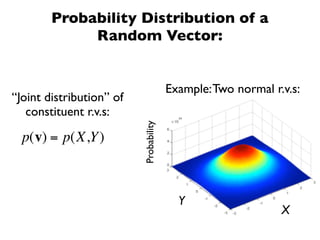
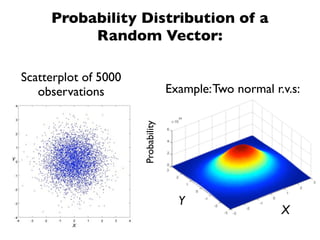
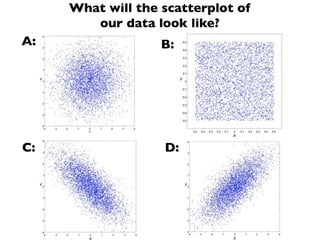
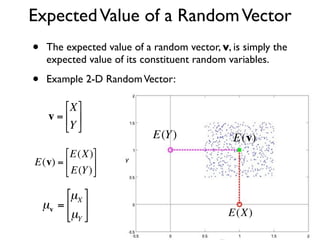
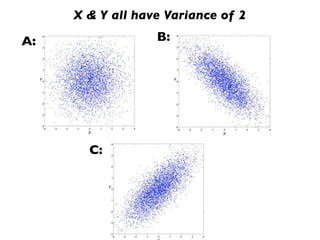
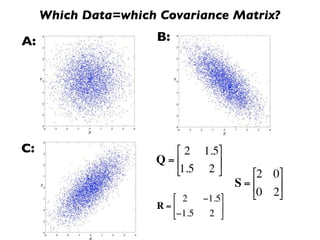
The document discusses random variables and vectors. It defines random variables as functions that assign outcomes of random experiments to real numbers. There are two types of random variables: discrete and continuous. Random variables are characterized by their expected value, variance/standard deviation, and other moments. Random vectors are multivariate random variables. Key concepts covered include probability mass functions, probability density functions, expected value, variance, and how these properties change when random variables are scaled or combined linearly.