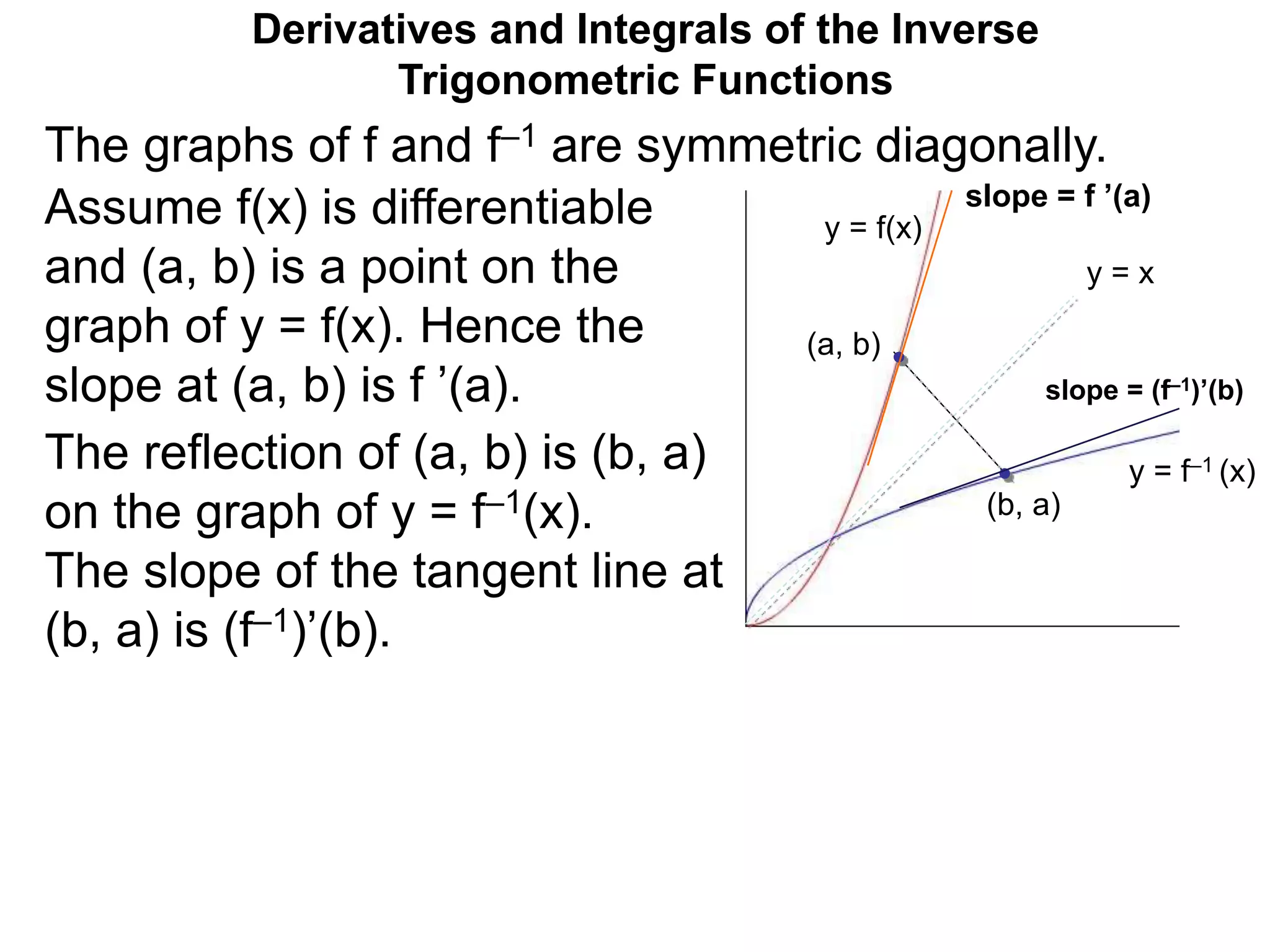
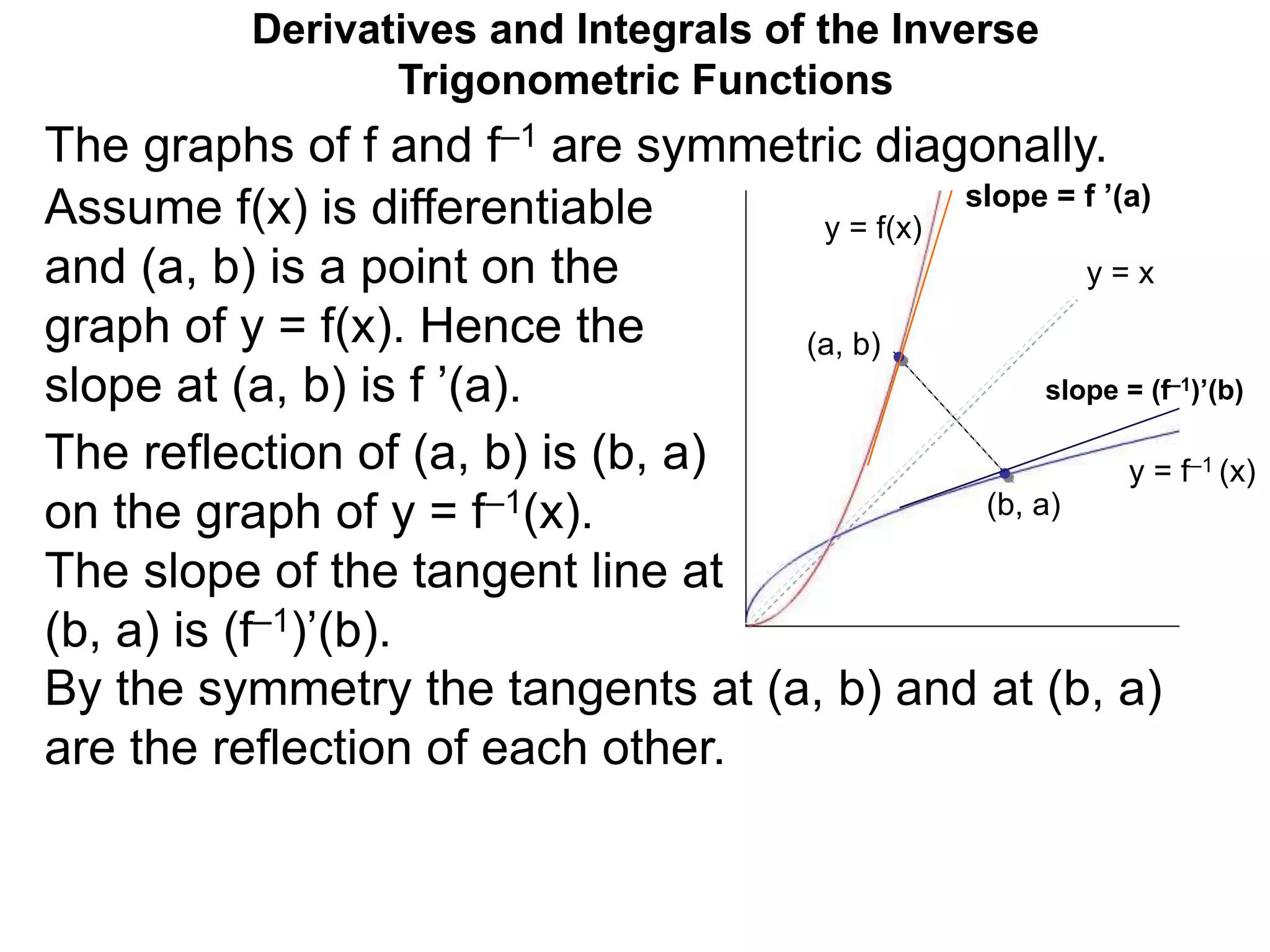
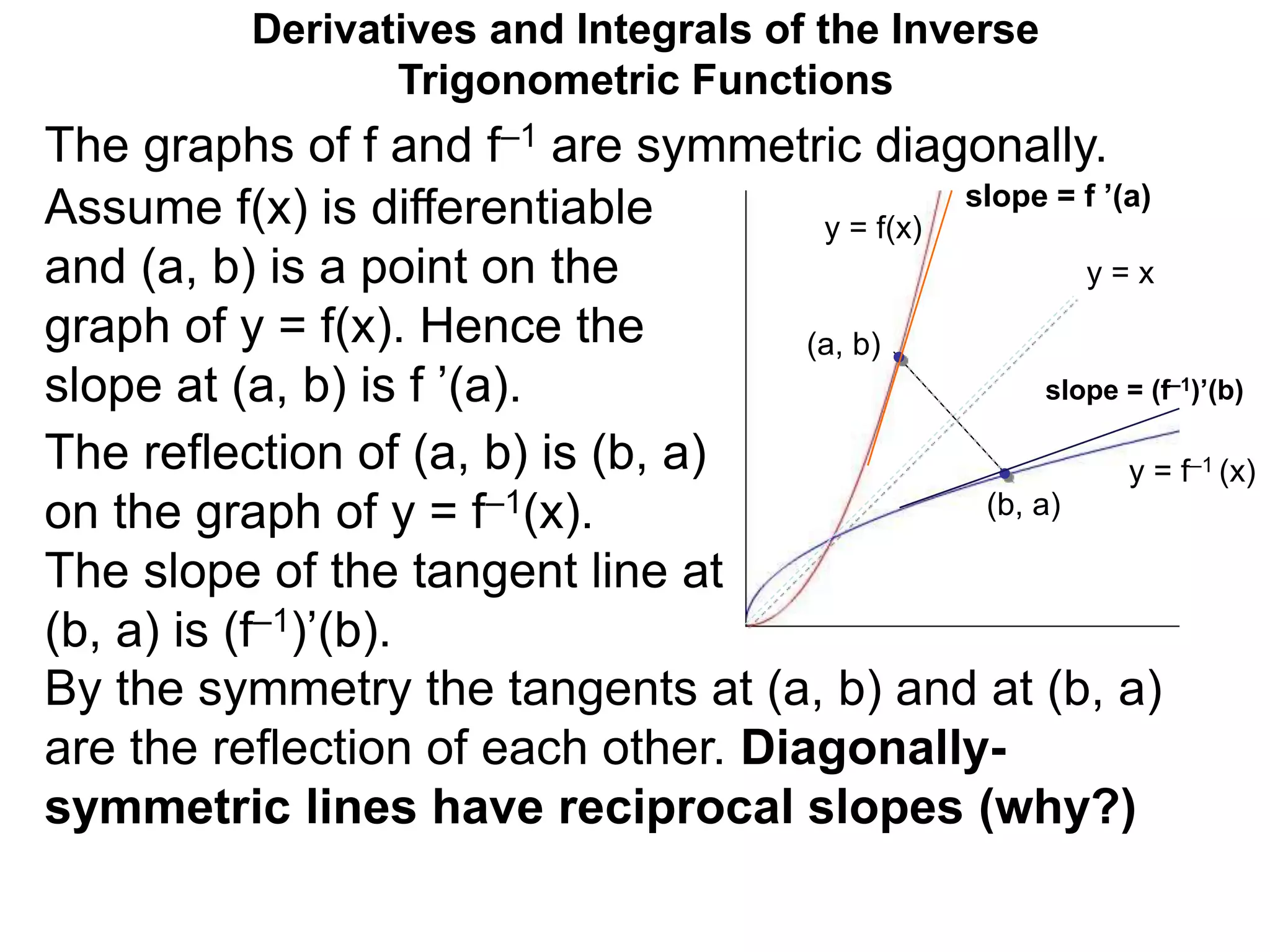
The document discusses the derivatives of inverse trigonometric functions. It shows that if f and f-1 are inverse functions, their graphs are diagonally symmetric and the slopes of their tangent lines at corresponding points (a,b) and (b,a) are reciprocal. It derives formulas for the derivatives of the inverse trig functions arcsin, arccos, arctan, etc. using this property. It then gives examples of computing the derivatives of expressions involving inverse trig functions by applying the chain rule, using the derived formulas.

1. y = f(x)
y = f–1 (x)
The graphs of f and f–1 are symmetric diagonally.
y = x
Derivatives and Integrals of the Inverse
Trigonometric Functions

2. y = f(x)
y = f–1 (x)
The graphs of f and f–1 are symmetric diagonally.
y = x
Derivatives and Integrals of the Inverse
Trigonometric Functions
(a, b)
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x).

3. y = f(x)
y = f–1 (x)
The graphs of f and f–1 are symmetric diagonally.
y = x
Derivatives and Integrals of the Inverse
Trigonometric Functions
(a, b)
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x). Hence the
slope at (a, b) is f ’(a).
slope = f ’(a)

4. y = f(x)
y = f–1 (x)
The graphs of f and f–1 are symmetric diagonally.
y = x
Derivatives and Integrals of the Inverse
Trigonometric Functions
(a, b)
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x). Hence the
slope at (a, b) is f ’(a).
(b, a)
slope = f ’(a)
The reflection of (a, b) is (b, a)
on the graph of y = f–1(x).

5. y = f(x)
y = f–1 (x)
The graphs of f and f–1 are symmetric diagonally.
y = x
Derivatives and Integrals of the Inverse
Trigonometric Functions
(a, b)
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x). Hence the
slope at (a, b) is f ’(a).
(b, a)
slope = f ’(a)
The reflection of (a, b) is (b, a)
on the graph of y = f–1(x).
The slope of the tangent line at
(b, a) is (f–1)’(b).
slope = (f–1)’(b)

6. The graphs of f and f–1 are symmetric diagonally.
Derivatives and Integrals of the Inverse
Trigonometric Functions
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x). Hence the
slope at (a, b) is f ’(a).
The reflection of (a, b) is (b, a)
on the graph of y = f–1(x).
The slope of the tangent line at
(b, a) is (f–1)’(b).
By the symmetry the tangents at (a, b) and at (b, a)
are the reflection of each other.
y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)
slope = (f–1)’(b)

7. The graphs of f and f–1 are symmetric diagonally.
Derivatives and Integrals of the Inverse
Trigonometric Functions
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x). Hence the
slope at (a, b) is f ’(a).
The reflection of (a, b) is (b, a)
on the graph of y = f–1(x).
The slope of the tangent line at
(b, a) is (f–1)’(b).
By the symmetry the tangents at (a, b) and at (b, a)
are the reflection of each other. Diagonally-
symmetric lines have reciprocal slopes (why?)
y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)
slope = (f–1)’(b)

8. The graphs of f and f–1 are symmetric diagonally.
Derivatives and Integrals of the Inverse
Trigonometric Functions
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x). Hence the
slope at (a, b) is f ’(a).
The reflection of (a, b) is (b, a)
on the graph of y = f–1(x).
The slope of the tangent line at
(b, a) is (f–1)’(b).
By the symmetry the tangents at (a, b) and at (b, a)
are the reflection of each other. Diagonally-
symmetric lines have reciprocal slopes (why?)
y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)
slope = (f–1)’(b)
Hence of (f–1)’(b) = 1
f ’(a)

9. The graphs of f and f–1 are symmetric diagonally.
Derivatives and Integrals of the Inverse
Trigonometric Functions
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x). Hence the
slope at (a, b) is f ’(a).
The reflection of (a, b) is (b, a)
on the graph of y = f–1(x).
The slope of the tangent line at
(b, a) is (f–1)’(b).
By the symmetry the tangents at (a, b) and at (b, a)
are the reflection of each other. Diagonally-
symmetric lines have reciprocal slopes (why?)
y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)
slope = (f–1)’(b)
Hence of (f–1)’(b) = 1 = 1
f ’(f–1(b))f ’(a)

10. Suppose f and g are a pair of inverse functions,
then (f o g)(x) = x.
Derivatives and Integrals of the Inverse
Trigonometric Functions

11. Suppose f and g are a pair of inverse functions,
then (f o g)(x) = x.
Differentiate both sides with respect to x and use
the chain rule:
[(f o g)(x)]' = x'
Derivatives and Integrals of the Inverse
Trigonometric Functions

12. Suppose f and g are a pair of inverse functions,
then (f o g)(x) = x.
Differentiate both sides with respect to x and use
the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
Derivatives and Integrals of the Inverse
Trigonometric Functions

13. Suppose f and g are a pair of inverse functions,
then (f o g)(x) = x.
Differentiate both sides with respect to x and use
the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
or
g'(x) = 1
f '(g(x))
Derivatives and Integrals of the Inverse
Trigonometric Functions

14. Suppose f and g are a pair of inverse functions,
then (f o g)(x) = x.
Differentiate both sides with respect to x and use
the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
or
g'(x) = 1
f '(g(x))
Set f = sin(x) and g = arcsin(x)
Derivatives and Integrals of the Inverse
Trigonometric Functions

15. Suppose f and g are a pair of inverse functions,
then (f o g)(x) = x.
Differentiate both sides with respect to x and use
the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
or
g'(x) = 1
f '(g(x))
Set f = sin(x) and g = arcsin(x) we obtain
[arcsin(x)]' = 1
dsin(y)
Derivatives and Integrals of the Inverse
Trigonometric Functions
dy y=arcsin(x)

16. Suppose f and g are a pair of inverse functions,
then (f o g)(x) = x.
Differentiate both sides with respect to x and use
the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
or
g'(x) = 1
f '(g(x))
Set f = sin(x) and g = arcsin(x) we obtain
[arcsin(x)]' = 1
dsin(y)
1
cos(arcsin(x))
=
Derivatives and Integrals of the Inverse
Trigonometric Functions
dy y=arcsin(x)

17. [arcsin(x)]'
1
cos(arcsin(x))
=
Derivatives and Integrals of the Inverse
Trigonometric Functions

18. θ=arcsin(x)
x
1
[arcsin(x)]'
1
cos(arcsin(x))
=
Derivatives and Integrals of the Inverse
Trigonometric Functions

19. θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
Derivatives and Integrals of the Inverse
Trigonometric Functions

20. θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
1
1 – x2
[arcsin(x)]' =
Derivatives and Integrals of the Inverse
Trigonometric Functions

21. θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
1
1 – x2
[arcsin(x)]' =
Derivatives and Integrals of the Inverse
Trigonometric Functions
–1 1
–π/2
π/2
x
y=arcsin(x)

22. θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
1
1 – x2
[arcsin(x)]' =
We use the same technique to obtain the
derivatives of the other inverse trig-functions.
Derivatives and Integrals of the Inverse
Trigonometric Functions
–1 1
–π/2
π/2
x
y=arcsin(x)

23. θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
1
1 – x2
[arcsin(x)]' =
We use the same technique to obtain the
derivatives of the other inverse trig-functions.
Derivatives and Integrals of the Inverse
Trigonometric Functions
–1 1
–π/2
π/2
x
y=arcsin(x)
We display the graphs of each inverse–trig and
list each of their derivatives below.

24. Derivatives of the Inverse Trig–Functions
1
1 – x2
[sin–1(x)] ' =
y =sin–1(x)

25. Derivatives of the Inverse Trig–Functions
[cos–1(x)]' =
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
y =sin–1(x)
y =cos–1(x)

26. Derivatives of the Inverse Trig–Functions
[cos–1(x)]' =
1
1 + x2
[tan–1(x)]' =
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
y =tan–1(x)
y =sin–1(x)
y =cos–1(x)

27. Derivatives of the Inverse Trig–Functions
[cos–1(x)]' =
1
1 + x2
[tan–1(x)]' =
–1
1 + x2[cot–1(x)]' =
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
y =tan–1(x)
y =sin–1(x)
y =cos–1(x)
y =cot–1(x)

28. Derivatives of the Inverse Trig–Functions
[cos–1(x)]' =
1
1 + x2
[tan–1(x)]' =
|x|x2 – 1
[sec–1(x)]' =
–1
1 + x2[cot–1(x)]' =
y =sec–1(x)
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
1
y =tan–1(x)
y =sin–1(x)
y =cos–1(x)
y =cot–1(x)

29. Derivatives of the Inverse Trig–Functions
[cos–1(x)]' =
1
1 + x2
[tan–1(x)]' =
|x|x2 – 1
[sec–1(x)]' =
–1
1 + x2[cot–1(x)]' =
–1
|x|x2 – 1
[csc–1(x)]' =
y =sec–1(x) y =csc–1(x)
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
1
y =tan–1(x)
y =sin–1(x)
y =cos–1(x)
y =cot–1(x)

30. Derivatives of the Inverse Trig–Functions
u'
1 – u2[sin–1(u)]' = –u'
1 – u2
[cos–1 (u)]' =
u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
–u'
1 + u2[cot–1(u)]' =
–u'
|u|u2 – 1
[csc–1(u)]' =
dsin-1(u)
dx
= 1
1 – u2
du
dx
–1
1 – u2
du
dx
1
1 + u2
du
dx
1
|u|u2 – 1
du
dx
dcos-1(u)
dx
=
dtan-1(u)
dx
=
dsec-1(u)
dx
=
–1
1 + u2
du
dx
dtan-1(u)
dx
=
–1
|u|u2 – 1
du
dx
dcsc-1(u)
dx
=
Below are the chain–rule versions where u = u(x).

31. Derivatives and Integrals of the Inverse
Trigonometric Functions
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.

32. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
Example A. Find the following derivatives.
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
2
c. sec–1(ln(x))

33. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
2
Example A. Find the following derivatives.
Set u = x3,
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
c. sec–1(ln(x))

34. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
2
Example A. Find the following derivatives.
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
c. sec–1(ln(x))

35. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
2
Example A. Find the following derivatives.
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
c. sec–1(ln(x))

36. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
Set u = ex,
2
Example A. Find the following derivatives.
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
c. sec–1(ln(x))

37. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
Set u = ex, so [cos-1(ex )]' =
2
2
1 – (ex )2
–(ex )'
2
2
Example A. Find the following derivatives.
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
c. sec–1(ln(x))

38. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
Set u = ex, so [cos-1(ex )]' =
2
2
1 – (ex )2
–(ex )'
2
2
=
–2xex
1 – e2x2
2
Example A. Find the following derivatives.
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
c. sec–1(ln(x))

39. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
Set u = ex, so [cos-1(ex )]' =
2
2
1 – (ex )2
–(ex )'
2
2
=
–2xex
1 – e2x2
2
Set u = ln(x), so [sec–1(ln(x)]'
=
Example A. Find the following derivatives.
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
c. sec–1(ln(x))

40. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
Set u = ex, so [cos-1(ex )]' =
2
2
1 – (ex )2
–(ex )'
2
2
=
–2xex
1 – e2x2
2
c. sec–1(ln(x))
Set u = ln(x), so [sec–1(ln(x)]'
=
1/x
|ln(x)|ln2(x) – 1
Example A. Find the following derivatives.
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.

41. Derivatives and Integrals of the Inverse
Trigonometric Functions
b. cos–1(ex )
Set u = ex, so [cos-1(ex )]' =
2
2
1 – (ex )2
–(ex )'
2
2
=
–2xex
1 – e2x2
2
Set u = ln(x), so [sec–1(ln(x)]'
=
1/x
|ln(x)|ln2(x) – 1
= 1
x|ln(x)||ln2(x) – 1
Example A. Find the following derivatives.
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.
c. sec–1(ln(x))

42. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫

43. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫
= cos-1(u) + C
1 – u2
- du
∫

44. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2

45. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
|u|u2 – 1
Expressing the relations in integrals:
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
du

46. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Example B. Find the integral ∫
dx
9 + 4x2
|u|u2 – 1
du

47. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Match the form of the integral to the one for tan-1(u).
|u|u2 – 1
du
Example B. Find the integral ∫
dx
9 + 4x2

48. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Match the form of the integral to the one for tan-1(u).
Write 9 + 4x2 = 9 (1 + x2)
4
9
|u|u2 – 1
du
Example B. Find the integral ∫
dx
9 + 4x2

49. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Match the form of the integral to the one for tan-1(u).
Write 9 + 4x2 = 9 (1 + x2) = 9 [1 + ( x)2]2
3
4
9
|u|u2 – 1
du
Example B. Find the integral ∫
dx
9 + 4x2

50. Derivatives and Integrals of the Inverse
Trigonometric Functions
= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Match the form of the integral to the one for tan-1(u).
Write 9 + 4x2 = 9 (1 + x2) = 9 [1 + ( x)2]2
3
4
9
Hence dx
9 + 4x2∫ = dx
1 + ( x)2∫
1
9 2
3
|u|u2 – 1
du
Example B. Find the integral ∫
dx
9 + 4x2

51. Derivatives and Integrals of the Inverse
Trigonometric Functions
dx
1 + ( x)2∫
1
9 2
3
substitution method

52. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x
substitution method

53. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
substitution method

54. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
substitution method

55. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
= ∫
1
9
1
1 + u2
3
2
du
substitution method

56. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
= ∫
1
9
1
1 + u2
3
2
du
= ∫
1
6
1
1 + u2 du
substitution method

57. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
= ∫
1
9
1
1 + u2
3
2
du
= ∫
1
6
1
1 + u2 du
= tan-1(u) + C
1
6
substitution method

58. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
= ∫
1
9
1
1 + u2
3
2
du
= ∫
1
6
1
1 + u2 du
= tan-1(u) + C
1
6
= tan-1( x) + C
1
6
2
3
substitution method

59. Derivatives and Integrals of the Inverse
Trigonometric Functions
ex
∫Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)

60. Derivatives and Integrals of the Inverse
Trigonometric Functions
ex
∫Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)

61. Derivatives and Integrals of the Inverse
Trigonometric Functions
ex
∫
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)

62. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
ex
∫ 1 – e2x
dx
0
ln(1/2)

63. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex ex
ex
∫ 1 – e2x
dx
0
ln(1/2)

64. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex ex
ex
∫ 1 – e2x
dx
0
ln(1/2)

65. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
ex
∫ 1 – e2x
dx
0
ln(1/2)

66. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1

67. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2

68. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
ex

69. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex

70. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2

71. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2
= sin-1(u) |
1/2
1

72. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2
= sin-1(u) |
1/2
1
= sin-1(1) – sin-1(1/2)

73. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2
= sin-1(u) |
1/2
1
= sin-1(1) – sin-1(1/2) = π/2 – π/6

74. Derivatives and Integrals of the Inverse
Trigonometric Functions
Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2
= sin-1(u) |
1/2
1
= sin-1(1) – sin-1(1/2) = π/2 – π/6 = π/3

75. Lastly, we have the hyperbolic trigonometric
functions.
Derivatives and Integrals of the Inverse
Trigonometric Functions

76. Lastly, we have the hyperbolic trigonometric
functions. These functions are made from the
exponential functions with relations among
them that are similar to the trig-family.
Derivatives and Integrals of the Inverse
Trigonometric Functions

77. Derivatives and Integrals of the Inverse
Trigonometric Functions
We define the hyperbolic sine as
sinh(x) = (pronounced as "sinch of x").
ex – e-x
2
Lastly, we have the hyperbolic trigonometric
functions. These functions are made from the
exponential functions with relations among
them that are similar to the trig-family.

78. Derivatives and Integrals of the Inverse
Trigonometric Functions
We define the hyperbolic sine as
sinh(x) = (pronounced as "sinch of x")
We define the hyperbolic cosine as
cosh(x) = (pronounced as "cosh of x")
ex – e-x
2
ex + e-x
2
Lastly, we have the hyperbolic trigonometric
functions. These functions are made from the
exponential functions with relations among
them that are similar to the trig-family.

79. Derivatives and Integrals of the Inverse
Trigonometric Functions
We define the hyperbolic sine as
sinh(x) = (pronounced as "sinch of x")
We define the hyperbolic cosine as
cosh(x) = (pronounced as "cosh of x")
ex – e-x
2
ex + e-x
2
We define the hyperbolic tangent, cotangent,
secant and cosecant as in the trig-family.
Lastly, we have the hyperbolic trigonometric
functions. These functions are made from the
exponential functions with relations among
them that are similar to the trig-family.

80. Derivatives and Integrals of the Inverse
Trigonometric Functions
The hyperbolic tangent:
tanh(x) =
sinh(x)
cosh(x) =
ex – e-x
ex + e-x
The hyperbolic cotangent:
coth(x) =
cosh(x)
sinh(x) =
ex – e-x
ex + e-x
The hyperbolic secant:
sech(x) =
1
cosh(x) =
ex + e-x
2
The hyperbolic cosecant:
csch(x) =
1
sinh(x) =
ex – e-x
2

81. Derivatives and Integrals of the Inverse
Trigonometric Functions
3,11,12,33,77,78,82,89,90.

82. As with the trig-family, we have the hyperbolic-
trig hexagram to help us with their relations.
Derivatives and Integrals of the Inverse
Trigonometric Functions

83. Hyperbolic Trig
Hexagram
Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
co-side
As with the trig-family, we have the hyperbolic-
trig hexagram to help us with their relations.

84. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Starting from any
position, take two
steps without
turning, we have
I =
II
III

85. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Starting from any
position, take two
steps without
turning, we have
I =
II
III
For example, staring at cosh(x), go to sinh(x)
then to tanh(x),

86. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Starting from any
position, take two
steps without
turning, we have
I =
II
III
For example, staring at cosh(x), go to sinh(x)
then to tanh(x), we get the relation
cosh(x) = sinh(x)
tanh(x)

87. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Starting from any
position, take two
steps without
turning, we have
I =
II
III
For example, staring at cosh(x), go to sinh(x)
then to tanh(x), we get the relation
cosh(x) = , similarly sech(x) =sinh(x)
tanh(x)
csch(x)
coth(x)

88. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:

89. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.

90. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.
The difference of
the squares on top
is the square of the
bottom one.

91. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.
The difference of
the squares on top
is the square of the
bottom one.
cosh2(x) – sinh2(x) = 1

92. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.
The difference of
the squares on top
is the square of the
bottom one.
cosh2(x) – sinh2(x) = 1
coth2(x) – 1 = csch2(x)

93. Derivatives and Integrals of the Inverse
Trigonometric Functions
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.
The difference of
the squares on top
is the square of the
bottom one.
cosh2(x) – sinh2(x) = 1
coth2(x) – 1 = csch2(x)
1 – tanh2(x) = sech2(x)

94. Derivatives and Integrals of the Inverse
Trigonometric Functions
Hyperbolic trig-functions show up in
engineering.

95. Derivatives and Integrals of the Inverse
Trigonometric Functions
Hyperbolic trig-functions show up in
engineering. Specifically the graph y = cosh(x)
gives the shape of a hanging cable.

96. Derivatives and Integrals of the Inverse
Trigonometric Functions
Graph of y = cosh(x)
Hyperbolic trig-functions show up in
engineering. Specifically the graph y = cosh(x)
gives the shape of a hanging cable.
(0, 1)

97. Derivatives and Integrals of the Inverse
Trigonometric Functions
The derivatives of the hyperbolic trig-functions
are similar, but not the same as, the trig-family.

98. Derivatives and Integrals of the Inverse
Trigonometric Functions
The derivatives of the hyperbolic trig-functions
are similar, but not the same as, the trig-family.
One may easily check that:
[sinh(x)]' = cosh(x)
[cosh(x)]' = sinh(x)

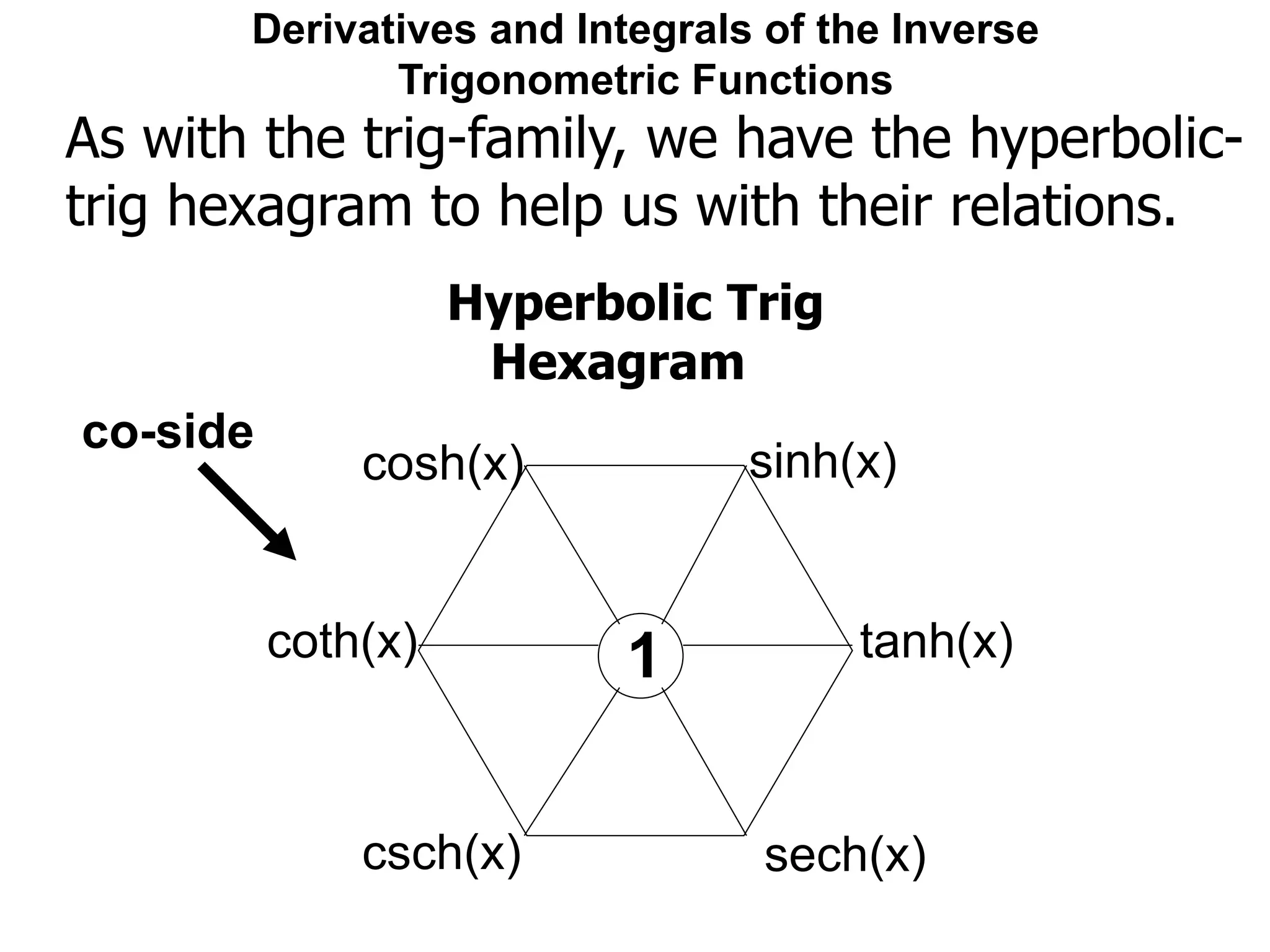
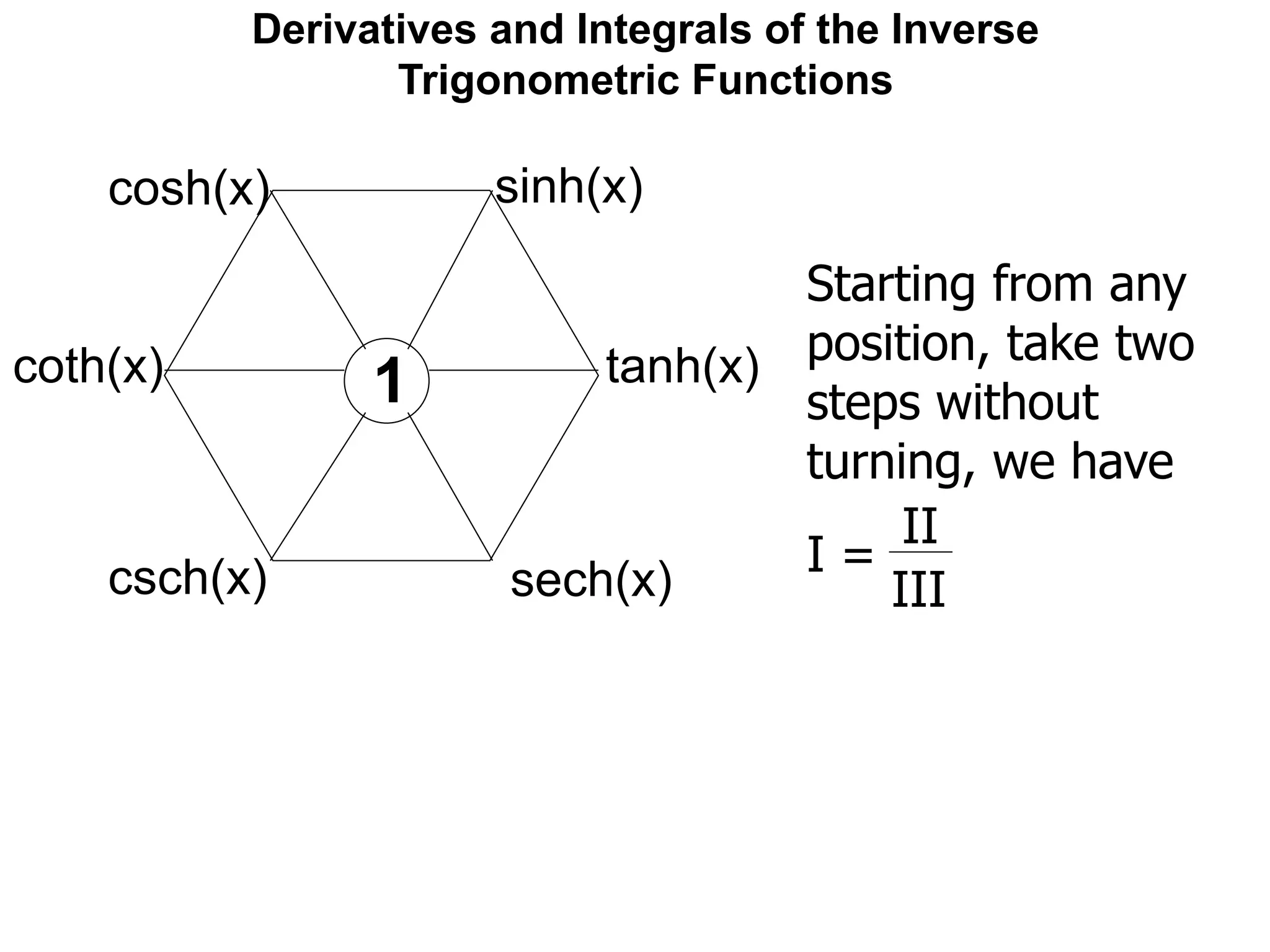
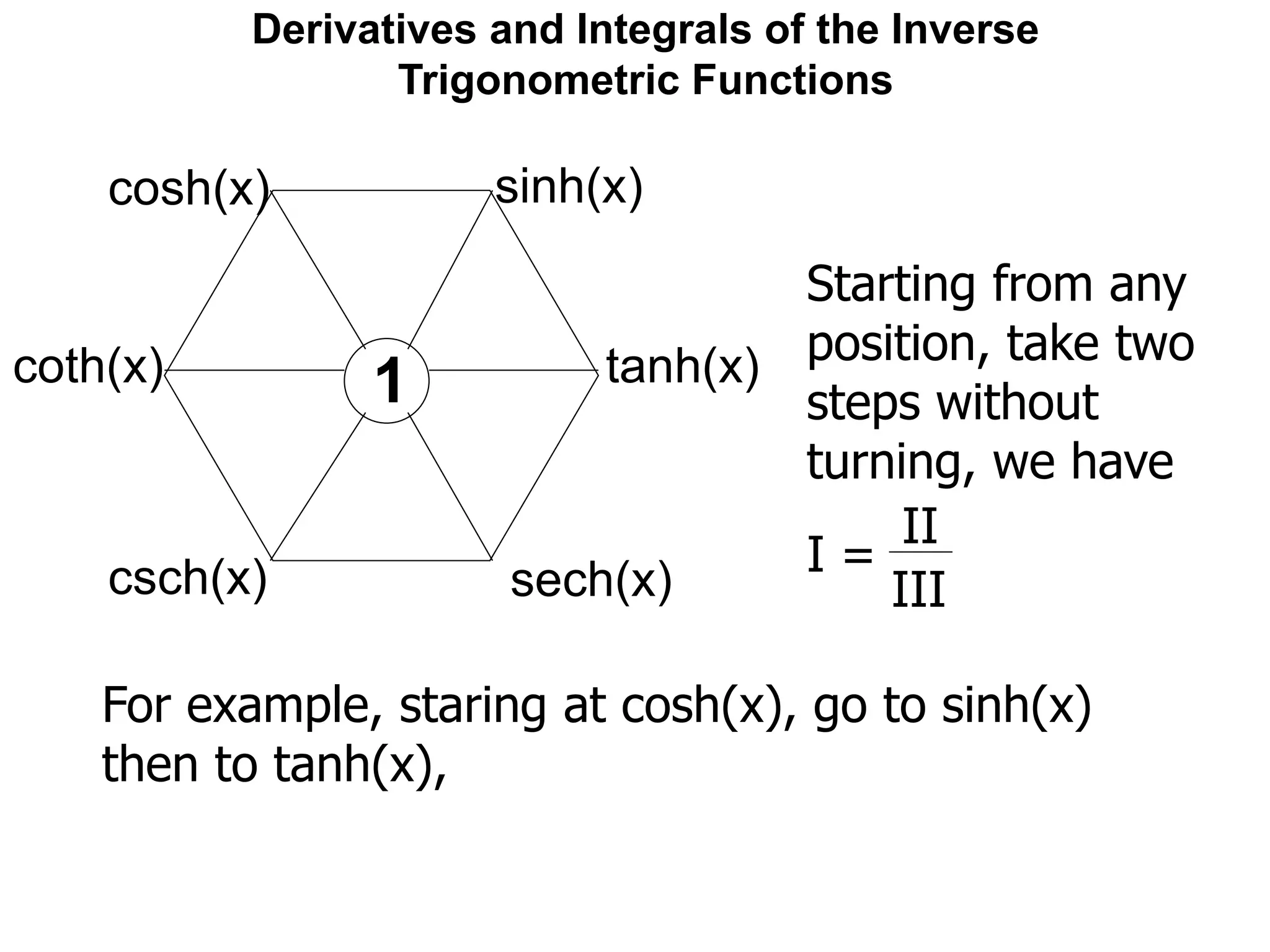
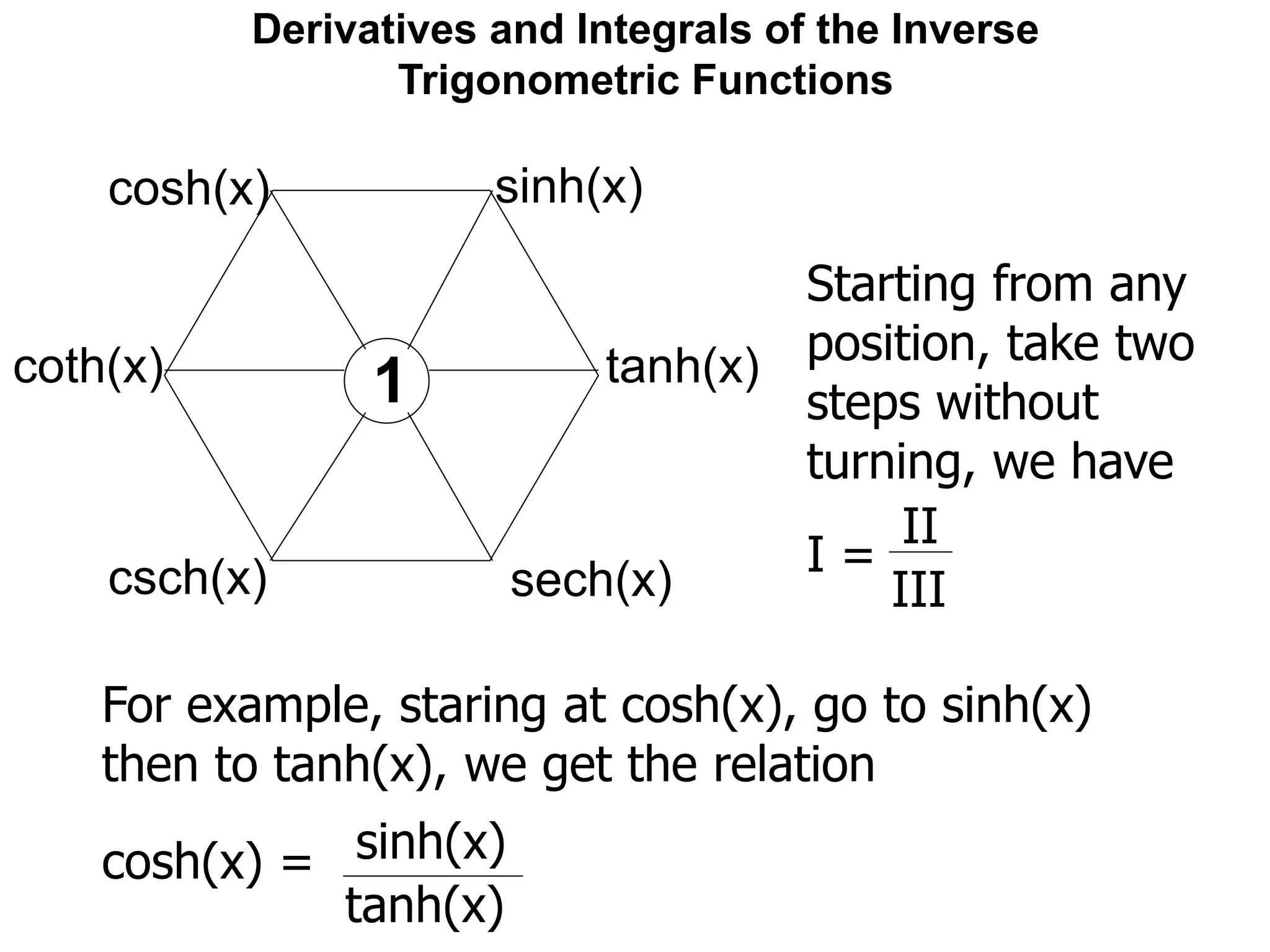
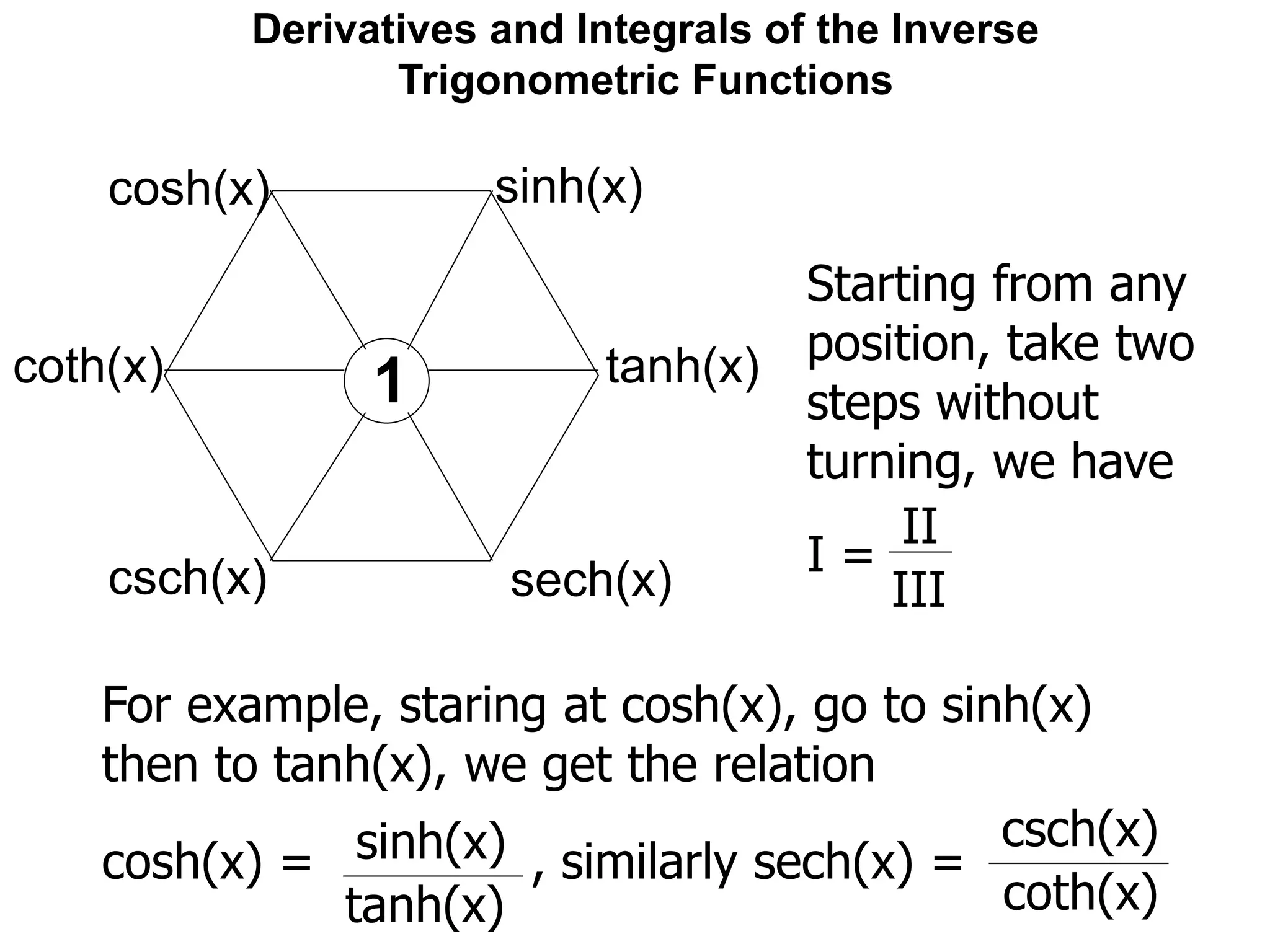
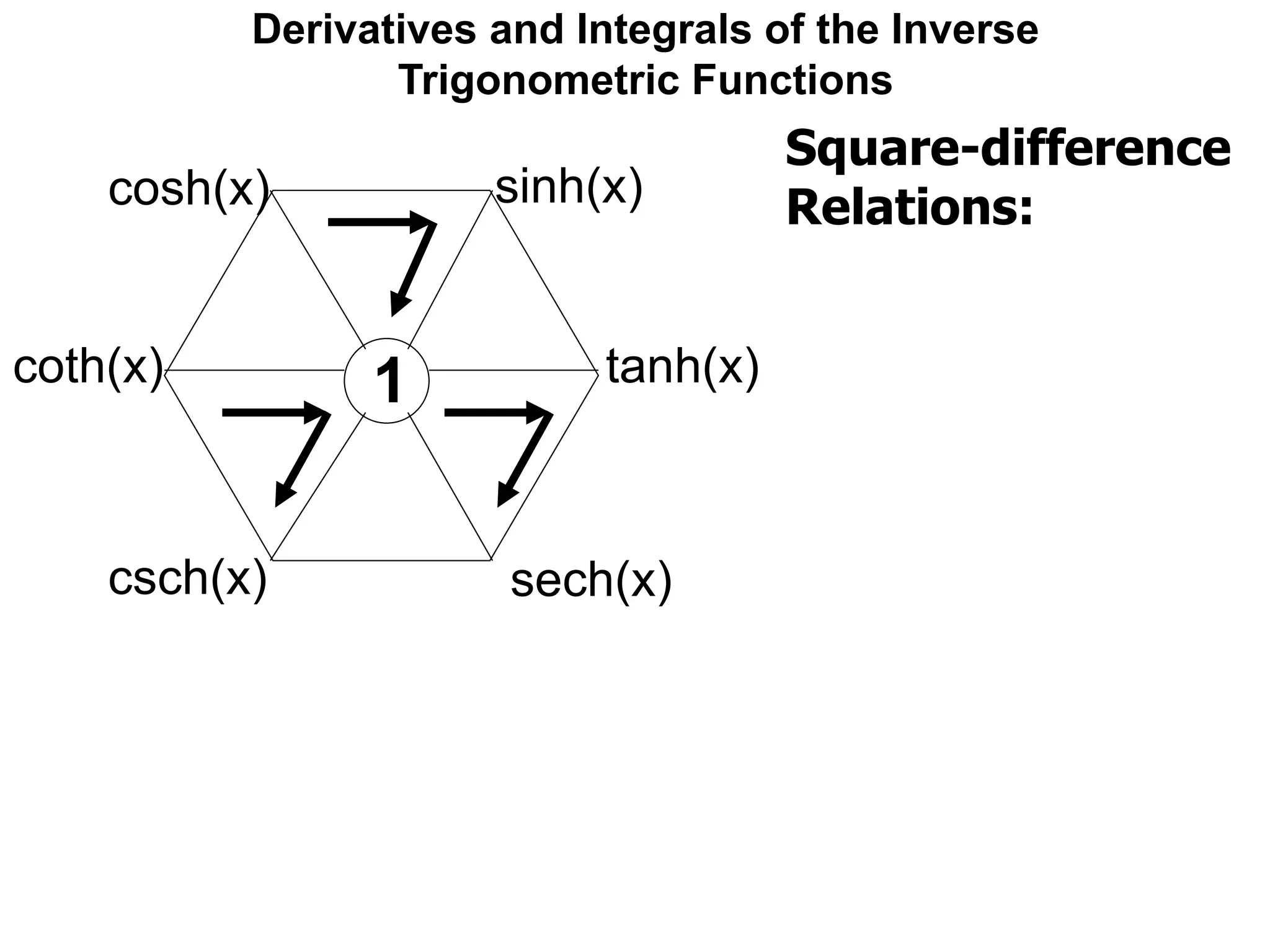
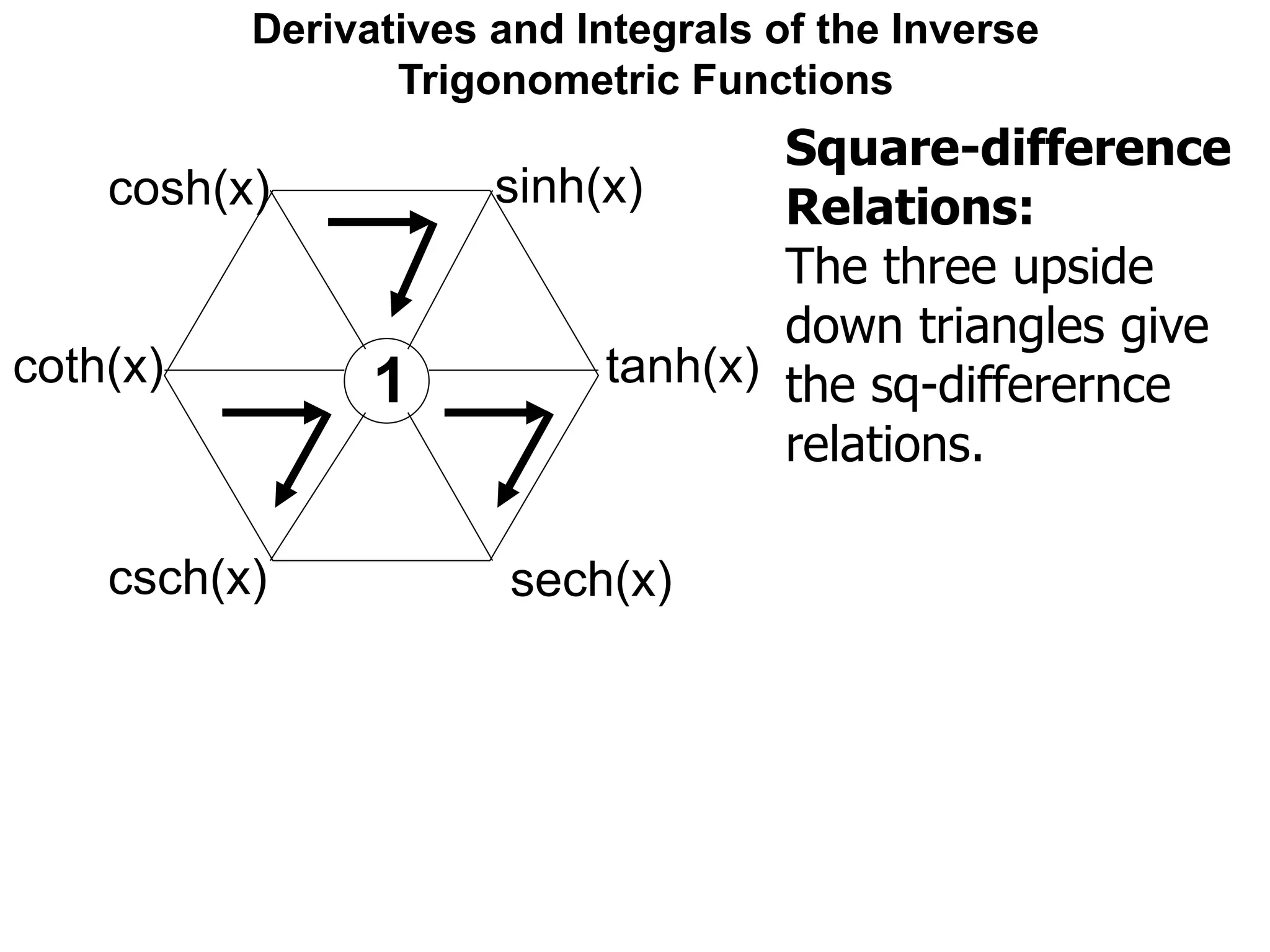
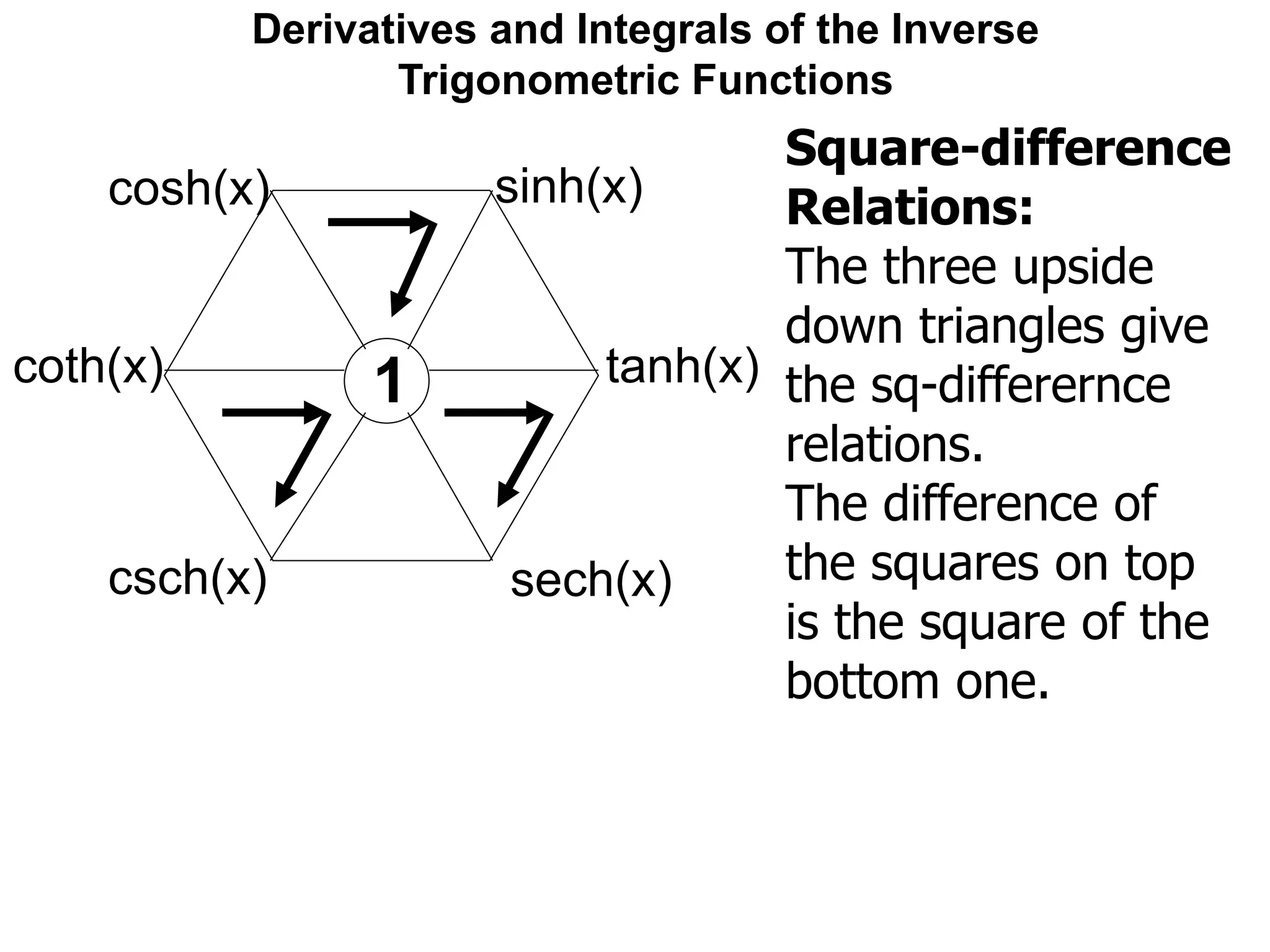
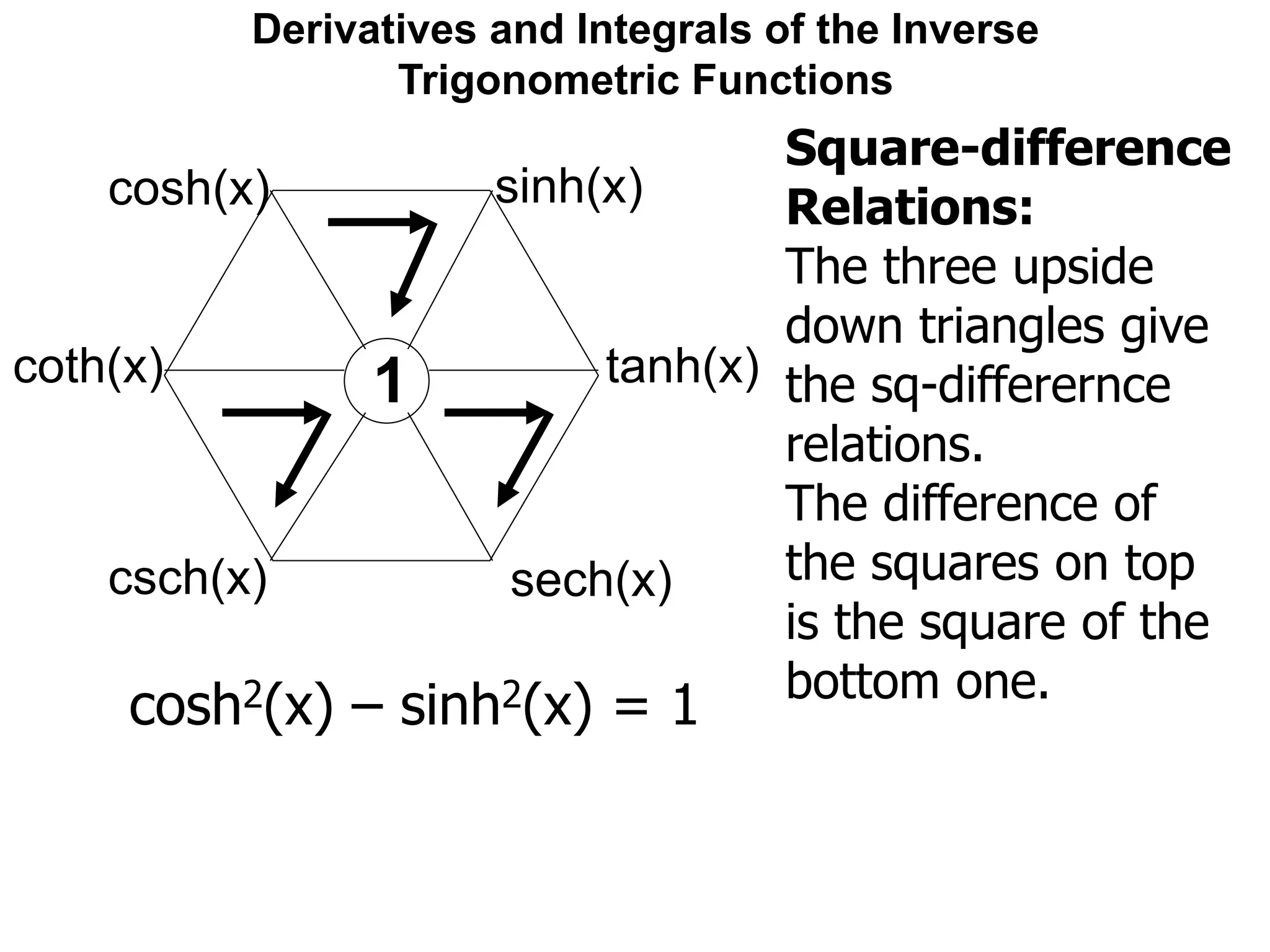
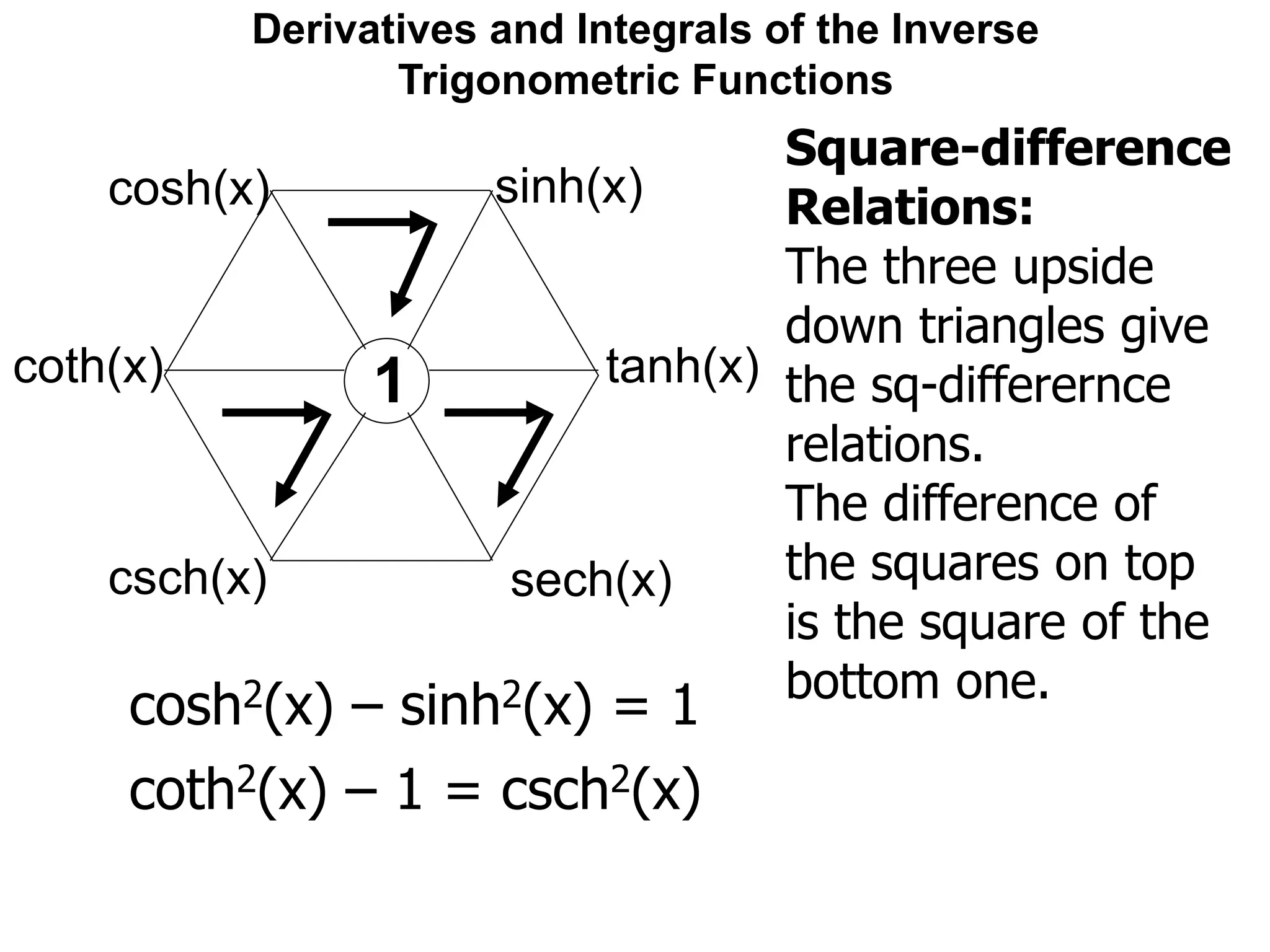
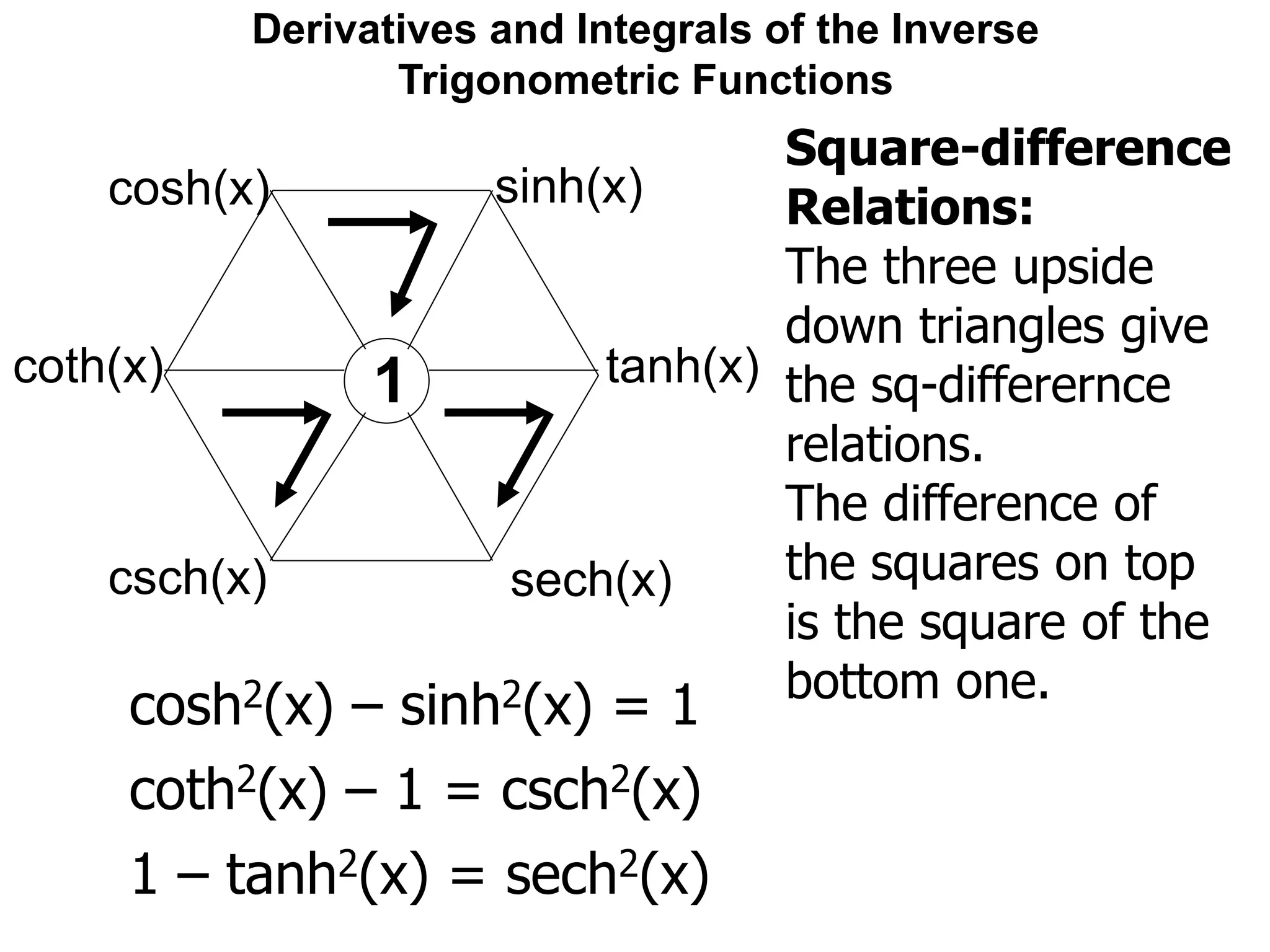
99. Derivatives and Integrals of the Inverse
Trigonometric Functions
The derivatives of the hyperbolic trig-functions
are similar, but not the same as, the trig-family.
One may easily check that:
[sinh(x)]' = cosh(x)
[cosh(x)]' = sinh(x)
[tanh(x)]' = sech2(x)
[coth(x)]' = -csch2(x)

100. Derivatives and Integrals of the Inverse
Trigonometric Functions
The derivatives of the hyperbolic trig-functions
are similar, but not the same as, the trig-family.
One may easily check that:
[sinh(x)]' = cosh(x)
[cosh(x)]' = sinh(x)
[tanh(x)]' = sech2(x)
[coth(x)]' = -csch2(x)
[sech(x)]' = -sech(x)tanh(x)
[csch(x)]' = -csch(x)coth(x)

F
r
a
n
k
M
a
2
0
0
6

101. Derivatives and Integrals of the Inverse
Trigonometric Functions
The derivatives of the hyperbolic trig-functions
are similar, but not the same as, the trig-family.
One may easily check that:
[sinh(x)]' = cosh(x)
[cosh(x)]' = sinh(x)
[tanh(x)]' = sech2(x)
[coth(x)]' = -csch2(x)
[sech(x)]' = -sech(x)tanh(x)
[csch(x)]' = -csch(x)coth(x)
HW. Write down the chain–rule versions of the
derivatives of the hyperbolic trig-functions.