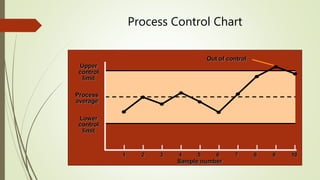
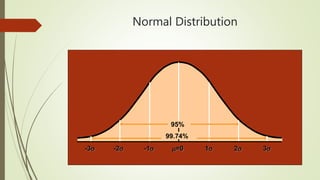
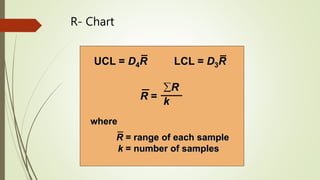
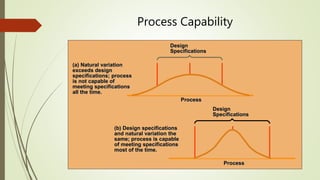
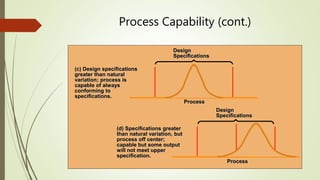
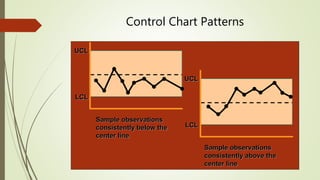
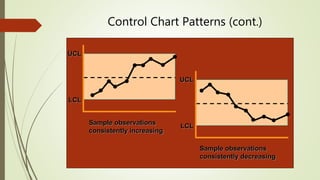
The document explains statistical process control (SPC) as a method for monitoring production processes to ensure quality through the use of control charts and understanding process capability. It highlights the historical development of SPC, its application in various industries, and the importance of continuous improvement in quality management. Additionally, the document details different types of control charts and their usage in identifying process variation and capability.

1. Statistical Process Control
The easiest and simple, but best explanation of Process Control. It will change your
whole concept about Process Control and take you to the new level of
understanding.

2. Presented By:
Muhammad Umar Saeed (14-MCT-22 )

3. Objectives
Basics of Statistical Process Control
Control Charts
Control Charts for Attributes
Control Charts for Variables
Control Chart Patterns
Process Capability

4. Introduction
 SPC was pioneered by Walter A. Shewhart in 1920s
 Control Charts developed in 1924
 The successful application in WWII
 The professional society in 1945

5. Basics of Statistical Process Control
 Statistical Process Control (SPC)
 monitoring production process to detect
and prevent poor quality
 Sample
 subset of items produced to use for
inspection
 Control Charts
 process is within statistical control limits
UCL
LCL

6. Variability
Random
Common causes
Inherent in a process
Can be eliminated only
through improvements
in the system
Non-Random
Special causes
Due to identifiable
factors
Can be modified through
operator or management
action

7. SPC in TQM
SPC
tool for identifying problems and make
improvements
contributes to the TQM goal of continuous
improvements

8. Quality Measures
 Attribute
a product characteristic that can be evaluated with a
discrete response
good – bad; yes - no
 Variable
a product characteristic that is continuous and can be
measured
weight - length

9. Applying SPC to Service
 Nature of defect is different in services
 Service defect is a failure to meet customer
requirements
 Monitor times, customer satisfaction

10. Applying SPC to Service (cont.)
 Hospitals
 timeliness and quickness of care, staff responses to requests, accuracy
of lab tests, cleanliness, courtesy, accuracy of paperwork, speed of
admittance and checkouts
 Grocery Stores
 waiting time to check out, frequency of out-of-stock items, quality of
food items, cleanliness, customer complaints, checkout register errors
 Airlines
 flight delays, lost luggage and luggage handling, waiting time at ticket
counters and check-in, agent and flight attendant courtesy, accurate
flight information, passenger cabin cleanliness and maintenance

11. Applying SPC to Service (cont.)
 Fast-Food Restaurants
 waiting time for service, customer complaints, cleanliness, food quality,
order accuracy, employee courtesy
 Catalogue-Order Companies
 order accuracy, operator knowledge and courtesy, packaging, delivery
time, phone order waiting time
 Insurance Companies
 billing accuracy, timeliness of claims processing, agent availability and
response time

12. Where to Use Control Charts
 Process has a tendency to go out of control
 Process is particularly harmful and costly if it goes out of
control
 Examples
 at the beginning of a process because it is a waste of time and money
to begin production process with bad supplies
 before a costly or irreversible point, after which product is difficult to
rework or correct
 before and after assembly or painting operations that might cover
defects
 before the outgoing final product or service is delivered

13. Control Charts
 A graph that establishes
control limits of a process
 Control limits
 upper and lower bands of a
control chart
 Types of charts
Attributes
p-chart
c-chart
Variables
range (R-chart)
mean (x bar – chart)

14. Process Control Chart
1 2 3 4 5 6 7 8 9 10
Sample number
Upper
control
limit
Process
average
Lower
control
limit
Out of control

15. Normal Distribution
=0 1 2 3-1-2-3
95%
99.74%

16. A Process Is in Control If …
1. … no sample points outside limits
2. … most points near process average
3. … about equal number of points above and below
centerline
4. … points appear randomly distributed

17. Control Charts for Attributes
p-charts
Uses portion defective in a sample
binomial distribution
c-charts
Uses number of defects in an item
Poisson distribution

18. p-Chart
UCL = p + zp
LCL = p - zp
z = number of standard deviations from
process average
p = sample proportion defective; an estimate
of process average
p = standard deviation of sample proportion
p =
p(1 - p)
n

19. c-Chart
UCL = c + zc
LCL = c - zc
where
c = number of defects per sample
c = c

20. Control Charts for Variables
Mean chart ( x -Chart )
uses average of a sample
Range chart ( R-Chart )
uses amount of dispersion in a sample

21. x-bar Chart
x =
x1 + x2 + ... xk
k
=
UCL = x + A2R LCL = x - A2R
= =
where
x = average of sample means=

22. R- Chart
UCL = D4R LCL = D3R
R =
R
k
where
R = range of each sample
k = number of samples

23. Using x- bar and R-Charts Together
Process average and process variability must be in
control.
It is possible for samples to have very narrow ranges,
but their averages is beyond control limits.
It is possible for sample averages to be in control, but
ranges might be very large.

24. Sample Size
Attribute charts require larger sample sizes
50 to 100 parts in a sample
Variable charts require smaller samples
2 to 10 parts in a sample

25. Process Capability
Tolerances
design specifications reflecting product
requirements
Process capability
range of natural variability in a process what we
measure with control charts

26. Process Capability
(b) Design specifications
and natural variation the
same; process is capable
of meeting specifications
most of the time.
Design
Specifications
Process
(a) Natural variation
exceeds design
specifications; process
is not capable of
meeting specifications
all the time.
Design
Specifications
Process

27. Process Capability (cont.)
(c) Design specifications
greater than natural
variation; process is
capable of always
conforming to
specifications.
Design
Specifications
Process
(d) Specifications greater
than natural variation, but
process off center;
capable but some output
will not meet upper
specification.
Design
Specifications
Process

28. Process Capability Measures
Process Capability Ratio
Cp =
=
tolerance range
process range
upper specification limit -
lower specification limit
6

29. Computing Cpk
Cpk = minimum
,
x - lower specification limit
3
=
upper specification limit - x
3
=
,

30. Control Chart Patterns
UCL
LCL
Sample observations
consistently above the
center line
LCL
UCL
Sample observations
consistently below the
center line

31. Control Chart Patterns (cont.)
LCL
UCL
Sample observations
consistently increasing
UCL
LCL
Sample observations
consistently decreasing

32. Example
 I want to sell coffee at 160c
 Modal A: 95.5%=0.955
Cp = 0.67 , Cpk =
 Modal B: 99.75%=0.9975 , 1/400 , (99.75) = 60.6%
Cp = 1.0 , Cpk =
 Modal C: 99.995%=0.999905 , 1/20,000 , (99.995) = 99.0%
Cp = 1.33 , Cpk = 1.067
 Modal D: 99.99995%= 0.9999995 , 1/2million , (99.99995) = 99.99%
Cp = 1.67 , Cpk =
 Modal E: 99.9999998%= 0.999999998, 1/500million , (99.9999998) = 99.99996%
Cp = 2.0 , Cpk =
200
200
200
200

33. Any Question?
I love to hear your question, as one said:
“He who is afraid to ask a question is ashamed
of learning”
“He who does not ask Remain a Fool Forever”