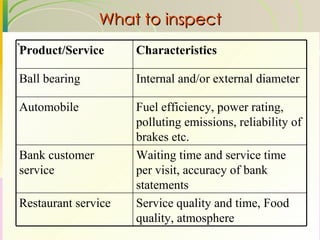
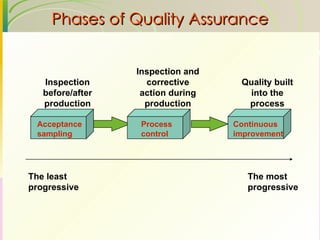
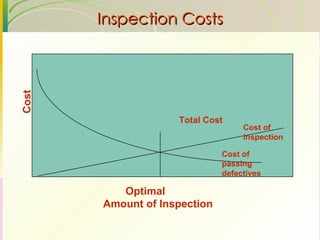
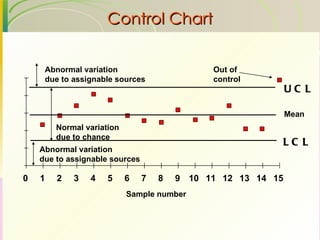
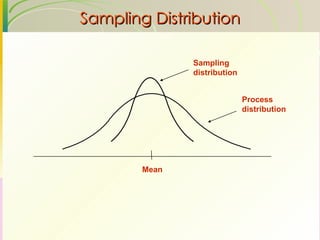
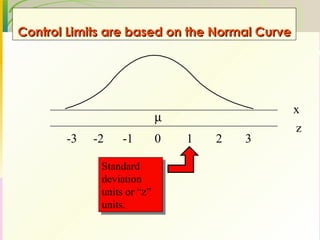
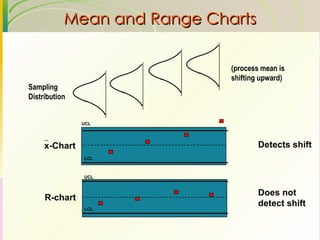
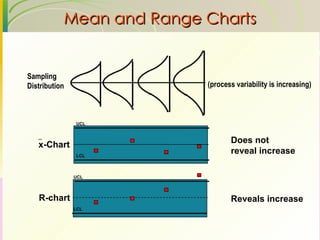
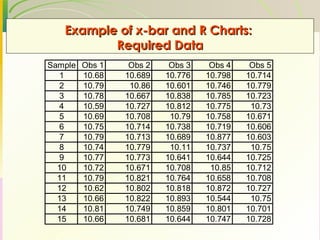
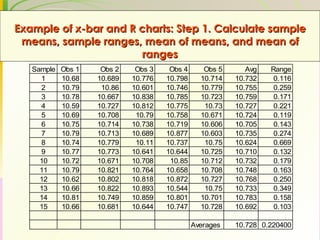
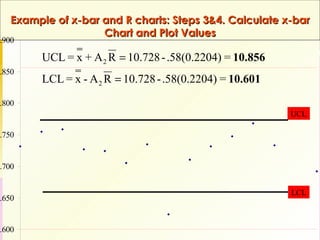
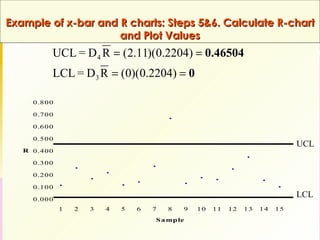
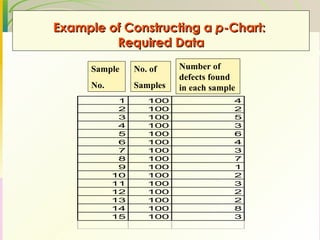
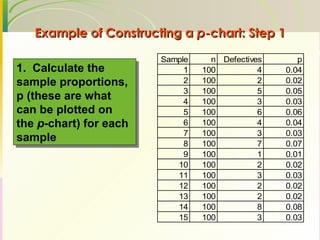
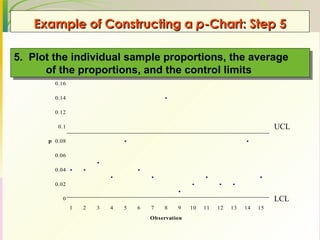
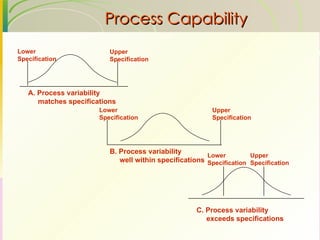
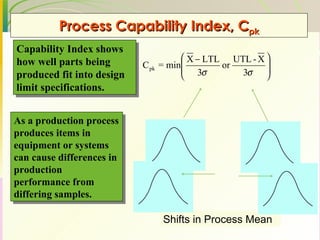
This document discusses quality assurance and statistical process control. It defines quality as meeting or exceeding customer expectations. It outlines three dimensions of quality: design quality, conformance quality, and performance quality. It also discusses objectives of quality assurance such as minimizing costs from inspection errors. Key aspects of statistical process control covered include control charts, process capability, sources of variation, and calculating control limits.

1. Quality Assurance (Statistical Process Control) By Dr. Debadyuti Das

2. Overview of Quality What does the term quality mean? Quality is the ability of a product or service to consistently meet or exceed customer expectations. Fitness for use (Juran) Conformance to requirements (Crosby)

3. Three Broad dimensions of Quality Design quality: Quality inherent in product design. Examples, Leather vs Vinyl seats for a car, Wider choice on the menu for an airline’s first-class passengers, Superior workmanship for increased precision, Tighter Engg. Specifications etc.

4. Three Broad dimensions of Quality Conformance Quality: Degree to which the product or service design specifications are met. Performance Quality: Product’s reliability and the ease of maintenance and repair service when required.

5. Another Dimensions of Quality Performance - main characteristics of the product/service Aesthetics - appearance, feel, smell, taste Special Features - extra characteristics Conformance - how well product/service conforms to customer’s expectations

6. Dimensions of Quality (Cont’d) Durability - useful life of the product/service Perceived Quality - indirect evaluation of quality (e.g. reputation) Serviceability – how difficult and expensive it is to repair Reliability - consistency of performance

7. Quality Assurance vs. Quality Management Quality Assurance Emphasis on finding and correcting defects before reaching market Quality Management Proactive, focusing on preventing mistakes from occurring Greater emphasis on customer satisfaction

8. Objectives of Quality Assurance To ensure the desired level of quality while minimizing the total expected cost resulting from sampling errors. In other words, To minimize the sum of costs related to Unnecessary process inspections (Type I error) Passing on defective items (Type II error)

9. QA system decision variables What to inspect How to inspect When to inspect Where to inspect

10. What to inspect ` Service quality and time, Food quality, atmosphere Restaurant service Waiting time and service time per visit, accuracy of bank statements Bank customer service Fuel efficiency, power rating, polluting emissions, reliability of brakes etc. Automobile Internal and/or external diameter Ball bearing Characteristics Product/Service

11. How to inspect Involves (1) the type of measurement (variables versus attributes) and (2) the method of measurement (choice of an appropriate man-machine system) Attributes Variables Carton Content of a certain ingredient in a drug Electric bulb Diameter of steel rod Transistor Hardness of steel Employee Mileage of a car Thermostat Waiting time in ATM, reservation centre

12. When to inspect Acceptance Sampling VS Process Control Process control is not feasible Process can be adjusted, stopped, inspected and started up again at a reasonable cost May be destructive or detrimental to the items Inspection not destructive or detrimental to the items Not very serious Consequences of passing on defectives are very high High Inspection cost per unit is low Acceptance Sampling Process Control

13. Phases of Quality Assurance Inspection before/after production Inspection and corrective action during production Quality built into the process The least progressive The most progressive Acceptance sampling Process control Continuous improvement

14. Where to inspect At customers’ arrival point, In special laboratories, At suppliers’ site In a Flow-shop layout, inspection stations are positioned along the production line. In a Job-shop, Inspection points are not fixed. In a Fixed position layout on large projects, inspection equipment and personnel are brought to the location of the product or service, e.g. Construction of tanker, bridge, surgical operation, staging a play etc.

15. Inspection Costs Cost of inspection Cost of passing defectives Total Cost Cost Optimal Amount of Inspection

16. Basic Forms of Variation Assignable variation is caused by factors that can be clearly identified and possibly managed Common variation (or Random variation) is inherent in the production process Example: A poorly trained employee that creates variation in finished product output. Example: A molding process that always leaves “burrs” or flaws on a molded item.

17. Statistical Process Control The essence of statistical process control is to assure that the output of a process is random so that future output will be random. The Control Process Define Measure Compare Evaluate Correct Monitor results

18. Control Chart Control Chart Purpose: to monitor process output to see if it is random A time ordered plot of sample statistics obtained from an ongoing process (e.g. sample means) Upper and lower control limits define the range of acceptable variation

19. Control Chart 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 UCL LCL Sample number Mean Out of control Normal variation due to chance Abnormal variation due to assignable sources Abnormal variation due to assignable sources

20. Sampling Distribution Sampling distribution Process distribution Mean

21. Control Limits are based on the Normal Curve x 0 1 2 3 -3 -2 -1 z  Standard deviation units or “z” units.

22. Control Limits We establish the Upper Control Limits (UCL) and the Lower Control Limits (LCL) with plus or minus 3 standard deviations from some x-bar or mean value. Based on this we can expect 99.73% of our sample observations to fall within these limits. LCL UCL 99.73% x

23. SPC Errors Type I error Concluding a process is not in control when it actually is. Type II error Concluding a process is in control when it is not.

24. Control Charts for Variables Mean control charts Used to monitor the central tendency of a process. X bar charts Range control charts Used to monitor the process dispersion R charts Variables generate data that are measured .

25. Mean and Range Charts UCL LCL UCL LCL R-chart Detects shift Does not detect shift (process mean is shifting upward) Sampling Distribution x-Chart

26. Mean and Range Charts UCL Does not reveal increase UCL LCL LCL R-chart Reveals increase (process variability is increasing) Sampling Distribution x-Chart

27. Control Chart for Attributes p-Chart - Control chart used to monitor the proportion of defectives in a process c-Chart - Control chart used to monitor the number of defects per unit Attributes generate data that are counted .

28. Use of p-Charts When observations can be placed into two categories. Good or bad Pass or fail Operate or don’t operate

29. Use of c-Charts Used only when the number of occurrences per unit of measure can be counted; non-occurrences cannot be counted. Scratches, chips, dents, or errors per item Cracks or faults per unit of distance Breaks or Tears per unit of area Bacteria or pollutants per unit of volume Calls, complaints, failures per unit of time

30. Example of x-bar and R Charts: Required Data

31. Example of x-bar and R charts: Step 1. Calculate sample means, sample ranges, mean of means, and mean of ranges

32. Example of x-bar and R charts: Step 2. Determine Control Limit Formulas and Necessary Tabled Values

33. Example of x-bar and R charts: Steps 3&4. Calculate x-bar Chart and Plot Values UCL LCL

34. Example of x-bar and R charts: Steps 5&6. Calculate R-chart and Plot Values UCL LCL

35. Example of Constructing a p -Chart: Required Data Sample No. No. of Samples Number of defects found in each sample

36. Statistical Process Control Formulas: Attribute Measurements ( p -Chart) Given: Compute control limits:

37. Example of Constructing a p -chart: Step 1 1. Calculate the sample proportions, p (these are what can be plotted on the p -chart) for each sample

38. Example of Constructing a p -chart: Steps 2 & 3 2. Calculate the average of the sample proportions 3. Calculate the standard deviation of the sample proportion

39. Example of Constructing a p -chart: Step 4 4. Calculate the control limits UCL = 0.0924 LCL = -0.0204 (or 0)

40. Example of Constructing a p -Chart: Step 5 5. Plot the individual sample proportions, the average of the proportions, and the control limits UCL LCL

41. Tolerances or specifications (Specification limit) Range of acceptable values established by engineering design or customer requirements Process variability (Process limit) Natural variability in a process Process capability Process variability relative to specification Process Capability

42. Process Capability C. Process variability exceeds specifications Lower Specification Upper Specification A. Process variability matches specifications Lower Specification Upper Specification B. Process variability well within specifications Lower Specification Upper Specification

43. Process Capability Ratio Process capability ratio, Cp = specification width process width Upper specification – lower specification 6  Cp =

44. Process Capability Index, C pk Shifts in Process Mean Capability Index shows how well parts being produced fit into design limit specifications. As a production process produces items in equipment or systems can cause differences in production performance from differing samples.