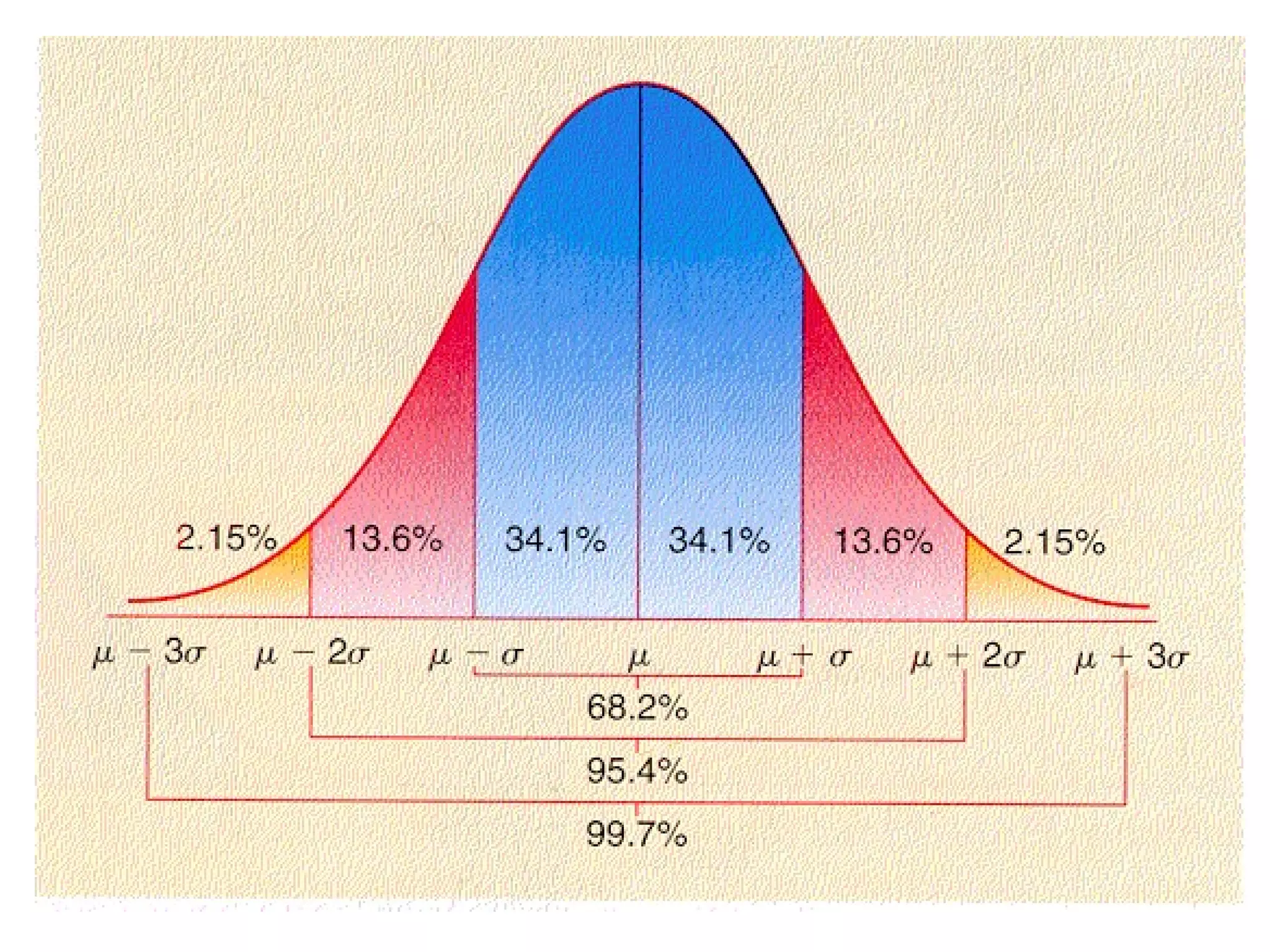
1. The document provides an overview of statistical analysis including the scientific method, common statistical terminology, hypotheses testing, choosing an appropriate statistical method, the normal distribution, and significance and confidence limits. 2. It explains key concepts like the null hypothesis, which is the opposite of the research hypothesis and is disproven through statistical testing. 3. Statistical methods depend on factors like the type of test needed, sample size, and data type, and whether tests of association, difference, or other analyses are required.

1. Statistical Analysis A Quick Overview

2. The Scientific Method Establishing a hypothesis (idea) Collecting evidence (often in the form of numerical data) Analysing the evidence (using statistical and other techniques) Accepting / rejecting the hypothesis, coming to conclusions and providing explanation Evaluating the process and making recommendation for the future

3. Basic Stuff ‘ X-bar’ is the mean ‘ n’ is the number in the sample (sample size) ‘ ∑ x’ is the “sum of”, in this case x (in other words add up all the individuals in the sample)

4. The Null Hypothesis The opposite of a hypothesis (in other words that there is no relationship between variables) Thus, rather than prove the hypothesis we disprove the null hypothesis If we cannot accept our null hypothesis then it is rejected and an alternative hypothesis can be accepted

5. Choosing a Method The statistical method chosen will largely depend on what type of test you need e.g. a test of association, a test of difference, probability testing, diversity, degree of clustering etc. Other factors such as sample size, data type (categorical vs. ordinal) and distribution are also important

6. Normal Distribution If a set of continuous variables is plotted against frequency the result is likely to be a belled shaped curve called the ‘normal’ curve The curve suggests that most individuals are aggregated around the average or mean (which in theory should be the middle of the curve) Thus, 68.2 % lie within 1 standard deviation, either side of the mean, 95.4% are clustered within 2 standard deviations etc. (the standard deviation is calculated using a formula and gives an indication of the reliability of the mean)

8. Significance and Confidence Limits Significance concerns the reliability of the data and is expressed as a percentage value The 95% level of significance is usually appropriate for field data This means that only 5 times out of 100 would this data (results) occur by chance In significance tables the 95% and 99% levels are indicated by 0.05 and 0.01 (i.e. 5% and 1% likelihood of the data occurring by chance) If the calculated value exceeds the theoretical (critical) value then the value is significant Thus we can say that we are confident, at the 95% or 99% level, of the reliability of the data

9. So where do we go from here? Take the data Check for normal distribution by plotting a frequency graph. 2. Take each hypotheses in turn There is a positive correlation between Place Utility and happiness (Subjective appreciation of life ). There is a significant difference between the happiness (subjective appreciation of life) of residents in two contrasting areas of Bratislava. 3. Use the flow chart to determine the appropriate test 4. Scatter the graphs and crunch the numbers 5. Test for significance 6. Draw your conclusions about the relationships and associations