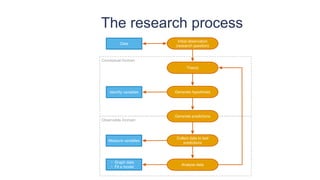
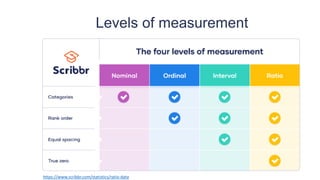
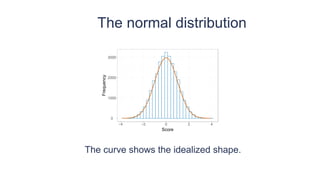
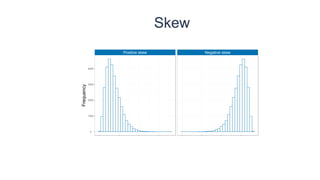
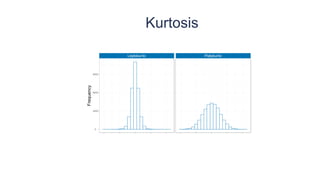
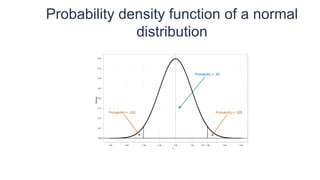
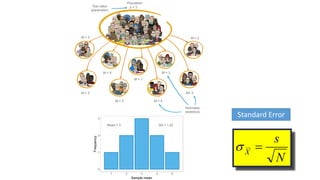
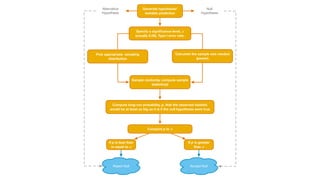
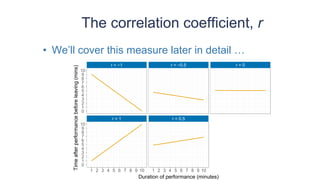
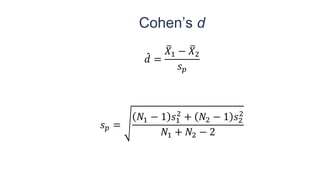
This document provides an overview of key concepts in statistical analysis and research methods. It discusses different types of data and variables, levels of measurement, validity and reliability, experimental and correlational research designs, measures of central tendency and dispersion, the normal distribution, hypothesis testing, and types of errors. It also covers effect sizes, correlations, and misconceptions about p-values and statistical significance. The document is serving as a learning module to help prepare students for quantitative methods and research.

1. Learning Module 1
Course Preparation:
Basic Statistical Concepts

2. Types of data analysis
• Quantitative Methods
– Testing theories using numbers
• Qualitative Methods
– Testing theories using language
• Magazine articles/Interviews
• Conversations
• Newspapers
• Media broadcasts

3. The research process

4. Test your theory
• Hypothesis:
– Coca-cola kills sperm.
• Independent Variable
– The proposed cause
– A predictor variable
– A manipulated variable (in experiments)
– Coca-cola in the hypothesis above
• Dependent Variable
– The proposed effect
– An outcome variable
– Measured not manipulated (in experiments)
– Sperm in the hypothesis above

5. Levels of measurement
• Categorical (entities are divided into distinct categories):
– Binary variable: There are only two categories
• e.g. dead or alive.
– Nominal variable: There are more than two categories
• e.g. whether someone is an omnivore, vegetarian, vegan, or fruitarian.
– Ordinal variable: The same as a nominal variable but the categories have a
logical order
• e.g. whether people got a fail, a pass, a merit or a distinction in their exam.
• Continuous (entities get a distinct score):
– Interval variable: Equal intervals on the variable represent equal differences in
the property being measured
• e.g. the difference between 6 and 8 is equivalent to the difference between 13 and 15.
– Ratio variable: The same as an interval variable, but the ratios of scores on the
scale must also make sense
• e.g. a score of 16 on an anxiety scale means that the person is, in reality, twice as anxious
as someone scoring 8.
https://www.scribbr.com/statistics/ratio-data

6. Validity
• Whether an instrument measures what it set out to
measure.
• Content validity
– Evidence that the content of a test corresponds to the
content of the construct it was designed to cover
• Ecological validity
– Evidence that the results of a study, experiment or test
can be applied, and allow inferences, to real-world
conditions.

7. Reliability
• Reliability
– The ability of the measure to produce the same results
under the same conditions.
• Test-Retest Reliability
– The ability of a measure to produce consistent results
when the same entities are tested at two different points
in time.

8. How to measure
• Correlational research:
– Observing what naturally goes on in the world without
directly interfering with it.
• Experimental research:
– One or more variable is systematically manipulated to
see their effect (alone or in combination) on an outcome
variable.
– Statements can be made about cause and effect.

9. Types of variation
• Systematic Variation
– Differences in performance created by a specific
experimental manipulation.
• Unsystematic Variation
– Differences in performance created by unknown factors.
• Age, Gender, IQ, Time of day, Measurement error etc.
• Randomization
– Minimizes unsystematic variation.

10. Analysing data: histograms
• Frequency Distributions (aka Histograms)
– A graph plotting values of observations on the horizontal
axis, with a bar showing how many times each value
occurred in the data set.
• The ‘Normal’ Distribution
– Bell shaped
– Symmetrical around the centre

11. The normal distribution
The curve shows the idealized shape.
0
1000
2000
3000
−4 −2 0 2 4
Score
Frequency

12. Properties of frequency distributions
• Skew
– The symmetry of the distribution.
– Positive skew (scores bunched at low values with the tail
pointing to high values).
– Negative skew (scores bunched at high values with the tail
pointing to low values).
• Kurtosis
– The ‘heaviness’ of the tails.
– Leptokurtic = heavy tails.
– Platykurtic = light tails.

13. Skew
Positive skew Negative skew
0
1000
2000
3000
4000
Frequency

14. Kurtosis
Leptokurtic Platykurtic
0
3000
6000
9000
Frequency

15. Central tendency: the mode
• Mode
– The most frequent score
• Bimodal
– Having two modes
• Multimodal
– Having several modes

16. Central tendency: the median
• The Median is the middle score when scores are
ordered:

17. Central tendency: the mean
• Mean
– The sum of scores divided by the number
of scores.
– Number of friends of 11 Facebook users.

18. The dispersion: range
• The Range
– The smallest score subtracted from the largest
– For our Facebook friends data the highest score is 234
and the lowest is 22; therefore the range is: 234 −22 =
212

19. The dispersion: the interquartile range
• Quartiles
– The three values that split the sorted data into four
equal parts.
– Second Quartile = median.
– Lower quartile = median of lower half of the data
– Upper quartile = median of upper half of the data

20. Sum of squared errors, SS
• Indicates the total dispersion, or total deviance of scores
from the mean:
• More useful to work with the average dispersion, known as
the variance:

21. Standard deviation
• The variance gives us a measure in units squared.
– In our Facebook example we would have to say
that the average error in out data was 3224.6
friends squared.
• This problem is solved by taking the square root of
the variance, which is known as the standard
deviation:

22. Important things to remember
• The sum of squares, variance, and standard
deviation represent the same thing:
– The ‘Fit’ of the mean to the data
– The variability in the data
– How well the mean represents the observed data
– Error

23. Going beyond the data: z-scores
• Z-scores
– Standardising a score with respect to the other
scores in the group.
– Expresses a score in terms of how many
standard deviations it is away from the mean.
– The distribution of z-scores has a mean of 0
and SD = 1.
s
X
X
z
−
=

24. Probability density function of a normal
distribution
z
Density
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
−4.00 −3.00 −1.96 −1.00 0.00 1.00 1.65 1.96 3.00 4.00
Probability = .025 Probability = .025
Probability = .95

25. Populations and samples
• Population
– The collection of units (be they people, plankton, plants,
cities, suicidal authors, etc.) to which we want to
generalize a set of findings or a statistical model.
• Sample
– A smaller (but hopefully representative) collection of units
from a population used to determine truths about that
population

26. Samples and populations
• Sample
– Mean and Standard Deviation(SD) describe only the sample from
which they were calculated.
• Population
– Mean and SD are intended to describe the entire population (very
rare in Psychology).
• Sample to population:
– Mean and SD are obtained from a sample, but are used to estimate
the mean and SD of the population (very common in psychology).

27. N
s
X
=

0
1
2
3
1 2 3 4 5
Sample mean
Frequency
Population
µ = 3
M = 3
Mean = 3 SD = 1.22
True value
(parameter)
Estimates
(statistics)
M = 3
M = 3
M = 4
M = 4
M = 2
M = 2
M= 5
M = 1
Standard Error

28. Types of hypotheses
• Null hypothesis, H0
• There is no effect.
• E.g. Big Brother contestants and members of the public will not differ in
their scores on personality disorder questionnaires
• The alternative hypothesis, H1
• AKA the experimental hypothesis
• E.g. Big Brother contestants will score higher on personality disorder
questionnaires than members of the public

30. Type I and Type II errors
• Type I error
– Occurs when we believe that there is a genuine effect in
our population, when in fact there isn’t.
– The probability is the α-level (usually 0.05)
• Type II error
– Occurs when we believe that there is no effect in the
population when, in reality, there is.
– The probability is the β-level (often 0.2)

31. Misconceptions around p-values
• Misconception 1: A significant result means that the
effect is important
– No, because significance depends on sample size.
• Misconception 2: A non-significant result means that the
null hypothesis is true
– No, a non-significant result tells us only that the effect is not
big enough to be found (given our sample size), it doesn’t tell
us that the effect size is zero.
• Misconception 3: A significant result means that the null
hypothesis is false?
– No, it is logically not possible to conclude this .

32. Effect sizes
• An effect size is a standardized measure of the size
of an effect:
– Standardized = comparable across studies
– Not (as) reliant on the sample size
– Allows people to objectively evaluate the size of observed
effect.

33. Effect size measures
• There are several effect size measures that can be
used:
– Cohen’s d
– Pearson’s r

34. The correlation coefficient, r
• We’ll cover this measure later in detail …
r = −1 r = −0.5 r = 0
r = 1 r = 0.5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
Duration of performance (minutes)
Time
after
performance
before
leaving
(mins)

35. Cohen’s d
መ
𝑑 =
ത
𝑋1 − ത
𝑋2
𝑠𝑝
𝑠𝑝 =
𝑁1 − 1 𝑠1
2
+ 𝑁2 − 1 𝑠2
2
𝑁1 + 𝑁2 − 2

36. Effect size measures
• r = .1, d = .2 (small effect):
– the effect explains 1% of the total variance.
• r = .3, d = .5 (medium effect):
– the effect accounts for 9% of the total variance.
• r = .5, d = .8 (large effect):
– the effect accounts for 25% of the variance.