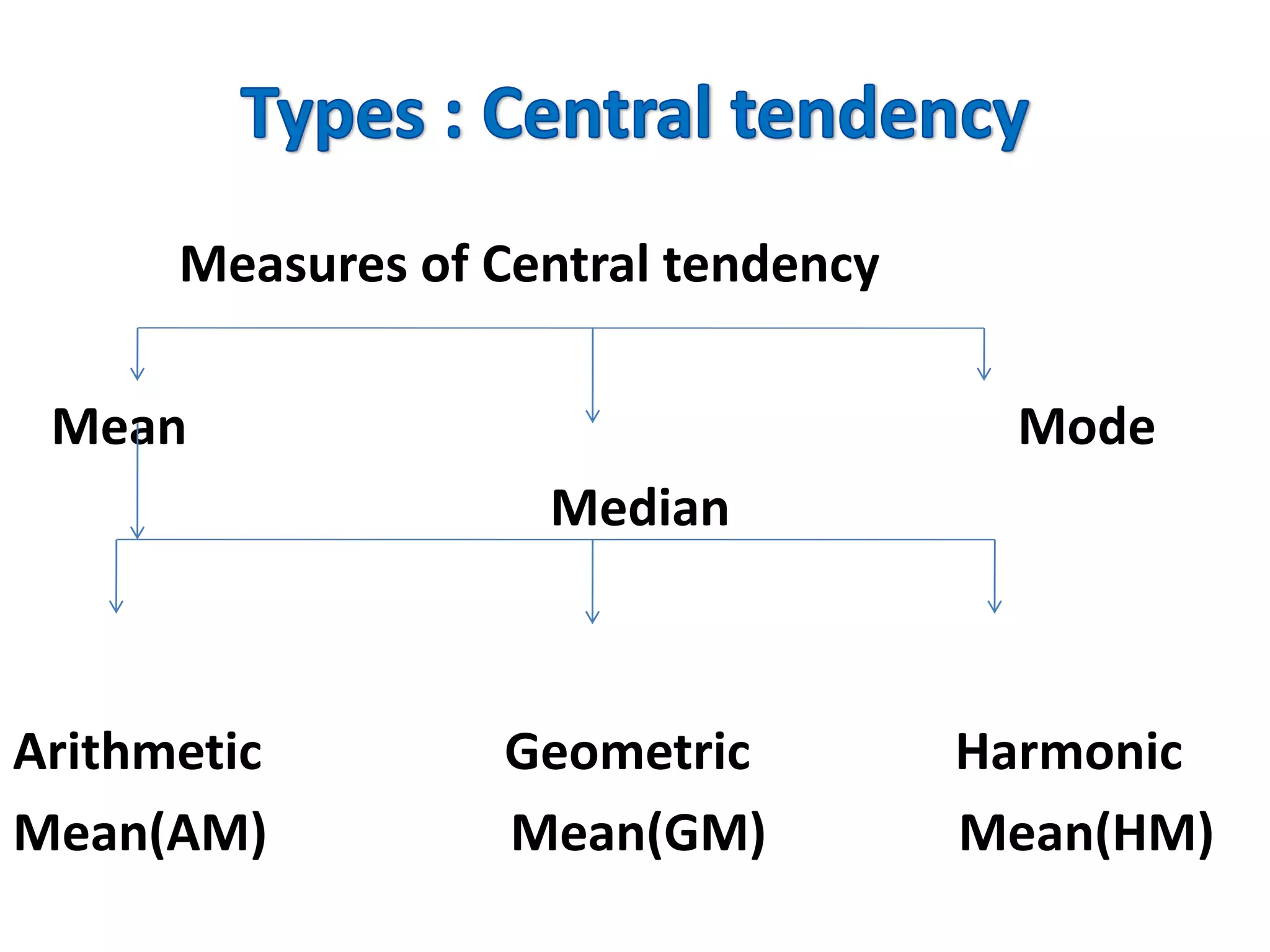
Statistical analysis and its applications can be used in many fields including pharmaceutical research, clinical trials, public health, epidemiology, genetics, and demographics. Some key uses of statistics include evaluating drug effects, comparing drug treatments, exploring associations between diseases and risk factors, and analyzing clinical trial and genomics data. Measures of central tendency, dispersion, and other statistical methodologies help researchers draw conclusions from collected data.

1. STATISTICAL ANALYSIS AND ITS APPLICATIONS

2. STATISTICS
It refers to the body of technique or methodology
which has been developed for the collection
,presentation and analysis of quantitative data
and for the use of such data in decision-making
OR
 The science of statistics is the method of judging
collection ,natural or social phenomenon from
the results obtained from the analysis or
enumeration or collection of estimates
Gupta,S.C., Kapoor,v.k., (2013) fundamentals of mathematical statistics. 11th Ed,Sultan Chand & Sons educational publishers

3. STATISTICAL METHODOLOGIES
1) Descriptive Statistics:-summarizes data from
a sample using indexes such as the mean or
standard deviation
2) Inferential Statistics:- Draws conclusion from
data that are subject to random variations e.g
observational errors,sampling variations

4.  When a series of observations have been tabulated in
the form of frequency distribution
 it is felt necessary to convert a series of observation in
a single value, that describes the characteristics of that
distribution,→ called Measure Of Central Tendency
 All data or values are clustered round it
 These values enable comparisons to be made between
one series of observations and another
 Individual values may overlap, two distributions have
different central tendency
 E.g., average incubation period of measles is 10 days
and that of chicken pox is 15 days.

5. Measures of Central tendency
Mean Mode
Median
Arithmetic Geometric Harmonic
Mean(AM) Mean(GM) Mean(HM)

6. Arithmetic mean:
Sum of all observations divided by number of
observations
Mean(x)=Sx/n; x is a variable taking different
observational values & n= no. of observations
Exmp.
ESR of 7 subjects are 8,7,9,10,7,7, & 6 mm for 1st hr.
Calculate mean ESR.
- Mean(x)= (8+7+9+10+7+7+6)/7=54/7=7.7 mm
PROPERTIES:
Uniqueness:- Given set of data one and only one
arithmetic mean
Simplicity:- easily understood and easy to compute

7. Median :
 when observations are arranged in ascending or
descending order of magnitude, the middle most value is
known as Median.
 Problem:
 From same example of ESR, observations are arranged first
in ascending order: 6,7,7,7,8,9,10.
 Median= {7+1}/2=8/2=4th observation I,e., 7
 When n is Odd no., Median={n+1}2 th observation
 When n is Even no., Median={n/2th + (n/2+1)th}/2 th
observation
 Problem: suppose, there are 8 observations of ESR like
5,6,7,7,7,8,9,10
 Median={8/2th +(8/2+1)th}/2={4th+5th obs}/2=(7+7)/2=7

8. Mode:
The observation, which occurs most frequently in
series
Problem: ESR of 7 subjects are 8,7,9,10,7,7, & 6 mm
for 1st hr. Calculate the Mode.
- Mode is 7.

9. Calculation of weighted arithmetic mean:
Following methods are utilized in case of large
no. of observations
For Ungrouped Data:
Suppose we have x₁, x₂, x₃,…nth observations
with corresponding frequencies f₁, f₂,f₃,…fn
Mean=
𝑥1
𝑓1
+𝑥2
𝑓2
+𝑥3
𝑓3
+⋯+𝑥𝑛𝑓𝑛
𝑓1
+𝑓2
+𝑓3
+⋯+𝑓𝑛
=
𝑓𝑥
𝑓
=
𝑓𝑥
𝑛

10. For grouped Date:
Data are arrange in groups & frequency
distribution table are prepared
Mean value of each group is multiplied by
frequency
Sum of product value is divided by total no of
observations
Mean such obtained is called “ weighted
mean”
Mean(x)=
𝑥1
𝑓1
+𝑥2
𝑓2
+𝑥3
𝑓3
+⋯+𝑥𝑛𝑓𝑛
𝑓1
+𝑓2
+𝑓3
+⋯+𝑓𝑛
=
𝑓𝑥
𝑓
=
𝑓𝑥
𝑛

11. Geometric mean:
 Used when data contain a few extremely large or small
values
 It’s the nth root product of n observastions
 GM=ⁿ√(x₁.x₂.x₃….xn)
Harmonic Mean:
 Reciprocal of the arithmetic mean of reciprocals of
observations
 arithmetic mean of reciprocals of observations=S(⅟x)
 HM=n/S⅟x
 got limited use
 A.M>GM>HM

12. • Measures of central tendency do not provide information
about spread or scatter values around them
• Measures of dispersion helps us to find how individual
observations are dispersed or scattered around the mean
of a large series of data
• Different measures of Dispersion are:
i. Range
ii. Mean deviation
iii. Standard deviation
iv. Variance
v. Coefficient of variation

13. Range:
- Difference between highest & lowest value
- Defines normal value of a biological characteristic
• Problem: Systolic blood pressure (mm of Hg) of 10 medical
students as follows: 140/70, 120/88, 160/90, 140/80,
110/70, 90/60, 124/64, 100/62, 110/70 & 154/90
• Range of Systolic BP of medical students = highest value-
lowest value=160-90=70mm of Hg
• Range of Diastolic BP= 90-60=30 mm of Hg

14. Mean deviation:
- Average deviations of observations from mean value
- Mean Deviation(S) =(x-x)/n,
where x=observation,
x=Mean
Gupta,s.c.,kapoor,v.k,. ( 2013 ) fundamentals of mathematical statistics .11th Ed,sultan chand & sons

15. Standard Deviation:
 Most frequently used measures of dispersion
 Square root of the arithmetic mean of the square of
deviations taken from the arithmetic mean.
 In simple term “ Root-Mean-Square-Deviation”
 𝑆𝐷(s)= √
𝑥−𝑥 2
𝑛
 Where x= observation
X=Mean
 n=no. of observations

16.  To estimate variability in population from values of a sample, degree
of freedom is u in placed of no. of observations
 Standard deviation is calculated by following stages:
 Calculate the mean
 Calculate the difference between each observation & mean
 Square the difference
 Sum the squared values
 Divide the sum of squares by the no. of observations(n) to get mean
square deviation or variances(s)
 Find the square root of variance to get “Root-Mean-Square-
Deviation”
 Use: sample size calculation of any study
 - Summarizes deviation of a large series of observation around mean
in a single value

17. Coefficient of Variation:
- Used to denote the comparability of variances of two or
more different sets of observations
- Coefficient of Variation=(sd/Mean) x 100
- Coefficient of Variation indicates relative variability

18. Statistics and its application
 Pharmaceutical statistics is the application of statistics to matters
concerning the pharmaceutical industry. This can be from issues of
design of experiments, to analysis of drug trials, to issues of
commercialization of a medicine.
 Evaluate the activity of a drug; e.g.; effect of caffeine on attention;
compare the analgesic effect of a plant extract and NSAID
 To explore whether the changes produced by the drug are due to
the action of drug or by chance
 To compare the action of two or more different drugs or different
dosages of the same drug are studied using statistical methods.
 To find an association between disease and risk factors such as
Coronary artery disease and smoking
Gupta,S.c.,Kapoor,v.k,.(2013) fundamentals of mathematical statistics . 11th Ed,sultan & chand sons

19. Statistics and its application cont….
 Public health, including epidemiology, health services research, nutrition,
environmental health and healthcare policy & management.
 Design and analysis of clinical trials in medicine
 Population genetics, and statistical genetics in order to link variation in
genotype with a variation in phenotype. In biomedical research, this work
can assist in finding candidates for gene alleles that can cause or influence
predisposition to disease in human genetics
 Analysis of genomics data. Example: from microarray or proteomics
experiments. Often concerning diseases or disease stages.
 Systems biology for gene network inference or pathways analysis
 Demographic studies: Age, gender, height, weight, BMI
 Epidemiology: deficiency of iron in anemia, iodized salt and goiter, hygiene
and microbial disease