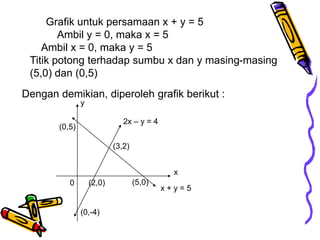
Dokumen tersebut membahas tentang Sistem Persamaan Linier Dua Variabel (SPLDV), yang terdiri atas dua persamaan linier dengan dua variabel. Ada beberapa metode untuk menyelesaikannya, yaitu metode grafik, substitusi, dan eliminasi. Metode grafik menggambar kedua persamaan dan mencari titik potongnya. Metode substitusi menyatakan satu variabel dalam variabel lain. Metode eliminasi menghapus satu variabel dengan mengurangi pers

1. Sistem Persamaan Linier Dua
Variabel (SPLV)

2. Tujuan Pembelajaran
Siswa dapat menyelesaikan sistem
persamaan linier dua variabel dengan
metode grafik, substitusi, dan eliminasi.

3. Sistem Persamaan Linier Dua Variabel terdiri atas
dua persamaan linier berbentuk :
a1x + b1y = c1 dan a2x + b2y = c2
dengan a, b, c ∈ R dan a ≠ 0, b ≠ 0, serta x dan y
merupakan variabel.
Nilai x dan y yang memenuhi kedua persamaan
tersebut merupakan penyelesaian sistem
persamaan linear dua variabel

4. Ada beberapa metode untuk menyelesaikan Sistem
Persamaan Linier Dua Variabel yaitu :
1. Metode Grafik
2. Metode Substitusi (Penggantian)
3. Metode Eliminasi (Pelenyapan)

5. 1. Metode Grafik
Penyelesaian sistem persamaan linear
dua variabel dengan cara menggambar
persamaan-persamaan tersebut dalam
satu diagram cartesius.
Dari gambar tesebut diperoleh titik
potong kedua garis yang merupakan
himpunan dari Penyelesaian sistem
persamaan linear dua variabel

6. Contoh :
Tentukan himpunan Penyelesaian dari sistem persamaan
∈
2x – y = 4 dan x + y = 5 untuk x,y R
Penyelesaian :
Grafik untuk persamaan 2x – y = 4
Ambil y = 0, maka x = 2
Ambil x = 0, maka y = -4
Titik potong terhadap sumbu x dan y masing-masing
(2,0) dan (0,-4)

7. Grafik untuk persamaan x + y = 5
Ambil y = 0, maka x = 5
Ambil x = 0, maka y = 5
Titik potong terhadap sumbu x dan y masing-masing
(5,0) dan (0,5)
Dengan demikian, diperoleh grafik berikut :
y
2x – y = 4
(0,5)
(3,2)
x
0 (2,0) (5,0)
x+y=5
(0,-4)

8. 2. Metode Substitusi (Penggantian)
Menyatakan variabel yang satu ke dalam
variabel lain pada suatu persamaan
Contoh :
Tentukan himpunan penyelesaian dari sistem
persamaan 2x – y = 4 dan x + y = 5 untuk x, y ∈ R
Penyelesaian :
2x – y = 4 ……………. ( Pers.1 )
x+y=5 ……………. ( Pers.2 )

9. Dari persamaan (1), 2x – y = 4 dapat diubah menjadi
y = 2x – 4.
Kemudian nilai y disubstitusikan pada persamaaan (2).
Sehingga diperoleh :
x + y = 5 ↔ x + 2x – 4 = 5
↔ 3x – 4 = 5
↔ 3x = 5 + 4
↔ 3x = 9
↔ x=3

10. Nilai y diperoleh dengan menyubstitusikan nilai x = 3
pada persamaan (1) atau (2)
sehingga diperoleh :
2x – y = 4 ↔ 2 x 3 – y = 4
↔ 6–y=4
↔ y=4–6
↔ y = -2
Jadi himpunan penyelesaian sistem persamaan linear
tersebut adalah {(3,2)}

11. 3. Metode Eliminasi ( Pelenyapan )
Mengeliminasi atau melenyapkan salah satu
variabel dan variabel yang akan dieliminasi
harus mempunyai koefisien yang sama.
Contoh :
Tentukan himpunan penyelesaian dari sistem
persamaan 2x + y = 8 dan x - y = 10 untuk x, y∈ R

12. 2x + y = 8
x - y = 10 +
3x = 18
x=6
2x + y = 8 | x 1 | 2x + y = 8
x - y = 10 | x 2 | 2x – 2y = 20 -
3y = -12
y = -4
Jadi, himpunan penyelesaiannya adalah {(6,-4)}

13. Wassalamu’alaikum