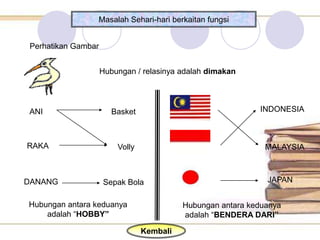
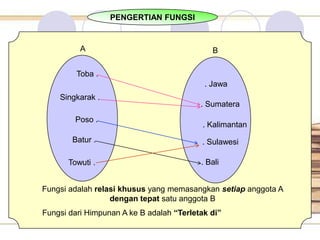
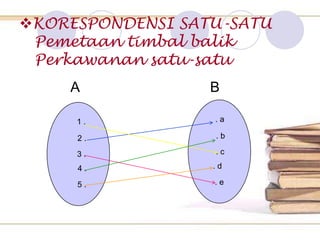
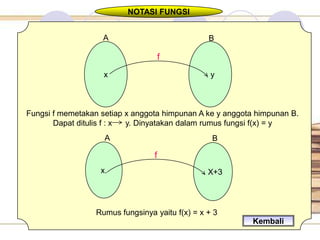
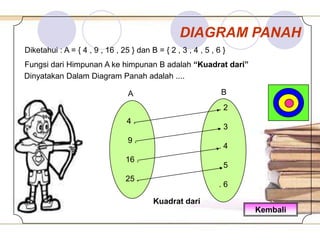
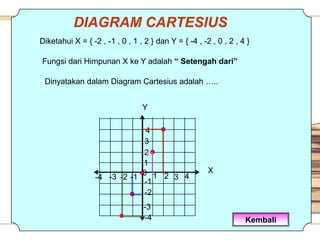
Dokumen ini membahas tentang pemahaman fungsi matematika, termasuk definisi, jenis-jenisnya, dan cara menggambarkannya dalam grafik dan tabel. Diberikan pula contoh-contoh yang menjelaskan korespondensi antara himpunan dan pemetaan satu-satu. Tujuan pembelajaran mencakup pemahaman relasi dan masalah sehari-hari yang berkaitan dengan fungsi.

1. KELAS VIII SMP
MULAI
( Klik Tombol Mulai Untuk menjalankan Program )
Klik Esc pada Keyboard untuk mengakhiri Program

2. TUJUAN PEMBELAJARAN
 Menjelaskan dengan kata-kata dan menyatakan
masalah sehari-hari yang berkaitan dengan fungsi
 Menyatakan suatu fungsi yang terkait dengan kejadian
sehari-hari
 Menggambar grafik fungsi dalam koordinat cartesius
 Menghitung nilai suatu fungsi
 Menyusun tabel fungsi
 Menghitung nilai perubahan fungsi jika variabel berubah
 Menentukan bentuk fungsi jika nilai dan data fungsi
diketahui

3. FUNGSI
Masalah Sehari-hari
Yang berkaitan
Fungsi
Tujuan Pembelajaran
Pengertian
Menyatakan Fungsi
Kembali

4. Masalah Sehari-hari berkaitan fungsi
Perhatikan Gambar
Hubungan / relasinya adalah dimakan
ANI Basket INDONESIA
RAKA Volly MALAYSIA
DANANG Sepak Bola JAPAN
Hubungan antara keduanya Hubungan antara keduanya
adalah “HOBBY” adalah “BENDERA DARI”
Kembali

5. PENGERTIAN FUNGSI
A B
Toba .
. Jawa
Singkarak .
. Sumatera
Poso .
. Kalimantan
Batur . . Sulawesi
Towuti . . Bali
Fungsi adalah relasi khusus yang memasangkan setiap anggota A
dengan tepat satu anggota B
Fungsi dari Himpunan A ke B adalah “Terletak di”

6. ISTILAH – ISTILAH DALAM FUNGSI
 Himpunan A = {Toba, Singkarak, Poso, Batur, Towuti}
Disebut juga Daerah asal (domain)
 Himpunan B = {Jawa, Sumatra, Kalimantan, Sulawesi, Bali}
Disebut juga Daerah Kawan ( Kodomain )
 {Sumatra, Sulawesi, Bali} = Daerah Hasil atau Range

7. BANYAK PEMETAAN DARI DUA HIMPUNAN
NO. n(A) n(B) Banyak pemetaan dari Banyak pemetaan dari
A ke B B ke A
1. 2 1 ......
1 ....
2
2. 1 2 2 1
4 4
3. 2 2 8
4. 2 3 9
5. 3 2
6. 3 3
7. 4 3
8. 3 4
9. .... .....
10. x y n(A) n(B)
11. n(A) n(B) n(B)
................... n(A)
............................

8. KORESPONDENSI SATU-SATU
Pemetaan timbal balik
Perkawanan satu-satu
A B
1. .a
2. .b
3. .c
4. .d
5. .e

9. Himpunan A dikatakan
“berkorespondensi satu-satu”
dengan himpunan B...jika
...setiap anggota A dipasangkan dengan tepat
satu anggota B, dan setiap anggota B
dipasangkan dengan tepat satu anggota A
n(A) = n(B)
Banyak Korespondensi Satu-satu :
..jika n(A) = n(B) = n adalah n x (n-1) x (n-2) x (n-3).... X 3 x 2 x 1 atau
1 x 2 x 3 x ... x (n-2) x (n-1) x n
Kembali

10. NOTASI FUNGSI
A B
f
x .y
Fungsi f memetakan setiap x anggota himpunan A ke y anggota himpunan B.
Dapat ditulis f : x y. Dinyatakan dalam rumus fungsi f(x) = y
A B
f
x. . X+3
Rumus fungsinya yaitu f(x) = x + 3
Kembali

11. VARIABEL BEBAS DAN VARIABEL BERGANTUNG
Dalam persamaan grafik fungsi y = f(x) = ax + b,
Jika nilai x berubah, maka nilai y = f(x) akan berubah nilainya
x pada ax disebut variabel bebas
y = f(x) disebut variabel tergantung

12. GRAFIK FUNGSI
Contoh 1.
 Buatlah daftar untuk fungsi x (½).x + 1
dari himpunan {0, 2, 4, 6, 8} ke himpunan bilangan cacah.
 Gambarlah grafik fungsi
 Gambarlah grafik fungsinya pada himpunan bialangan positif
dan nol
Contoh 2 .
 Buatlah daftar untuk fungsi g:x x2 + 1 dari himpunan {0, 1, 2,
3, 4) ke himpunan bilangan cacah
 Buatlah grafik dari fungsi itu, kemudian gambarlah kurva mulus
melalui titik-titik itu.

13. MENYATAKAN FUNGSI
Dengan Dengan Dengan Himpunan
Diagram Panah Grafik Cartesius Pasangan Berurutan
( Klik Pilihan yang diinginkan )
Kembali

14. DIAGRAM PANAH
Diketahui : A = { 4 , 9 , 16 , 25 } dan B = { 2 , 3 , 4 , 5 , 6 }
Fungsi dari Himpunan A ke himpunan B adalah “Kuadrat dari”
Dinyatakan Dalam Diagram Panah adalah ....
A B
.2
4.
.3
9.
.4
16 .
.5
25 .
.6
Kuadrat dari
Kembali

15. DIAGRAM CARTESIUS
Diketahui X = { -2 , -1 , 0 , 1 , 2 } dan Y = { -4 , -2 , 0 , 2 , 4 }
Fungsi dari Himpunan X ke Y adalah “ Setengah dari”
Dinyatakan dalam Diagram Cartesius adalah …..
Y
4
3
2
1
0 1 2 X
-4 -3 -2 -1 3 4
-1
-2
-3
-4 Kembali

16. Himpunan Pasangan Berurutan
Diketahui C = { 3 , 5 , 7, 9 } dan D = { 6 , 14 , 16 , 20 , 32 , 54 }
Fungsi dari Himpunan C ke D adalah “ faktor dari”
Dinyatakan dalam Himpunan Pasangan Berurutan adalah …
3 Dipasangkan ke 6
Ditulis
5 Dipasangkan ke 20
{ (3,6) , (5,20) , (7,14) , (9,54) }
7 Dipasangkan ke 14
9 Dipasangkan ke 54
Kembali