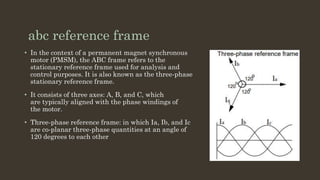
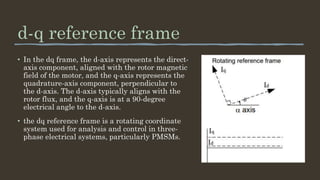
Reference frame theory provides a mathematical framework to analyze and control permanent magnet synchronous motors by transforming three-phase variables into rotating reference frames like the dq frame. This simplifies analysis and enables techniques like field-oriented control. The Clarke and Park transformations convert variables between stationary abc/αβ frames and the rotating dq frame. Clarke transforms from abc to αβ, and Park transforms between αβ and dq frames through rotation by the electrical angle. Transforming variables allows decoupling dynamics and more efficient analysis and control of electric machines.

1. REFERENCE FRAME THEORY

2. • Introduction
• Reference frames
1. Abc frame
2. αβ frame
3. Dq frame
• Transformations
• Advantages of transformation
• Clarke and inverse clarke
transformations
• Park and inverse park
transformations
• Abc to dq transformation

3. Introduction
Reference frame theory is a
mathematical framework used to analyze
and control the behavior of a permanent
magnet synchronous motor (PMSM). It
provides a convenient way to transform the
motor's three-phase variables into two
orthogonal axes, simplifying the analysis
and control of the motor. The reference
frame is a coordinate system used to
represent the electrical variables of the
motor.

4. abc reference frame
• In the context of a permanent magnet synchronous
motor (PMSM), the ABC frame refers to the
stationary reference frame used for analysis and
control purposes. It is also known as the three-phase
stationary reference frame.
• It consists of three axes: A, B, and C, which
are typically aligned with the phase windings of
the motor.
• Three-phase reference frame: in which Ia, Ib, and Ic
are co-planar three-phase quantities at an angle of
120 degrees to each other

5. α-β-0
reference
frame
• The alpha-beta reference frame, also known
as the two-phase stationary reference frame,
is a coordinate system commonly used in the
analysis and control of three-phase electrical
systems, including permanent magnet
synchronous motors (PMSMs).
• Orthogonal stationary reference frame: in
which Iα (along α axis) and Iβ (along β axis)
are perpendicular to each other, but in the
same plane as the three-phase reference
frame

6. • the alpha-beta reference
frame is a two-phase
stationary reference
frame obtained by
rotating the ABC frame
by 30 degrees.

7. d-q reference frame
• In the dq frame, the d-axis represents the direct-
axis component, aligned with the rotor magnetic
field of the motor, and the q-axis represents the
quadrature-axis component, perpendicular to
the d-axis. The d-axis typically aligns with the
rotor flux, and the q-axis is at a 90-degree
electrical angle to the d-axis.
• the dq reference frame is a rotating coordinate
system used for analysis and control in three-
phase electrical systems, particularly PMSMs.

8. • The combined
representation of the
quantities in all
reference frames is
shown in Figure

9. Transformation
• The process of replacing one set of variables by another related set of variables is
called transformation.
• In the study of power systems and electric machine analysis,
mathematical transformations are often used to decouple variables, to facilitate the
solution of difficult equations with time-varying coefficients or to refer all variables to
a common reference frame.
• There are mainly two types of transformation.
1. Clarke transformation
2. Park transformation

10. Advantages of reference frame
transformation
• By transforming variables into these reference frames, engineer
can decouple the stator and rotor dynamics and analyze and control the
electric machine efficiently.
• The number of voltage equations are reduced
and time varying voltage equations become time invariant ones.
• It enables the application of techniques such as field-oriented control(FOC) where
machine variables are controlled along the d-q axes, allowing independent
of control of torque and flux.

11. Clarke transformation
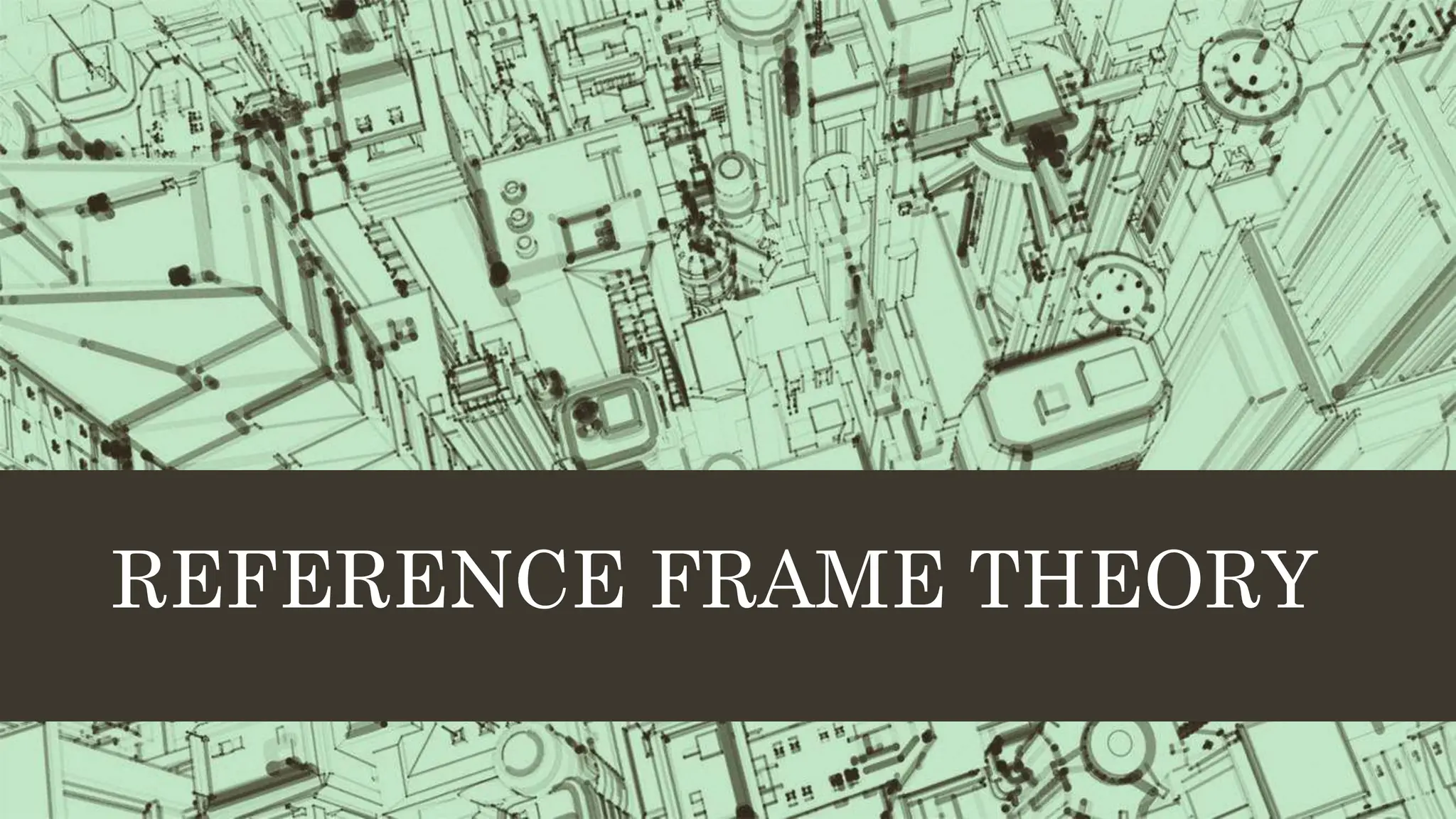
• The Clarke Transformation converts the time-domain components of a three-phase system in an
abc reference frame to components in a stationary ɑβ0 reference frame..
• This can preserve the active and reactive powers of the system in the abc frame.
• In order for the transformation to be invertible, a third variable, known as the zero-
sequence component, is added.
• The resulting transformation equation is given by
[ fαβ0 ] = T αβ0 [ fabc ]
Where f represents voltage, current, flux linkage or electric charge

12. where
1 -½ -½
Tαβ0 = 2/3 0 √3/2 -√3/2
½ ½ ½
fa fα
fabc = fb fαβ0 = fβ
fc f0

13. • 𝐼𝛼 = 2/3 (𝐼𝑎) − 1/3 (𝐼𝑏 − 𝐼𝑐)
• 𝐼𝛽 = 2 /√3 (𝐼𝑏 − 𝐼𝑐)
where,
Ia, Ib, and Ic are three-phase quantities and
Iα and Iβ are stationary orthogonal reference frame quantities
• When Iα is superposed with Ia and Ia + Ib + Ic is zero,
Ia, Ib, and Ic can be transformed to Iα and Iβ as:
• 𝐼𝛼 = 𝐼𝑎
• 𝐼𝛽 = 1 √3 (𝐼𝑎 + 2𝐼𝑏) where Ia + Ib + Ic = 0

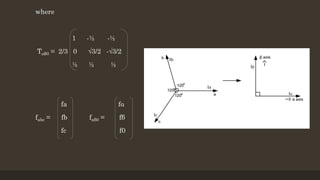
14. Inverse clarke transformation
• The transformation from a two-axis orthogonal stationary reference frame to a three-
phase stationary reference frame is accomplished using Inverse Clarke
transformation a. The Inverse Clarke transformation is expressed by the following
equations:
[ fabc ] = T αβ0
-1 [ fαβ0 ]
1 0 1
Where Tαβ0
-1 = -½ √3/2 1
-½ -√3/2 1

15. Park's transformation
• This transformation converts vectors in balanced two-phase orthogonal stationary
system into orthogonal rotating reference frame.
• 𝐼𝑑 = 𝐼𝛼 ∗ cos(𝜃) + 𝐼𝛽 ∗ sin(𝜃)
• 𝐼𝑞 = 𝐼𝛽 ∗ cos(𝜃) − 𝐼𝛼 ∗ sin(𝜃)
Where,
Id, Iq are rotating reference frame quantities
Iα, Iβ are orthogonal stationary reference frame
quantities
θ is the rotation angle
• θ = ω dt where w is angular velocity

16. Inverse Park Transformation
• The quantities in rotating reference frame are transformed to two-axis orthogonal
stationary reference frame using Inverse Park transformation. The Inverse Park
transformation is expressed by the following equations:
• I𝛼 = I𝑑 ∗ cos(𝜃) − I𝑞 ∗ sin(𝜃)
• I𝛽 = I𝑞 ∗ cos(𝜃) + I𝑑 ∗ sin(𝜃)
where,
Iα, Iβ are orthogonal stationary reference frame quantities and
Id, Iq are rotating reference frame quantities

17. Abc to dq transformation
• This component performs the ABC to DQ0 transformation, which is a cascaded
combination of Clarke's and Park's transformations.
• The transformations equations are as follows:
• Id = 2/3 ( Ia*sin(ωt) + Ib*sin(ωt−2π/3) + Ic*sin(ωt+2π/3) )
• Iq = 2/3 ( Ia*cos(ωt) + Ib*cos(ωt−2π/3) + Ic*cos(ωt+2π/3) )
• I0 = 1/3 ( Ia + Ib + Ic )

18. abc αβ0 dqo