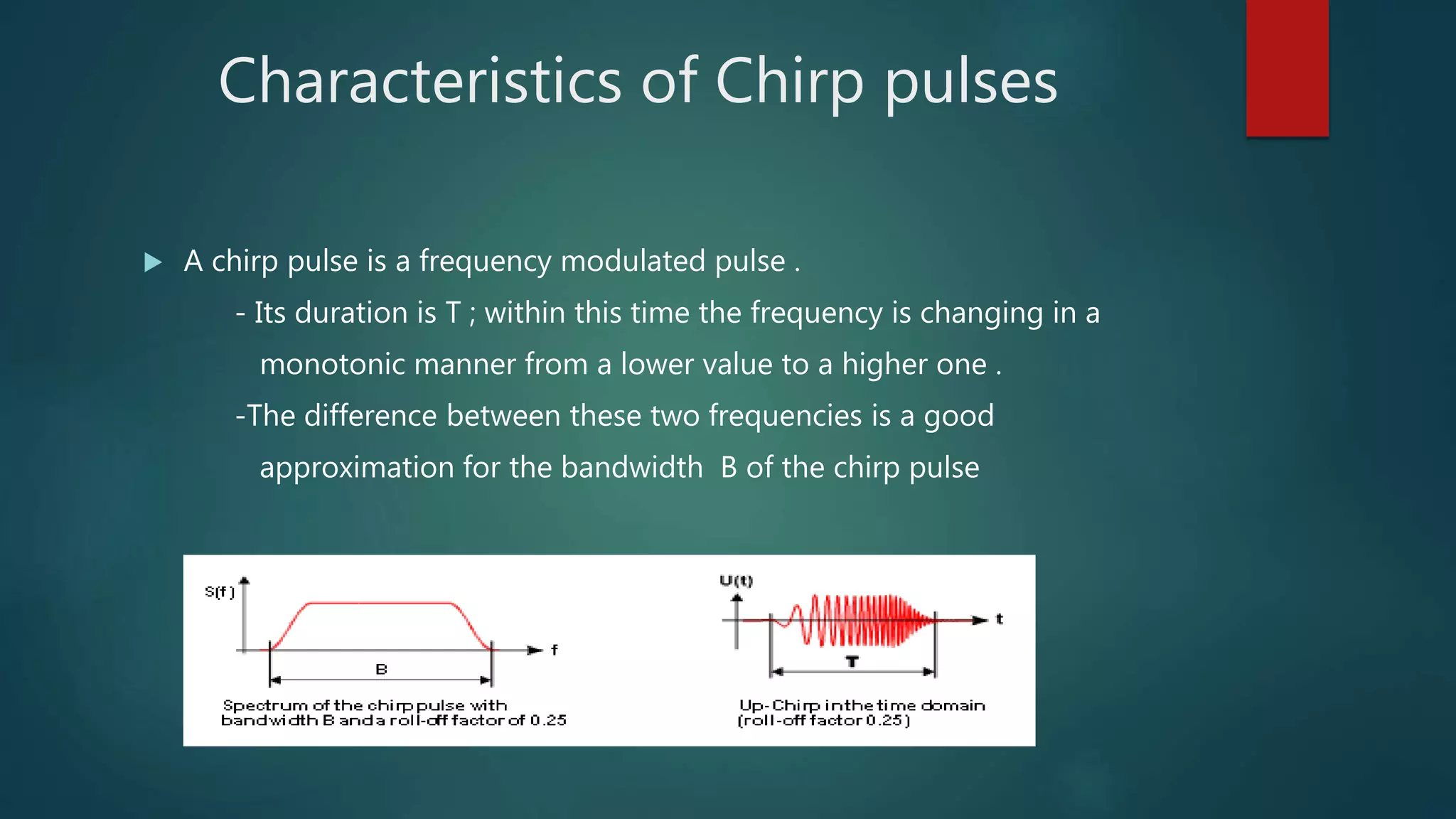
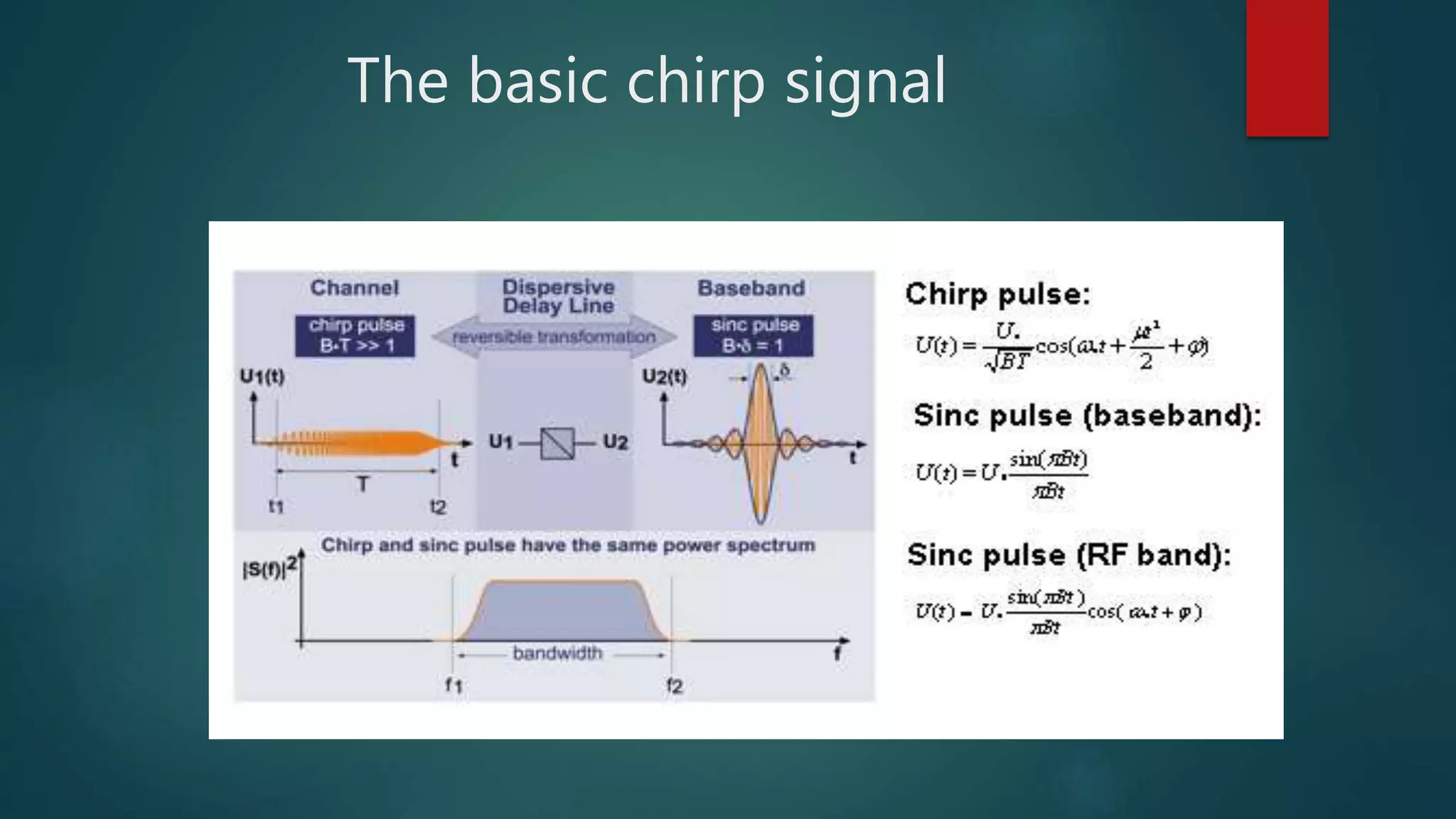
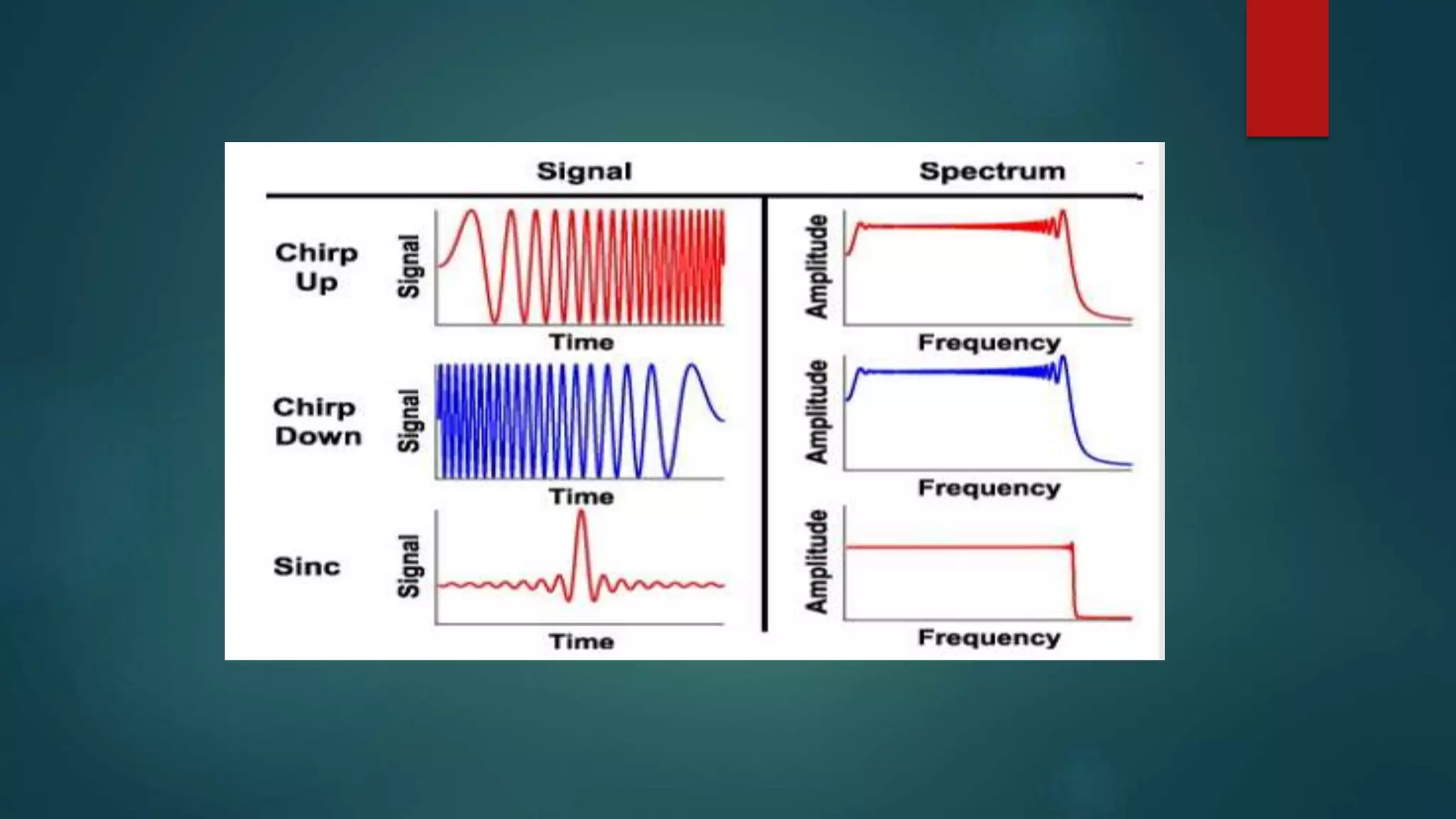
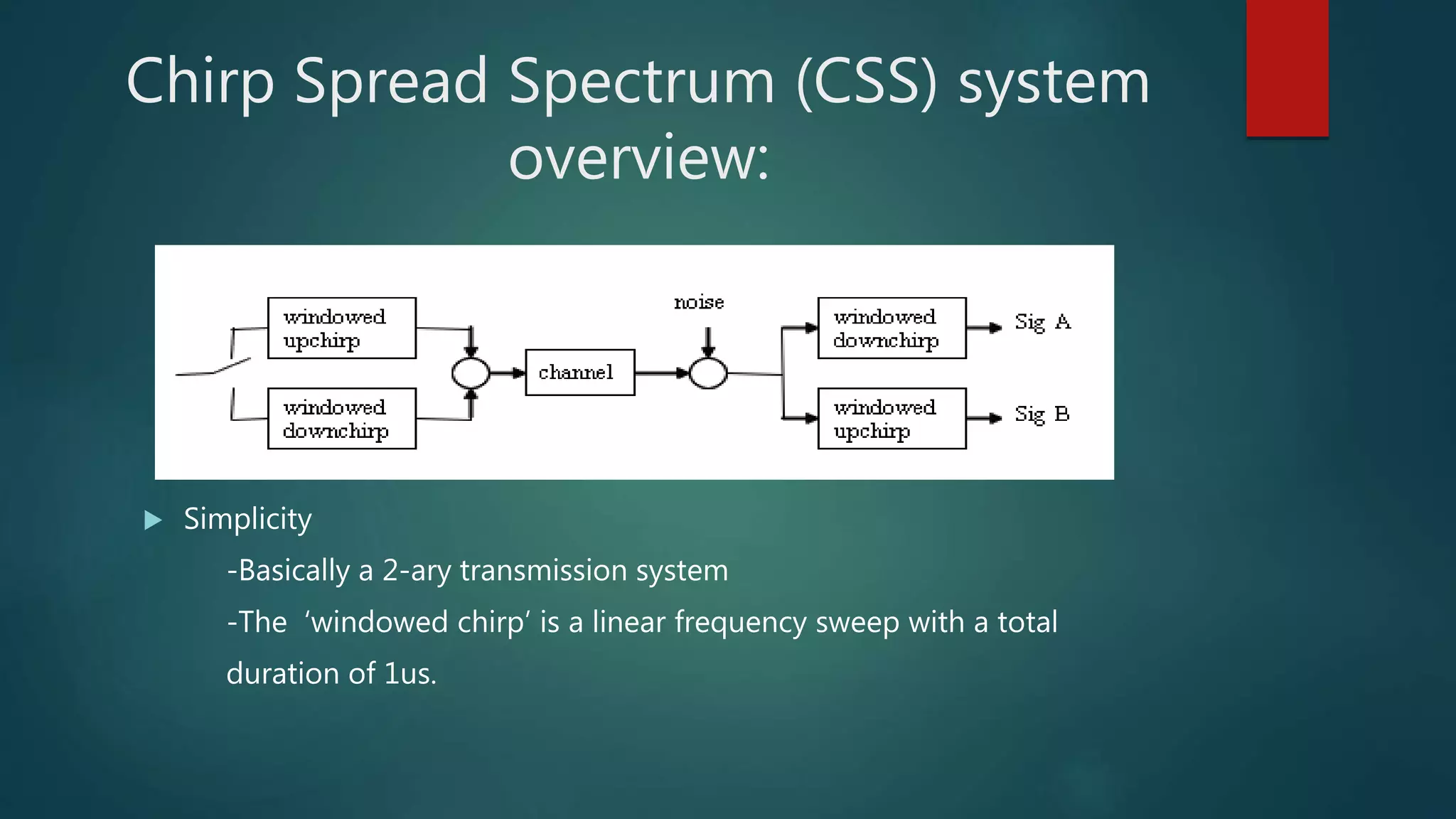
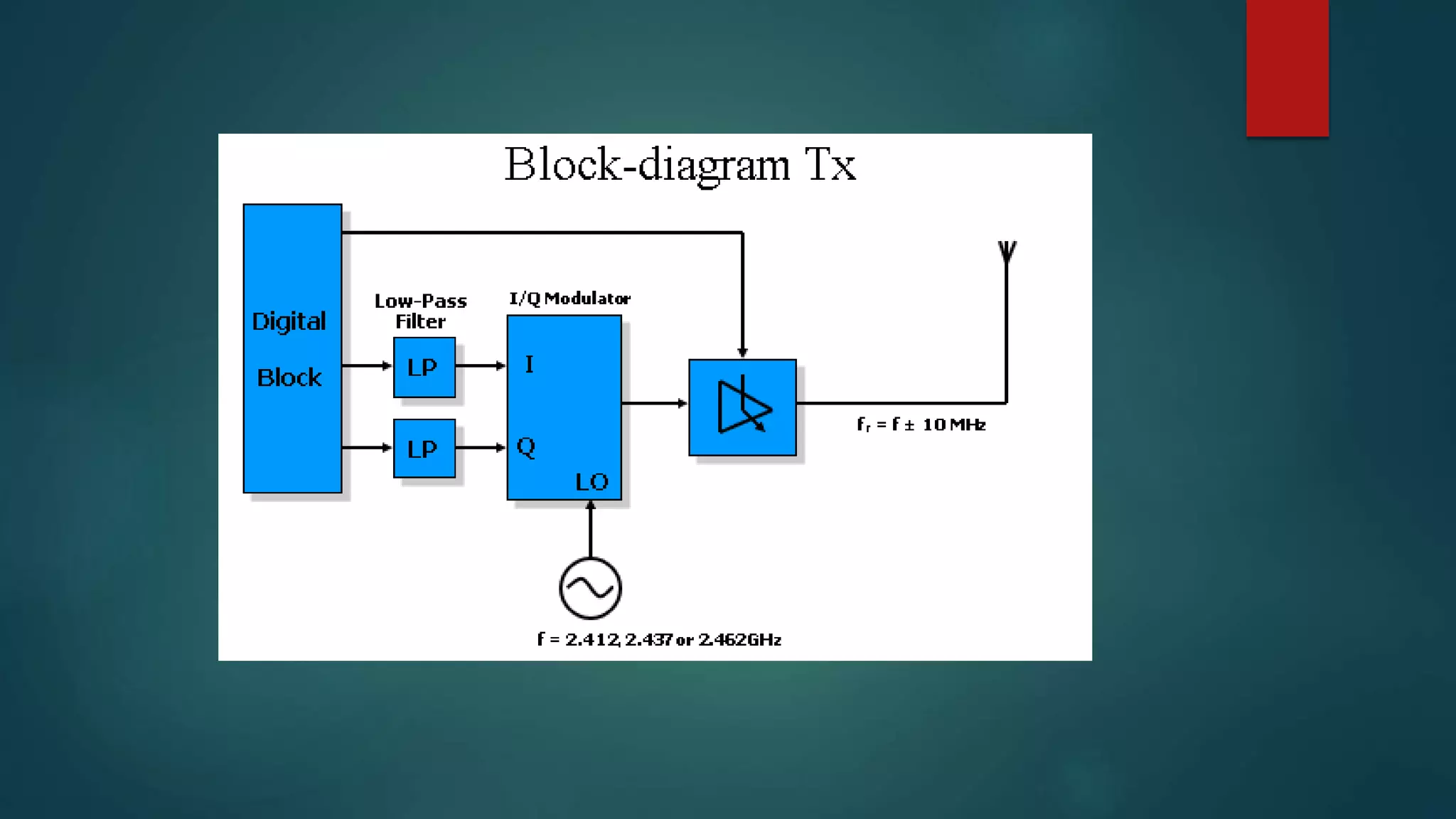
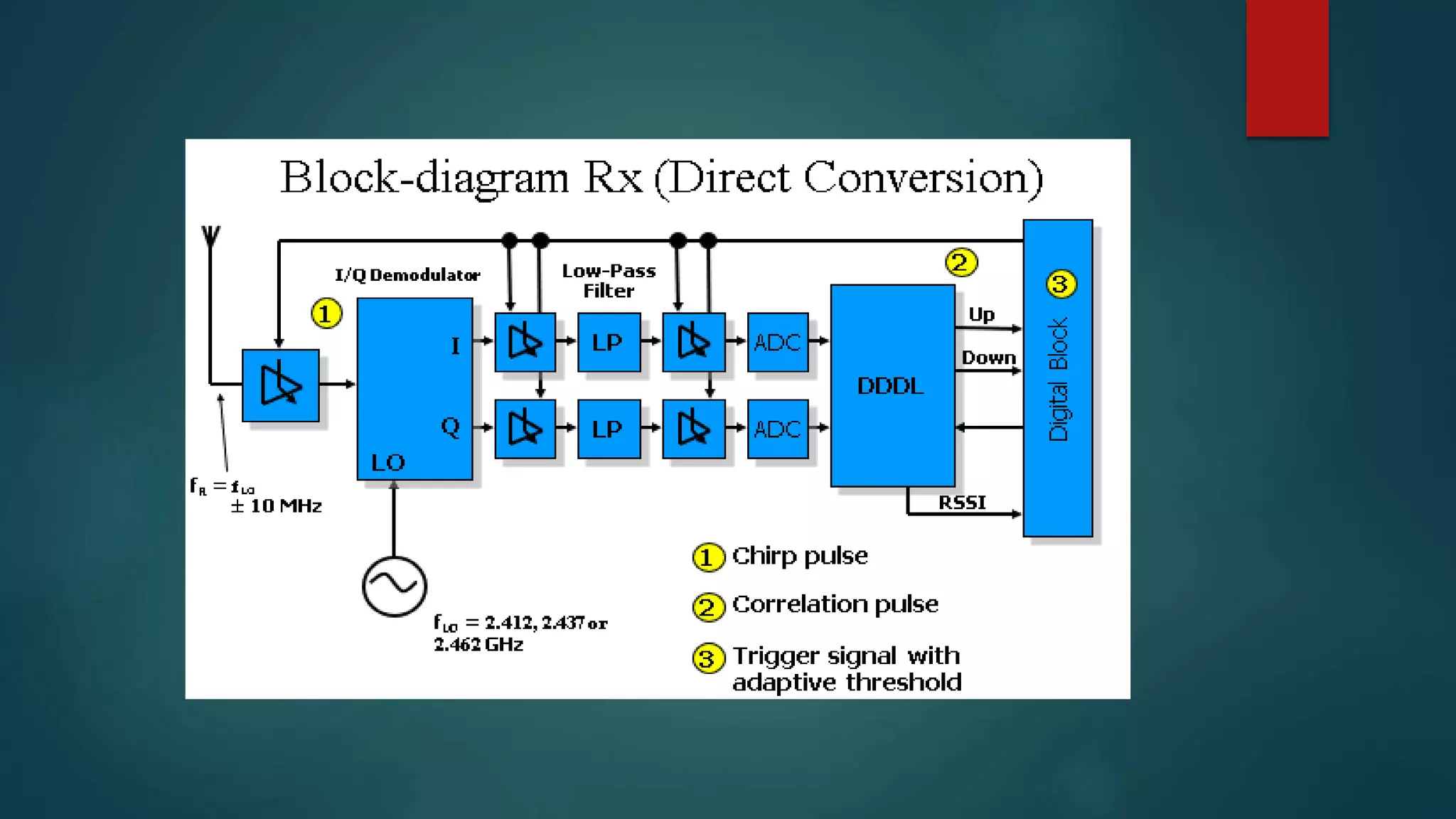
This document discusses Chirp Spread Spectrum (CSS) communication. It defines key terms like spectrum, spread spectrum, and chirps. It explains that chirps are signals where frequency increases or decreases over time. CSS uses chirp signals that are spread over a wide bandwidth for communication. It provides several benefits - high robustness against interference due to its wide bandwidth, resistance to multipath fading and Doppler shift, low power consumption, and low latency.

1. Chirp Spread
Spectrum
Communication
Presented By-
Mahmudul Islam (1506155)
Mohammad Abdul Mobin (1506006)

2. Spectrum
 “spectrum” is a general term to encompass the spatial and temporal
properties of any medium , including fiber optic cable , coaxial cable , and
ambient air.

3. Spread Spectrum
• Spread-spectrum techniques are methods by which a signal
(e.g an electrical , electromagnetic, or acoustic signal generated in
a particular bandwidth is deliberately spread in the frequency
domain , resulting in a signal with a wider bandwidth.)
• These techniques are used for varieties of reasons , including
a . The establishment of secure communications
b. increasing resistance to natural interference, noise
c. jamming , to prevent detection , and
d. to limit power flux density (e.g. in satellite downlinks)

4. Chirp
• A short, high-pitched sound , such as that made by a small bird or an
insect.
• The sound emitted by crickets is commonly referred to as chirping.
• The specificity of bird calls has been used extensively for species
identification.
• The calls of birds have been described using words or nonsense syllables
or line diagrams.
• Common terms in English include words such as quack,chirp

5. Chirp(conc.)
 A chirp is a signal in which frequency increased (‘up-chirp’) or decreases
(‘down-chirp’) with time .
 In some sources , the term chirp is used interchangeably with sweep
signal .
 It is commonly used in sonar and radar , but has other applications , such
as in spread spectrum communications.
 In spread spectrum usage , SAW devices such as RACs are often used to
generate and demodulate the chirped signals .
 In optics , ultrashort laser pulses also exhibit chirp , which , in optical
transmission systems interacts with the dispersion properties of the
materials , increasing or decreasing total pulse dispersion as the signal
propagates .

6. A chirp signal waveform can be written as
S(t) = a(t) cos[θ(t)]
Where θ(t) is the phase and a(t) is the envelope of the chirp signal which is zero outside a
time interval of length T.
The instantaneous frequency is defined as
fM (t) =
1
2𝜋
𝑑θ
𝑑𝑡
The chirp rate is defined by
µ(t) =
𝑑fM
𝑑𝑡
=
1
2𝜋
𝑑2θ
𝑑𝑡2
and represents the rate of change of the instantaneous frequency.
Chirp(conc.)

7.  When µ (t) > 0 then the signal is called up-chirps
 When µ (t) < 0 then the signal is called down-chirps
 For a linear chirp µ (t) is constant, and hence fM (t) is a linear
function of t, and θ(t) is a quadratic function those with.
If we take the waveform to be centered at t = 0 it can be written as
s(t) = a(t) cos [2𝜋f0t + 𝜋µ𝑡2
+ φ0 ]
where fc is the center frequency and a(t) = 0 for |t| > T/2
It is convenient to define the bandwidth B as the range of the instantaneous
frequency, so that
B =| µ |T
Chirp(conc.)

8.  The impulse response of a matched filter for a linear chirp signal is again a linear chirp
signal but with a chirp rate of opposite sign.
 If a chirp waveform is fed into its matched filter the output signal typically has a
narrow IF peak at the chirp center frequency.
 If we consider chirp waveforms with at time domain envelopes and take the matched
filter to be centered at t = 0 we find an analytical expression for the output waveform
g(t) of the matched filter.
Chirp(conc.)

9. g(t) = h(t)*s(t)= φss (t)
Where φss (t) is the autocorrelation function of s(t). It can be shown that φss (t) is given by that
for T < t < T . The envelope has its maximum at t = 0, and its first zeros at t≈±1/B. It is therefore
convenient
to specify the pulse width as 1/B. The ratio of the input and output pulse widths is therefore given by
the time-bandwidth product TB which is known as compression ratio or processing gain.
Another important parameter is the sidelobe rejection, which is about 13 dB for a chirp signal
where a(t) has rectangular shape. A common method of reducing the sidelobes is to apply amplitude
weighting of the chirp signals

10. Characteristics of Chirp pulses
 A chirp pulse is a frequency modulated pulse .
- Its duration is T ; within this time the frequency is changing in a
monotonic manner from a lower value to a higher one .
-The difference between these two frequencies is a good
approximation for the bandwidth B of the chirp pulse

11. The basic chirp signal

12. Chirp Modulation
 Chirp modulation was patented by Sidney Darlington in 1954 with
significant later work performed by Winkler in 1962.
 This type of modulation employs sinusoidal waveforms whose
instantaneous frequency increases or decreases linearly over time . These
waveforms are commonly referred to as linear chirps or simply chirps .
 Hence the rate at which their frequency changes is called the “chirp rate”.
 In birnary chirp modulation , binary data is transmitted by mapping the
bits into chrips of opposite chirp rates. For instance, over one bit period “1”
is assigned a chrip with positive rate a and “0” a chirp with negative rate –
a .

14. Chirp Spread Spectrum (CSS) system
overview:
 Simplicity
-Basically a 2-ary transmission system
-The ‘windowed chirp’ is a linear frequency sweep with a total
duration of 1us.

17. Key Properties of Chirp Spread
Spectrum (CSS)
• High robustness:
Due to the high BT product ,chirp pulses are very resistant
against disturbances
• Multipath resistant:
Due to the broadband chirp pulse , CSS is very immune against
multipath fading; CSS can ever take advantage of RF echoes.
• Low power consumption:
CSS allows the designer to choose an analog implementation ,
which often consumes much less power.
• Low latency :
CSS needs no synchronization ; a wireless connection can be
established very quickly.

18. Mobility Properties of CSS
 Resistance against Doppler effect :
The Doppler effect causes a frequency shift of the chirp pulse ,
Which introduces a negligible shift of the baseband signal on the time axis.

19. Coexistence Properties of CSS
 Immune to in-band interferer:
Scalable processing gain (determined by BT product of the chirp)
enables selection fo appropriate immunity level against in-band interferences
.