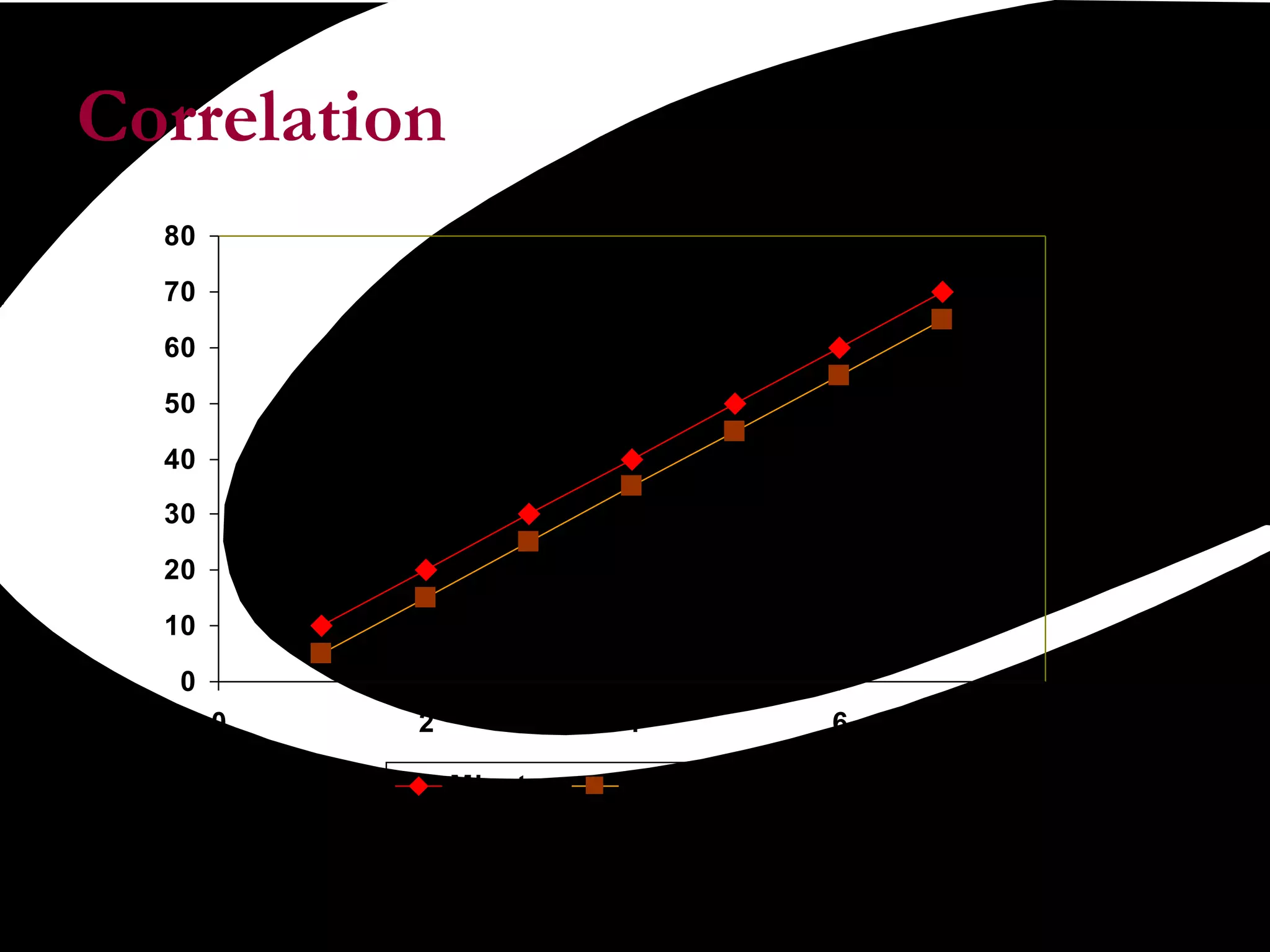
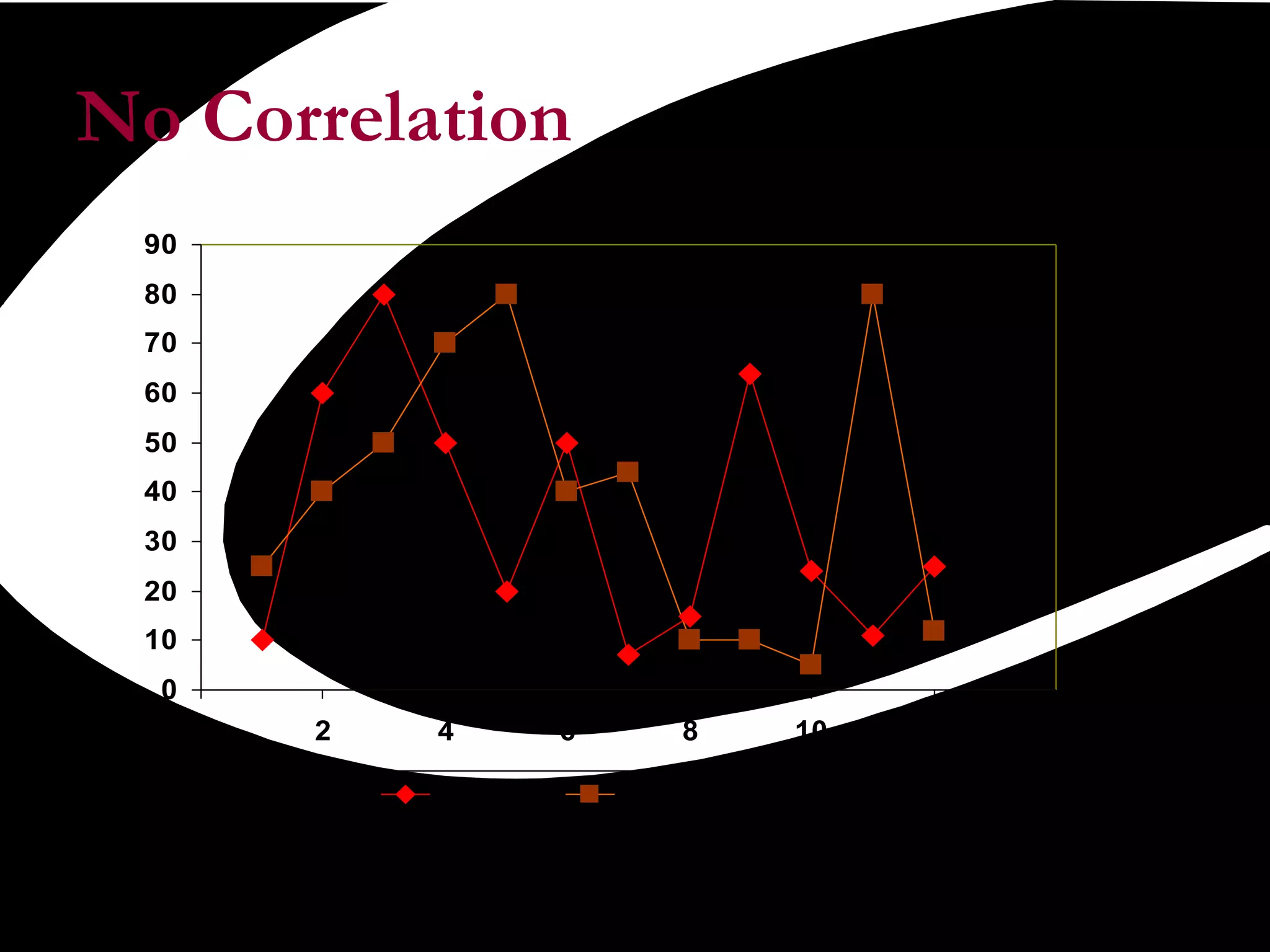
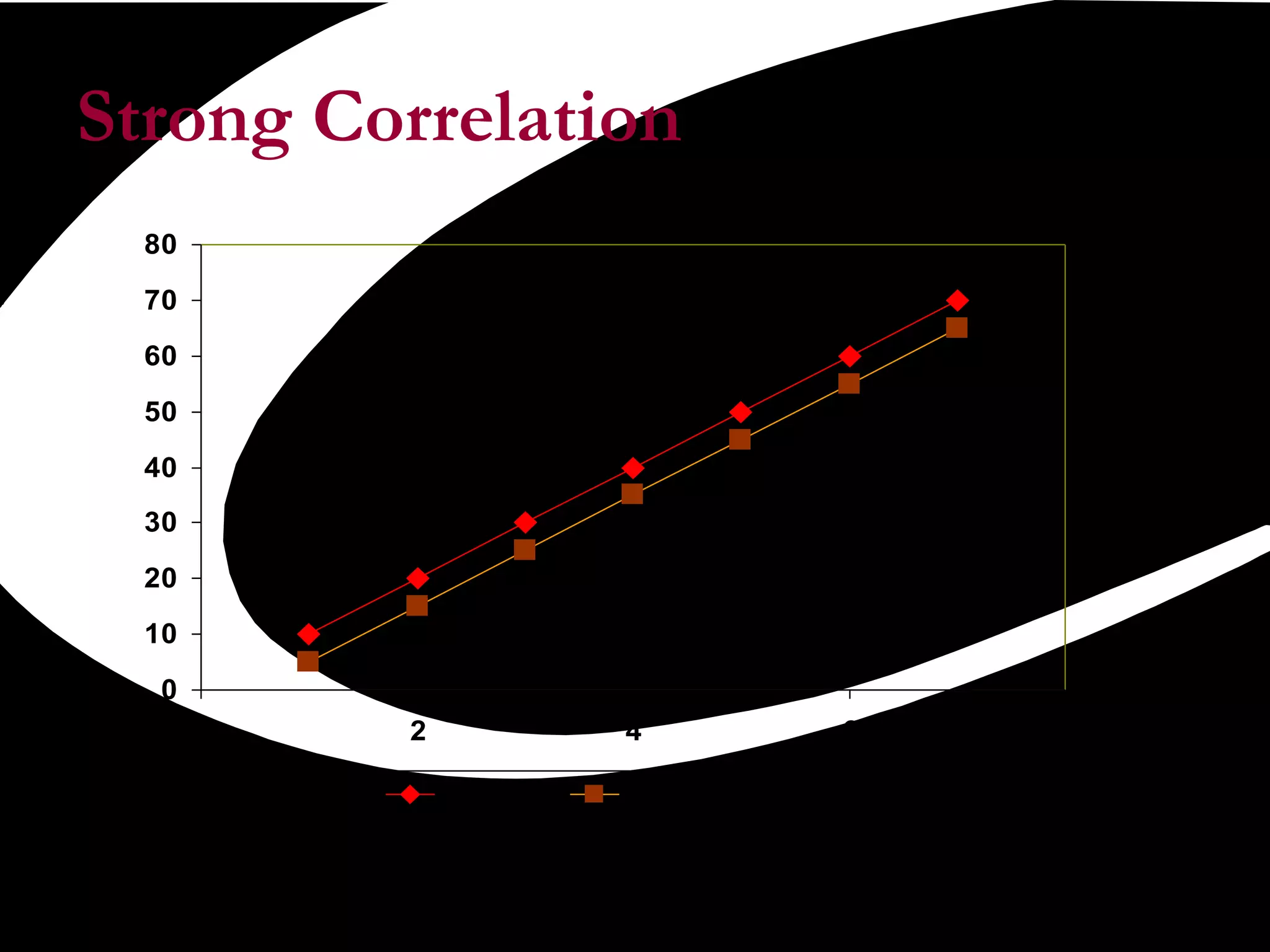
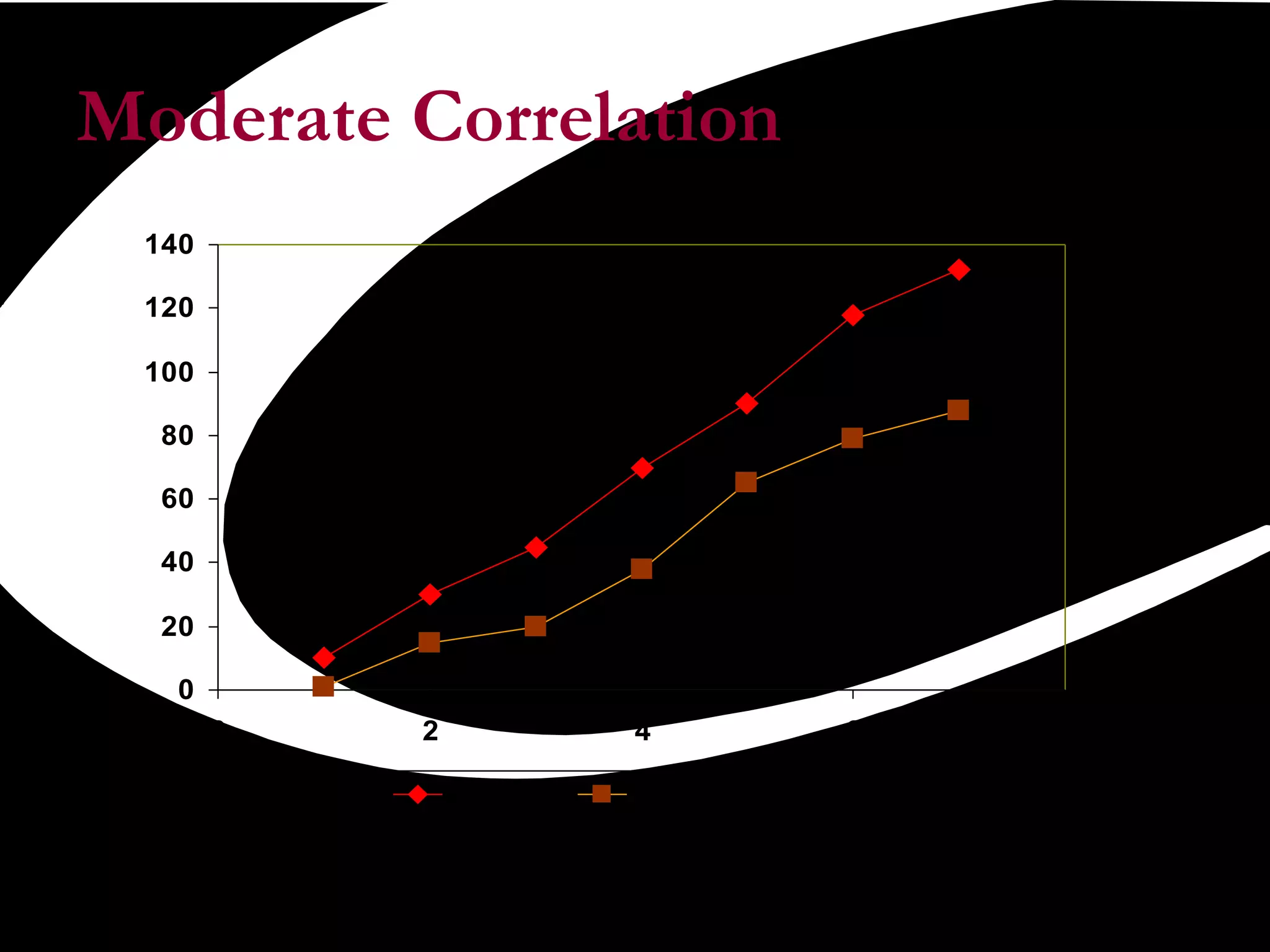
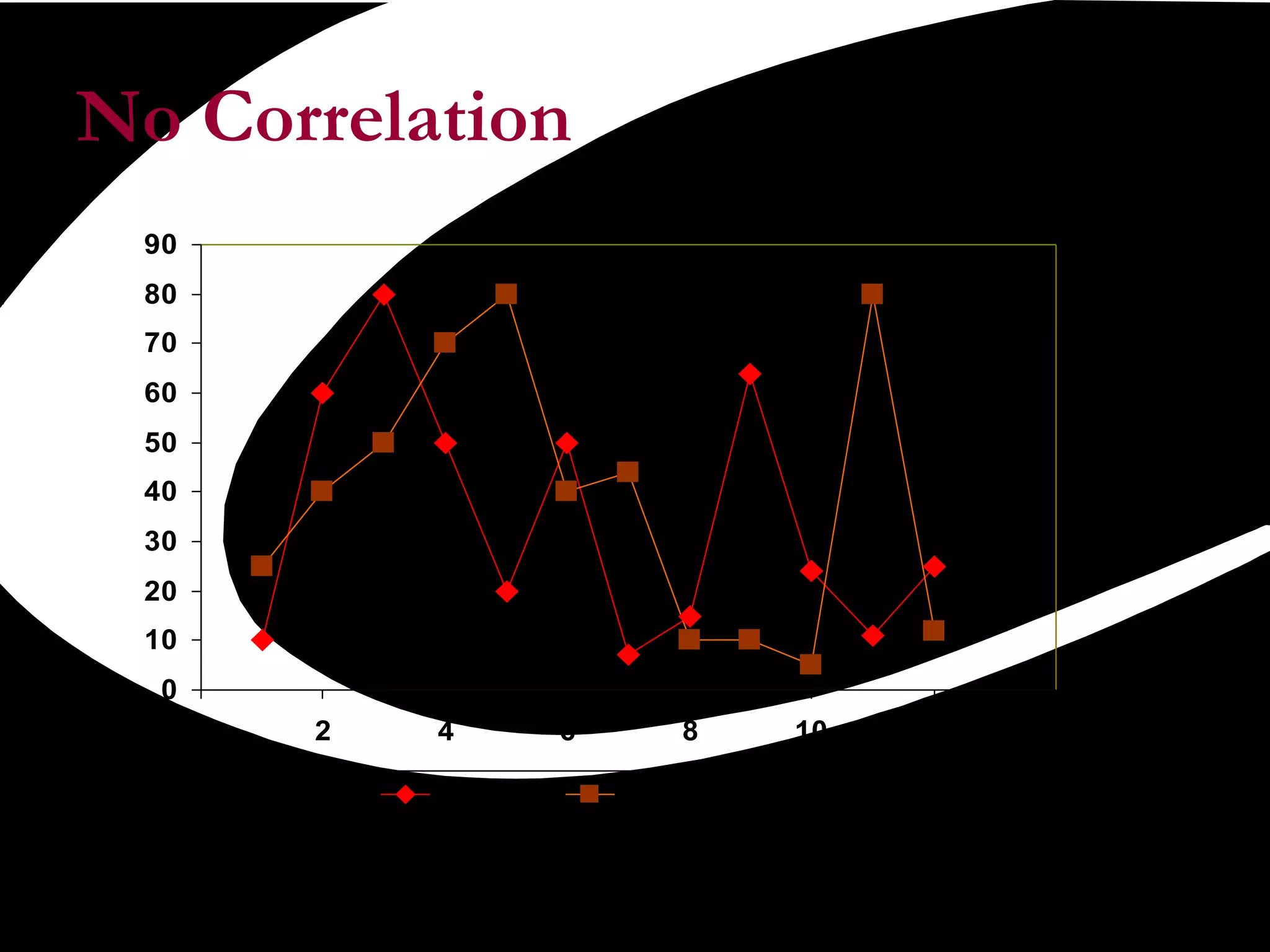
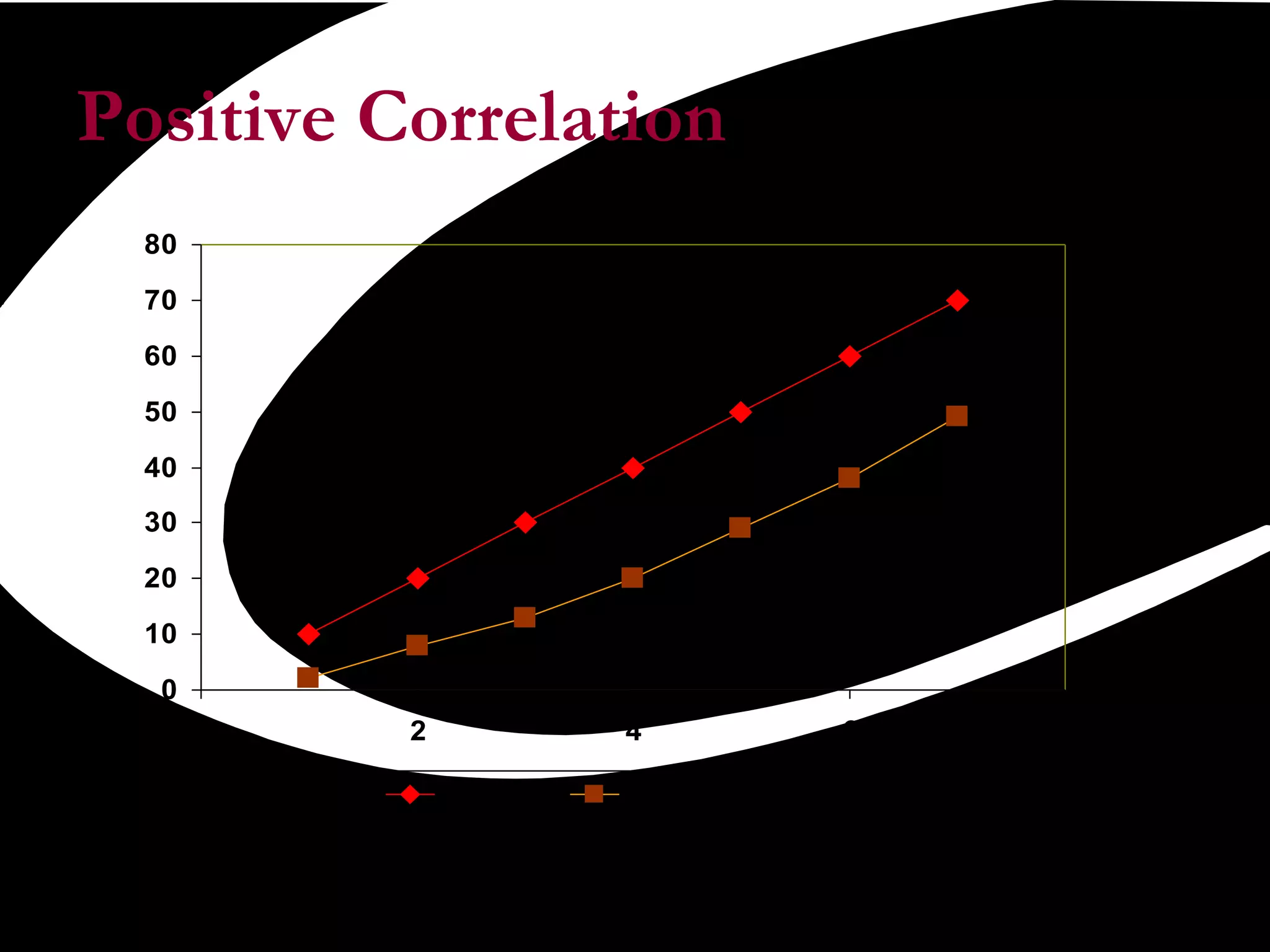
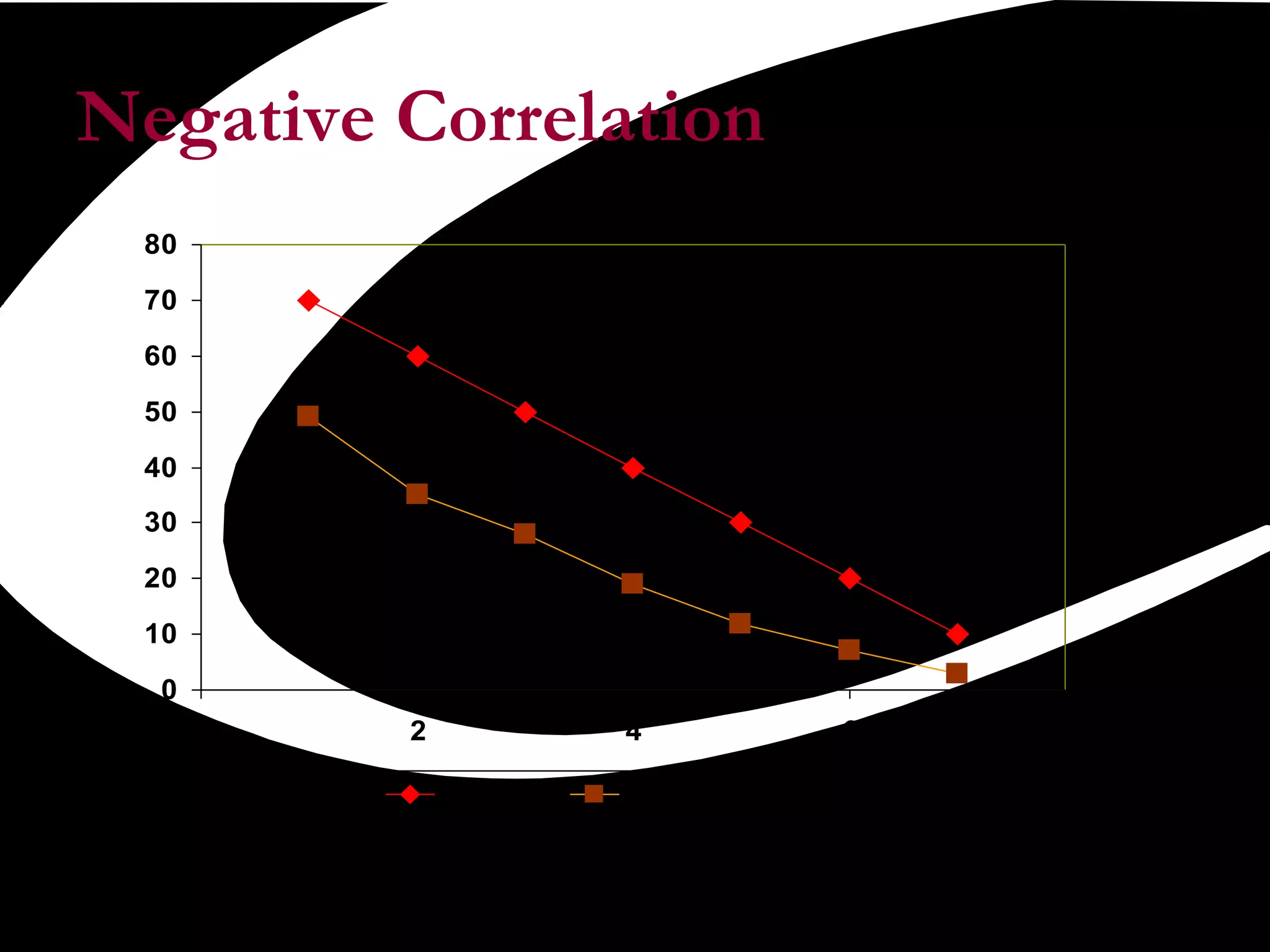
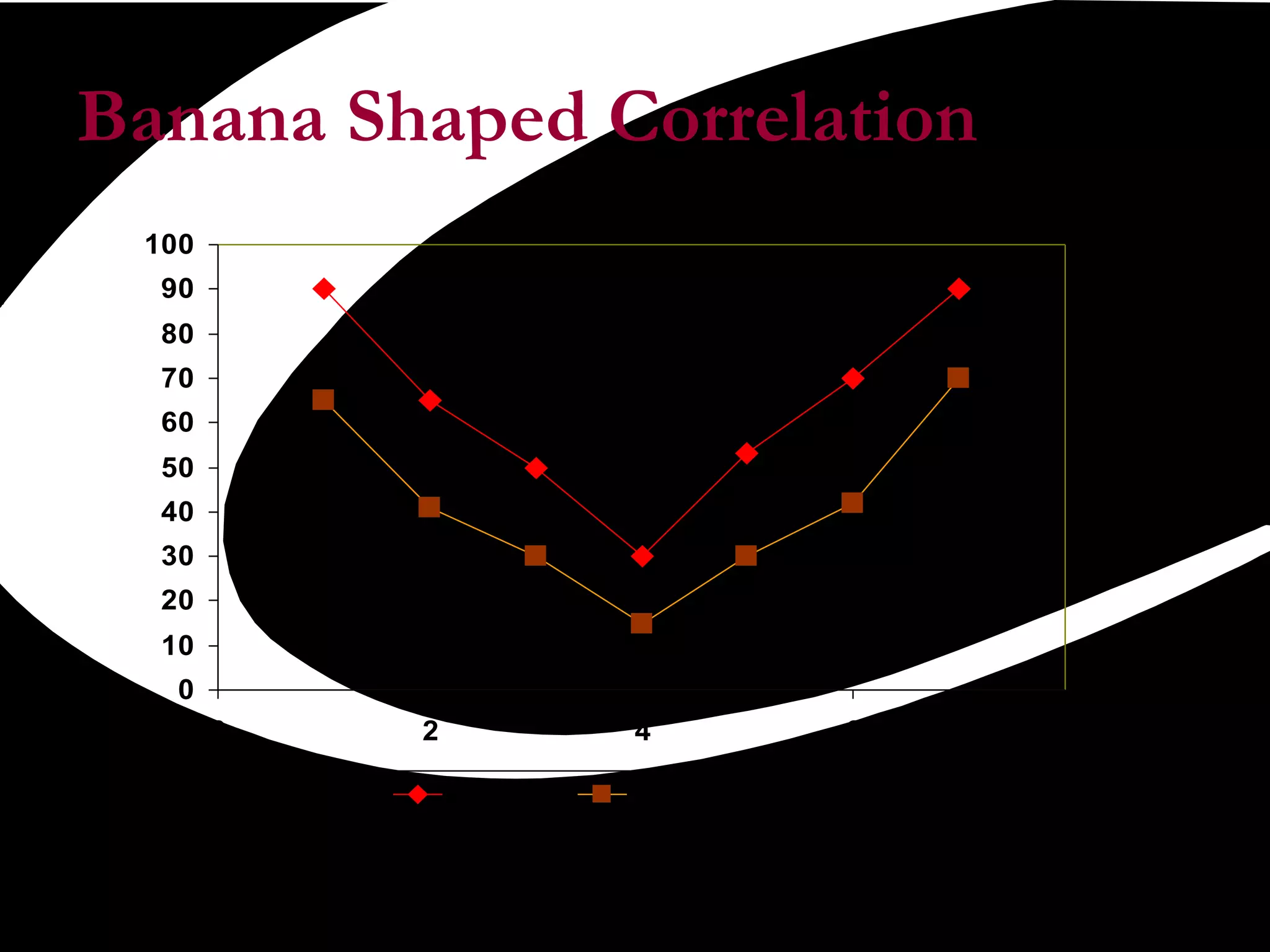
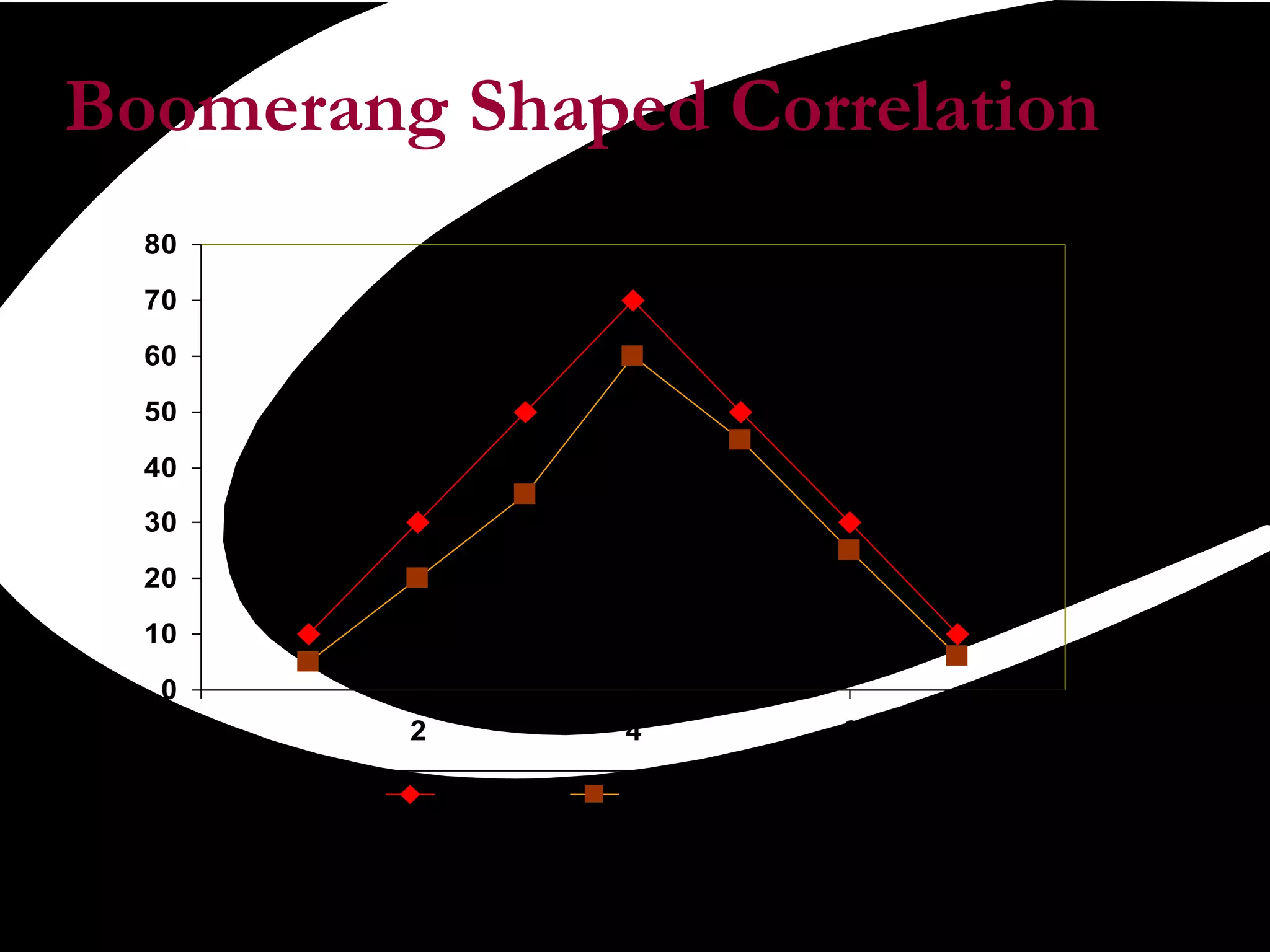
Scatter plots are a quality tool used to show the relationship between two variables. They graph pairs of numerical data with one variable on each axis to look for correlation. If the variables are correlated, the data points will fall along a line or curve, indicating a relationship. Scatter plots are useful for determining potential causes of problems by identifying which process elements are related and how strongly. They involve collecting paired data, plotting the independent variable on the x-axis and dependent variable on the y-axis, and examining the shape and slope of the resulting cluster of points.

1. Scatter Plot Nishant Narendra

2. Content Six Sigma – an introduction Scatter Plot When Why How Example Relationships Summary

3. Six Sigma A statistical measure of variation. Developed by Motorola for the first time in the mid-1980’s. Full Six Sigma equals to 99.9997% accuracy. A ‘tool box’ of quality and management tools for problem resolution. A business philosophy focusing on continuous improvement. An organized process for structured analysis of data.

4. Common Tools Affinity Diagram Kano Model Critical-To-Quality (CTQ) tree Pareto Charts Control Charts Run Charts Failure Modes and Effect Analysis (FMEA) 5 Whys Analysis Brainstorming Cause and Effect (C&E) Diagram Flow Diagrams Scatter Plots

5. Scatter Plot Also called as scatter diagram, scattergram, Correlation Analysis, or X-Y Analysis. It is a basic graphic tool that illustrates the relationship between two variables. Scatter plots are a useful diagnostic tool for determining association, but if such association exists.

6. Scatter Plot The Scatter Diagram is a Quality Tool that can be used to show the relationship between "paired data" and can provide more useful information about a production process.

7. Description The scatter diagram graphs pairs of numerical data, with one variable on each axis, to look for a relationship between them. The dots on the scatter plot represent data points. If the variables are correlated, the points will fall along a line or curve. The better the correlation, the tighter the points will hug the line.

8. When When you have paired numerical data. When your dependent variable may have multiple values for each value of your independent variable. When trying to determine whether the two variables are related, such as… When trying to identify potential root causes of problems. After brainstorming, using a fishbone diagram, to determine objectively whether a particular cause and effect are related. When determining whether two effects that appear to be related both occur with the same cause. When testing for autocorrelation before constructing a control chart.

9. Benefits: Helps identify and test probable causes. By knowing which elements of your process are related and how they are related: You will know what to control. What to vary to affect a quality characteristic.

10. How On gridline or graph paper: STEP #1 Decide which paired factors you want to examine. Both factors must be measurable on some incremental linear scale. Draw an "L" form. Make your scale units at even multiples, such as 10, 20, etc. so as to have an even scale system. Collect 30 to 100 paired data points. Find the highest and lowest value for both variables.

12. On the Horizontal axis (Known as the "X" axis, from Left to Right) you place the Independent or "cause" variable. STEP #2

13. On the Vertical axis (Known as the "Y" axis, from Bottom to Top) you place the Dependent or "effect" variable. STEP #3

14. Plot your data points at the intersection of your data plots of the X and Y values. For Example = X = 5, Y = 2. Go right 5 spaces, and then go up 2 spaces to plot the point (from O, which is the origin point.) The shape that the cluster of dots takes will tell you something about the relationship between the two variables that you tested. STEP #4

15. Example In a bakery the data was gathered for identifying relationship between minutes of cooking and defective pieces. Below mentioned was the sample collected: Minutes Cooking Defective Pies 10 1 45 8 30 5 75 20 60 14 20 4 25 6

16. Scatter Plot

17. Three Parameters for relationship Correlation Slope Direction

18. Correlation Measures how well the data line up. The more the data resembles a straight line, the better the correlation to each other.

19. Correlation

20. No Correlation

21. Slope Measures the steepness of the data. Equidistant the data slope shows the correlation is good and greater the importance of the relationship.

22. Strong Correlation

23. Moderate Correlation

24. No Correlation

25. Direction The "X" variable can have a positive or a negative impact on the "Y" variable. In positive correlation both the values increases together. In negative correlation both the values decreases together.

26. Positive Correlation

27. Negative Correlation

28. Banana Shaped Correlation

29. Boomerang Shaped Correlation

30. Summary Scatter Plot is a Quality Tool used to analyze numeric data. Used to identify correlation between the causes and effects and to understand their correlation. Helpful to control the effects in the desired manner after identifying the kind of correlation. Useful for Cause and Effect Analysis.

31. Thank You…