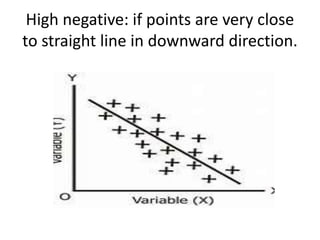
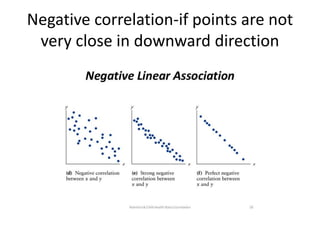
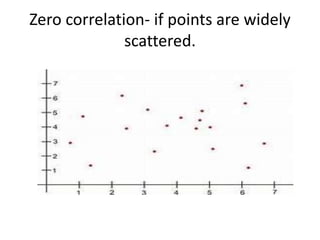
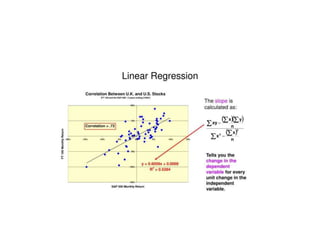
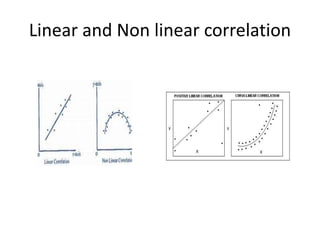
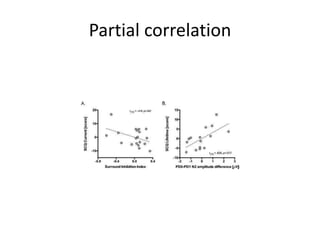
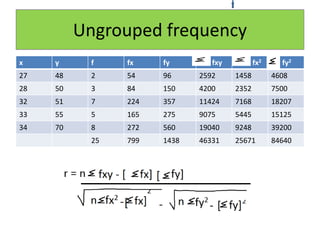
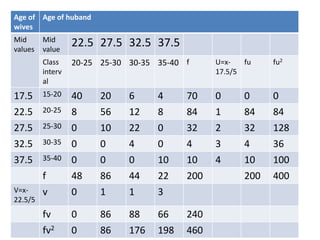
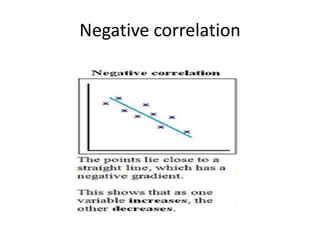
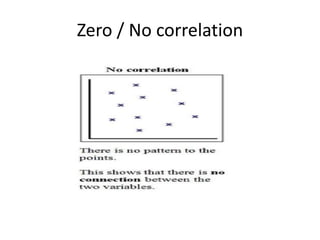
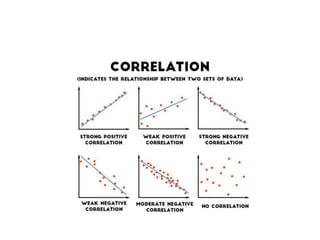
Correlation analysis

Correlation
• If two variable are so inter-related in such a
manner that change in one variable brings about
in other variable, then this type of relation of
variable known as correlation.
• If we change the value of one variable that will
make corresponding change in the value of other
variable on average then we can say two
variables are correlation.
• The value of correlation coefficient will vary from
-1 to +1.

Types of correlation
• Positive , negative and zero
correlation
• Linear and non linear correlation
• Simple, partial and multiple
correlation.

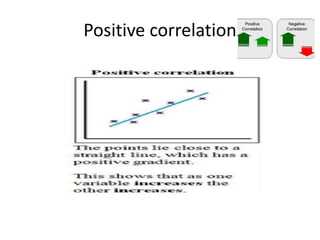
All points in correlation. The straight
line in upward direction [ left bottom
to right up]

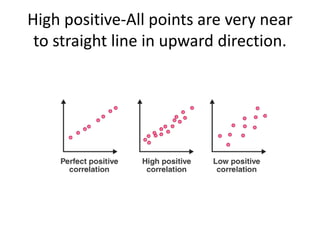
High positive-All points are very near
to straight line in upward direction.

Positive correlation-all points are near
to the straight line [ but not very near ]
correlation is positive.

Perfect negative-if all the points in a
scattered diagram lies in a straight line
in downward direction [ left to right
bottom.

High negative: if points are very close
to straight line in downward direction.

Negative correlation-if points are not
very close in downward direction

Zero correlation- if points are widely
scattered.

Linear and Non linear correlation

Bivariate data
• Bivariate data is concerned with
examining the relationship between two
variables.
• If two or more quantities vary in
sympathy so that the movements in one
tend to be accompanied by
corresponding movements in the other.

Positive and negative correlation
It is said to be positive , when
the variables move in the same
direction and negative when
they move in opposite.

uncorrelated
If the movement of one
variables does not effect
that of the other, the
variables are said to be
uncorrelated.

Correlation may be linear or non
linear.
If the amount of variation in x
bears a constant ratio to the
corresponding amount of variation
in y then the correlation between x
and y is said to be linear. Otherwise
it is non linear.

• The degree of a linear relationship between
two variables is measured by the karl
pearson’s coefficient of correlation or
correlation coefficient ‘r’.
• Correlation is meaningful when both the
variables x and y are the measured outcomes.
• If one variable is controlled by the researcher,
linear regression ought to be used instead of
correlation.
Pearson correlation coefficient

• Correlation analysis do not differentiate
between two variables but quantify the
relationship between them.
• Regression is to be chosen instead of
correlation if the variables x and y are clearly
defined.

• It is a measure of the linear relationship
between two attributes or column of data ‘r’.
• The non parametric spearman correlation
coefficient is rho ranges from +1 to -1
• If r and rho is far from zero. There are four
possible explanation.

Properties of pearson’s correlation
coefficient
• The value of r is dimensionless and can range
from -1 to +1 and is independent of the units
of measurement.
• Therefore the coefficient can be used to
compare different set of data.
• Pearson’s correlation coefficient is
independent of change of origin and scale.

Significance of Pearson’s correlation
coefficient
If r= 1 the x and y are positively correlated.
• The possible values of x and y all lie on a straight
line with a positive slope in the x,y plane.
• Example of perfect positive correlation are rare in
biological and social sciences.
• One example of perfect positive correlation is
charle’s law. When the volume of a gas is
constant , its pressure is directly proportional to
the temperature.

• If o < r then x and y have positive
correlation.
• Eg. It include age of husband and
wife ; educational level and age at
marriage ; and height and weight of
children.
coefficient

If r=0 then x and y are not
correlated. They do not have
apparent linear relationship.
However this does not mean that x
and y are statistically independent.
coefficient

If r < -1 then x and y have strong
negative correlation. Example of
negative correlation include infant
mortality rate and level of mothers
education; and fertility rates and
education level.
coefficient

• If r= -1 then x snd y are perfectly negatively
correlated.
• The possible values of x and y all lie in a
straight line with a negative slope in the x1y1
plane.
• Perfect negative slope in biological science is
rare one example is Boyle’s law . when the
temperature is kept constant pressure of gas is
inversely proportional to its volume.
coefficient

For large sample standard error of
correlation is determined using the
formula

For small sample the significance is
determined using t test.
The t value can range between minus
infinity and plus infinity.
The t value near 0 is evidence for the null
hypothesis that there is no correlation
between the attribute

Procedure for interpretation of
data/result
• Determine how the variables x and y vary
together.
• Consider the value of r or rho which quantifies
the correlation
• Consider the rho value
• Consider the confidence interval for ‘r’

• If P value is small correlation is not due to
mere coincidence, the true population ‘r’ lies
within the confidence interval.
• If p value is large , it means that there is no
compelling evidence that the correlation is
real and not a coincidence.

Method of correlation analysis
• Bivariate two way frequency table
It is the simplest method of obtaining
correlation between two variables but since it
only gives a rough estimate of the degree of
correlation. If it is not generally used.
• Scatter diagram
• Karl Pearson’s method
• Rank method

Karl pearson’s method
• It can be calculated for simple data,
ungrouped and grouped frequency.
• For simple data

The haemoglobin level and plasma
volume of 10 person calculate the
correlation coefficient between
haemoglobin and plasma volume
Pearson
number
1 2 3 4 5 6 7 8 9 10
Hb x 13 13.4 13.5 13.9 15.5 14.5 15 15.2 15.6 14.2
Plasma
volume
y
44 45 46 47 47 49 50 51 52 49

Ungrouped frequency
x y f fx fy fxy f fx2 fy2
27 48 2 54 96 2592 1458 4608
28 50 3 84 150 4200 2352 7500
32 51 7 224 357 11424 7168 18207
33 55 5 165 275 9075 5445 15125
34 70 8 272 560 19040 9248 39200
25 799 1438 46331 25671 84640

Age of
wives
Age of huband
Mid
values
Mid
value
22.5 27.5 32.5 37.5
Class
interv
al
20-25 25-30 30-35 35-40 f U=x-
17.5/5
fu fu2
17.5 15-20 40 20 6 4 70 0 0 0
22.5 20-25 8 56 12 8 84 1 84 84
27.5 25-30 0 10 22 0 32 2 32 128
32.5 30-35 0 0 4 0 4 3 4 36
37.5 35-40 0 0 0 10 10 4 10 100
f 48 86 44 22 200 200 400
V=x-
22.5/5
v 0 1 1 3
fv 0 86 88 66 240
fv2 0 86 176 198 460

Multiple correlation analysis
• It involves 3 or more variables
• Dependent variables are denoted by x1,x2,x3..
• X1= weight in lbs
• X2= height in inches
• X3= age in years
• The coefficient of multiple linear correlation is
represented by R1.
• The coefficient of multiple correlation lies
between 0 and 1.

• If r is closer to 1 better is the linear relationship
between the variable.
• If r is closer to 0 the worse is linear relationship.
• If the coefficient of multiple correlation is 1 then
the correlation is perfect.
• If r=0 then there is a possibility non linear
relationship between the variables.
• Multiple correlation coefficient is always positive
in sign range from +1 to 0

Advantage
• It serve as a measure of the degree of association
between one variable taken as the dependent
variable and a group of other variables taken as
the independent variables.
• It also serve as a measure of goodness of fit of
the calculated plane of regression and
consequently as a measure of the general degree
of accuracy of estimates made by reference to
equation for the plane of regression.

Limitation
• It is based on assumption that the relationship
between the variables is linear.
• It requires much skill for calculation.
• Lack of understanding and resulting misuse
are due to the complexity of the method.
• In practice most relationships are not linear
but follow some pattern. This limits somewhat
the use of multiple correlation analysis

Correlation analysis

More Related Content

What's hot

Similar to Correlation analysis

More from gopinathannsriramachandraeduin

Recently uploaded

Correlation analysis