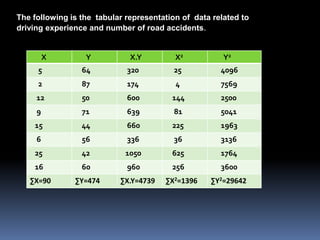
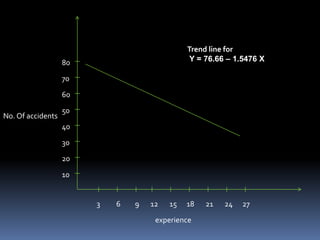
The document presents a regression analysis on the relationship between driving experience (the independent variable X) and the number of road accidents (the dependent variable Y). It finds the regression line to be Y = 76.66 - 1.5476X, indicating a negative relationship between accidents and experience. Using this line, it estimates the number of accidents would be 61.184 for 10 years experience and 30.232 for 30 years experience. It also calculates the coefficient of determination R2 = 0.5894, meaning driving experience explains around 59% of the variance in road accidents.

1. BUSINESS STATISTICS
PRESENTATION
ON
REGRESSION ANALYSIS
PRESENTED BY-HARI
BHATTARAI
MBA 1STYEAR

2. OBJECTIVES OF THE PRESENTATION-
What is regression analysis
Types and methods of regression analysis
Practical aspect of regression analysis with an
example

3. INTRODUCTION-
Regression analysis is the statistical tool which is
employed for the purpose of forecasting or making
estimates
 Here we make use of various mathematical formulas
and assumptions to describe a real world situation.
 In every situation, estimation becomes easy once it is
known that the variable to be estimated is related to and
dependent to some other variable.

4. For making estimates we first have to model the relationship
between the variable involved .
Models can me broadly be classified into –
Linear regression-
 Linear regression analysis is a powerful technique used for
predicting the unknown value of a variable from the known
value of another variable.
More precisely, if X and Y are two related variables, then
linear regression analysis helps us to predict the value of Y
for a given value of X or vice verse.
For example age of a human being and maturity are related
variables. Then linear regression analyses can predict level
of maturity given age of a human being.

5. Multiple regression-
 Multiple regression analysis is a powerful technique
used for predicting the unknown value of a variable from
the known value of two or more variables- also called the
predictors.
Multiple regression analysis helps us to predict the value
of Y for given values of X1, X2, …, Xk.
For example the yield of rice per acre depends upon
quality of seed, fertility of soil, fertilizer used, temperature,
rainfall. If one is interested to study the joint affect of all
these variables on rice yield, one can use this technique.

6. Dependent and Independent Variables-
 By linear regression, we mean models with just one
independent and one dependent variable. The variable whose
value is to be predicted is known as the dependent variable
and the one whose known value is used for prediction is
known as the independent variable.
 By multiple regression, we mean models with just one
dependent and two or more independent variables. The
variable whose value is to be predicted is known as the
dependent variable and the ones whose known values are
used for prediction are known independent variables.

7. Methods of solving regression models-
1) GRAPHICAL METHOD-In
this graphical method the average relationship
between the dependent variable and independent
variable is expressed by a line called “line of best fit”.
Example: Experience( in years) Income( in ‘000)
15 150
10 120
5 60
3 40
8 70
9 90

8. 2 4 6 8 10 12 14 16
210
180
150
120
90
60
30
18
240
0
Line of best fit
income
experience

9. 2) ALGEBRIC METHOD-In
this method we make use of regression equation
and regression coefficients.
Regression equation(Linear).
A statistical technique used to explain or predict thebehaviour of a dependent
variable
The general equation is given by- y = a + bx a is the intercept
b is the slope of line
With the use of the above general equation we find the normal equations
Multiplying the general equation by N and taking the summatation of it
we find the first normal equation i.e.
ΣY = N.a + bΣX
And again to find the second normal equation we multiply the general
equation by x and then take the summatation i.e.
ΣXY=a ΣX + b ΣX2

10. Regression equation(Multiple).
General equation => y = a + b1 x1 + b2x2 + .........+ bnxn
Normal equations for multiple regression are:
ΣY = N.a + b1ΣX1 + b2ΣX2
ΣX1Y= a ΣX1 + b1 Σ X1
2 + b2Σ X1 . X2
2
ΣX2Y= a ΣX2 + b1 Σ X1 . X2 + b2Σ X2

11. Lines of Regression
There are two lines of regression- that of Y on X and X on Y.
The line of regression of Y on X is given by Y = a + bX where a and b
are unknown constants known as intercept and slope of the equation.
This is used to predict the unknown value of variable Y when value of
variable X is known.
On the other hand, the line of regression of X on Y is given by X = c + dY
which is used to predict the unknown value of variable X using the
known value of variable Y.
Often, only one of these lines make sense.
Exactly which of these will be appropriate for the analysis in hand will
depend on labeling of dependent and independent variable in the
problem to be analyzed.

12. Regression coefficients-
The coefficient of X in the line of regression of Y on X is called the
regression coefficient of Y on X and is denoted by b y x
It represents change in the value of dependent variable (Y)corresponding to
unit change in the value of independent variable (X).
And similarly the coefficient of Y in the line of regression of X on Y is
called coefficient of X on Y and is denoted by b x y .
The two regression co-efficient are byx and bxy .
The formula for the two regression co- efficient are given by –
or b y x = N .ΣXY − Σ X . ΣY
N. ΣX2 − (ΣX)2
b x y = N.Σ XY – ΣX . ΣY
N. ΣY2 – (ΣY)2

13. How Good Is the Regression?
Once a regression equation has been constructed, we can
check how good it by examining the coefficient of
determination (R2).
R2 always lies between 0 and 1.
The closer R2 is to 1, the better is the model and its
prediction.

14. PRACTICAL ASPECT OF REGRESSION ANALYSIS-
Here we will show a linear regression analysis between two
variables X and Y.
 Variable X is taken as “ driving experience” and variable Y is
taken as “number of road accidents(in a year)”.
 Road accident is taken as the dependent variable and which
is related to independent variable X i.e. driving experience.
X (driving
experience)
5 2 12 9 15 6 25 16
Y ( no. of
road
accidents)
64 87 50 71 44 56 42 60

15. From the date we will show-
 The estimated regression line for the date.
 Number of road accidents taking place when the
driving experience is 10 years and 30 years.
 co efficient of determination(R2) and which will
help us to know that how much percentage of
dependent variable is explained by independent
variable.

16. The following is the tabular representation of data related to
driving experience and number of road accidents.
X Y X.Y X2 Y2
5 64 320 25 4096
2 87 174 4 7569
12 50 600 144 2500
9 71 639 81 5041
15 44 660 225 1963
6 56 336 36 3136
25 42 1050 625 1764
16 60 960 256 3600
ΣX=90 ΣY=474 ΣX.Y=4739 ΣX2=1396 ΣY2=29642

17. Since the estimated regression line is given by Y = a + b.X , now
using the normal equations we calculate the value of a and b .
ΣY = N. a + b ΣX
474= 8.a + b.90
8a + 90b = 474 E .q - 1
ΣXY=a ΣX + b ΣX2
4739 = a.90 + b.1396
90a + 1396 b = 4739 E.q-2
Now solving both the equation we get the value of a and b as-
Value of a = 76.66
Value of b = -1.5475
The estimated regression line is
Y = 76.66 – 1.5476 X

18. 3 6 9 12 15 18 21 24 27
experience
80
70
60
50
40
30
20
10
No. Of accidents
Trend line for
Y = 76.66 – 1.5476 X

19. Since we all know that the road accidents are dependent upon the driving
experience and a new driver is considered to be inexperienced and for
him the risk of accident is more so there exist a negative relationship
between the two variables so the trend line is downward sloping in this
case.
From the above value of a and b we can see that value of a is 76.66 which
means if a driver has 0 experience then the no of road accidents that will
take place is 76.66
From the value of b we can say that for every extra year of driving
experience , the road accident is decreased by 1.5476
No of accidents with 10 yr experience No. of accidents with 30 yr experience
Y = 76.66 – 1.5476 X
Y = 76.66 – 1.5476 (10)
Y = 61. 184
Y = 76.66 – 1.5476 X
Y = 76.66 – 1.5476 (30)
Y= 30.232

20. Now we find coefficient of variation for the data
using regression coefficients.
b y x = N .ΣXY − Σ X . ΣY
N. ΣX2 − (ΣX)2
b x y = N.Σ XY – ΣX . ΣY
N. ΣY2 – (ΣY)2
= 8 (4739) − 90 . 474
8(1396) − (90)2
= − 1.547
= 8(4739) − 90. 474
8(29642)− (474)2
= − 0.381
Now R2 = b y x .b x y
= (- 1. 547) (- 0.381)
= 0.5894
From the above coefficient of determination we can say that almost 59 %
of variance of dependent variable is explained by the independent
variable.